4.2: Uhamisho na Vectors Velocity

Last updated
Save as PDF

Page ID: 176978

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

MALENGO YA KUJIFUNZA

Tumia vectors msimamo katika tatizo multidimensional makazi yao.
Tatua kwa uhamisho katika vipimo viwili au vitatu.
Tumia vector kasi kutokana na vector msimamo kama kazi ya muda.
Tumia kasi ya wastani katika vipimo vingi.

Uhamisho na kasi katika vipimo viwili au vitatu ni upanuzi wa moja kwa moja wa ufafanuzi wa mwelekeo mmoja. Hata hivyo, sasa ni kiasi cha vector, hivyo mahesabu pamoja nao wanapaswa kufuata sheria za algebra ya vector, sio algebra ya scalar.

makazi yao vector

Kuelezea mwendo katika vipimo viwili na vitatu, lazima kwanza kuanzisha mfumo wa kuratibu na mkataba wa axes. Sisi kwa ujumla kutumia kuratibu$x$,$y$, na$z$ Machapisho chembe$P(x, y, z)$ katika hatua katika vipimo tatu. Kama chembe ni kusonga$x$, vigezo$y$, na$z$ ni kazi ya muda ($t$):

\[x = x(t) \quad y = y(t) \quad z = z(t) \ldotp \label{4.1}\]

Vector msimamo kutoka asili ya mfumo wa kuratibu kwa uhakika P ni$\vec{r}(t)$. Katika kitengo vector nukuu, kuletwa katika Kuratibu Systems na Vipengele ya Vector,$\vec{r}$ (t) ni

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k} \ldotp \label{4.2}\]

Kielelezo$\PageIndex{1}$ kinaonyesha mfumo wa kuratibu na vector kwa uhakika$P$, ambapo chembe inaweza kuwa iko kwa wakati fulani$t$. Kumbuka mwelekeo wa x, y, na z axes. Mwelekeo huu unaitwa mfumo wa kuratibu wa kulia na hutumiwa katika sura.

Mfumo wa kuratibu x y z unaonyeshwa, na x chanya nje ya ukurasa, y chanya kwa haki, na chanya z up. Hatua P, na kuratibu x ya t, y ya t, na z ya t inavyoonyeshwa. Kuratibu zote za P ni chanya. Vector r ya t kutoka asili kwa P pia inavyoonekana kama mshale wa zambarau. Kuratibu x ya t, y ya t na z ya t huonyeshwa kama mistari iliyopigwa. X ya t ni sehemu katika ndege x y, sambamba na mhimili x, y ya t ni sehemu katika ndege x y, sambamba na mhimili y, na z ya t ni sehemu inayofanana na mhimili wa z. — Kielelezo$\PageIndex{1}$: mfumo wa kuratibu tatu-dimensional na chembe katika nafasi$P(x(t), y(t), z(t))$.

Kwa ufafanuzi wetu wa nafasi ya chembe katika nafasi tatu-dimensional, tunaweza kuunda makazi ya tatu-dimensional. Kielelezo$\PageIndex{3}$ kinaonyesha chembe wakati t ₁ iko katika P ₁ na vector nafasi$\vec{r}$ (t ₁). Wakati mwingine t ₂, chembe iko katika P ₂ na vector nafasi$\vec{r}$ (t ₂). Vector$\Delta \vec{r}$ ya uhamisho hupatikana kwa kuondoa$\vec{r}(t_1)$ kutoka$\vec{r}(t_2)$:

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) \ldotp \label{4.3}\]

Vector Aidha ni kujadiliwa katika Vectors. Kumbuka kuwa hii ni operesheni sawa tuliyofanya kwa mwelekeo mmoja, lakini sasa vectors ni katika nafasi tatu-dimensional.

Mfumo wa kuratibu x y z unaonyeshwa, na x chanya nje ya ukurasa, y chanya kwa haki, na chanya z up. Pointi mbili, P 1 na P 2 zinaonyeshwa. Vector r ya t 1 kutoka asili hadi P 1 na vector r ya t 2 kutoka asili hadi P 2 huonyeshwa kama mishale ya zambarau. Vector delta r inavyoonekana kama mshale wa zambarau ambao mkia wake ni P 1 na kichwa katika P 2. — Kielelezo$\PageIndex{2}$: makazi yao$\Delta \vec{r} = \vec{r}(t_2) − \vec{r}(t_1)$ ni vector kutoka$P_1$ kwa$P_2$.

Mifano zifuatazo zinaonyesha dhana ya kuhama kwa vipimo vingi

Mfano 4.1: Satellite ya Polar inayozunguka

Satellite iko katika obiti ya mviringo ya polar karibu na Dunia katika urefu wa 400 km—maana, inapita moja kwa moja juu katika Poles Kaskazini na Kusini. Je, ni ukubwa na mwelekeo wa vector ya uhamisho kutoka wakati ni moja kwa moja juu ya Ncha ya Kaskazini hadi wakati iko kwenye latitude -45°?

Mkakati

Tunafanya picha ya tatizo ili kutazama suluhisho graphically. Hii itasaidia katika ufahamu wetu wa uhamisho. Sisi kisha kutumia kitengo wadudu kutatua kwa ajili ya makazi yao.

Suluhisho

Kielelezo$\PageIndex{3}$ kinaonyesha uso wa Dunia na mduara unaowakilisha obiti ya satellite. Ingawa satelaiti zinahamia katika nafasi tatu-dimensional, zinafuata trajectories ya ellipses, ambayo inaweza kupigwa kwa vipimo viwili. Vectors msimamo hutolewa kutoka katikati ya Dunia, ambayo tunachukua kuwa asili ya mfumo wa kuratibu, na y axis kama kaskazini na x-axis kama mashariki. Vector kati yao ni uhamisho wa satellite. Tunachukua radius ya Dunia kama kilomita 6370, hivyo urefu wa kila vector nafasi ni 6770 km.

Mfumo wa kuratibu x y, unaozingatia duniani, unaonyeshwa. Chanya x ni upande wa mashariki na chanya y kaskazini. Mduara wa bluu mkubwa kuliko na unaozingatia dunia unaonyeshwa. Vector r ya t 1 ni mshale wa machungwa kutoka asili hadi mahali ambapo mduara wa bluu unavuka mhimili y (digrii 90 za kukabiliana na saa moja kwa moja kutoka kwa mhimili x mzuri.) Vector r ya t 2 ni mshale wa machungwa kutoka asili hadi mahali kwenye mduara wa bluu chini ya digrii 45. Delta r vector ni umeonyesha kama zambarau mshale akizungumzia chini na kulia, kuanzia kichwa cha vector r ya t 1 na kuishia katika kichwa cha vector r ya t 2. — Kielelezo$\PageIndex{3}$: Vectors mbili za msimamo hutolewa kutoka katikati ya Dunia, ambayo ni asili ya mfumo wa kuratibu, na y axis kama kaskazini na x-axis kama mashariki. Vector kati yao ni uhamisho wa satellite.

Katika kitengo vector nukuu, wadudu nafasi ni

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \; km\; \hat{j} \\[4pt] \vec{r}(t_{2}) &= 6770 \ldotp \; km (\cos (-45°))\; \hat{i} + 6770 \ldotp \; km (\sin(−45°))\; \hat{j} \ldotp \end{align*}\]

Kutathmini sine na cosine, tuna

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \hat{j} \\[4pt] \vec{r}(t_{2}) &= 4787\; \hat{i} − 4787\; \hat{j} \ldotp \end{align*}\]

Sasa tunaweza kupata$\Delta \vec{r}$, makazi yao ya satellite:

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) = 4787\; \hat{i} - 11,557\; \hat{j} \ldotp \nonumber\]

Ukubwa wa makazi yao ni

\[|\Delta \vec{r}| = \sqrt{(4787)^{2} + (-11,557)^{2}} = 12,509\; km. \nonumber\]

Pembe ya uhamisho hufanya na x-axis ni

\[\theta = \tan^{-1} \left(\dfrac{-11,557}{4787}\right) = -67.5^{o} \nonumber.\]

Umuhimu

Kupanga uhamisho hutoa habari na maana kwa suluhisho la vector kitengo kwa tatizo. Wakati wa kupanga njama, tunahitaji kuingiza vipengele vyake pamoja na ukubwa wake na angle inafanya na mhimili uliochaguliwa - katika kesi hii, x-axis (Kielelezo$\PageIndex{4}$).

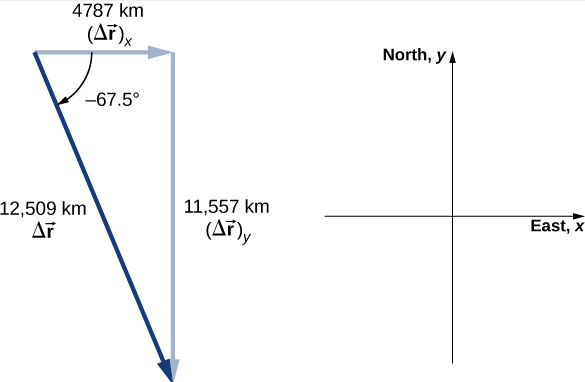
Mfumo wa kuratibu x y unaonyeshwa. Chanya x ni upande wa mashariki na chanya y kaskazini. Vector delta r ndogo x anasema mashariki na ina ukubwa 4787 kilomita. Vector delta r ndogo y anasema kusini na ina ukubwa 11,557 kilomita. Vector delta r pointi kusini, kuanzia saa mkia wa delta r ndogo x na kuishia katika kichwa cha delta r ndogo y na ina ukubwa 12,509 kilomita. — Kielelezo$\PageIndex{4}$: Vector ya uhamisho na vipengele, angle, na ukubwa.

Kumbuka kuwa satellite ilichukua njia ya pembe kwenye obiti yake ya mviringo ili kupata kutoka nafasi yake ya awali hadi nafasi yake ya mwisho katika mfano huu. Pia ingeweza kusafiri kilomita 4787 mashariki, halafu km 11,557 kusini kufika katika eneo moja. Njia hizi zote mbili ni ndefu kuliko urefu wa vector ya uhamisho. Kwa kweli, vector ya uhamisho hutoa njia fupi kati ya pointi mbili kwa vipimo moja, mbili, au tatu.

Maombi mengi katika fizikia yanaweza kuwa na mfululizo wa uhamisho, kama ilivyojadiliwa katika sura iliyopita. Uhamisho wa jumla ni jumla ya uhamisho wa mtu binafsi, wakati huu tu, tunahitaji kuwa makini, kwa sababu tunaongeza vectors. Tunaonyesha dhana hii kwa mfano wa mwendo wa Brownian.

Mfano 4.2: Mwendo wa Brownian

Mwendo wa Brownian ni mwendo wa random wa machafuko wa chembe zilizosimamishwa katika maji, kutokana na migongano na molekuli ya maji. Mwendo huu ni wa tatu. Kuhamishwa kwa utaratibu wa namba ya chembe inayoendelea mwendo wa Brownian inaweza kuonekana kama yafuatayo, katika micrometers (Kielelezo$\PageIndex{5}$):

\[\Delta \vec{r}_{1} = 2.0\; \hat{i} + \hat{j} + 3.0 \hat{k}\]

\[\Delta \vec{r}_{2} = - \hat{i} + 3.0\; \hat{k}\]

\[\Delta \vec{r}_{3} = 4.0\; \hat{i} -2.0\; \hat{j} + \hat{k}\]

\[\Delta \vec{r}_{4} = -3.0\; \hat{i} + \hat{j} + 3.0\; \hat{k} \ldotp\]

Je, ni uhamisho wa jumla wa chembe kutoka kwa asili?

Mfumo wa kuratibu x y z na umbali uliopimwa katika micrometers na kuanzia -10 hadi +10 micrometers inavyoonyeshwa. makazi yao delta r ndogo 1 sawa 2 I kofia pamoja j kofia pamoja 2 k kofia, delta r ndogo 2 sawa -1 I kofia pamoja 3 k kofia, na delta r ndogo 3 sawa -3 I kofia pamoja na j kofia pamoja 2 k kofia ni umeonyesha kama bluu line makundi. Vector r 1 kofia huanza katika asili. Kila uhamisho unaofuata huanza ambapo uliopita umekoma. Vector delta r jumla inavyoonekana kama mstari nyekundu kuanzia saa asili na kuishia mwishoni mwa vector delta r 4. Delta r jumla sawa 2 I kofia pamoja 0 y kofia pamoja 9 k kofia. — Kielelezo$\PageIndex{5}$: Trajectory ya chembe kufanyiwa makazi yao random ya mwendo Brownian. Uhamisho wa jumla unaonyeshwa kwa nyekundu.

Suluhisho

Tunaunda jumla ya uhamisho na kuwaongeza kama vectors:

\[\begin{split} \Delta \vec{r}_{Total} & = \sum \Delta \vec{r}_{i} = \Delta \vec{r}_{1} + \Delta \vec{r}_{2} + \Delta \vec{r}_{3} + \Delta \vec{r}_{4} \\ & = (2.0 - 1.0 + 4.0 - 3.0)\; \hat{i} + (1.0 + 0 - 2.0 + 1.0)\; \hat{j} + (3.0 +3.0 + 1.0 + 2.0)\; \hat{k} \\ & = 2.0\; \hat{i} + 0\; \hat{j} + 9.0\; \hat{k}\; \mu m \ldotp \end{split}\]

Ili kukamilisha suluhisho, tunaelezea uhamisho kama ukubwa na mwelekeo,

\[| \Delta \vec{r}_{Total}| = \sqrt{2.0^{2} + 0^{2} + 9.0^{2}} = 9.2 \mu m, \quad \theta = \tan^{-1} \left(\dfrac{9}{2}\right) = 77^{o},\]

kwa heshima ya x-axis katika ndege ya xz.

Umuhimu

Kutoka kwa takwimu tunaweza kuona ukubwa wa makazi ya jumla ni chini ya jumla ya ukubwa wa uhamisho wa mtu binafsi.

Vector kasi

Katika sura iliyotangulia tulipata kasi ya papo hapo kwa kuhesabu derivative ya kazi ya msimamo kwa heshima na wakati. Tunaweza kufanya operesheni sawa katika vipimo viwili na vitatu, lakini tunatumia vectors. Vector kasi instantaneous ni sasa

\[\vec{v} (t) = \lim_{\Delta t \rightarrow 0} \frac{\vec{r} (t + \Delta t) - \vec{r} (t)}{\Delta t} = \frac{d \vec{r}}{dt} \ldotp \label{4.4}\]

Hebu tuangalie mwelekeo wa jamaa wa vector nafasi na vector kasi graphically. Katika Kielelezo$\PageIndex{6}$ tunaonyesha vectors$\vec{r}$ (t) na$\vec{r}$ (t +$\Delta$ t), ambayo hutoa nafasi ya chembe inayohamia njia inayowakilishwa na mstari wa kijivu. Kama$\Delta$ t inakwenda sifuri, vector ya kasi, iliyotolewa na Equation\ ref {4.4}, inakuwa tangent kwa njia ya chembe wakati t.

Vectors r ya t na r ya t plus delta t huonyeshwa kama mishale nyekundu katika mfumo x y kuratibu. Wote vectors kuanza katika asili. Vector delta r anasema kutoka kichwa cha vector r ya t kwa kichwa cha vector r ya t plus delta t. — Kielelezo$\PageIndex{6}$: Chembe huenda kando ya njia iliyotolewa na mstari wa kijivu. Katika kikomo kama$\Delta$ t inakaribia sifuri, vector ya kasi inakuwa tangent kwa njia ya chembe.

Equation\ ref {4.4} pia inaweza kuandikwa kwa suala la vipengele vya$\vec{v}$ (t). Tangu

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k},\]

tunaweza kuandika

\[\vec{v} (t) = v_{x} (t)\; \hat{i} + v_{y} (t)\; \hat{j} + v_{z} (t)\; \hat{k} \label{4.5}\]

wapi

\[v_{x} (t) = \frac{dx(t)}{dt}, \quad v_{y} (t) = \frac{dy(t)}{dt}, \quad v_{z} (t) = \frac{dz(t)}{dt} \ldotp \label{4.6}\]

Ikiwa tu kasi ya wastani ni ya wasiwasi, tuna vector sawa na kasi moja ya mwelekeo wa wastani kwa vipimo viwili na vitatu:

\[\vec{v}_{avg} = \frac{\vec{r} (t_{2}) - \vec{r} (t_{1})}{t_{2} - t_{1}} \ldotp \label{4.7}\]

Mfano 4.3: Kuhesabu Vector Velocity

Kazi ya msimamo wa chembe ni$\vec{r}$ (t) = 2.0t ²$\hat{i}$ + (2.0$\hat{j}$ + 3.0t) + 5.0t$\hat{k}$ m. (a) Ni kasi gani na kasi ya t = 2.0 s? (b) Kasi ya wastani kati ya 1.0 s na 3.0 s ni nini?

Suluhisho

Kutumia Equation\ ref {4.5} na Equation\ ref {4.6}, na kuchukua derivative ya kazi ya nafasi kwa heshima na wakati, tunapata

$v (t) =\ frac {d\ vec {r} (t)} {dt} = 4.0t\;\ kofia {i} + 3.0\;\ kofia {j} + 5.0\;\ kofia {k}\; m/s $$$\ vec {v} (2.0\; s) = 8.0\;\ kofia {i} + 3.0\;\ kofia {j} + 5.0\;\ kofia {k}\; m/s $$$kasi\; |\ vec {v} (2.0\; s) | =\ sqrt {8^ {2} + 3^ {2} + 5^ {2}} = 9.9\; m/s\ ldotp$$
Kutoka Equation\ ref {4.7}, $$\ kuanza {split}\ vec {v} _ {avg} & =\ frac {\ vec {r} (t_ {2}) -\ vec {r} (t_ {1})} {t_ {2} - t_ {1}} =\ frac {\ vec {r} (3.0\ s) -\ vec {r} (1.0\; s)} {3.0\; s - 1.0\; s} =\ frac {(18\;\ kofia {i} + 11\;\ kofia {j} + 15\;\ kofia {k}) m - (2\;\ kofia {i} + 5\;\ kofia {j} + 5\;\ kofia {k}) m} {2.0\; s}\ & =\ frac {( 16\;\ kofia {i} + 6\;\ kofia {j} + 10\;\ kofia {k}) m} {2.0\; s} = 8.0\;\ kofia {i} + 3.0\;\ kofia {j} + 5.0\;\ kofia {k}\; m/s\ ldotp\ mwisho {mgawanyiko} $$

Umuhimu

Tunaona kasi ya wastani ni sawa na kasi ya instantaneous saa t = 2.0 s, kama matokeo ya kazi ya kasi kuwa linear. Hii haipaswi kuwa kesi kwa ujumla. Kwa kweli, wakati mwingi, kasi ya haraka na ya wastani si sawa.

Zoezi 4.1

Kazi ya msimamo wa chembe ni$\vec{r}$ (t) = 3.0t ³$\hat{i}$ + 4.0$\hat{j}$. (a) Kasi ya papo hapo ni nini katika t = 3 s? (b) Je, kasi ya wastani kati ya 2 s na 4 s sawa na kasi ya instantaneous saa t = 3 s?

Uhuru wa Mwendo wa Perpendicular

Tunapoangalia equations tatu-dimensional kwa nafasi na kasi iliyoandikwa katika kitengo vector nukuu, Equation\ ref {4.2} na Equation\ ref {4.5}, tunaona vipengele vya equations hizi ni tofauti na kazi za kipekee za muda ambazo hazitegemeani. Mwendo kando ya mwelekeo wa x hauna sehemu ya mwendo wake pamoja na maelekezo ya y na z, na vilevile kwa axes nyingine mbili za kuratibu. Kwa hiyo, mwendo wa kitu katika vipimo viwili au vitatu vinaweza kugawanywa katika mwendo tofauti, wa kujitegemea pamoja na pembe za perpendicular za mfumo wa kuratibu ambapo mwendo unafanyika.

Ili kuonyesha dhana hii kwa heshima ya uhamisho, fikiria mwanamke anatembea kutoka hatua A hadi kumweka B katika mji wenye vitalu vya mraba. Mwanamke anayechukua njia kutoka A hadi B anaweza kutembea mashariki kwa vitalu vingi na kisha kaskazini (pande mbili za perpendicular) kwa seti nyingine ya vitalu kufika B. umbali gani anatembea mashariki huathirika tu na mwendo wake upande wa mashariki. Vilevile, umbali gani anatembea kaskazini anaathiriwa tu na mwendo wake kuelekea kaskazini.

Uhuru wa Mwendo

Katika maelezo ya kinematic ya mwendo, tunaweza kutibu vipengele vya usawa na wima vya mwendo tofauti. Mara nyingi, mwendo katika mwelekeo usio na usawa hauathiri mwendo katika mwelekeo wa wima, na kinyume chake.

Mfano unaoonyesha uhuru wa mwendo wa wima na usawa hutolewa na baseballs mbili. Baseball moja imeshuka kutoka kupumzika. Wakati huo huo, mwingine huponywa kwa usawa kutoka urefu sawa na inafuata njia iliyopigwa. Stroboscope inachukua nafasi za mipira kwa vipindi vya muda vilivyowekwa wakati wanapoanguka (Kielelezo$\PageIndex{7}$).

Mipira miwili inayofanana inaonyeshwa kwenye maeneo 5 kwa vipindi sawa vya wakati. Mipira huanza kwenye nafasi sawa ya wima. Mishale ya kijani inawakilisha kasi ya usawa na mishale ya zambarau inawakilisha kasi ya wima katika kila nafasi. Mpira upande wa kulia una kasi ya awali ya usawa ambapo mpira upande wa kushoto hauna kasi ya usawa. Mwendo wa usawa ni kasi ya usawa wa mara kwa mara wakati wote kwa mipira yote. Mwendo wa wima ni kuongeza kasi ya wima mara kwa mara. Kila mpira wima kasi ni kuongezeka kwa ukubwa na akizungumzia chini. Kwa kila papo kwa wakati, mipira yote ina nafasi za wima sawa na kasi za wima. — Kielelezo$\PageIndex{7}$: Mchoro wa mwendo wa mipira miwili inayofanana: moja huanguka kutoka kupumzika na nyingine ina kasi ya awali ya usawa. Kila msimamo unaofuata ni muda sawa wa wakati. Mishale inawakilisha kasi ya usawa na wima katika kila nafasi. Mpira upande wa kulia una kasi ya awali ya usawa ambapo mpira upande wa kushoto hauna kasi ya usawa. Licha ya tofauti katika kasi ya usawa, kasi za wima na nafasi zinafanana kwa mipira yote, ambayo inaonyesha mwendo wa wima na usawa ni huru.

Ni ajabu kwamba kwa kila flash ya strobe, nafasi za wima za mipira miwili ni sawa. Ufanana huu unamaanisha mwendo wa wima ni huru kama mpira unahamia kwa usawa. (Kutokana hakuna upinzani wa hewa, mwendo wa wima wa kitu cha kuanguka huathiriwa na mvuto tu, si kwa nguvu yoyote ya usawa.) Uchunguzi wa makini wa mpira uliotupwa kwa usawa unaonyesha unasafiri umbali sawa wa usawa kati ya uangazavyo. Hii ni kwa sababu hakuna nguvu za ziada kwenye mpira katika mwelekeo usio na usawa baada ya kutupwa. Matokeo haya inamaanisha kasi ya usawa ni ya mara kwa mara na haiathiriwa na mwendo wima wala kwa mvuto (ambayo ni wima). Kumbuka kesi hii ni kweli kwa hali nzuri tu. Katika ulimwengu wa kweli, upinzani wa hewa huathiri kasi ya mipira kwa njia zote mbili.

Njia mbili-dimensional curved ya mpira usawa kutupwa linajumuisha mbili kujitegemea mwelekeo mmoja (usawa na wima). Funguo la kuchambua mwendo huo, unaoitwa mwendo wa projectile, ni kutatua katika mwendo pamoja na maelekezo ya perpendicular. Kutatua mwendo mbili-dimensional katika vipengele perpendicular inawezekana kwa sababu vipengele ni huru.