6.3: Kuelezea Sheria ya Gauss

Last updated
Save as PDF

Page ID: 176069

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Sheria ya hali ya Gauss
Eleza masharti ambayo sheria ya Gauss inaweza kutumika
Tumia sheria ya Gauss katika mifumo inayofaa

Sasa tunaweza kuamua mtiririko wa umeme kwa njia ya uso uliofungwa kwa sababu ya usambazaji wa malipo ya kiholela. Tuligundua kwamba ikiwa uso uliofungwa hauna malipo yoyote ndani ambapo mstari wa shamba la umeme unaweza kusitisha, basi mstari wowote wa shamba la umeme unaoingia kwenye uso wakati mmoja lazima lazima uondoke kwenye sehemu nyingine ya uso. Kwa hiyo, ikiwa uso uliofungwa hauna mashtaka yoyote ndani ya kiasi kilichofungwa, basi umeme wa umeme kupitia uso ni sifuri. Sasa, ni nini kinachotokea kwa umeme wa umeme ikiwa kuna mashtaka fulani ndani ya kiasi kilichofungwa? Sheria ya Gauss inatoa jibu la kiasi kwa swali hili.

Ili kujisikia kwa nini cha kutarajia, hebu tuhesabu mtiririko wa umeme kupitia uso wa spherical karibu na malipo mazuri ya uhakika\(q\), kwa kuwa tayari tunajua uwanja wa umeme katika hali kama hiyo. Kumbuka kwamba tunapoweka malipo ya uhakika kwa asili ya mfumo wa kuratibu, uwanja wa umeme kwa hatua\(P\) ambayo\(r\) iko mbali na malipo ya asili hutolewa na

\[\vec{E}_p = \dfrac{1}{4\pi \epsilon_0}\dfrac{q}{r^2}\hat{r},\]

\(\hat{r}\)wapi vector radial kutoka malipo katika asili kwa uhakika P. tunaweza kutumia uwanja huu wa umeme ili kupata mtiririko kupitia uso wa mviringo wa radius r, kama inavyoonekana kwenye Mchoro\(\PageIndex{1}\).

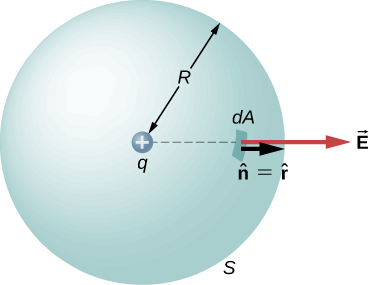
Aina iliyoandikwa S na radius R inavyoonyeshwa. Katika kituo chake, ni mduara mdogo na ishara plus, kinachoitwa q. kiraka ndogo kwenye nyanja ni kinachoitwa dA. Mishale miwili inaelekeza nje kutoka hapa, perpendicular kwa uso wa nyanja. mshale ndogo ni kinachoitwa n kwamba sawa na r kofia. Mshale mrefu umeandikwa vector E. — Kielelezo\(\PageIndex{1}\): Uso wa mviringo uliofungwa unaozunguka malipo ya uhakika q.

Kisha tunaomba\(\Phi = \int_S \vec{E} \cdot \hat{n} dA\) kwenye mfumo huu na mbadala inayojulikana maadili. Juu ya nyanja,\(\hat{n}\) na\(r = R\) hivyo kwa eneo infinitesimal da,

\[\begin{align*} d\Phi &= \vec{E} \cdot \hat{n} dA \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} \hat{r} \cdot \hat{r} dA \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} dA. \end{align*}\]

Sasa tunapata flux ya wavu kwa kuunganisha flux hii juu ya uso wa nyanja:

\[\Phi = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} \oint_S dA = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} (4\pi R^2) = \dfrac{q}{\epsilon_0}.\]

ambapo eneo la jumla la uso wa spherical ni\(4\pi R^2\). Hii inatoa flux kwa njia ya uso imefungwa spherical katika radius\(r\) kama

\[\Phi = \dfrac{q}{\epsilon_0}.\]

Ukweli wa ajabu juu ya equation hii ni kwamba flux ni huru ya ukubwa wa uso spherical. Hii inaweza kuhusishwa moja kwa moja na ukweli kwamba uwanja wa umeme wa malipo ya uhakika hupungua kama\(1/r^2\) kwa umbali, ambayo inafuta tu\(r^2\) kiwango cha ongezeko la eneo la uso.

Umeme Field Lines Picha

Njia mbadala ya kuona kwa nini kuenea kwa njia ya uso uliofungwa imefungwa ni huru ya eneo la uso ni kuangalia mistari ya shamba la umeme. Kumbuka kwamba kila mstari shamba kutoka q kwamba pierces uso katika radius\(R_1\) pia pierces uso katika\(R_2\) (Kielelezo\(\PageIndex{2}\)).

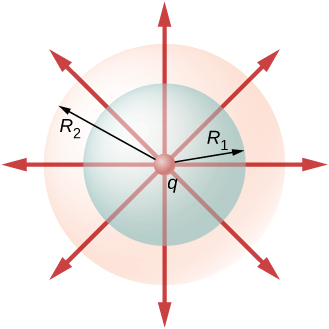
Kielelezo kinaonyesha miduara mitatu ya makini. Mdogo zaidi katikati ni kinachoitwa q, katikati ina radius R1 na moja kubwa ina radius R2. Mishale nane huangaza nje kutoka katikati katika pande zote nane. — Kielelezo\(\PageIndex{2}\): Flux kupitia nyuso za mviringo za radii\(R_1\) na\(R_2\) **kuzingatia malipo q** ni sawa, bila kujitegemea ukubwa wa uso, kwa kuwa mistari yote ya E -shamba ambayo hupiga uso mmoja kutoka ndani na mwelekeo wa nje pia hupiga uso mwingine katika mwelekeo huo.

Kwa hiyo, idadi halisi ya mistari ya shamba la umeme inayopitia nyuso mbili kutoka ndani hadi nje ya mwelekeo ni sawa. Hii nambari halisi ya mistari ya uwanja wa umeme, ambayo hupatikana kwa kutoa idadi ya mistari katika mwelekeo kutoka nje hadi ndani kutoka kwa idadi ya mistari katika mwelekeo kutoka ndani hadi nje hutoa kipimo cha kuona cha mtiririko wa umeme kupitia nyuso.

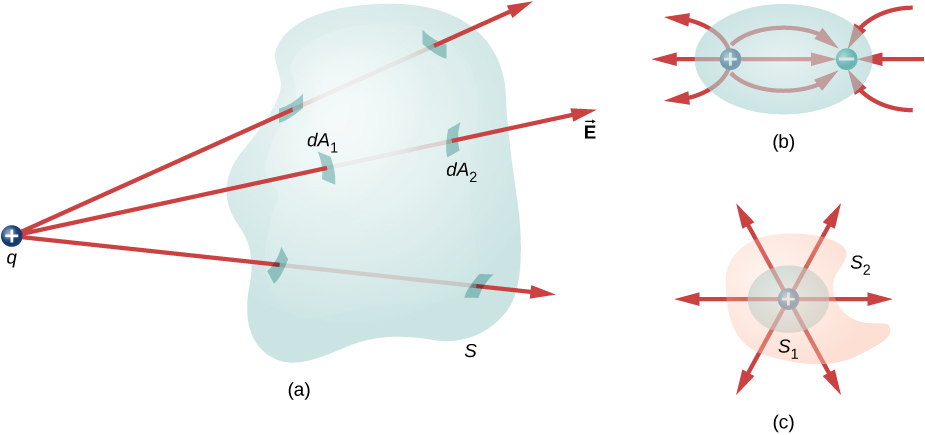
Unaweza kuona kwamba ikiwa hakuna mashtaka yanajumuishwa ndani ya uso uliofungwa, basi umeme wa umeme kwa njia hiyo lazima iwe sifuri. Mstari wa shamba la kawaida huingia kwenye uso\(dA_1\) na huacha\(dA_2\). Kila mstari unaoingia kwenye uso lazima pia uondoke kwenye uso huo. Hivyo “mtiririko” wa wavu wa mistari ya shamba ndani au nje ya uso ni sifuri (Kielelezo\(\PageIndex{3a}\)). Kitu kimoja kinachotokea ikiwa mashtaka ya ishara sawa na kinyume yanajumuishwa ndani ya uso uliofungwa, ili malipo ya jumla yamejumuishwa ni sifuri (Kielelezo\(\PageIndex{3b}\)). Upeo unaojumuisha kiasi sawa cha malipo una idadi sawa ya mistari ya shamba inayovuka, bila kujali sura au ukubwa wa uso, kwa muda mrefu kama uso unavyozingatia kiasi sawa cha malipo (Kielelezo\(\PageIndex{3c}\)).

Kielelezo a inaonyesha kawaida 3 dimensional sura kinachoitwa S. mduara ndogo na ishara pamoja, kinachoitwa q ni nje yake. Mishale mitatu iliyoandikwa vector E hutoka q na kupita kwa njia ya S. patches ambapo mishale kutoboa uso wa S ni yalionyesha. Kiraka ambapo mshale mmoja unaingia katika sura ni kinachoitwa Da1 na kiraka ambapo mshale unaojitokeza kutoka kwa umbo ni kinachoitwa Da2. Kielelezo b kinaonyesha mviringo na miduara miwili ndogo ndani yake. Hizi ni lebo pamoja na minus. Mshale wa tatu kutoka nje ya hatua ya mviringo hadi kwenye mduara ulioandikwa. Mishale mitatu inaelezea kutoka kwa pamoja hadi chini. Mishale mitatu inaelezea kutoka pamoja na nje ya mviringo. Kielelezo c ina sura isiyo ya kawaida iliyoandikwa S2. Ndani yake ni mduara unaoitwa S1. Katika kituo chake ni mduara mdogo unaoitwa pamoja. Mishale sita huangaza nje kutoka hapa kwa njia tofauti. — Kielelezo\(\PageIndex{3}\): Kuelewa mtiririko katika suala la mistari ya shamba. (a) Umeme wa umeme kupitia uso uliofungwa kutokana na malipo nje ya uso huo ni sifuri. (b) Mashtaka yanafungwa, lakini kwa sababu malipo ya wavu yanajumuishwa ni sifuri, mtiririko wa wavu kupitia uso uliofungwa pia ni sifuri. (c) Sura na ukubwa wa nyuso zinazozunguka malipo haijalishi kwa sababu nyuso zote zinazozunguka malipo sawa zina sawa.

Taarifa ya Sheria ya Gauss

Sheria ya Gauss inazalisha matokeo haya kwa kesi ya idadi yoyote ya mashtaka na eneo lolote la mashtaka katika nafasi ndani ya uso uliofungwa. Kwa mujibu wa sheria ya Gauss, mtiririko wa shamba la umeme kwa\(\vec{E}\) njia ya uso wowote uliofungwa, pia huitwa uso wa Gaussia, ni sawa na malipo ya wavu yaliyofungwa\((q_{enc})\) imegawanywa na permittivity ya nafasi ya bure\((\epsilon_0)\):

\[\Phi_{Closed \, Surface} = \dfrac{q_{enc}}{\epsilon_0}.\]

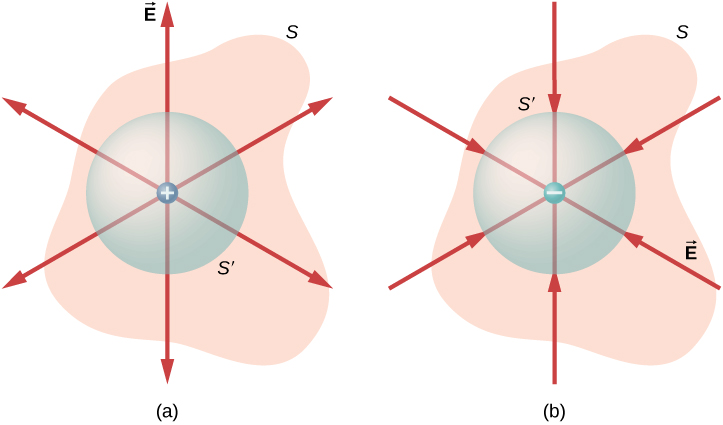
Equation hii inashikilia mashtaka ya ishara ama, kwa sababu sisi kufafanua eneo vector ya uso kufungwa kwa uhakika nje. Ikiwa malipo yaliyofungwa ni hasi (Kielelezo\(\PageIndex{4b}\)), basi mtiririko kupitia ama\(S\) au\(S'\) ni hasi.

Kielelezo a ina sura ya kawaida kinachoitwa S. ndani yake ni mduara kinachoitwa S mkuu. Katika kituo chake ni mduara mdogo unaoitwa pamoja. Mishale sita huangaza nje kutoka hapa kwa njia tofauti. Kielelezo b ina sawa kawaida sura S na mduara S mkuu. Katika kituo chake ni mduara mdogo unaoitwa minus. Mishale sita kutoka kwa mwelekeo tofauti huangaza ndani hadi chini. — Kielelezo\(\PageIndex{4}\): Flux umeme kupitia uso wowote uliofungwa unaozunguka malipo ya uhakika q hutolewa na sheria ya Gauss. (a) Malipo yaliyoambatanishwa ni chanya. (b) Malipo yaliyofungwa ni hasi.

Uso wa Gaussia hauhitaji kuendana na kitu halisi, kimwili; kwa kweli, ni mara chache. Ni kujenga hisabati ambayo inaweza kuwa ya umbo lolote, mradi ni kufungwa. Hata hivyo, kwa kuwa lengo letu ni kuunganisha mzunguko juu yake, tunapenda kuchagua maumbo ambayo yanafanana sana.

Ikiwa mashtaka ni mashtaka ya uhakika, basi tunawaongeza tu. Ikiwa malipo yanaelezewa na usambazaji unaoendelea, basi tunahitaji kuunganisha ipasavyo ili kupata malipo ya jumla ambayo inakaa ndani ya kiasi kilichofungwa. Kwa mfano, mtiririko kupitia uso wa Gaussia\(S\) wa Kielelezo\(\PageIndex{5}\) ni

\[\Phi = (q_1 + q_2 + q_5)/\epsilon_0.\]

Kumbuka kwamba\(q_{enc}\) ni tu jumla ya mashtaka uhakika. Ikiwa usambazaji wa malipo uliendelea, tunahitaji kuunganisha ipasavyo ili kuhesabu malipo ya jumla ndani ya uso wa Gaussia.

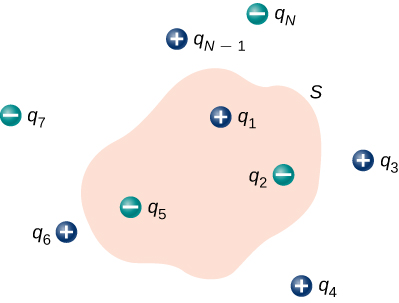
Kielelezo inaonyesha sura ya kawaida kinachoitwa S. ndani yake ni mashtaka kinachoitwa q1 chanya na q2 hasi na q5. Nje ya S ni mashtaka kinachoitwa chanya q3, q4, q6 na q N minus 1 na q7 hasi na q N. — Kielelezo\(\PageIndex{5}\): Kuongezeka kwa njia ya uso wa Gaussia umeonyeshwa, kutokana na usambazaji wa malipo, ni\(\Phi = (q_1 + q_2 + q_5)/\epsilon_0\).

Kumbuka kwamba kanuni ya superposition inashikilia shamba la umeme. Kwa hiyo, uwanja wa jumla wa umeme wakati wowote, ikiwa ni pamoja na wale walio kwenye uso wa Gaussia uliochaguliwa, ni jumla ya mashamba yote ya umeme yaliyopo katika hatua hii. Hii inaruhusu sisi kuandika sheria ya Gauss kwa suala la jumla ya uwanja wa umeme.

Sheria ya Gauss

Upepo\(\Phi\) wa shamba la umeme kwa\(\vec{E}\) njia ya uso wowote uliofungwa S (uso wa Gaussia) ni sawa na malipo ya wavu yaliyofungwa\((q_{enc})\) imegawanywa na permittivity ya nafasi ya bure\((\epsilon_0)\):

\[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = \dfrac{q_{enc}}{\epsilon_0}.\]

Kutumia sheria ya Gauss kwa ufanisi, lazima uwe na ufahamu wazi wa kile kila neno katika equation inawakilisha. Shamba\(\vec{E}\) ni shamba la umeme la jumla kila mahali kwenye uso wa Gaussia. Sehemu hii ya jumla inajumuisha michango kutoka kwa mashtaka ndani na nje ya uso wa Gaussia. Hata hivyo,\(q_{enc}\) ni malipo tu ndani ya uso Gaussia. Hatimaye, uso wa Gaussia ni uso wowote uliofungwa katika nafasi. Uso huo unaweza kufanana na uso halisi wa conductor, au inaweza kuwa uso wa kijiometri wa kufikiri. Mahitaji pekee yaliyowekwa kwenye uso wa Gaussia ni kwamba imefungwa (Kielelezo\(\PageIndex{5}\)).

Kielelezo kinaonyesha chupa inayoonekana kama chupa ya kichwa chini ambayo shingo imeenea, imeinama juu, inaendelea, imechukuliwa ndani ya chupa na kuunganishwa na msingi wake, hivyo kuwa na uso mmoja tu. — Kielelezo\(\PageIndex{6}\): **Chupa ya Klein** iliyojaa sehemu ya kioevu. Je! Chupa ya Klein inaweza kutumika kama uso wa Gaussia?

Mfano\(\PageIndex{1}\): Electric Flux through Gaussian Surfaces

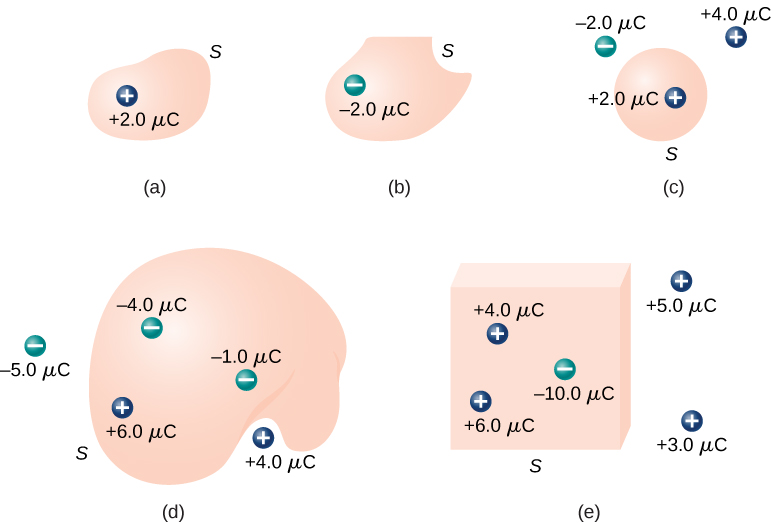
Tumia mzunguko wa umeme kupitia kila uso wa Gaussia umeonyeshwa kwenye Kielelezo\(\PageIndex{7}\).

Takwimu kupitia d kuonyesha maumbo ya kawaida na takwimu e inaonyesha mchemraba. Kielelezo a ina malipo ndani ya sura labeled pamoja 2.0 mu C. Kielelezo b ina malipo ndani ya sura labeled bala 2.0 mu C. takwimu c ina malipo ndani ya sura kinachoitwa pamoja 2.0 mu C na mashtaka mawili nje labeled pamoja 4 mu C na bala 2.0 mu C. takwimu d ina mashtaka tatu ndani ya sura labeled bala 1.0 mu C, bala 4.0 mu C na pamoja 6.0 mu C na mashtaka mawili nje ya sura iliyoandikwa bala 5.0 mu C na pamoja 4.0 mu C. Kielelezo e ina mashtaka matatu ndani ya kinachoitwa pamoja 4.0 mu C, pamoja na 6.0 mu C na bala 10.0 mu C na mashtaka mawili nje mchemraba kinachoitwa pamoja 5.0 mu C na 3.0 mu C. — Kielelezo\(\PageIndex{7}\): Nyuso mbalimbali za Gaussia na mashtaka.

Mkakati

Kutoka kwa sheria ya Gauss, mtiririko kupitia kila uso hutolewa na\(q_{enc}/\epsilon_0\), wapi\(q_{enc}\) malipo yaliyofungwa na uso huo.

Suluhisho

Kwa nyuso na mashtaka yaliyoonyeshwa, tunaona

a\(\Phi = \frac{2.0 \, \mu C}{\epsilon_0} = 2.3 \times 10^5 N \cdot m^2/C\).

b\(\Phi = \frac{-2.0 \, \mu C}{\epsilon_0} = -2.3 \times 10^5 N \cdot m^2/C\).

c\(\Phi = \frac{2.0 \, \mu C}{\epsilon_0} = 2.3 \times 10^5 N \cdot m^2/C\).

d\(\frac{-4.0 \, \mu C + 6.0 \, \mu C - 1.0 \, \mu C}{\epsilon_0} = 1.1 \times 10^5 N \cdot m^2/C\).

e\(\frac{4.0 \, \mu C + 6.0 \, \mu C - 10.0 \, \mu C}{\epsilon_0} = 0\).

Umuhimu

Katika kesi maalum ya uso uliofungwa, mahesabu ya mtiririko huwa jumla ya mashtaka. Katika sehemu inayofuata, hii itatuwezesha kufanya kazi na mifumo ngumu zaidi.

Zoezi\(\PageIndex{1}\)

Tumia mzunguko wa umeme kwa njia ya uso uliofungwa wa cubical kwa kila usambazaji wa malipo unaoonyeshwa kwenye Kielelezo\(\PageIndex{8}\).

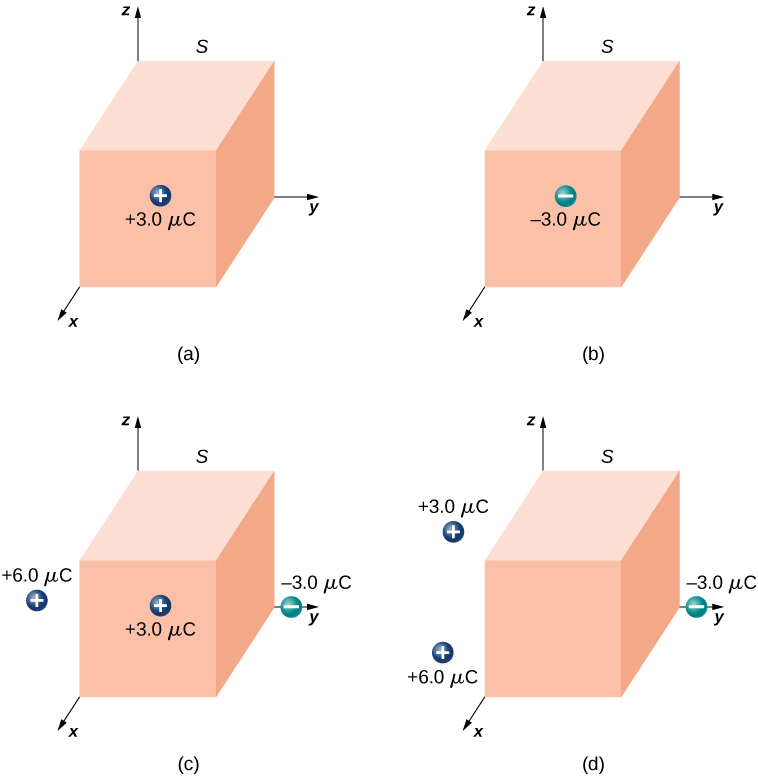
Takwimu a kupitia d zinaonyesha cuboid na kona moja kwa asili ya safu za kuratibu. Katika takwimu a, kuna malipo pamoja na 3.0 mu C juu ya uso sambamba na ndege ya yz. Katika takwimu b, kuna malipo ya chini ya 3.0 mu C juu ya uso sawa na ndege ya yz. Katika takwimu c, kuna malipo pamoja na 3.0 mu C juu ya uso sambamba na ndege ya yz, malipo ya chini ya 3.0 mu C kwenye mhimili y nje ya sura na malipo pamoja na 6.0 mu C nje ya sura. Katika takwimu d, kuna malipo ya chini ya 3.0 mu C kwenye mhimili y nje ya sura na mashtaka pamoja na 3.0 mu C na pamoja na 6.0 mu C nje ya sura. — Kielelezo\(\PageIndex{8}\): uso wa Gaussia wa cubical na mgawanyo mbalimbali wa malipo.

Jibu: \(3.4 \times 10^5 N \cdot m^2/C\)
Jibu b: \(-3.4 \times 10^5 N \cdot m^2/C\)
Jibu c: \(3.4 \times 10^5 N \cdot m^2/C\)
Jibu d: 0

Tumia simulation hii ili kurekebisha ukubwa wa malipo na eneo la uso wa Gaussia karibu nayo. Angalia jinsi hii inathiri mtiririko wa jumla na ukubwa wa shamba la umeme kwenye uso wa Gaussia.