6.2: Umeme Flux

Last updated
Save as PDF

Page ID: 176110

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Eleza dhana ya kuenea
Eleza umeme wa umeme
Tumia flux ya umeme kwa hali fulani

Dhana ya kuenea inaelezea kiasi gani cha kitu kinachopitia eneo fulani. Zaidi rasmi, ni bidhaa ya dot ya shamba la vector (katika sura hii, uwanja wa umeme) na eneo. Unaweza kufikiria mzunguko wa shamba la umeme kama kipimo cha idadi ya mistari ya shamba la umeme inayopitia eneo (Kielelezo\(\PageIndex{1}\)). Eneo kubwa, mistari zaidi ya shamba hupitia na, kwa hiyo, zaidi ya kuongezeka; vile vile, nguvu ya shamba la umeme ni (inayowakilishwa na wiani mkubwa wa mistari), zaidi ya kuongezeka. Kwa upande mwingine, ikiwa eneo limezungushwa ili ndege iendane na mistari ya shamba, hakuna atakayepita na hakutakuwa na mtiririko.

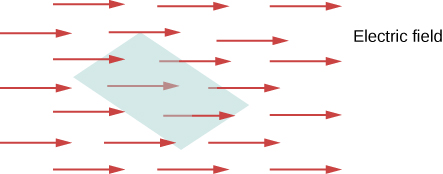
Kielelezo kinaonyesha eneo la kivuli katikati. Mishale kadhaa inayoelekeza haki huonyeshwa nyuma, mbele na kupitia eneo la kivuli. Hizi ni lebo uwanja wa umeme. — Kielelezo\(\PageIndex{1}\): Upepo wa shamba la umeme kupitia eneo la kivuli huchukua habari kuhusu “namba” ya mistari ya shamba la umeme inayopitia eneo hilo. Thamani ya namba ya mtiririko wa umeme inategemea ukubwa wa uwanja wa umeme na eneo hilo, pamoja na mwelekeo wa jamaa wa eneo hilo kuhusiana na mwelekeo wa uwanja wa umeme.

Mfano wa macroscopic ambayo inaweza kukusaidia kufikiria hii ni kuweka hula hoop katika mto unaozunguka. Unapobadilisha angle ya jamaa ya hoop na mwelekeo wa sasa, zaidi au chini ya mtiririko utaenda kupitia kitanzi. Vile vile, kiasi cha mtiririko kupitia kitanzi kinategemea nguvu ya sasa na ukubwa wa hoop. Tena, flux ni dhana ya jumla; tunaweza kuitumia pia kuelezea kiasi cha jua kinachopiga jopo la jua au kiasi cha nishati darubini inapokea kutoka nyota ya mbali, kwa mfano.

Kupima wazo hili, Kielelezo\(\PageIndex{1a}\) inaonyesha planar uso\(S_1\) wa eneo\(A_1\) hilo ni perpendicular kwa uwanja sare umeme\(\vec{E} = E\hat{y}\). Ikiwa mistari ya shamba N inapita\(S_1\), basi tunajua kutokana na ufafanuzi wa mistari ya shamba la umeme (Mashtaka ya Umeme na Mashamba) kwamba\(N/A \propto E\), au\(N \propto EA_1\).

Kiasi\(EA_1\) ni mtiririko wa umeme kupitia\(S_1\). Tunawakilisha umeme wa umeme kupitia uso wazi kama\(S_1\) kwa ishara\(\Phi\). Flux ya umeme ni kiasi cha scalar na ina kitengo cha SI cha mita za newton za mraba kwa kila coulomb (\(N \cdot m^2/C\)). Kumbuka kwamba pia\(N \propto EA_1\) inaweza kuandikwa kama\(N \propto \Phi\), kuonyesha kwamba umeme flux ni kipimo cha idadi ya mistari shamba kuvuka uso.

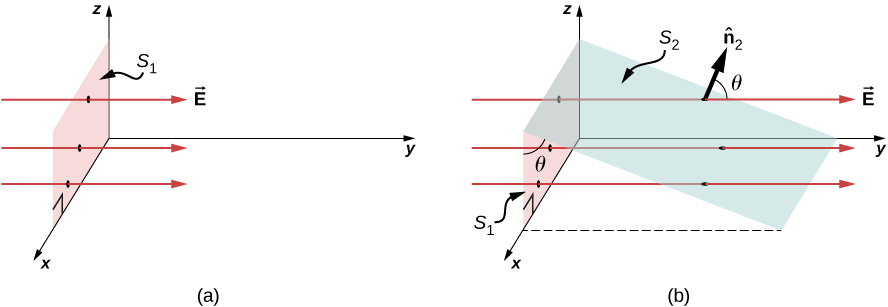
Kielelezo a inaonyesha eneo la kivuli cha mstatili katika ndege ya xz. Hii ni kinachoitwa S1. Kuna mishale mitatu iliyoandikwa E inayopita kupitia S1. Wao ni sawa na mhimili y na kumweka pamoja na mhimili y chanya. Kielelezo b, pia ina ndege S1 na mishale E. ndege nyingine, kinachoitwa S2 huunda theta angle na ndege S1. Mstari wao wa makutano ni sawa na mhimili x. Mshale ulioandikwa juu ya kuwa 2 huunda theta ya angle na E. — Kielelezo\(\PageIndex{2}\): (a) Eneo la eneo\(S_1\) la eneo\(A_1\) ni perpendicular kwa uwanja wa umeme\(E\hat{j}\). N shamba mistari msalaba uso\(S_1\). (b) Eneo\(S_2\) la eneo\(A_2\) ambalo makadirio kwenye ndege ya xz ni\(S_1\). Idadi sawa ya mistari ya shamba huvuka kila uso.

Sasa fikiria uso wa mipango ambayo sio perpendicular kwa shamba. Tunawezaje kuwakilisha umeme wa umeme? Kielelezo\(\PageIndex{2b}\) kinaonyesha uso\(S_2\) wa eneo\(A_2\) ambalo linaelekezwa kwa pembe\(\theta\) kwa xz -ndege na ambao makadirio yake katika ndege hiyo ni\(S_1\) (eneo\(A_1\)). Maeneo yanahusiana na\(A_2 \, cos \, \theta = A_1\). Kwa sababu idadi sawa ya mistari ya shamba huvuka wote\(S_1\) na\(S_2\), fluxes kupitia nyuso zote mbili lazima iwe sawa. Flux kwa njia hiyo\(S_2\) ni\(\Phi = EA_1 = EA_2 \, cos \, \theta\). Kuteua\(\hat{n}_2\) kama vector kitengo kawaida kwa\(S_2\) (angalia Kielelezo\(\PageIndex{2b}\)), sisi kupata

\[\Phi = \vec{E} \cdot \hat{n}_2 A_2.\]

Kumbuka

Angalia video hii ili uangalie kinachotokea kwa mtiririko kama eneo linabadilika kwa ukubwa na angle, au shamba la umeme linabadilika kwa nguvu.

Eneo Vector

Kwa kujadili mtiririko wa shamba la vector, ni muhimu kuanzisha vector eneo\(\vec{A}\). Hii inaruhusu sisi kuandika equation mwisho katika fomu zaidi kompakt. Je! Ukubwa wa vector eneo unapaswa kuwa nini? Je! Mwelekeo wa vector eneo unapaswa kuwa nini? Je, ni matokeo gani ya jinsi unavyojibu swali la awali?

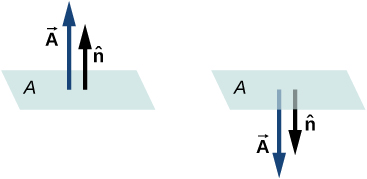
Vector eneo la uso gorofa wa eneo A ina ukubwa na mwelekeo wafuatayo:

Ukubwa ni sawa na eneo (A)
Mwelekeo ni pamoja na kawaida kwa uso\((\hat{n})\); yaani, perpendicular kwa uso.

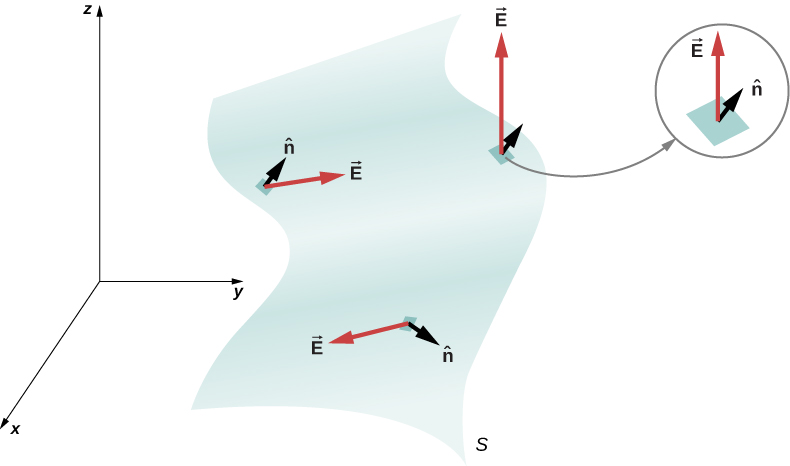
Kwa kuwa kawaida kwa uso wa gorofa inaweza kuelekeza katika mwelekeo wowote kutoka kwa uso, mwelekeo wa vector eneo la uso wazi unahitaji kuchaguliwa, kama inavyoonekana kwenye Mchoro\(\PageIndex{3}\).

Kielelezo inaonyesha ndege mbili usawa kinachoitwa A. kwanza ina mishale miwili akizungumzia juu kutoka ndege. tena ni kinachoitwa vector A na mfupi ni kinachoitwa n kofia. Ndege ya pili ina mishale miwili ileile inayoelekeza chini kutoka ndege. — Kielelezo\(\PageIndex{3}\): Mwelekeo wa vector eneo la uso wazi unahitaji kuchaguliwa; inaweza kuwa mojawapo ya kesi mbili zilizoonyeshwa hapa. Vector eneo la sehemu ya uso uliofungwa hufafanuliwa kwa uhakika kutoka ndani ya nafasi iliyofungwa kwa nje. Sheria hii inatoa mwelekeo wa kipekee.

Kwa kuwa\(\hat{n}\) ni kitengo kawaida kwa uso, ina maelekezo mawili iwezekanavyo katika kila hatua juu ya uso kwamba (Kielelezo\(\PageIndex{1a}\)). Kwa uso wazi, tunaweza kutumia mwelekeo wowote, kwa muda mrefu kama sisi ni thabiti juu ya uso mzima. \(\PageIndex{1c}\)ya takwimu inaonyesha kesi kadhaa.

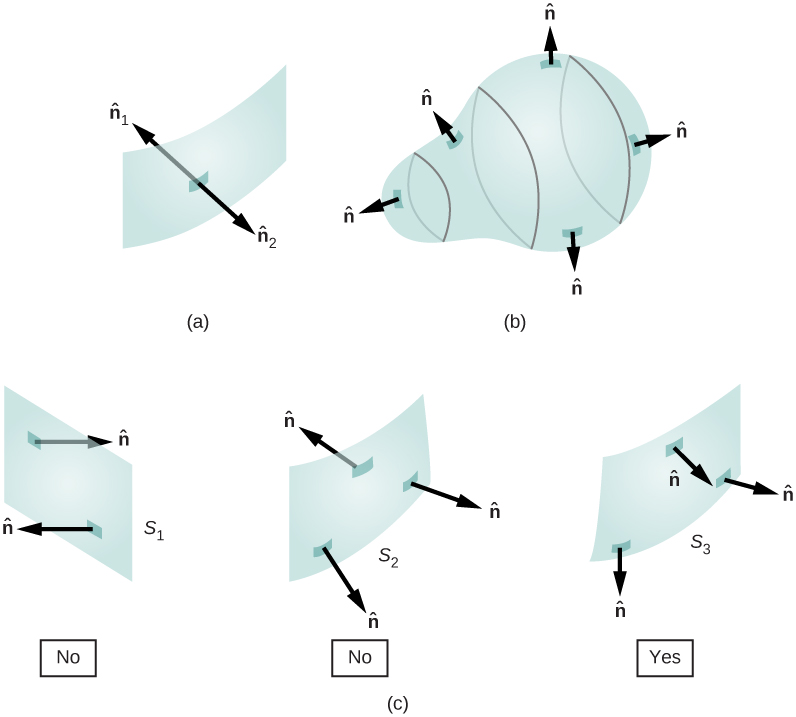
Kielelezo a inaonyesha uso wa mstatili wa mviringo. Mishale miwili inatoka kwenye hatua katika kituo chake na inaelezea kwa njia tofauti. Wote wawili ni perpendicular kwa uso. Wao ni kinachoitwa juu ya kofia 1 na katika kile 2. Kielelezo b kinaonyesha uso wa mwelekeo wa 3 ulioumbwa kiasi fulani kama bomba la mwanga. Kuna mishale mitano iliyoandikwa kwenye kofia, ambayo hutoka kwa pointi mbalimbali juu ya uso na inaelezea nje, perpendicular kwa uso. Kielelezo c inaonyesha nyuso tatu mstatili kinachoitwa S1, S2 na S3. Mishale miwili iliyoandikwa kwenye kofia ni perpendicular kwa S1 na inaelezea kwa njia tofauti. Mishale mitatu iliyoandikwa n kofia ni perpendicular kwa S2, moja akizungumzia katika mwelekeo kinyume na wengine wawili. Kuna mishale mitatu perpendicular kwa S3. Wote wanasema nje kutoka upande mmoja wa uso. — Kielelezo\(\PageIndex{4}\): (a) Vectors mbili uwezo wa kawaida kutokea katika kila hatua juu ya uso. (b) Kawaida ya nje hutumiwa kuhesabu mtiririko kupitia uso uliofungwa. (c) Tu\(S_3\) imepewa seti thabiti ya vectors kawaida ambayo inaruhusu sisi kufafanua flux kupitia uso.

Hata hivyo, ikiwa uso umefungwa, basi uso unazunguka kiasi. Katika hali hiyo, mwelekeo wa vector kawaida wakati wowote juu ya pointi uso kutoka ndani na nje. On uso kufungwa kama vile ya Kielelezo\(\PageIndex{1b}\),\(\hat{n}\) amechaguliwa kuwa nje ya kawaida katika kila hatua, kuwa thabiti na mkataba ishara kwa ajili ya malipo ya umeme.

umeme flux

Sasa kwa kuwa tumeelezea vector ya eneo la uso, tunaweza kufafanua upepo wa umeme wa shamba la umeme sare kupitia eneo la gorofa kama bidhaa ya scalar ya shamba la umeme na vector eneo:

\[\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \hat{E}, \, flat \, surface).\]

Kielelezo\(\PageIndex{5}\) kinaonyesha uwanja wa umeme wa mfumo wa kushtakiwa kinyume, sambamba-sahani na sanduku la kufikiri kati ya sahani. Shamba la umeme kati ya sahani ni sare na pointi kutoka sahani nzuri kuelekea sahani hasi. Mahesabu ya mtiririko wa shamba hili kupitia nyuso mbalimbali za sanduku inaonyesha kwamba mtiririko wa wavu kupitia sanduku ni sifuri. Kwa nini flux kufuta nje hapa?

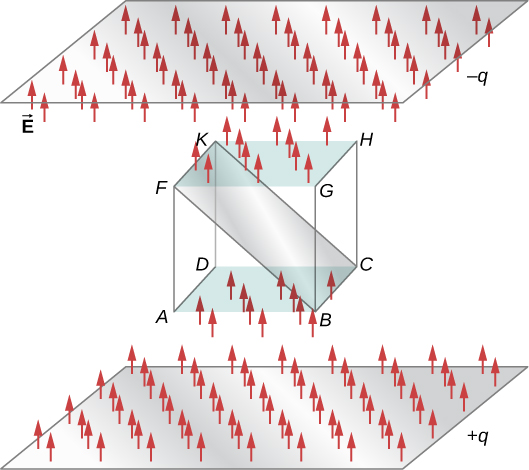
ABCDKFGH mchemraba inavyoonekana katika kituo. Ndege ya diagonal inavyoonyeshwa ndani yake kutoka KF hadi BC. Upeo wa juu wa mchemraba, FGHK ina ndege iliyoitwa minus q kidogo juu yake na sambamba nayo. Vile vile, ndege nyingine inaitwa pamoja na q inavyoonyeshwa kidogo chini ya uso wa chini wa mchemraba, sawa na hilo. Mishale midogo nyekundu inavyoonyeshwa juu kutoka ndege ya chini, ikizungumzia juu ya uso wa chini wa mchemraba, akielezea juu kutoka kwenye uso wa juu wa mchemraba na kuelekeza hadi ndege ya juu. Hizi ni kinachoitwa vector E. — Kielelezo\(\PageIndex{5}\): Umeme wa umeme kupitia mchemraba, umewekwa kati ya sahani mbili za kushtakiwa. Umeme wa umeme kupitia uso wa chini (**ABCD**)\(\vec{E}\) ni hasi, kwa sababu iko kinyume na kawaida kwa uso. Flux umeme kupitia uso wa juu (**FGHK**) ni chanya, kwa sababu uwanja wa umeme na kawaida ni katika mwelekeo huo. Flux umeme kupitia nyuso nyingine ni sifuri, kwani uwanja wa umeme ni perpendicular kwa vectors kawaida ya nyuso hizo. Umeme wa umeme wa wavu kupitia mchemraba ni jumla ya fluxes kupitia nyuso sita. Hapa, mtiririko wa wavu kupitia mchemraba ni sawa na sifuri. Ukubwa wa mtiririko kupitia mstatili **BCKF** ni sawa na ukubwa wa flux kupitia nyuso zote za juu na chini.

Sababu ni kwamba vyanzo vya uwanja wa umeme ni nje ya sanduku. Kwa hiyo, ikiwa mstari wowote wa shamba la umeme huingia kiasi cha sanduku, lazima pia uondoke mahali fulani juu ya uso kwa sababu hakuna malipo ndani ya mistari ya kutua. Kwa hiyo, kwa ujumla, umeme wa umeme kupitia uso uliofungwa ni sifuri ikiwa hakuna vyanzo vya shamba la umeme, ikiwa ni chanya au hasi, ndani ya kiasi kilichofungwa. Kwa ujumla, wakati mistari ya shamba ikitoka (au “hutoka nje”) uso uliofungwa,\(\Phi\) ni chanya; wanapoingia (au “kuingia ndani”) uso,\(\Phi\) ni hasi.

Uso wowote wa laini, usio na gorofa unaweza kubadilishwa na mkusanyiko wa vidogo, takriban nyuso za gorofa, kama inavyoonekana kwenye Mchoro\(\PageIndex{6}\). Ikiwa tunagawanya uso S ndani ya patches ndogo, basi tunaona kwamba, kama patches kuwa ndogo, zinaweza kuhesabiwa na nyuso za gorofa. Hii ni sawa na jinsi tunavyotambua uso wa Dunia kama bapa ya ndani, ingawa tunajua kwamba duniani kote, ni takriban spherical.

Kielelezo inaonyesha uso WAVY kinachoitwa S. mishale mitatu kinachoitwa n kwamba yanatokana na patches tatu tofauti juu ya uso. Longer mishale lebo vector E pia yanatokana na kila kiraka. Mtazamo ulioenea wa kiraka kimoja unaonyeshwa upande. Inaonyesha juu ya nini kuwa perpendicular kwa kiraka. — Kielelezo\(\PageIndex{6}\): Uso umegawanywa katika patches ili kupata mtiririko.

Ili kuweka wimbo wa patches, tunaweza kuwahesabu kutoka 1 hadi N. Sasa, tunafafanua vector eneo kwa kila kiraka kama eneo la kiraka alisema katika mwelekeo wa kawaida. Hebu kuashiria eneo vector kwa ajili yao katika kiraka na\(\delta \vec{A}_i\). (Tumetumia ishara\(\delta\) kutukumbusha kwamba eneo hilo ni la kiraka kiholela kidogo.) Kwa patches ndogo za kutosha, tunaweza takriban shamba la umeme juu ya kiraka chochote kilichopewa kama sare. Hebu tuonyeshe uwanja wa umeme wa wastani katika eneo lao i the kiraka na\(\vec{E}_i\).

\[\vec{E}_i = \mathrm{average \, electric \, field \, over \, the \,} i \mathrm{th \, patch}.\]

Kwa hiyo, tunaweza kuandika umeme wa umeme\(\Phi\) kupitia eneo lao katika kiraka kama

\[\Phi_i = \vec{E}_i \cdot \delta \vec{A}_i \, (i \mathrm{th \, patch}).\]

Flux kupitia kila moja ya patches ya mtu binafsi inaweza kujengwa kwa namna hii na kisha kuongezwa ili kutupa makadirio ya flux wavu kupitia uso mzima S, ambayo sisi kuashiria tu kama\(\Phi\).

\[\Phi = \sum_{i=1}^N \Phi_i = \sum_{i=1}^N \vec{E}_i \cdot \delta \vec{A}_i \, (N \, patch \, estimate).\]

Makadirio haya ya mtiririko hupata bora kama tunapunguza ukubwa wa patches. Hata hivyo, unapotumia patches ndogo, unahitaji zaidi yao ili kufunika uso huo. Katika kikomo cha patches ndogo ndogo, zinaweza kuchukuliwa kuwa na eneo la dA na kitengo cha kawaida\(\hat{n}\). Kwa kuwa mambo ni infinitesimal, wanaweza kuwa kudhani kuwa planar, na\(\vec{E}_i\) inaweza kuchukuliwa kama mara kwa mara juu ya kipengele chochote. Kisha mtiririko\(d\Phi\) kupitia eneo la dA hutolewa na\(d\Phi = \vec{E} \cdot \hat{n} dA\). Ni chanya wakati angle kati\(\vec{E}_i\) na\(\hat{n}\) ni chini ya\(90^o\) na hasi wakati angle ni kubwa kuliko\(90^o\). Flux ya wavu ni jumla ya vipengele vidogo vya flux juu ya uso mzima. Kwa patches ndogo ndogo, unahitaji patches nyingi sana, na kikomo cha jumla kinakuwa muhimu. Kwa\(\int_S\) kuwakilisha muhimu juu ya S,

\[\Phi = \int_S \vec{E} \cdot \hat{n}dA = \int_S \vec{E} \cdot d\vec{A} \, (open \, surface).\]

Kwa maneno ya vitendo, integrals ya uso huhesabiwa kwa kuchukua antiderivatives ya vipimo vyote viwili vinavyofafanua eneo hilo, na kando ya uso katika swali kuwa mipaka ya muhimu.

Ili kutofautisha kati ya mtiririko kupitia uso wazi kama ule wa Kielelezo\(\PageIndex{2}\) na kuenea kwa njia ya uso uliofungwa (moja ambayo imepakana kabisa kiasi fulani), tunawakilisha kuenea kwa njia ya uso uliofungwa na

\[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = \oint_S \vec{E} \cdot d\vec{A} \, (closed \, surface)\]

ambapo mduara kupitia ishara muhimu ina maana tu kwamba uso umefungwa, na tunaunganisha juu ya jambo zima. Ikiwa unaunganisha tu juu ya sehemu ya uso uliofungwa, hiyo inamaanisha unachukua sehemu ndogo kama uso wazi.

Mfano\(\PageIndex{1}\): Flux of a Uniform Electric Field

Sehemu ya umeme ya mara kwa mara ya\(E_0\) pointi za ukubwa katika mwelekeo wa z -axis chanya (Kielelezo\(\PageIndex{7}\)). Je, ni umeme wa umeme kupitia mstatili na pande a na b katika (a) xy -ndege na katika (b) xz -ndege?

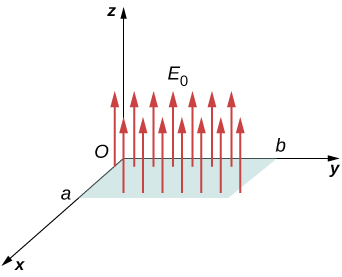
Kipande cha mstatili kinaonyeshwa kwenye ndege ya xy. Upande wake kando ya mhimili x ni wa urefu a na upande wake kando ya mhimili y ni wa urefu b Mishale iliyoandikwa E subscript 0 inatokana na ndege na kumweka katika mwelekeo mzuri z. — Kielelezo\(\PageIndex{7}\): Kuhesabu mtiririko wa\(E_0\) kupitia uso wa mstatili.

Mkakati

Tumia ufafanuzi wa kuenea:\(\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \vec{E})\), ambapo ufafanuzi wa bidhaa za dot ni muhimu.

Suluhisho

Katika kesi hii,\(\Phi = \vec{E}_0 \cdot \vec{A} = E_0 A = E_0 ab\).
Hapa, mwelekeo wa vector eneo ni ama pamoja na chanya y -axis au kuelekea hasi y -axis. Kwa hiyo, bidhaa ya scalar ya uwanja wa umeme na vector eneo ni sifuri, kutoa sifuri flux.

Umuhimu

Maelekezo ya jamaa ya uwanja wa umeme na eneo yanaweza kusababisha kuongezeka kwa eneo hilo kuwa sifuri.

Flux ya Shamba la Umeme Sare kupitia Uso uliofungwa

Sehemu ya umeme ya mara kwa mara ya\(E_0\) pointi za ukubwa katika mwelekeo wa z -axis chanya (Kielelezo\(\PageIndex{8}\)). Je, ni umeme wa umeme wa umeme kupitia mchemraba?

Mkakati

Tumia ufafanuzi wa kuenea:\(\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \vec{E})\), akibainisha kuwa uso uliofungwa hupunguza utata katika mwelekeo wa vector eneo.

Suluhisho

Kupitia uso wa juu wa mchemraba\(\Phi = \vec{E}_0 \cdot \vec{A} = E_0 A\).

Kupitia uso chini ya mchemraba,\(\Phi = \vec{E}_0 \cdot \vec{A} = - E_0 A\), kwa sababu eneo vector hapa pointi chini.

Pamoja na pande nyingine nne, mwelekeo wa vector eneo ni perpendicular kwa mwelekeo wa uwanja wa umeme. Kwa hiyo, bidhaa ya scalar ya uwanja wa umeme na vector eneo ni sifuri, kutoa sifuri flux.

Flux ya wavu ni\(\Phi_{net} = E_0A - E_0 A + 0 + 0 + 0 + 0 = 0\).

Umuhimu

Flux ya wavu ya shamba la umeme sare kupitia uso uliofungwa ni sifuri.

Mfano\(\PageIndex{3}\): Electric Flux through a Plane, Integral Method

Shamba la umeme\(\vec{E}\) la ukubwa wa 10 N/C linaelekezwa sambamba na ndege ya yz\(30^o\) juu ya ndege ya xy, kama inavyoonekana kwenye Mchoro\(\PageIndex{9}\). Je, ni umeme gani kupitia eneo la ndege la eneo\(6.0 \, m^2\) lililopo katika ndege ya xz? Kudhani kwamba\(\hat{n}\) pointi katika chanya y -mwelekeo.

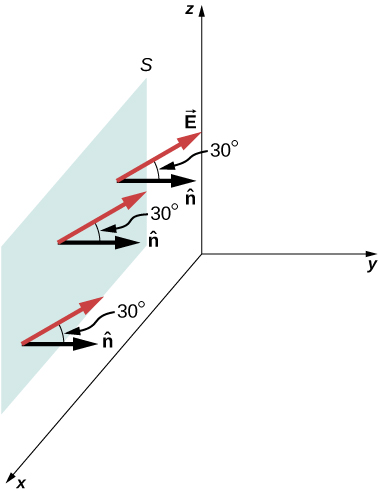
Uso wa mstatili S unaonyeshwa kwenye ndege ya xz. Mishale mitatu iliyoandikwa n inayotokana na pointi tatu juu ya uso na uhakika katika mwelekeo chanya y. Mishale mitatu tena iliyoandikwa vector E pia inatokana na pointi sawa. Wanafanya angle ya digrii 30 na kofia. — Kielelezo\(\PageIndex{9}\): Shamba la umeme linazalisha umeme wa umeme kwa njia ya uso S.

Mkakati

Tumia\(\Phi = \int_S \vec{E} \cdot \hat{n} dA\), ambapo mwelekeo na ukubwa wa uwanja wa umeme ni mara kwa mara.

Suluhisho

Pembe kati ya shamba la umeme sare\(\vec{E}\) na kitengo cha kawaida\(\hat{n}\) kwa uso wa mpango ni\(30^o\). Kwa kuwa mwelekeo na ukubwa wote ni mara kwa mara, E huja nje ya muhimu. Yote iliyoachwa ni muhimu ya uso juu ya dA, ambayo ni A. Kwa hiyo, kwa kutumia equation ya wazi ya uso, tunaona kwamba umeme wa umeme kupitia uso ni

\[\Phi = \int_S \vec{E} \cdot \hat{n} dA = EA \, cos \, \theta\]

\[= (10 \, N/C)(6.0 \, m^2)(cos \, 30^o) = 52 \, N \cdot m^2/C.\]

Umuhimu

Tena, maelekezo ya jamaa ya shamba na suala la eneo hilo, na usawa wa jumla na muhimu utafungua kwa bidhaa rahisi ya dot ya eneo na uwanja wa umeme.

Zoezi\(\PageIndex{1}\)

Je, kuna pembe gani kati ya uwanja wa umeme na uso unaoonyeshwa kwenye Kielelezo\(\PageIndex{9}\) katika mfano uliopita ili hakuna umeme wa umeme unapita kupitia uso?

Suluhisho

Weka ili kitengo chake cha kawaida kinapingana\(\vec{E}\).

Mfano\(\PageIndex{4}\) : Inhomogeneous Electric Field

Je, ni jumla ya jumla ya shamba la umeme\(\vec{E} = cy^2\hat{k}\) kupitia uso wa mstatili unaoonyeshwa kwenye Kielelezo\(\PageIndex{10}\)?

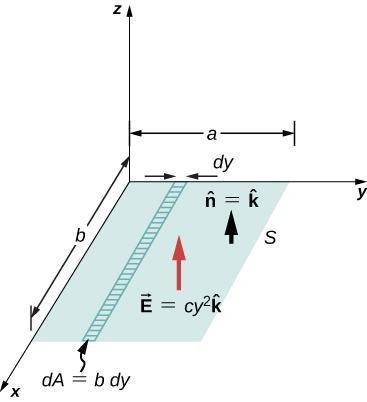
Mstatili ulioitwa S unaonyeshwa kwenye ndege ya xy. Upande wake pamoja na mhimili y ni wa urefu a na kwamba kando ya mhimili x hatua b. strip ni alama juu ya mstatili, na urefu wake sambamba na x axis. Urefu wake ni b na upana wake ni kavu. Eneo lake linaitwa dA sawa na b dy. Mishale miwili imeonyeshwa perpendicular kwa S, n kofia sawa na k kofia na vector E sawa na cy squared k kofia. Hizi hatua katika mwelekeo chanya z. — Kielelezo\(\PageIndex{10}\): Kwa kuwa uwanja wa umeme sio mara kwa mara juu ya uso, ushirikiano ni muhimu kuamua mtiririko.

Mkakati

Tumia\(\Phi = \int_S \vec{E} \cdot \hat{n}dA\). Tunadhani kwamba kitengo cha kawaida\(\hat{n}\) kwa pointi zilizopewa uso katika mwelekeo mzuri wa z, hivyo\(\hat{n} = \hat{k}\). Kwa kuwa shamba la umeme si sare juu ya uso, ni muhimu kugawanya uso ndani ya vipande vidogo ambavyo kimsingi\(\vec{E}\) ni mara kwa mara. Kama inavyoonekana katika Kielelezo\(\PageIndex{10}\), vipande hivi ni sawa na x -axis, na kila strip ina eneo\(dA = b \, dy\).

Suluhisho

Kutoka kwa uso wa wazi, tunaona kwamba mtiririko wa wavu kupitia uso wa mstatili ni

\[\begin{align*} \Phi &= \int_S \vec{E} \cdot \hat{n} dA = \int_0^a (cy^2 \hat{k}) \cdot \hat{k}(b \, dy) \\[4pt] &= cb \int_0^a y^2 dy = \frac{1}{3} a^3 bc. \end{align*}\]

Umuhimu

Kwa uwanja usio wa mara kwa mara wa umeme, njia muhimu inahitajika.

Zoezi\(\PageIndex{1}\)

Ikiwa uwanja wa umeme katika Mfano\(\PageIndex{4}\)\(\vec{E} = mx\hat{k}\) ni. ni nini mtiririko kupitia eneo la mstatili?

Suluhisho

\(mab^2/2\)