6.4: Kutumia Sheria ya Gauss

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza nini spherical, cylindrical, na planar ulinganifu ni
• Kutambua kama au mfumo fulani ana moja ya symmetries hizi
• Tumia sheria ya Gauss kuamua uwanja wa umeme wa mfumo na mojawapo ya symmetries hizi

Sheria ya Gauss inasaidia sana katika kuamua maneno kwa uwanja wa umeme, ingawa sheria si moja kwa moja kuhusu uwanja wa umeme; ni kuhusu umeme wa umeme. Inageuka kuwa katika hali ambazo zina ulinganifu fulani (spherical, cylindrical, au planar) katika usambazaji wa malipo, tunaweza kuthibitisha uwanja wa umeme kulingana na ujuzi wa mtiririko wa umeme. Katika mifumo hii, tunaweza kupata uso wa Gaussia S juu ya uwanja wa umeme una ukubwa wa mara kwa mara. Aidha, kama\(\vec{E}\) ni sambamba na\(\hat{n}\) kila mahali juu ya uso, basi\(\vec{E} \cdot \hat{n} = E\). (Kama\(\vec{E}\) na\(\hat{n}\) ni antiparallel kila mahali juu ya uso,\(\vec{E} \cdot \hat{n} = - E\).) Sheria ya Gauss kisha simplifies kwa

\[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = E \oint_S dA = EA = \dfrac{q_{enc}}{\epsilon_0},\]

ambapo A ni eneo la uso. Kumbuka kuwa ulinganifu huu husababisha mabadiliko ya uingizaji wa uingizaji katika bidhaa ya ukubwa wa shamba la umeme na eneo linalofaa. Unapotumia mtiririko huu katika maneno ya sheria ya Gauss, unapata equation ya algebraic ambayo unaweza kutatua kwa ukubwa wa shamba la umeme, ambalo linaonekana kama

\[E \approx \dfrac{q_{enc}}{\epsilon_0 \, area}.\]

Mwelekeo wa uwanja wa umeme kwenye hatua ya P hupatikana kutoka kwa ulinganifu wa usambazaji wa malipo na aina ya malipo katika usambazaji. Kwa hiyo, sheria ya Gauss inaweza kutumika kuamua\(\vec{E}\). Hapa ni muhtasari wa hatua tutakayofuata:

Mkakati wa kutatua matatizo: Sheria ya Gauss

1. Tambua ulinganifu wa anga wa usambazaji wa malipo. Hii ni hatua muhimu ya kwanza ambayo inaruhusu sisi kuchagua uso sahihi wa Gaussia. Kama mifano, malipo ya pekee ya uhakika yana ulinganifu wa spherical, na mstari usio wa malipo una ulinganifu wa cylindrical.
2. Chagua uso wa Gaussia na ulinganifu sawa na usambazaji wa malipo na kutambua matokeo yake. Kwa uchaguzi huu,\(\vec{E} \cdot \hat{n}\) ni rahisi kuamua juu ya uso Gaussia.
3. Tathmini muhimu\(\oint_S \vec{E} \cdot \hat{n} dA\) juu ya uso wa Gaussia, yaani, kuhesabu mtiririko kupitia uso. Ulinganifu wa uso wa Gaussia unatuwezesha kuzingatia\(\vec{E} \cdot \hat{n}\) nje ya muhimu.
4. Kuamua kiasi cha malipo kilichofungwa na uso wa Gaussia. Hii ni tathmini ya upande wa kulia wa equation inayowakilisha sheria ya Gauss. Mara nyingi ni muhimu kufanya ushirikiano ili kupata malipo yaliyofungwa.
5. Tathmini uwanja wa umeme wa usambazaji wa malipo. Shamba linaweza kupatikana sasa kwa kutumia matokeo ya hatua 3 na 4.

Kimsingi, kuna aina tatu tu za ulinganifu zinazoruhusu sheria ya Gauss kutumiwa kuthibitisha uwanja wa umeme. Wao ni

• Usambazaji wa malipo na ulinganifu wa spherical
• Usambazaji wa malipo na ulinganifu wa cylindrical
• Usambazaji wa malipo na ulinganifu wa mpango

Ili kutumia ulinganifu, tunafanya mahesabu katika mifumo sahihi ya kuratibu na kutumia aina sahihi ya uso wa Gaussia kwa ulinganifu huo, kwa kutumia hatua nne zilizobaki.

Usambazaji wa Malipo na Ulinganifu wa Spherical

Usambazaji wa malipo una ulinganifu wa spherical ikiwa wiani wa malipo unategemea tu umbali kutoka kwa uhakika katika nafasi na sio mwelekeo. Kwa maneno mengine, ikiwa unazunguka mfumo, hauonekani tofauti. Kwa mfano, ikiwa nyanja ya radius R inashtakiwa kwa usawa na wiani wa malipo\(\rho_0\) basi usambazaji una ulinganifu wa spherical (Kielelezo\(\PageIndex{1a}\)). Kwa upande mwingine, ikiwa nyanja ya radius R inashtakiwa ili nusu ya juu ya nyanja ina wiani wa malipo ya sare\(\rho_1\) na nusu ya chini ina wiani wa malipo ya sare,\(\rho_2 \neq \rho_1\) basi nyanja haina ulinganifu wa spherical, kwa sababu wiani wa malipo hutegemea mwelekeo (Kielelezo). \(\PageIndex{1b}\)). Hivyo, si umbo la kitu bali sura ya usambazaji wa malipo ambayo huamua kama au mfumo una ulinganifu wa spherical.

Kielelezo\(\PageIndex{1c}\) kinaonyesha nyanja yenye shells nne tofauti, kila mmoja na wiani wake wa malipo ya sare. Ingawa hii ni hali ambapo wiani wa malipo katika nyanja kamili sio sare, kazi ya wiani wa malipo inategemea tu umbali kutoka katikati na sio mwelekeo. Kwa hiyo, usambazaji huu wa malipo una ulinganifu wa spherical.

Kielelezo\(\PageIndex{1}\): Mifano ya mifumo ya spherically symmetrical na isiyo ya kawaida. Vivuli tofauti vinaonyesha densities tofauti za malipo. Malipo juu ya vitu vyenye umbo la spherically haimaanishi mashtaka yanasambazwa kwa ulinganifu wa spherical. Ulinganifu wa spherical hutokea tu wakati wiani wa malipo haukutegemea mwelekeo. Katika (a), mashtaka yanasambazwa kwa usawa katika nyanja. Katika (b), nusu ya juu ya nyanja ina wiani tofauti wa malipo kutoka nusu ya chini; kwa hiyo, (b) haina ulinganifu wa spherical. Katika (c), mashtaka yana katika shells za spherical za densities tofauti za malipo, ambayo ina maana kwamba wiani wa malipo ni kazi tu ya umbali wa radial kutoka katikati; kwa hiyo, mfumo una ulinganifu wa spherical.

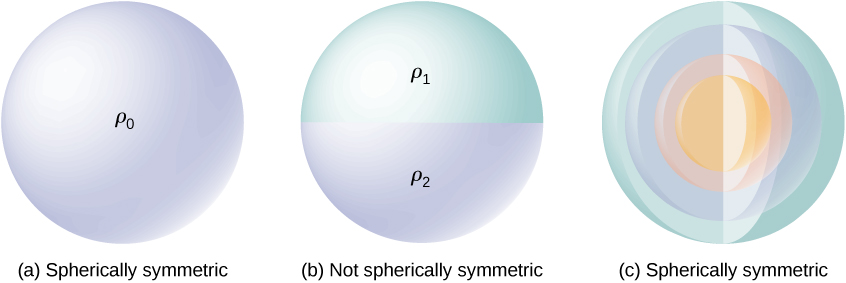
Njia moja nzuri ya kuamua kama tatizo lako lina ulinganifu wa spherical ni kuangalia kazi ya wiani wa malipo katika kuratibu za spherical,\(\rho(r, \theta, \phi)\). Ikiwa wiani wa malipo ni kazi tu ya r, yaani\(\rho = \rho(r)\), basi una ulinganifu wa spherical. Ikiwa wiani unategemea\(\theta\) au\(\phi\), unaweza kuibadilisha kwa mzunguko; kwa hiyo, huwezi kuwa na ulinganifu wa spherical.

Matokeo ya ulinganifu

Katika kesi zote za usawa, uwanja wa umeme wakati wowote lazima uelekezwe kwa radially, kwa sababu malipo na, kwa hiyo, shamba lazima liwe imara chini ya mzunguko. Kwa hiyo, kwa kutumia viwianishi vya spherical na asili yao katikati ya usambazaji wa malipo ya spherical, tunaweza kuandika fomu inayotarajiwa ya uwanja wa umeme kwenye hatua P iko umbali r kutoka katikati:

\[Spherical \, symmetry: \, \vec{E}_p = E_p(r)\hat{r},\]

\(\hat{r}\)wapi vector kitengo kilichoelekezwa katika mwelekeo kutoka kwa asili hadi hatua ya shamba P. Sehemu ya radial\(E_p\) ya uwanja wa umeme inaweza kuwa chanya au hasi. Wakati\(E_p > 0\), uwanja wa umeme kwenye P unasema mbali na asili, na wakati\(E_p < 0\), uwanja wa umeme kwenye P unaelezea kuelekea asili.

Gaussia uso na mahesabu ya flux

Sasa tunaweza kutumia fomu hii ya uwanja wa umeme ili kupata upepo wa shamba la umeme kupitia uso wa Gaussia. Kwa ulinganifu wa spherical, uso wa Gaussia ni uso wa mviringo uliofungwa ambao una kituo sawa na kituo cha usambazaji wa malipo. Kwa hiyo, mwelekeo wa eneo la vector ya kipengele cha eneo kwenye uso wa Gaussia wakati wowote ni sawa na mwelekeo wa uwanja wa umeme wakati huo, kwa kuwa wote wawili huelekezwa kwa radially nje (Kielelezo\(\PageIndex{2}\)).

Kielelezo\(\PageIndex{2}\): uwanja wa umeme wakati wowote wa uso wa Gaussia wa mviringo kwa usambazaji wa malipo ya usawa ni sawa na vector ya kipengele cha eneo hilo, ikitoa flux kama bidhaa ya ukubwa wa shamba la umeme na thamani ya eneo hilo. Kumbuka kuwa radius R ya usambazaji wa malipo na r radius ya uso wa Gaussia ni kiasi tofauti.

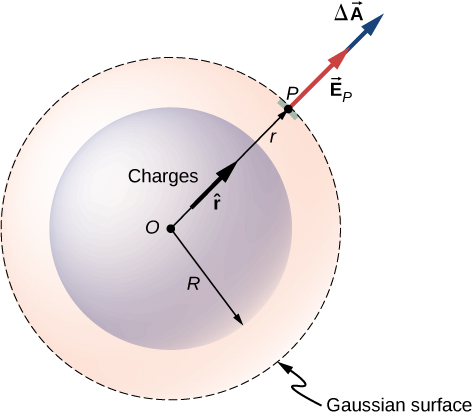
Ukubwa wa uwanja wa umeme\(\vec{E}\) lazima uwe sawa kila mahali kwenye uso wa Gaussia unaozingatia usambazaji. Kwa uso wa spherical wa radius r:

\[\Phi = \oint_S \vec{E}_p \cdot \hat{n} dA = E_p \oint_S dA = E_p \, 4\pi r^2.\]

Kutumia sheria ya Gauss

Kwa mujibu wa sheria ya Gauss, kuenea kwa njia ya uso uliofungwa ni sawa na malipo ya jumla yaliyofungwa ndani ya uso uliofungwa umegawanyika na permittivity ya utupu\(\epsilon_0\). Hebu\(q_{enc}\) kuwa malipo ya jumla yaliyofungwa ndani ya umbali r kutoka asili, ambayo ni nafasi ndani ya uso wa Gaussia wa mviringo wa radius r. Hii inatoa uhusiano zifuatazo kwa sheria Gauss:

\[4\pi r^2 E = \dfrac{q_{enc}}{\epsilon_0}.\]

Kwa hiyo, uwanja wa umeme katika hatua P ambayo ni umbali r kutoka katikati ya usambazaji wa malipo ya spherically symmetrical ina ukubwa na mwelekeo wafuatayo:

\[Magnitude: \, E(r) = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{enc}}{r^2}\]

Mwelekeo: radial kutoka O hadi P au kutoka P hadi O.

Mwelekeo wa shamba kwenye hatua P inategemea kama malipo katika nyanja ni chanya au hasi. Kwa malipo mazuri yaliyofungwa ndani ya uso wa Gaussia, mwelekeo unatoka O hadi P, na kwa malipo mabaya ya wavu, mwelekeo unatoka P hadi O. Hii ni yote tunahitaji kwa ajili ya malipo ya uhakika, na utagundua kwamba matokeo hapo juu ni sawa na kwamba kwa malipo uhakika. Hata hivyo, sheria ya Gauss inakuwa muhimu sana katika kesi ambapo malipo inachukua kiasi cha mwisho.

Computing iliyoambatanishwa malipo

Kesi ya kuvutia zaidi ni wakati usambazaji wa malipo ya spherical unachukua kiasi, na kuuliza nini uwanja wa umeme ndani ya usambazaji wa malipo ni hivyo inakuwa muhimu. Katika kesi hiyo, malipo yaliyofungwa inategemea umbali r wa uhakika wa shamba kuhusiana na eneo la usambazaji wa malipo R, kama vile ilivyoonyeshwa kwenye Kielelezo\(\PageIndex{3}\).

Kielelezo\(\PageIndex{3}\): usambazaji wa malipo ya spherically symmetrical na uso Gaussia kutumika kwa ajili ya kutafuta shamba (a) ndani na (b) nje ya usambazaji.

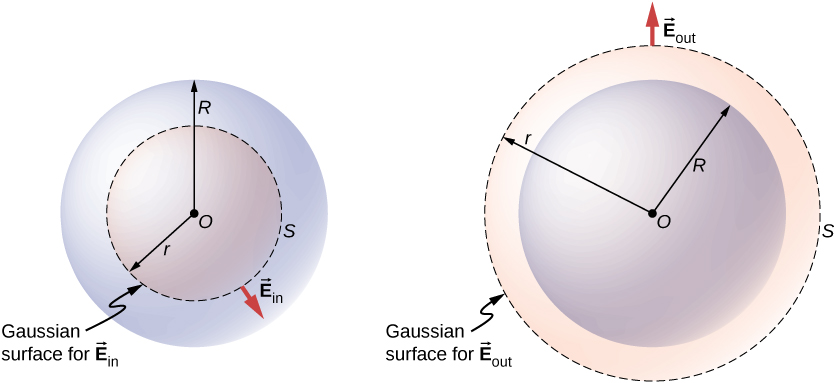
Ikiwa hatua P iko nje ya usambazaji wa malipo - yaani, ikiwa\(r \geq R\) - basi uso wa Gaussia ulio na P unahusisha mashtaka yote katika nyanja. Katika kesi hii,\(q_{enc}\) ni sawa na malipo ya jumla katika nyanja. Kwa upande mwingine, ikiwa hatua P iko ndani ya usambazaji wa malipo ya spherical, yaani, ikiwa\(r < R\), basi uso wa Gaussia unazunguka nyanja ndogo kuliko nyanja ya usambazaji wa malipo. Katika kesi hiyo,\(q_{enc}\) ni chini ya malipo ya jumla ya sasa katika nyanja. Akizungumzia Kielelezo\(\PageIndex{3}\), tunaweza kuandika\(q_{enc}\) kama

\[q_{enc} = q_{tot} (total \, charge) \, if \, r \geq R\]

\[q_{enc} = q_{within \, r < R} (only \, charge \, within \, r < R) \, if \, r < R\]

Shamba kwenye hatua nje ya usambazaji wa malipo huitwa pia\(\vec{E}_{out}\), na shamba kwenye hatua ndani ya usambazaji wa malipo huitwa\(\vec{E}_{in}\). Kuzingatia aina mbili za pointi za shamba, ama ndani au nje ya usambazaji wa malipo, sasa tunaweza kuandika ukubwa wa uwanja wa umeme kama

\[P \, outside \, sphere \, E_{out} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}}{r^2}\]

\[P \, inside \, sphere \, E_{in} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{within \, r < R}}{r^2}.\]

Kumbuka kuwa uwanja wa umeme nje ya usambazaji wa malipo ya spherically ulinganifu ni sawa na ile ya malipo ya uhakika katikati ambayo ina malipo sawa na malipo ya jumla ya usambazaji wa malipo ya spherical. Hii ni ya ajabu kwani mashtaka hayapo katikati tu. Sasa tunafanya mifano maalum ya mgawanyo wa malipo ya spherical, kuanzia na kesi ya nyanja ya kushtakiwa kwa usawa.

Sawa kushtakiwa nyanja

Aina ya radius R, kama ile iliyoonyeshwa kwenye Kielelezo\(\PageIndex{3}\), ina wiani wa malipo ya kiasi cha sare\(\rho_0\). Pata shamba la umeme kwenye hatua nje ya nyanja na kwa hatua ndani ya nyanja.

Mkakati

Tumia mkakati wa kutatua matatizo ya sheria ya Gauss, ambapo tumefanya kazi ya hesabu ya mtiririko.

Suluhisho

Malipo yaliyofungwa na uso wa Gaussia hutolewa na

\[q_{enc} = \int \rho_0 dV = \int_0^r \rho_0 4\pi r'^2 dr' = \rho \left(\dfrac{4}{3} \pi r^3\right).\]

Jibu la amplitude ya shamba la umeme linaweza kuandikwa mara moja kwa hatua nje ya nyanja, iliyoandikwa\(E_{out}\) na hatua ndani ya nyanja, iliyoandikwa\(E_{in}\).

\[E_{out} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}}{r^2}, \, q_{tot} = \dfrac{4}{3} \pi R^3 \, \rho_0,\]

\[E_{in} = \dfrac{q_{enc}}{4\pi \epsilon_0 r^2} = \dfrac{\rho_0r}{3 \epsilon_0}, \, since \, q_{enc} = \dfrac{4}{3} \pi r^3 \rho_0.\]

Inashangaza kutambua kwamba ukubwa wa shamba la umeme huongezeka ndani ya nyenzo unapoondoka, kwa kuwa kiasi cha malipo kilichofungwa na uso wa Gaussia kinaongezeka kwa kiasi. Hasa, malipo iliyoambatanishwa inakua\(\propto r^3\), wakati shamba kutoka kwa kila kipengele cha malipo cha chini cha matone\(\propto 1/r^2\) na matokeo halisi ambayo shamba la umeme ndani ya usambazaji huongezeka kwa nguvu linearly na radius. Ukubwa wa uwanja wa umeme nje ya nyanja hupungua unapoondoka kwenye mashtaka, kwa sababu malipo yaliyojumuishwa bado yanafanana lakini umbali unaongezeka. Kielelezo\(\PageIndex{4}\) kinaonyesha tofauti ya ukubwa wa uwanja wa umeme na umbali kutoka katikati ya nyanja ya kushtakiwa kwa usawa.

Kielelezo\(\PageIndex{4}\): Umeme shamba la kushtakiwa kwa usawa, usio na uendeshaji nyanja huongezeka ndani ya nyanja hadi kiwango cha juu kwenye uso na kisha hupungua kama\(1/r^2\). Hapa,\(E_R = \frac{\rho_0 R}{3 \epsilon_0}\). Shamba la umeme linatokana na usambazaji wa malipo ya spherical ya wiani wa malipo ya sare na malipo ya jumla Q kama kazi ya umbali kutoka katikati ya usambazaji.

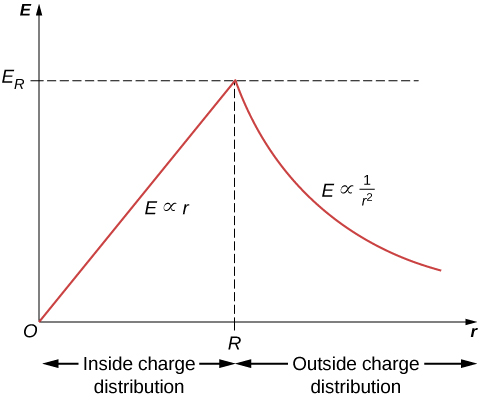
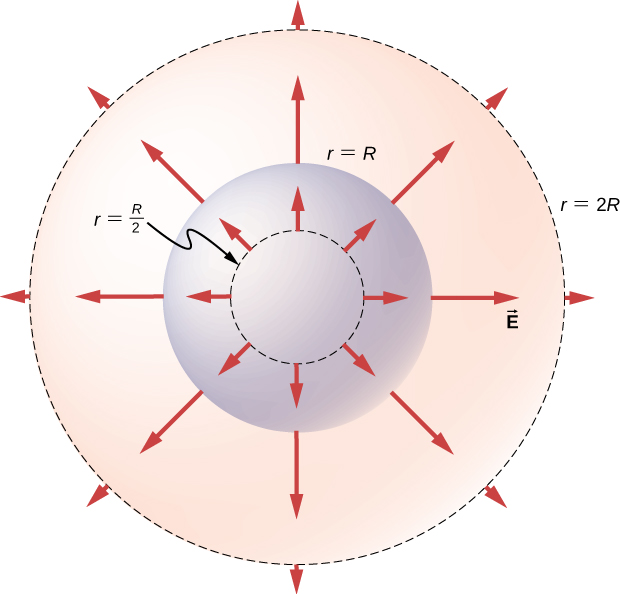
Mwelekeo wa uwanja wa umeme wakati wowote P ni radially nje kutoka asili ikiwa\(\rho_0\) ni chanya, na ndani (yaani, kuelekea katikati) ikiwa\(\rho_0\) ni hasi. uwanja umeme katika baadhi ya pointi mwakilishi nafasi ni kuonyeshwa katika Kielelezo\(\PageIndex{5}\) ambao radial kuratibu r ni\(r = R/2, \, r = R,\) na\(r = 2R\).

Kielelezo\(\PageIndex{5}\): Vectors ya shamba la umeme ndani na nje ya nyanja ya kushtakiwa kwa usawa.

Umuhimu

Taarifa ambayo\(E_{out}\) ina fomu sawa na equation ya uwanja wa umeme wa malipo ya pekee ya uhakika. Katika kuamua uwanja wa umeme wa usambazaji wa malipo ya sare ya spherical, tunaweza kudhani kwamba malipo yote ndani ya uso unaofaa wa Gaussia iko katikati ya usambazaji.

Zisizo Sawa kushtakiwa Sphere

Sehemu isiyo ya kufanya ya radius R ina wiani usio sare ya malipo ambayo inatofautiana na umbali kutoka katikati yake kama iliyotolewa na

\[\rho(r) = ar^n (r \leq R; \, n \geq 0), \nonumber\]

ambapo ni mara kwa mara. Tunahitaji\(n \geq 0\) ili wiani wa malipo haukufafanuliwa\(r = 0\). Pata shamba la umeme kwenye hatua nje ya nyanja na kwa hatua ndani ya nyanja.

Mkakati

Tumia mkakati wa sheria wa Gauss uliotolewa hapo juu, ambapo tunafanya kazi nje ya integrals malipo iliyoambatanishwa tofauti kwa kesi ndani na nje ya nyanja.

Suluhisho

Kwa kuwa kutokana malipo wiani kazi ina tu utegemezi radial na hakuna utegemezi juu ya mwelekeo, tuna spherically symmetrical hali. Kwa hiyo, ukubwa wa shamba la umeme wakati wowote hutolewa hapo juu na mwelekeo ni radial. Tunahitaji tu kupata malipo yaliyofungwa\(q_{enc}\), ambayo inategemea eneo la uhakika wa shamba.

Maelezo kuhusu alama: Tunatumia\(r'\) kwa ajili ya kupata mashtaka katika usambazaji wa malipo na r kwa kupata uhakika wa shamba (s) kwenye uso wa Gaussia. Barua R hutumiwa kwa radius ya usambazaji wa malipo.

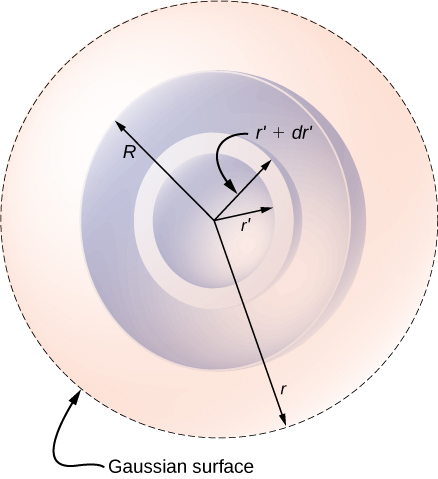
Kama wiani wa malipo sio mara kwa mara hapa, tunahitaji kuunganisha kazi ya wiani wa malipo juu ya kiasi kilichofungwa na uso wa Gaussia. Kwa hiyo, sisi kuanzisha tatizo kwa mashtaka katika shell moja spherical, kusema kati\(r'\) na\(r' + dr'\) kama inavyoonekana katika Kielelezo\(\PageIndex{6}\). Kiasi cha mashtaka katika shell ya upana usio na kipimo ni sawa na bidhaa ya eneo la uso\(4\pi r'^2\) na unene\(dr'\). Kuzidisha kiasi na wiani katika eneo hili\(ar'^n\), yaani, hutoa malipo katika shell:

\[dq = ar'^n 4\pi r'^2 dr'. \nonumber\]

Kielelezo\(\PageIndex{6}\): Ulinganifu wa spherical na usambazaji wa malipo yasiyo ya sare. Katika aina hii ya tatizo, tunahitaji radii nne: R ni radius ya usambazaji wa malipo, r ni radius ya uso wa Gaussia,\(r'\) ni radius ya ndani ya shell ya spherical, na\(r' + dr'\) ni radius ya nje ya shell ya spherical. Hifadhi ya spherical hutumiwa kuhesabu malipo yaliyofungwa ndani ya uso wa Gaussia. Aina ya\(r'\) ni kutoka 0 hadi r kwa shamba kwa uhakika ndani ya usambazaji wa malipo na kutoka 0 hadi R kwa shamba kwa uhakika nje ya usambazaji wa malipo. Ikiwa\(r > R\), basi uso wa Gaussia unafunga kiasi zaidi kuliko usambazaji wa malipo, lakini kiasi cha ziada hakichangia\(q_{enc}\).

(a) Field katika hatua nje ya usambazaji malipo. Katika kesi hiyo, uso wa Gaussia, ambao una uhakika wa shamba P, una r radius ambayo ni kubwa kuliko radius R ya usambazaji wa malipo,\(r > R\). Kwa hiyo, mashtaka yote ya usambazaji wa malipo yanafungwa ndani ya uso wa Gaussia. Kumbuka kuwa nafasi kati\(r' = R\) na\(r' = r\) ni tupu ya mashtaka na kwa hiyo haina kuchangia muhimu juu ya kiasi kilichofungwa na uso wa Gaussia:

\[q_{enc} = \int dq = \int_0^R ar'^n 4\pi r'^2 dr' = \dfrac{4\pi a}{n + 3} R^{n+3}. \nonumber\]

Hii hutumiwa kwa matokeo ya jumla kwa\(E_{out}\) hapo juu ili kupata uwanja wa umeme kwa hatua nje ya usambazaji wa malipo kama

\[ \vec{E}_{out} = \left[ \dfrac{aR^{n+3}}{\epsilon_0(n + 3)} \right] \dfrac{1}{r^2} \hat{r}, \nonumber\]

\(\hat{r}\)wapi vector kitengo katika mwelekeo kutoka asili hadi hatua ya shamba kwenye uso wa Gaussia.

(b) Field katika hatua ndani ya usambazaji malipo. Uso wa Gaussia sasa umezikwa ndani ya usambazaji wa malipo, na\(r < R\). Kwa hiyo, mashtaka hayo tu katika usambazaji ambao ni ndani ya umbali r katikati ya usambazaji wa malipo ya spherical kuhesabu katika\(r_{enc}\):

\[q_{enc} = \int_0^r ar'^n 4\pi r'^2 dr' = \dfrac{4\pi a}{n + 3} r^{n+3}. \nonumber\]

Sasa, kwa kutumia matokeo ya jumla hapo juu kwa\(\vec{E}_{in}\), tunapata shamba la umeme kwenye hatua ambayo ni umbali r kutoka katikati na uongo ndani ya usambazaji wa malipo kama

\[\vec{E}_{in} = \left[ \dfrac{a}{\epsilon_0 ( n + 3)} \right] r^{n+1} \hat{r}, \nonumber\]

ambapo taarifa ya mwelekeo ni pamoja na kwa kutumia kitengo radial vector.

Zoezi\(\PageIndex{1}\)

Angalia kwamba mashamba ya umeme kwa nyanja hupunguza maadili sahihi kwa malipo ya uhakika.

Suluhisho

Katika kesi hii, kuna tu\(\vec{E}_{out}\). Kwa hiyo, ndiyo.

Usambazaji wa malipo na ulinganifu wa Cylindr

Usambazaji wa malipo una ulinganifu wa cylindrical ikiwa wiani wa malipo unategemea tu umbali r kutoka mhimili wa silinda na haipaswi kutofautiana pamoja na mhimili au kwa mwelekeo kuhusu mhimili. Kwa maneno mengine, ikiwa mfumo wako unatofautiana ikiwa unazunguka karibu na mhimili, au ukiibadilisha kando ya mhimili, huna ulinganifu wa cylindrical.

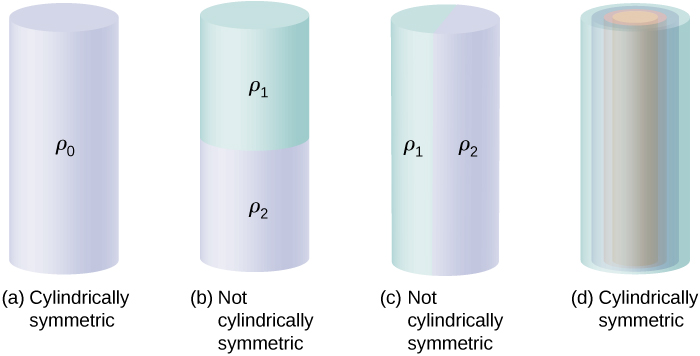
Kielelezo\(\PageIndex{7}\) kinaonyesha hali nne ambazo mashtaka yanasambazwa katika silinda. Uzito wa malipo ya sare\(\rho_0\) katika waya usio na kipimo una ulinganifu wa cylindrical, na hivyo silinda kubwa ya muda mrefu na wiani wa malipo ya mara kwa mara\(\rho_0\). Silinda isiyo na mwisho ambayo ina densities tofauti ya malipo kwa urefu wake, kama wiani wa malipo kwa\(z > 0\) na\(\rho_1\)\(\rho_2 \neq \rho_1\) kwa\(z < 0\), haina ulinganifu wa cylindrical unaoweza kutumika kwa kozi hii. Wala haina silinda ambayo malipo wiani inatofautiana na mwelekeo, kama vile wiani malipo\(\rho_1\) kwa\(0 \leq \theta < \pi\) na\(\rho_2 \neq \rho_1\) kwa\(\pi \leq \theta < 2\pi\). Mfumo wenye makombora ya cylindrical ya makini, kila mmoja na densities ya malipo ya sare, ingawa tofauti katika shells tofauti, kama katika FiFigure\(\PageIndex{7d}\), ina ulinganifu wa cylindrical ikiwa ni mrefu sana. Mahitaji ya urefu usio na kipimo ni kutokana na wiani wa malipo unaobadilika kwenye mhimili wa silinda ya mwisho. Katika mifumo halisi, hatuna mitungi usio; Hata hivyo, kama kitu cha cylindrical ni kikubwa zaidi kuliko radius kutoka kwao kwamba tuna nia ya, basi makadirio ya silinda isiyo na kipimo inakuwa muhimu.

Kielelezo\(\PageIndex{7}\): Kuamua kama usambazaji wa malipo unaopewa una ulinganifu wa cylindrical, angalia sehemu ya msalaba wa silinda “isiyo na muda mrefu”. Ikiwa wiani wa malipo hautegemei angle ya polar ya sehemu ya msalaba au kando ya mhimili, basi una ulinganifu wa cylindrical. (a) Wiani wa malipo ni mara kwa mara katika silinda; (b) nusu ya juu ya silinda ina wiani tofauti wa malipo kutoka nusu ya chini; (c) nusu ya kushoto ya silinda ina wiani tofauti wa malipo kutoka nusu sahihi; (d) mashtaka ni mara kwa mara katika pete tofauti za cylindrical, lakini wiani hautegemei polar pembe. Kesi (a) na (d) zina ulinganifu wa cylindrical, ambapo (b) na (c) hawana.

Matokeo ya Saymmetry

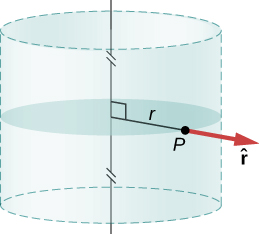
Katika kesi zote za cylindrically symmetrical, uwanja wa umeme\(E_p\) wakati wowote\(P\) lazima pia kuonyesha ulinganifu wa cylindrical.

Ulinganifu wa cylindrical:\(\vec{E}_p = E_p(r)\hat{r}\), wapi\(r\) umbali kutoka kwa mhimili na\(\hat{r}\) ni vector ya kitengo iliyoongozwa perpendicularly mbali na mhimili (Kielelezo\(\PageIndex{8}\)).

Kielelezo\(\PageIndex{8}\): Shamba la umeme katika hali ya cylindrically symmetrical inategemea tu umbali kutoka kwa mhimili. Mwelekeo wa uwanja wa umeme umeelezwa mbali na mhimili kwa mashtaka mazuri na kuelekea mhimili kwa mashtaka hasi.

Gaussia uso na hesabu ya mtiririko

Ili kutumia mwelekeo na utegemezi wa kazi wa uwanja wa umeme, tunachagua uso wa Gaussia uliofungwa kwa sura ya silinda na mhimili sawa na mhimili wa usambazaji wa malipo. Flux kupitia uso huu wa radius s na urefu L ni rahisi kuhesabu kama sisi kugawanya kazi yetu katika sehemu mbili: (a) flux kupitia mwisho gorofa na (b) flux kupitia uso curved (Kielelezo\(\PageIndex{9}\)).

Kielelezo\(\PageIndex{9}\): Uso wa Gaussia katika kesi ya ulinganifu wa cylindrical. Shamba la umeme kwenye kiraka ni sambamba au perpendicular kwa kawaida kwa kiraka cha uso wa Gaussia.

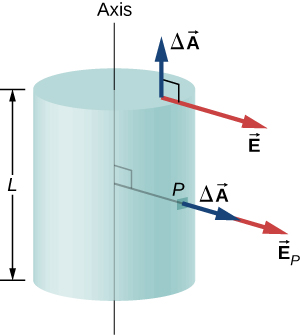
Shamba la umeme ni perpendicular kwa upande wa cylindrical na sambamba na kofia za mwisho za uso. Flux kupitia sehemu ya cylindrical ni

\[\int_S \vec{E} \cdot \hat{n} dA = E \int_S dA = E(2\pi r L), \nonumber\]

ambapo flux kupitia kofia mwisho ni sifuri kwa sababu\(\vec{E} \cdot \hat{n} = 0\) kuna. Hivyo, flux ni

\[\int_S \vec{E} \cdot \hat{n} dA = E(2\pi rL) + 0 + 0 = 2\pi rLE. \nonumber\]

Kutumia sheria ya Gauss

Kwa mujibu wa sheria ya Gauss, mtiririko lazima ufanane na kiasi cha malipo ndani ya kiasi kilichofungwa na uso huu, umegawanyika na permittivity ya nafasi ya bure. Unapofanya hesabu kwa silinda ya urefu L, unakuta ile\(q_{enc}\) ya sheria ya Gauss ni moja kwa moja sawia na L. Hebu kuandika kama malipo kwa kitengo urefu (\(\lambda_{enc}\)) mara urefu L:

\[q_{enc} = \lambda_{enc} L.\]

Kwa hiyo, sheria ya Gauss kwa usambazaji wowote wa malipo ya cylindrically hutoa ukubwa wafuatayo wa uwanja wa umeme umbali s mbali na mhimili:

\[Magnitude: \, E(r) = \dfrac{\lambda_{enc}}{2\pi \epsilon_0} \dfrac{1}{r}.\]

Malipo kwa urefu wa kitengo\(\lambda_{enc}\) inategemea kama hatua ya shamba iko ndani au nje ya silinda ya usambazaji wa malipo, kama tulivyoona kwa usambazaji wa spherical.

Computing iliyoambatanishwa malipo

Hebu R iwe radius ya silinda ndani ambayo mashtaka yanasambazwa kwa njia ya cylindrically symmetrical. Hebu shamba uhakika P kuwa katika umbali s kutoka mhimili. (Upande wa uso wa Gaussia unajumuisha hatua ya shamba P.) Wakati\(r > R\) (yaani, wakati P iko nje ya usambazaji wa malipo), uso wa Gaussia unajumuisha malipo yote katika silinda ya radius R na urefu L. Wakati\(r < R\) (P iko ndani ya usambazaji wa malipo), basi malipo tu ndani ya silinda ya radius s na urefu L imefungwa na uso wa Gaussia:

\(\lambda_{enc} = (total \, charge) \, if \, r \geq R\)

\(\lambda_{enc} = (only \, charge \, within \, t < R) \, if \, r < R\)

Sawa kushtakiwa Silinda Shell

Muda mrefu sana usio na conductive cylindrical shell ya radius R ina sare uso malipo wiani\(\sigma_0\) Kupata shamba umeme (a) katika hatua nje ya shell na (b) katika hatua ndani ya shell.

Mkakati

Tumia mkakati wa sheria wa Gauss uliotolewa hapo awali, ambapo tunashughulikia kesi ndani na nje ya shell tofauti.

Suluhisho

uwanja wa umeme kwa hatua nje ya shell. Kwa hatua nje ya shell ya cylindrical, uso wa Gaussia ni uso wa silinda ya radius\(r > R\) na urefu L, kama inavyoonekana kwenye Mchoro\(\PageIndex{10}\). Malipo yaliyofungwa na silinda ya Gaussia ni sawa na malipo kwenye shell ya cylindrical ya urefu L. Kwa hiyo,\(\lambda_{enc}\) ni iliyotolewa na\[\lambda_{enc} = \dfrac{\sigma_0 2\pi RL}{L} = 2\pi R \sigma_0.\]

Kielelezo\(\PageIndex{10}\): uso wa Gaussia unaozunguka shell ya cylindrical.

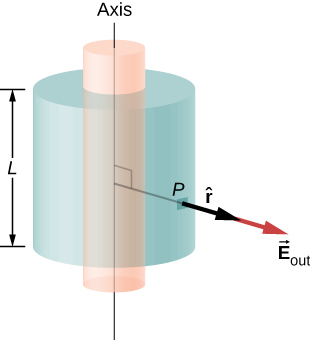
Kwa hiyo, uwanja wa umeme kwenye hatua P nje ya shell kwa mbali r mbali na mhimili ni

\[\vec{E} = \dfrac{2\pi R \sigma_0}{2 \pi \epsilon_0} \dfrac{1}{r} \hat{r} = \dfrac{R\sigma_0}{\epsilon_0} \dfrac{1}{r} \hat{r} \, (r > R)\]

wapi\(\hat{r}\) vector kitengo, perpendicular kwa mhimili na akizungumzia mbali nayo, kama inavyoonekana katika takwimu. uwanja umeme katika P pointi katika mwelekeo wa\(\hat{r}\) kutolewa katika Kielelezo\(\PageIndex{10}\) kama\(\sigma_0 > 0\) na katika mwelekeo kinyume na\(\hat{r}\) kama\(\sigma_0 <0\).

b Umeme shamba katika hatua ndani ya shell. Kwa hatua ndani ya shell ya cylindrical, uso wa Gaussia ni silinda ambayo radius r ni chini ya R (Kielelezo\(\PageIndex{11}\)). Hii inamaanisha hakuna mashtaka yanayojumuishwa ndani ya uso wa Gaussia:

\[\lambda_{enc} = 0.\]

Kielelezo\(\PageIndex{11}\): Uso wa Gaussia ndani ya shell ya cylindrical.

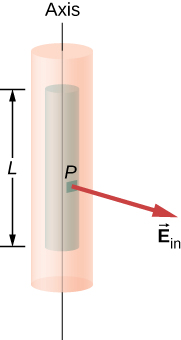
Hii inatoa equation ifuatayo kwa ukubwa wa uwanja wa umeme kwa\(E_{in}\) hatua ambayo r ni chini ya R ya shell ya mashtaka.

\[E_{in} 2\pi rL = 0 (r<R), \nonumber\]

Hii inatupa

\[E_{in} = 0 (r < R). \nonumber\]

Umuhimu

Kumbuka kwamba matokeo ndani ya shell ni nini hasa tunapaswa kutarajia: Hakuna malipo iliyoambatanishwa ina maana zero uwanja umeme. Nje ya shell, matokeo inakuwa sawa na waya na malipo sare\(R\sigma\).

Zoezi\(\PageIndex{2}\)

Waya nyembamba moja kwa moja ina wiani wa malipo ya mstari wa sare\(\lambda_0\). Pata shamba la umeme umbali d kutoka waya, ambapo d ni chini sana kuliko urefu wa waya.

Suluhisho

\(\vec{E} = \frac{\lambda_0}{2\pi \epsilon_0} \frac{1}{d} \hat{r}\); Hii inakubaliana na hesabu ya [kiungo] ambapo tulipata shamba la umeme kwa kuunganisha juu ya waya iliyoshtakiwa. Angalia jinsi rahisi hesabu ya uwanja huu wa umeme ni pamoja na sheria ya Gauss.

Usambazaji wa Malipo na Ulinganifu wa Planar

Ulinganifu wa mpango wa wiani wa malipo hupatikana wakati mashtaka yanaenea kwa usawa juu ya uso mkubwa wa gorofa. Katika ulinganifu wa mpango, pointi zote katika ndege sambamba na ndege ya malipo zinafanana na heshima na mashtaka.

Matokeo ya ulinganifu

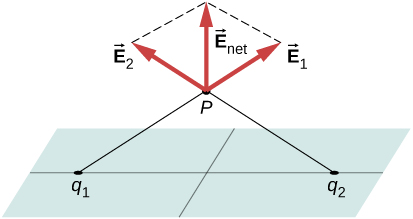
Tunachukua ndege ya usambazaji wa malipo kuwa xy -ndege na tunapata uwanja wa umeme kwenye hatua ya nafasi P na kuratibu (x, y, z). Kwa kuwa wiani wa malipo ni sawa kabisa (x, y) -kuratibu katika\(z = 0\) ndege, kwa ulinganifu, uwanja wa umeme katika P hauwezi kutegemea x - au y -kuratibu ya uhakika P, kama inavyoonekana kwenye Kielelezo\(\PageIndex{12}\). Kwa hiyo, uwanja wa umeme katika P unaweza tu kutegemea umbali kutoka ndege na ina mwelekeo ama kuelekea ndege au mbali na ndege. Hiyo ni, shamba la umeme katika P lina tu sehemu isiyo ya zero z.

Mashtaka sare katika xy ndege:\(\vec{E} = E(z) \hat{z}\) ambapo z ni umbali kutoka ndege na\(\hat{z}\) ni kitengo vector kawaida kwa ndege. Kumbuka kuwa katika mfumo huu\(E(z) = E(-z)\), ingawa bila shaka wanaelezea kwa njia tofauti.

Kielelezo\(\PageIndex{12}\): Vipengele vya uwanja wa umeme vinavyolingana na ndege ya mashtaka kufuta mashtaka mawili yaliyo sawa na hatua ya shamba P. Kwa hiyo, shamba wakati wowote linaelekezwa kwa wima kutoka ndege ya mashtaka. Kwa hatua yoyote P na malipo\(q_1\), tunaweza daima kupata\(q_2\) na athari hii.

Gaussia uso na hesabu ya mtiririko

Katika kesi ya sasa, uso rahisi wa Gaussia ni sanduku, kwani uwanja wa umeme unaotarajiwa unaonyesha mwelekeo mmoja tu. Ili kuweka sanduku la Gaussia linganifu juu ya ndege ya mashtaka, tunachukua ili kuondokana na ndege ya mashtaka, kama vile uso mmoja ulio na hatua ya shamba P inachukuliwa sambamba na ndege ya mashtaka. Katika Mchoro\(\PageIndex{13}\), pande I na II za uso wa Gaussia (sanduku) ambazo ni sawa na ndege isiyo na mwisho zimekuwa kivuli. Wao ni nyuso pekee zinazoongezeka kwa nonzero flux kwa sababu uwanja wa umeme na vectors eneo la nyuso nyingine ni perpendicular kwa kila mmoja.

Kielelezo\(\PageIndex{13}\): Karatasi nyembamba ya kushtakiwa na sanduku la Gaussia kwa kutafuta uwanja wa umeme kwenye hatua ya shamba P. Kawaida kwa kila uso wa sanduku ni kutoka ndani ya sanduku kwenda nje. Katika nyuso mbili za sanduku, mashamba ya umeme yanafanana na vectors ya eneo hilo, na kwenye nyuso nyingine nne, mashamba ya umeme yanapatikana kwa vectors eneo hilo.

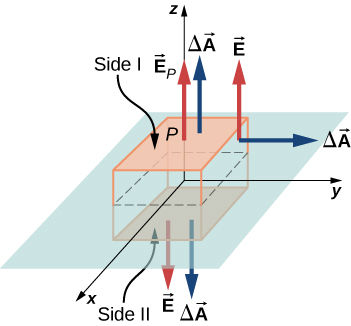
Hebu A kuwa eneo la uso kivuli kila upande wa ndege na E P.

kuwa ukubwa wa uwanja wa umeme katika hatua P. Kwa kuwa pande I na II ni umbali sawa na ndege, uwanja wa umeme una ukubwa sawa katika pointi katika ndege hizi, ingawa maelekezo ya uwanja wa umeme katika pointi hizi katika ndege mbili ni kinyume na kila mmoja.

Ukubwa katika I au II:\(E(z) = E_p\).

Ikiwa malipo kwenye ndege ni chanya, basi mwelekeo wa uwanja wa umeme na vectors eneo ni kama inavyoonekana kwenye Mchoro\(\PageIndex{13}\). Kwa hiyo, tunapata kwa mtiririko wa shamba la umeme kupitia sanduku

\[\Phi = \int_S \vec{E}_p \cdot \hat{n} dA = E_pA + E_pA + 0 + 0 + 0 + 0 = 2E_p A\]

ambapo zero ni kwa ajili ya kuenea kwa njia ya pande nyingine za sanduku. Kumbuka kwamba ikiwa malipo kwenye ndege ni hasi, maelekezo ya uwanja wa umeme na vectors eneo kwa ndege I na II ni kinyume na kila mmoja, na tunapata ishara hasi kwa kuongezeka. Kwa mujibu wa sheria ya Gauss, flux lazima iwe sawa\(q_{enc}/\epsilon_0\). Kutoka Kielelezo\(\PageIndex{13}\), tunaona kwamba mashtaka ndani ya kiasi iliyoambatanishwa na sanduku Gaussia wanaishi katika eneo A ya xy -plane. Hivyo,

\[q_{enc} = \sigma_0 A. \nonumber\]

Kutumia equations kwa malipo ya mtiririko na yaliyofungwa katika sheria ya Gauss, tunaweza kuamua mara moja uwanja wa umeme kwa hatua ya urefu z kutoka ndege iliyoshtakiwa kwa usawa katika xy -plane:

\[\vec{E}_p = \dfrac{\sigma_0}{2\epsilon_0} \hat{n}. \nonumber\]

Mwelekeo wa shamba unategemea ishara ya malipo kwenye ndege na upande wa ndege ambapo hatua ya shamba P iko. Kumbuka kuwa juu ya ndege,\(\hat{n} = + \hat{z}\), wakati chini ya ndege,\(\hat{n} = - \hat{z}\).

Unaweza kushangaa kutambua kwamba shamba la umeme halitegemei umbali kutoka ndege; hii ni athari ya dhana kwamba ndege haina mwisho. Kwa maneno ya vitendo, matokeo yaliyotolewa hapo juu bado ni makadirio muhimu kwa ndege za mwisho karibu na kituo.