5.9: Kiasi cha Uhusiano

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Kufafanua kasi relativistic katika suala la wingi na kasi
• Onyesha jinsi relativistic kasi inahusiana na kasi classical
• Onyesha jinsi uhifadhi wa relativistic kasi mipaka vitu na wingi kwa kasi chini ya c

Kasi ni dhana kuu katika fizikia. Aina pana zaidi ya sheria ya pili ya Newton imesemwa kwa suala la kasi. Momentum ni kuhifadhiwa wakati wowote wavu nje nguvu juu ya mfumo ni sifuri. Hii inafanya uhifadhi wa kasi chombo cha msingi cha kuchambua migongano (Kielelezo\(\PageIndex{1}\)). Mengi ya kile tunachokijua kuhusu muundo wa subatomic linatokana na uchambuzi wa migongano ya chembe za relativistic zinazozalishwa na kasi, na uhifadhi wa kasi una jukumu muhimu katika uchambuzi huu.

Kielelezo\(\PageIndex{1}\): Momentum ni dhana muhimu kwa wachezaji hawa wa soka kutoka Chuo Kikuu cha California katika Berkeley na Chuo Kikuu cha California huko Davis Mchezaji mwenye kasi sawa lakini molekuli kubwa hugongana na athari kubwa kwa sababu kasi yake ni kubwa zaidi. Kwa vitu vinavyohamia kwa kasi ya relativistic, athari ni kubwa zaidi.

Postulate ya kwanza ya relativity inasema kwamba sheria za fizikia ni sawa katika muafaka wote wa inertial. Je, sheria ya uhifadhi wa kasi huishi mahitaji haya kwa kasi ya juu? Inaweza kuonyeshwa kuwa kasi iliyohesabiwa kama tu\(\vec{p} = m\frac{d\vec{x}}{dt}\), hata ikiwa imehifadhiwa katika sura moja ya kumbukumbu, haiwezi kuhifadhiwa katika mwingine baada ya kutumia mabadiliko ya Lorentz kwa kasi. Equation sahihi kwa kasi inaweza kuonyeshwa, badala yake, kuwa kujieleza classical katika suala la nyongeza dya muda mzuri wa chembe, aliona katika sura ya mapumziko ya chembe:

\[\begin{align*} \vec{p} &= m\frac{d\vec{x}}{dτ} = m\frac{d\vec{x}}{dt} \frac{dt}{d\tau} \\[5pt] &= m\frac{d\vec{x}}{dt}\frac{1}{\sqrt{1 - u^2/c^2}} \\[5pt] &= \frac{m\vec{u}}{\sqrt{1 - u^2/c^2}} \\[5pt] &= \gamma m\vec{u}.\end{align*} \nonumber \]

Ufafanuzi: Relativistic Kasi na kupumzika Misa

Kasi ya relativistic\(\vec{p}\) ni kasi ya kawaida inayoongezeka kwa sababu ya relativistic\(\gamma\):

\[\vec{p} = \gamma m\vec{u} \label{Rmomentum} \]

wapi\(m\) wingi wa kitu,\(\vec{u}\) ni kasi yake kuhusiana na mwangalizi, na\(γ\) ni sababu ya relativistic:

\[\gamma = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}. \label{Rmass} \]

Kumbuka kwamba tunatumia\(u\) kwa kasi hapa ili kuitofautisha kutoka kwa kasi ya jamaa\(v\) kati ya waangalizi. Sababu\(\gamma\) inayotokea hapa ina umbo sawa na sababu ya awali ya relativistic\(\gamma\) isipokuwa kwamba sasa iko katika suala la kasi ya chembe\(u\) badala ya kasi ya jamaa v ya muafaka mbili za kumbukumbu.

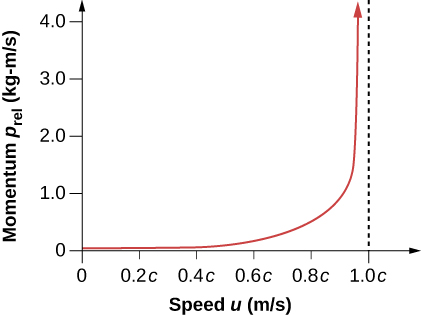
Kwa p walionyesha kwa njia hii, jumla ya kasi\(p_{tot}\) ni kuhifadhiwa wakati wowote wavu nje nguvu ni sifuri, kama katika fizikia classical. Tena tunaona kwamba kiasi relativistic inakuwa karibu sawa na wingi classical katika kasi ya chini, ambapo\(u/c\) ni ndogo na\(\gamma\) ni karibu sana sawa na 1. Relativistic kasi ina jukumu sawa angavu kama kasi classical. Ni kubwa kwa raia kubwa kusonga kwa kasi ya juu, lakini kwa sababu ya sababu, kasi ya relativistic inakaribia infinity kama\(u\) mbinu\(c\) (Kielelezo\(\PageIndex{2}\)).\(\gamma\) Hii ni dalili nyingine ya kwamba kitu kilicho na masi hakiwezi kufikia kasi ya nuru. Kama alifanya hivyo, kasi yake itakuwa infinite-thamani isiyo na maana.

Kielelezo\(\PageIndex{2}\): Relativistic kasi inakaribia infinity kama kasi ya kitu inakaribia kasi ya mwanga.

Misa dhidi ya kupumzika molekuli

Ufafanuzi wa relativistically sahihi wa kasi (Equation\ ref {Rmomentum}) wakati mwingine huchukuliwa ili kuashiria kwamba molekuli inatofautiana na kasi:\(m_{var} = \gamma m\), hasa katika vitabu vya zamani. Hata hivyo, kumbuka kwamba\(m\) ni wingi wa kitu kama kipimo na mtu katika mapumziko jamaa na kitu. Hivyo,\(m\) hufafanuliwa kuwa molekuli wengine, ambayo inaweza kupimwa wakati wa kupumzika, labda kwa kutumia mvuto. Wakati wingi unahamia jamaa na mwangalizi, njia pekee ambayo umati wake unaweza kuamua ni kupitia migongano au njia nyingine zinazohusisha kasi. Kwa sababu umati wa kitu cha kusonga hawezi kuamua kwa kujitegemea kwa kasi, molekuli pekee yenye maana ni kupumzika kwa wingi. Kwa hiyo, tunapotumia neno “wingi,” tunadhani kuwa sawa na “kupumzika kwa wingi.”

Kasi ya relativistic inaelezwa kwa namna ambayo uhifadhi wa kasi unashikilia katika muafaka wote wa inertial. Wakati wowote nguvu ya nje ya mfumo ni sifuri, kasi ya relativistic imehifadhiwa, kama ilivyo kwa kasi ya kawaida. Hii imethibitishwa katika majaribio mengi.

Zoezi\(\PageIndex{1}\)

Je! Ni kasi gani ya elektroni inayosafiri kwa kasi\(0.985c\)? Masi mengine ya elektroni ni\(9.11 \times 10^{-31} kg\).

Jibu

Badilisha data katika Equation\ ref {Rmomentum}:

\[\begin{align*} p &= \gamma mu \\[5pt] &= \frac{mu}{\sqrt{1 - \frac{u^2}{c^2}}} \\[5pt] &= \frac{(9.11 \times 10^{-31}kg)(0.985)(3.00 \times 10^8 \, m/s)}{\sqrt{1 - \frac{(0.985c)^2}{c^2}}} \\[5pt] &= 1.56 \times 10^{-21} \, kg-m/s. \end{align*} \nonumber \]