Skip to main content
Global

5.8: Athari ya Doppler kwa Mwanga

  1. Last updated
  2. Save as PDF
  • Page ID
    175493

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Eleza asili ya mabadiliko katika mzunguko na wavelength ya wavelength aliona wakati waangalizi na chanzo wakiongozwa kuelekea au mbali na kila mmoja
    • Pata kujieleza kwa mabadiliko ya Doppler ya relativistic
    • Tumia milinganyo ya mabadiliko ya Doppler kwa mifano halisi ya ulimwengu

    Kama ilivyojadiliwa katika sura ya sauti, ikiwa chanzo cha sauti na msikilizaji wanahamia mbali zaidi, msikilizaji hukutana na mzunguko mdogo wa wimbi katika kila pili, na kwa hiyo mzunguko wa chini, kuliko kama kujitenga kwao kunaendelea mara kwa mara. Kwa sababu hiyo hiyo, msikilizaji hutambua mzunguko wa juu ikiwa chanzo na msikilizaji wanakaribia. Mabadiliko ya Doppler yanayotokana na mzunguko unaogunduliwa hutokea kwa aina yoyote ya wimbi. Kwa mawimbi ya sauti, hata hivyo, equations kwa mabadiliko ya Doppler hutofautiana sana kulingana na kama ni chanzo, mwangalizi, au hewa, ambayo inahamia. Mwanga hauhitaji kati, na mabadiliko ya Doppler kwa mwanga kusafiri katika utupu inategemea tu kasi ya jamaa ya mwangalizi na chanzo.

    Athari ya Doppler Relativistic

    Tuseme mwangalizi katika\(S\) anaona mwanga kutoka chanzo katika\(S'\) kusonga mbali kwa kasi\(v\) (Kielelezo\(\PageIndex{1}\)). Urefu wa nuru unaweza kupimwa ndani\(S'\) — kwa mfano, kwa kutumia kioo kuanzisha mawimbi yaliyosimama na kupima umbali kati ya nodes. Umbali huu ni urefu sahihi na\(S'\) kama sura yao ya kupumzika, na mabadiliko kwa sababu\(\sqrt{1 - v^2/c^2}\) wakati kipimo katika sura ya mwangalizi\(S\), ambapo mtawala kupima wavelength katika\(S'\) inaonekana kama kusonga.

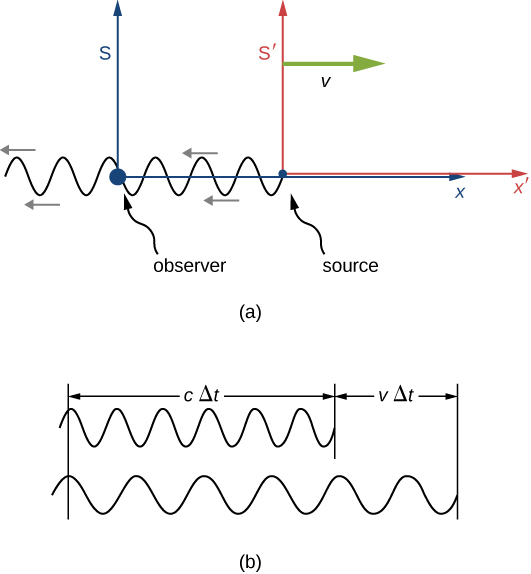
    Katika takwimu a: Mwangalizi ni inavyoonekana katika asili ya sura stationary S. sura S mkuu ni kusonga kwa haki na kasi v jamaa frame S. chanzo katika asili ya S mkuu inavyoonekana kutotoa wimbi sinusoidal kwamba kueneza kwa upande wa kushoto. Katika takwimu b, mzunguko sita wa wimbi huonyeshwa kama inavyoonekana na mwangalizi na kama inavyoonekana na chanzo. Urefu wa wimbi lililoonekana na mwangalizi ni mrefu kuliko ule wa wimbi lililoonekana na chanzo. upana wa mzunguko sita kama inavyoonekana na chanzo ni kinachoitwa kama c delta t. urefu wa ziada hadi mwisho wa mzunguko sita kama inavyoonekana na mwangalizi ni kinachoitwa kama v delta t.
    Kielelezo\(\PageIndex{1}\): (a) Wakati wimbi la mwanga linatolewa na chanzo kilichowekwa katika sura ya inertial inayohamia S', mwangalizi katika S anaona wavelength kipimo katika S'. kuwa mfupi kwa sababu\(\sqrt{1 - v^2/c^2}\). (b) Kwa sababu mwangalizi anaona chanzo kinachoondoka ndani ya S, muundo wa wimbi unaofikia mwangalizi katika S pia umewekwa na sababu\((c\Delta t + v\Delta t)/(c\Delta t) = 1 + v/c\).

    Ikiwa chanzo kilikuwa kimesimama katika S, mwangalizi angeona urefu wa muundo wa wimbi kwa wakati Δt. Lakini kwa sababu ya mwendo wa S' jamaa na S, kuchukuliwa tu ndani ya S, mwangalizi anaona muundo wa wimbi, na kwa hiyo wavelength, aliweka kwa sababu ya

    \[\frac{c\Delta t_{period} + v\Delta t_{period}}{c\Delta t_{period}} = 1 + \frac{v}{c} \nonumber \]

    kama mfano katika (b) ya Kielelezo\(\PageIndex{1}\). Ongezeko la jumla kutokana na athari zote mbili hutoa

    \[\begin{align*} \lambda_{obs} &= \lambda_{src} \left(1 + \frac{v}{c}\right) \sqrt{\frac{1}{1 - \frac{v^2}{c^2}}} \\[4pt] &= \lambda_{src} \left(1 + \frac{v}{c}\right) \sqrt{\frac{1}{\left(1 + \frac{v}{c}\right) \left(1 - \frac{v}{c}\right)}} \\[4pt] &= \lambda_{src}\sqrt{\frac{\left(1 + \frac{v}{c}\right)}{\left(1 - \frac{v}{c}\right)}} \end{align*} \nonumber \]

    \(\lambda_{src}\)wapi wavelength ya mwanga inayoonekana na chanzo katika S' na\(\lambda_{obs}\) ni wavelength ambayo mwangalizi hutambua ndani ya S.

    Mabadiliko nyekundu na Mabadiliko ya Bluu

    Wavelength iliyoonekana\(λ_{obs}\) ya mionzi ya sumakuumeme ni ndefu (inayoitwa “mabadiliko nyekundu”) kuliko ile iliyotolewa na chanzo wakati chanzo kinapoondoka mbali na mwangalizi. Vile vile, wavelength ni mfupi (inayoitwa “mabadiliko ya bluu”) wakati chanzo kinaendelea kuelekea mwangalizi. Kiasi cha mabadiliko kinatambuliwa na

    \[\lambda_{obs} = \lambda_s \sqrt{\frac{\left(1 + \frac{v}{c}\right)}{\left(1 - \frac{v}{c}\right)}} \nonumber \]

    \(\lambda_s\)wapi wavelength katika sura ya kumbukumbu ya chanzo, na\(v\) ni kasi ya jamaa ya muafaka mbili\(S\) na\(S'\). Kasi\(v\) ni chanya kwa mwendo mbali na mwangalizi na hasi kwa mwendo kuelekea mwangalizi. Kwa upande wa mzunguko wa chanzo na mzunguko uliozingatiwa, equation hii inaweza kuandikwa kama

    \[ f_{obs} = f_s \sqrt{\frac{\left(1 - \frac{v}{c}\right)}{\left(1 + \frac{v}{c}\right)}} \label{eq20} \]

    Kumbuka kwamba ishara ni tofauti na zile za equation wavelength.

    Mfano\(\PageIndex{1}\): Calculating a Doppler Shift

    Tuseme galaksi inahamia mbali na Dunia kwa kasi 0.825 c. Inatoa mawimbi ya redio na wavelength ya

    0.525 m Ni wavelength gani tungeweza kuchunguza duniani?

    Mkakati

    Kwa sababu galaxy inahamia kwa kasi ya relativistic, tunapaswa kuamua mabadiliko ya Doppler ya mawimbi ya redio kwa kutumia mabadiliko ya Doppler ya relativistic badala ya mabadiliko ya kawaida ya Doppler.

    Suluhisho
    1. Tambua maarifa:\(u = 0.825 c\);\(\lambda_s = 0.525 \, m\).
    2. Tambua haijulikani:\(\lambda_{obs}\).
    3. Eleza jibu kama equation:

      \[\lambda_{obs} = \lambda_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}}. \nonumber \]

    4. Je! Mahesabu:

      \[\begin{align*}\lambda_{obs} &= \lambda_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}} \\[4pt] &= (0.525 \, m) \sqrt{\frac{1 + \frac{0.825c}{c}}{1 - \frac{0.825c}{c}}} \\[4pt] &= 1.70 \, m. \end{align*} \nonumber \]

    Umuhimu

    Kwa sababu galaxy inakwenda mbali na Dunia, tunatarajia wavelengths ya mionzi inayotoa kuwa nyekundu kubadilishwa. wavelength sisi mahesabu ni 1.70 m, ambayo ni nyekundu-kubadilishwa kutoka wavelength ya awali ya 0.525 m utaona katika Chembe Fizikia na Kosmolojia kwamba kuchunguza redtriffed mionzi imesababisha sasa ya siku uelewa wa asili na mageuzi ya ulimwengu.

    Zoezi\(\PageIndex{1}\)

    Tuseme probe ya nafasi inakwenda mbali na Dunia kwa kasi 0.350 c. Inatuma ujumbe wa wimbi la redio tena Duniani kwa mzunguko wa 1.50 GHz. Ujumbe uliopokea duniani ni mzunguko gani?

    Suluhisho

    Tunaweza kubadilisha data moja kwa moja kwenye equation kwa mzunguko wa Doppler wa relativistic (Equation\ ref {eq20}):

    \[\begin{align*}f_{obs} &= f_s \sqrt{\frac{1 - \frac{v}{c}}{1 + \frac{v}{c}}} \\[4pt] &= (1.50 \, GHz)\sqrt{\frac{1 - \frac{0.350c}{c}}{1 + \frac{0.350c}{c}}} \\[4pt] &= 1.04 \, GHz. \end{align*} \nonumber \]

    Athari ya Doppler ya relativistic ina maombi kuanzia ufuatiliaji wa dhoruba ya rada ya Doppler hadi kutoa taarifa juu ya mwendo na umbali wa nyota. Tunaelezea baadhi ya programu hizi katika mazoezi.