5.7: Ubadilishaji wa kasi wa Uhusiano

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Kupata equations sambamba na relativity maalum kwa ajili ya kubadilisha kasi katika sura moja inertial ya kumbukumbu katika mwingine.
• Tumia usawa wa mabadiliko ya kasi kwa vitu vinavyohamia kwa kasi ya relativistic.
• Kuchunguza jinsi kasi ya pamoja ilivyotabiriwa na equations relativistic mabadiliko kulinganisha na wale inatarajiwa classically.

Kukaa katika nafasi katika kayak katika mto haraka-kusonga inachukua juhudi. Mto wa sasa huvuta kayak pamoja. Kujaribu paddle dhidi ya mtiririko unaweza hoja Kayak mkondo jamaa na maji, lakini kwamba tu akaunti kwa ajili ya sehemu ya kasi yake jamaa na pwani. mwendo Kayak ni mfano wa jinsi kasi katika mechanics Newtonian kuchanganya na kuongeza vector. Kasi ya Kayak ni jumla ya vector ya kasi yake ikilinganishwa na maji na kasi ya maji ikilinganishwa na ukingo wa mto. Hata hivyo, kuongeza relativistic ya kasi ni tofauti kabisa.

Mabadiliko ya kasi

Fikiria gari linalosafiri usiku kando ya barabara moja kwa moja, kama ilivyo kwenye Mchoro\(\PageIndex{1}\). Dereva anaona mwanga ukiacha vichwa vya kichwa kwa kasi\(c\) ndani ya sura ya kumbukumbu ya gari. Ikiwa mabadiliko ya Galilaya yanatumika kwa mwanga, basi mwanga kutoka kwenye vichwa vya gari ungekuja kwa kasi kwa kasi\(u = v + c\), kinyume na postulates ya Einstein.

Kielelezo\(\PageIndex{1}\): Kwa mujibu wa matokeo ya majaribio na postulate ya pili ya relativity, mwanga kutoka kwa vichwa vya gari huenda mbali na gari kwa kasi\(c\) na kuelekea mwangalizi kwenye barabara ya barabara kwa kasi\(c\).

Umbali wote uliosafiri na wakati wa kusafiri ni tofauti katika muafaka wawili wa kumbukumbu, na lazima iwe tofauti kwa njia ambayo inafanya kasi ya mwanga sawa katika muafaka wote wa inertial. Sheria sahihi za kubadilisha kasi kutoka kwa sura moja hadi nyingine zinaweza kupatikana kutoka kwa usawa wa mabadiliko ya Lorentz.

Relativistic mabadiliko ya kasi

Tuseme kitu P ni kusonga kwa kasi ya mara kwa mara\(u = (u'_x, u'_y, u'_z)\) kama kipimo katika\(S'\) sura. \(S'\)Sura inahamia kando ya x'-axis kwa kasi\(v\). Katika nyongeza ya muda d', chembe ni makazi yao na\(dx'\) pamoja x'-axis. Kutumia equations ya mabadiliko ya Lorentz hutoa nyongeza zinazofanana za muda na uhamisho katika shoka zisizopangwa:

\[\begin{align} dt &= \gamma (dt' + vdx' /c^2) \\[4pt] dx &= \gamma (dx' + vdt') \\[4pt] dy &= dy' \\[4pt] dz &= dz'. \end{align} \nonumber \]

Vipengele kasi ya chembe kuonekana katika mfumo unprimed kuratibu ni basi

\[\begin{align} \dfrac{dx}{dt} &= \dfrac{\gamma(dx' + vdt')}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dx'}{dt'} + v}{1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}} \\[4pt] \dfrac{dy}{dt} &= \dfrac{dy'}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dy'}{dt'}}{\gamma \left(1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}\right)} \\[4pt] \dfrac{dz}{dt} &= \dfrac{dz'}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dz'}{dt'}}{\gamma \left(1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}\right)} \end{align} \nonumber \]

Sisi hivyo kupata equations kwa vipengele kasi ya kitu kama inavyoonekana katika sura\(S\):

\[u_x = \left(\dfrac{u'_x + v}{1 + vu'_x/c^2}\right), \, u_y = \left(\dfrac{u'_y/\gamma}{1 + vu'_x/c^2}\right), \, u_z = \left(\dfrac{u'_z/\gamma}{1 + vu'_x/c^2}\right). \nonumber \]

Linganisha hili na jinsi mabadiliko ya Galilaya ya mechanics ya classical inasema kasi inabadilika, kwa kuongeza tu kama wadudu:

\[u_x = u'_x + u, \, u_y = u'_y, \, u_z = u'_z. \nonumber \]

Wakati kasi ya jamaa ya muafaka ni ndogo sana kuliko kasi ya mwanga, yaani, wakati sheria maalum\(v\gg c,\) ya kuongeza kasi ya relativity inapunguza sheria ya kasi ya Galilaya. Wakati kasi\(v\) ya\(S'\) jamaa na\(S\) inalinganishwa na kasi ya mwanga, sheria ya kuongeza kasi ya relativistic inatoa matokeo madogo sana kuliko kuongeza kasi ya classical (Galilaya) inafanya.

Mfano\(\PageIndex{1}\): Velocity Transformation Equations for Light

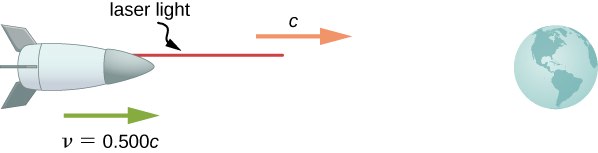
Tuseme spaceship inayoelekea moja kwa moja kuelekea Dunia kwa nusu kasi ya mwanga hutuma ishara kwetu kwenye boriti ya mwanga inayozalishwa na laser (Kielelezo\(\PageIndex{2}\)). Kutokana na kwamba mwanga huacha meli kwa kasi\(c\) kama inavyoonekana kutoka kwa meli, uhesabu kasi ambayo inakaribia Dunia.

Kielelezo\(\PageIndex{2}\): Jinsi ya kufunga gani mwanga ishara mbinu Dunia kama alimtuma kutoka spaceship kusafiri katika\(0.500c\)?

Mkakati

Kwa sababu mwanga na spaceship ni kusonga kwa kasi relativistic, hatuwezi kutumia rahisi kasi kuongeza. Badala yake, tunaamua kasi ambayo nuru inakaribia Dunia kwa kutumia kuongeza kasi ya relativistic.

Suluhisho

Tambua maarifa:\(v = 0.500c\);\(u' = c\).

Tambua haijulikani:\(u\).

Eleza jibu kama equation:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).

Je! Mahesabu:

\[ \begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + c}{1 + \dfrac{(0.500c) (c)}{c^2}} \\[4pt] &= \dfrac{(0.500 + 1)c}{\left(\dfrac{c^2 + 0.500c^2}{c^2}\right)} = c. \end{align*} \nonumber \]

Umuhimu

Relativistic kasi kuongeza inatoa matokeo sahihi. Mwanga huacha meli kwa kasi\(c\) na inakaribia Dunia kwa kasi\(c\). Kasi ya nuru ni huru na mwendo wa jamaa wa chanzo na mwangalizi, kama mwangalizi yuko kwenye meli au duniani.

Velocities haiwezi kuongeza zaidi kuliko kasi ya nuru, isipokuwa kwamba\(v\) ni chini ya\(c\) na\(u'\) hayazidi\(c\). mfano zifuatazo unaeleza kwamba relativistic kasi Aidha si kama ulinganifu kama classical kasi Aidha.

Mfano\(\PageIndex{2}\): Relativistic Package Delivery

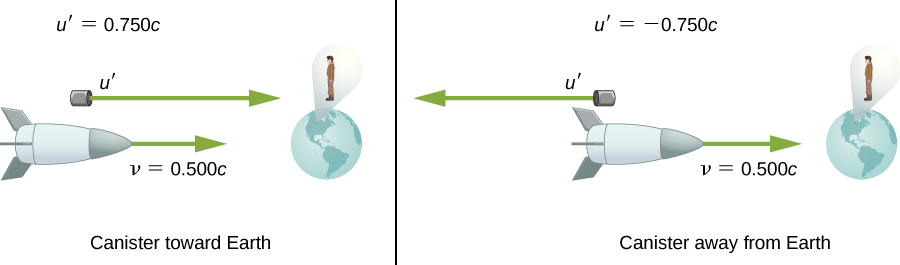
Tuseme spaceship katika mfano uliopita inakaribia Dunia kwa nusu kasi ya mwanga na shina canister kwa kasi ya\(0.750c\) (Kielelezo\(\PageIndex{3}\)).

1. Kwa kasi gani mwangalizi wa ardhi anaona canister ikiwa inapigwa risasi moja kwa moja kuelekea Dunia?
2. Kama ni risasi moja kwa moja mbali na Dunia?

Kielelezo\(\PageIndex{3}\): Canister inafukuzwa saa 0.7500c kuelekea Dunia au mbali na Dunia.

Mkakati

Kwa sababu canister na spaceship ni kusonga kwa kasi relativistic, ni lazima kuamua kasi ya canister na mwangalizi earthbound kutumia relativistic kasi Aidha badala ya kuongeza kasi rahisi.

Suluhisho kwa (a)

1. Tambua maarifa:\(v = 0.500c\);\(u' = 0.750c\).
2. Tambua haijulikani:\(u\).
3. Eleza jibu kama equation:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
4. Je! Mahesabu:\[\begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + 0.750c}{1 + \dfrac{(0.500c)(0.750c)}{c^2}} \\[4pt] &= 0.909c. \end{align*} \nonumber \]

Suluhisho kwa (b)

1. Tambua maarifa:\(v = 0.500c\);\(u' = - 0.750c\).
2. Tambua haijulikani:\(u\).
3. Eleza jibu kama equation:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
4. Je! Mahesabu:\[\begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + (-0.750c)}{1 + \dfrac{(0.500c)(-0.750c)}{c^2}} \\[4pt] &=- 0.400c. \end{align*} \nonumber \]

Umuhimu

Ishara ndogo inaonyesha kasi mbali na Dunia (kinyume chake kutoka\(v\)), ambayo inamaanisha canister inaelekea Dunia kwa sehemu (a) na mbali kwa sehemu (b), kama inavyotarajiwa. Lakini kasi za relativistic haziongeze kama vile wanavyofanya classically. Katika sehemu (a), canister inakaribia Dunia kwa kasi, lakini chini ya jumla ya vector ya kasi, ambayo ingeweza kutoa\(1.250c\). Katika sehemu (b), canister huenda mbali na Dunia kwa kasi ya -0.400c, ambayo ni kasi zaidi kuliko -0.250c inatarajiwa classically. Tofauti katika kasi sio sawa: Katika sehemu (a), mwangalizi duniani anaona canister na meli kusonga mbali kwa kasi ya 0.409 c, na kwa kasi ya 0.900 c katika sehemu (b).

Zoezi\(\PageIndex{1}\)

Umbali kando ya mwelekeo perpendicular kwa mwendo wa jamaa wa muafaka mbili ni sawa katika muafaka wote. Kwa nini basi kasi ni perpendicular kwa x -mwelekeo tofauti katika muafaka mbili?

Jibu

Ingawa uhamisho perpendicular kwa mwendo jamaa ni sawa katika muafaka wote wa kumbukumbu, muda kati ya matukio tofauti,\(dt\) na tofauti katika na\(dt'\) kusababisha kasi tofauti kuonekana kutoka muafaka mbili.