5.6: Mabadiliko ya Lorentz

Malengo ya kujifunza

• Eleza mabadiliko ya Galilaya ya mitambo ya kikabila, yanayohusiana na msimamo, wakati, kasi, na kasi zilizopimwa katika muafaka tofauti wa inertial
• Kupata sambamba Lorentz mabadiliko equations, ambayo, kinyume na mabadiliko ya Galilaya, ni sambamba na relativity maalum
• Eleza mabadiliko ya Lorentz na sifa nyingi za relativity katika suala la nne-dimensional nafasi ya wakati

Tumetumia postulates ya relativity kuchunguza, katika mifano fulani, jinsi waangalizi katika muafaka tofauti wa kumbukumbu kupima maadili tofauti kwa urefu na vipindi wakati. Tunaweza kupata ufahamu zaidi katika jinsi postulates ya relativity kubadilisha mtazamo Newton ya muda na nafasi kwa kuchunguza equations mabadiliko kwamba kutoa nafasi na wakati kuratibu ya matukio katika sura moja inertial kumbukumbu katika suala la wale katika mwingine. Sisi kwanza kuchunguza jinsi msimamo na wakati kuratibu kubadilisha kati ya muafaka inertial kulingana na mtazamo katika fizikia Newton. Kisha tunachunguza jinsi hii inapaswa kubadilishwa ili kukubaliana na postulates ya relativity. Hatimaye, sisi kuchunguza kusababisha Lorentz mabadiliko equations na baadhi ya matokeo yao katika suala la michoro nne-dimensional nafasi wakati, kusaidia mtazamo kwamba matokeo ya relativity maalum kutokana na mali ya muda na nafasi yenyewe, badala ya electromagnetism.

Milinganyo ya mabadiliko ya Galilaya

Tukio linaelezwa na mahali na wakati wake\((x, y, z, t)\) kuhusiana na sura moja ya inertial ya kumbukumbu\(S\). Kwa mfano,\((x, y, z, t)\) inaweza kuashiria msimamo wa chembe kwa wakati\(t\), na tunaweza kuangalia nafasi hizi kwa nyakati nyingi tofauti kufuata mwendo wa chembe. Tuseme sura ya pili ya kumbukumbu\(S'\) inakwenda\(v\) kwa kasi kwa heshima ya kwanza. Kwa unyenyekevu, kudhani kasi hii ya jamaa iko pamoja na x-axis. uhusiano kati ya muda na kuratibu katika muafaka mbili ya kumbukumbu ni basi

\[\begin{align} x &= x' + vt \label{eq1} \\[4pt] y &= y' \label{eq2} \\[4pt] x &= z'. \label{eq3} \end{align} \]

Thabiti katika equations hizi ni dhana kwamba vipimo vya wakati vinavyotengenezwa na waangalizi katika wote wawili\(S\) na\(S'\) ni sawa. Hiyo ni,

\[t = t' \label{eq4} \]

Equations\ ref {eq1} -\ ref {eq4} zinajulikana kwa pamoja kama mabadiliko ya Galilaya.

Tunaweza kupata kasi ya Galilaya na milinganyo ya mabadiliko ya kasi kwa kutofautisha milinganyo haya kwa heshima na wakati. Tunatumia\(u\) kwa kasi ya chembe katika sura hii ili kuitofautisha kutoka\(v\), kasi ya jamaa ya muafaka mbili za kumbukumbu. Kumbuka kwamba, kwa mabadiliko ya Galilaya, ongezeko la muda uliotumiwa katika kutofautisha kuhesabu kasi ya chembe ni sawa katika muafaka wote,\(dt = dt'\). Tofauti mavuno

\[u_x = u'_x + v, \,u_y = u'_y, \,u_z = u'_z \nonumber \]

na

\[a_x = a'_x, \,a_y = a'_y, \,a_z = a'_z. \nonumber \]

Tunaashiria kasi ya chembe na\(u\) badala ya\(v\) kuepuka kuchanganyikiwa na kasi\(v\) ya sura moja ya kumbukumbu kwa heshima na nyingine. Velocities katika kila sura hutofautiana na kasi ambayo sura moja ina kama inavyoonekana kutoka kwa sura nyingine. Waangalizi katika muafaka wote wa kumbukumbu kupima thamani sawa ya kuongeza kasi. Kwa sababu uzito haubadilishwa na mabadiliko, na umbali kati ya pointi haujafunguliwa, waangalizi katika muafaka wote wanaona vikosi sawa\(F = ma\) vinavyofanya kati ya vitu na fomu sawa ya sheria ya pili na ya tatu ya Newton katika muafaka wote wa inertial. Sheria za mechanics ni sawa na postulate ya kwanza ya relativity.

Lorentz mabadiliko equations

Mabadiliko ya Galilaya hata hivyo yanakiuka postulates ya Einstein, kwa sababu equations ya kasi inasema kwamba pigo la mwanga linalohamia kwa kasi\(c\) pamoja na x -axis ingesafiri kwa kasi\(c - v\) katika sura nyingine ya inertial. Hasa, pigo la spherical ina radius kwa\(r = ct\) wakati\(t\) katika sura isiyojulikana, na pia ina radius\(r' = ct'\) wakati t' katika sura iliyopangwa. Akielezea mahusiano haya katika kuratibu Cartesian inatoa

\[ \begin{align} x^2 + y^2 + z^2 - c^2t^2 &= 0 \label{eq21} \\[4pt] x'^2 + y'^2 + z'^2 - c^2t'^2 &= 0. \label{eq22} \end{align} \]

Pande za mkono wa kushoto Equations\ ref {eq21} na\ ref {eq22} zinaweza kuweka sawa kwa sababu zote mbili ni sifuri. Kwa sababu\(y = y'\) na\(z = z'\), sisi kupata

\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]

Hii haiwezi kuridhika kwa kasi isiyo ya sifuri ya jamaa\(v\) ya muafaka mbili ikiwa tunadhani matokeo ya mabadiliko ya Galilaya\(t = t'\) yanayotokana na\(x = x' + vt'\).

Ili kupata seti sahihi ya equations ya mabadiliko, kudhani mifumo miwili ya kuratibu\(S\) na\(S'\) katika Kielelezo\(\PageIndex{1}\). Kwanza tuseme kwamba tukio hutokea katika\(S'\) na\((x', 0, 0, t')\)\((x, 0, 0, t)\) katika\(S\), kama inavyoonyeshwa katika Kielelezo\(\PageIndex{1}\).

Kielelezo\(\PageIndex{1}\): Tukio hutokea\((x, 0, 0, t)\) katika\(S\) na\((x', 0, 0, t')\) katika\(S'\). Lorentz mabadiliko equations yanahusiana matukio katika mifumo miwili.

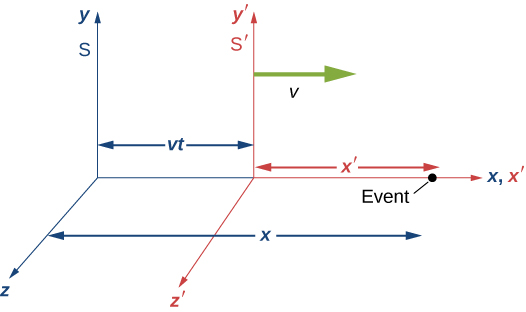
Tuseme kwamba kwa papo hapo kwamba asili ya mifumo ya kuratibu katika S na S' sanjari, bulb flash hutoa pigo spherically kueneza ya mwanga kuanzia asili. Wakati t, mwangalizi katika S anaona asili ya S' kuwa katika\(x = vt\). Kwa msaada wa rafiki katika S, mwangalizi wa S' pia hupima umbali kutoka tukio hadi asili ya S' na anaona kuwa\(x'\sqrt{1 - v^2/c^2}\). Hii ifuatavyo kwa sababu tumeonyesha tayari postulates ya relativity kuashiria contraction urefu. Hivyo nafasi ya tukio katika S ni

\[x = vt + x'\sqrt{1 - v^2/c^2} \nonumber \]

na

\[x' = \dfrac{x - vt}{x'\sqrt{1 - v^2/c^2}}. \label{eq10} \]

Postulates ya relativity inamaanisha kwamba equation inayohusiana umbali na wakati wa mbele ya wimbi la spherical:

\[x^2 + y^2 + z^2 - c^2t^2 = 0 \nonumber \]

lazima kuomba wote katika suala la kuratibu primed na unprimed, ambayo ilionyeshwa hapo juu ili kusababisha Equation:

\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]

Sisi kuchanganya hii na Equation\ ref {eq10} kwamba\(x′\) inahusiana\(x\) na kupata uhusiano kati\(t\) na\(t'\):

\[t' = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]

equations zinazohusiana wakati na nafasi ya matukio kama inavyoonekana katika\(S\) ni basi

\[ \begin{align} t &= \dfrac{t' + vx'/c^2}{\sqrt{1 - v^2/c^2}}. \\[4pt] x &= \dfrac{x' + vt'}{\sqrt{1 - v^2/c^2}}. \\[4pt] y &= y' \\[4pt] z &= z'. \end {align} \nonumber \]

Seti hii ya milinganyo, zinazohusiana na msimamo na wakati katika muafaka mbili inertial, inajulikana kama mabadiliko Lorentz. Wao ni jina kwa heshima ya H.A Lorentz (1853—1928), ambaye kwanza alipendekeza yao. Kushangaza, yeye haki mabadiliko juu ya kile hatimaye aligundua kuwa hypothesis fallacious. Msingi sahihi wa kinadharia ni nadharia maalum ya Einstein ya relativity.

Mabadiliko ya reverse yanaonyesha vigezo\(S\) katika suala la wale walio katika S'. Tu kubadilishana vigezo primed na unprimed na kubadilisha anatoa:

\[\begin{align*} t'& = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] x' &= \dfrac{x - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] y' &= y \\[4pt] z' &= z. \end{align*} \nonumber \]

Mfano\(\PageIndex{1}\): Using Lorentz Transformation for Time

Spacecraft S' iko njiani kuelekea Alpha Centauri wakati Spacecraft S inapita kwa kasi ya jamaa c /2. Nahodha wa S' anatuma ishara ya redio inayodumu 1.2 s kulingana na saa ya meli hiyo. Tumia mabadiliko ya Lorentz ili kupata muda wa ishara iliyopimwa na afisa wa mawasiliano wa spaceship S.

Suluhisho

1. Tambua inayojulikana:\(\Delta t' = t'_2 - t'_1 = 1.2 s; \,\Delta x' = x'_2 - x'_1 = 0.\)
2. Tambua haijulikani:\(\Delta t = t_2 - t_1\).
3. Eleza jibu kama equation. ishara wakati kuanza kama (\(x', t'_1\)) na ataacha katika (\(x', t'_1\)). Kumbuka kuwa kuratibu x' ya matukio yote mawili ni sawa kwa sababu saa inapumzika katika S'. Andika kwanza Lorentz mabadiliko equation katika suala la\(\Delta t = t_2 - t_1\)\(\Delta x = x_2 - x_1\),, na vile vile kwa kuratibu primed, kama:

   \[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

   Kwa sababu nafasi ya saa katika S' ni fasta,\(\Delta x' = 0\), na muda wa muda\(\Delta t\) unakuwa:

   \[\Delta t = \dfrac{\Delta t'}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

4. Kufanya hesabu.

   Na\(\Delta t' = 1.2 \,s\) hii inatoa:

   \[\begin{align*} \Delta t &= \dfrac{1.2 \,s}{\sqrt{1 - \left(\dfrac{1}{2}\right)^2}} \\[4pt] &= 1.6 \,s. \end{align*} \nonumber \]

   Kumbuka kuwa mabadiliko ya Lorentz huzalisha equation ya kupanua wakati.

Mfano\(\PageIndex{2}\): Using the Lorentz Transformation for Length

Mtafiti anapima barabara kuwa\(L = 100 \,m\) ndefu katika sura ya Dunia\(S\). Tumia mabadiliko ya Lorentz ili kupata maelezo kwa urefu wake uliopimwa kutoka kwa spaceship\(S'\), kusonga kwa kasi\(0.20c\), kuchukua\(x\) kuratibu za muafaka mbili sanjari kwa wakati\(t = 0\).

Suluhisho

1. Tambua inayojulikana:\(L = 100 \,m\);\(v = 0.20 c\);\(\Delta \tau = 0\).
2. Tambua haijulikani:\(L'\).
3. Eleza jibu kama equation. Mtafiti katika sura S amepima ncha mbili za fimbo wakati huo huo, na akawakuta wakipumzika\(x_2\) na\(x_1\) umbali\(L = x_2 - x_1 = 100 \,m\) mbali. Wafanyakazi wa spaceship hupima eneo la wakati mmoja wa mwisho wa vijiti katika sura yao. Kuhusiana urefu kumbukumbu na waangalizi katika S' na S, kwa mtiririko huo, kuandika pili ya nne Lorentz mabadiliko equations kama:

   \[\begin{align*} x'_2 - x'_1 &= \dfrac{x_2 - vt}{\sqrt{1 - v^2/c^2}} - \dfrac{x_1 - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{x_2 - x_2}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{L}{\sqrt{1 - v^2/c^2}}. \end{align*} \nonumber \]

4. Kufanya hesabu. Kwa sababu\(x_2 - x_1 = 100 \,m\), urefu wa fimbo ya kusonga ni sawa na:

   \[\begin{align*} L' &= (100 \,m)\sqrt{1 - v^2/c^2} \\[4pt] &= (100 \,m)\sqrt{1 - (0.20)^2} = 98.0 \,m. \end{align*} \nonumber \]

   Kumbuka kuwa mabadiliko Lorentz alitoa urefu contraction equation kwa mitaani.

Mfano\(\PageIndex{3}\): Lorentz Transformation and Simultaneity

Mwangalizi inavyoonekana katika Kielelezo\(\PageIndex{2}\) amesimama na nyimbo za reli anaona balbu mbili flash wakati huo huo katika ncha zote mbili za 26 m mrefu gari abiria wakati katikati ya gari hupita yake kwa kasi ya c /2. Find kujitenga katika muda kati ya wakati balbu ukaangaza kama inavyoonekana na abiria treni ameketi katikati ya gari.

Kielelezo\(\PageIndex{2}\): Mtu anayeangalia treni kwenda kwa kuona balbu mbili flash wakati huo huo katika ncha kinyume cha gari la abiria. Kuna abiria mwingine ndani ya gari akiangalia uangazavyo huo lakini kwa mtazamo tofauti.

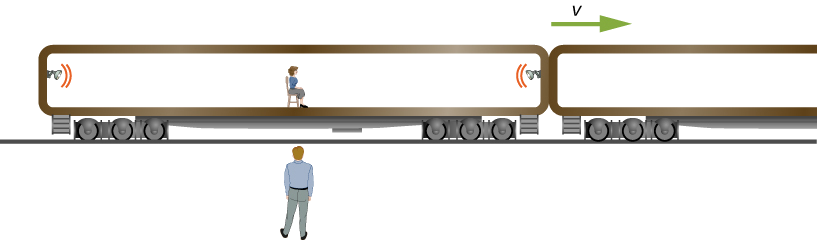
Suluhisho

1. Tambua inayojulikana:\(\Delta t = 0\).

   Kumbuka kuwa mgawanyo wa anga wa matukio mawili ni kati ya taa mbili, si umbali wa taa kwa abiria.

2. Tambua haijulikani:\(\Delta t' = t'_2 - t'_1.\).

   Tena, kumbuka kuwa muda wa muda ni kati ya taa za taa, si kati ya nyakati za kuwasili kwa kufikia abiria.

3. Eleza jibu kama equation:

   \[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]

4. Je, hesabu:

   \[\begin{align*} 0 &= \dfrac{\Delta t' + \dfrac{c}{2} (26 \,m)/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] \Delta t' &= - \dfrac{26 \,m/s}{2c} = - \dfrac{26 \,m/s}{2(3.00 \times 10^8 \,m/s)} \\[4pt] &= -4.33 \times 10^{-8}\,s. \end{align*} \nonumber \]

Umuhimu

Ishara inaonyesha kwamba tukio hilo na kubwa\(x'_2\) yaani, flash kutoka kulia, inaonekana kutokea kwanza katika sura ya S, kama ilivyopatikana mapema kwa mfano huu, ili\(t_2 < t_1\).

Nafasi Muda

Matukio ya relativistic yanaweza kuchambuliwa kwa suala la matukio katika muda wa nafasi ya nne. Wakati matukio kama vile kitendawili pacha, upanuzi wa muda, contraction ya urefu, na utegemezi wa wakati huo huo juu ya mwendo wa jamaa hutazamwa kwa njia hii, huonekana kuwa tabia ya asili ya nafasi na wakati, badala ya vipengele maalum vya electromagnetism.

Katika nafasi tatu-dimensional, nafasi zinaelezwa na kuratibu tatu kwenye seti ya axes ya Cartesian, na uhamisho wa hatua moja kutoka kwa mwingine hutolewa na:

\[(\Delta x, \,\Delta y, \,\Delta z) = (x_2 - x_1, \,y_2 - y-1, \,z_2 - z_1). \nonumber \]

Umbali\(\Delta r\) kati ya pointi ni

\[\Delta r^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2. \nonumber \]

Umbali\(\Delta r\) hauwezi kutofautiana chini ya mzunguko wa axes. Ikiwa seti mpya ya shoka za Cartesian zinazunguka karibu na asili ya jamaa na shoka za awali zinatumiwa, kila hatua katika nafasi itakuwa na kuratibu mpya kwa suala la shoka mpya, lakini umbali\(\Delta r'\) uliotolewa na

\[\Delta r'^2 = (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2. \nonumber \]

Hiyo ina thamani sawa kwamba\(\Delta r^2\) alikuwa. Kitu kama hicho kinachotokea na mabadiliko ya Lorentz katika muda wa nafasi.

Kufafanua mgawanyo kati ya matukio mawili, kila mmoja iliyotolewa na seti ya x, y, z na ct pamoja na mfumo wa nne wa Cartesian wa shoka katika muda wa nafasi, kama

\[(\Delta x, \,\Delta y, \,\Delta z, \,c\Delta t) = (x_2 - x_1, \,y_2 - y_1, \,z_2 - z_1, \,c(t_2 - t_1)). \nonumber \]

Pia kufafanua muda nafasi ya muda\(Δs\) kati ya matukio mawili kama

\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]

Kama matukio mawili na thamani sawa ya ct katika sura ya kumbukumbu kuchukuliwa,\(\Delta s\) ingekuwa yanahusiana na umbali\(\Delta r\) kati ya pointi katika nafasi.

Njia ya chembe kupitia muda wa angani ina matukio (x, y, zct) inayobainisha mahali kila wakati wa mwendo wake. Njia kupitia wakati wa nafasi inaitwa mstari wa dunia wa chembe. Mstari wa dunia wa chembe iliyobaki katika mapumziko mahali hiyohiyo ni mstari wa moja kwa moja ambao ni sambamba na mhimili wa wakati. Ikiwa chembe inakwenda kwa kasi ya mara kwa mara inayofanana na x -axis, mstari wake wa dunia ungekuwa mstari wa mteremko\(x = vt\), unaohusiana na uhamisho rahisi dhidi ya grafu ya wakati. Ikiwa chembe inaharakisha, mstari wake wa dunia umepigwa. Uongezekaji wa s kando ya mstari wa dunia wa chembe hutolewa kwa fomu tofauti kama

\[ds^2 = (dx)^2 + (dy)^2 + (dz)^2 - c^2(dt)^2. \nonumber \]

Kama vile umbali\(\Delta r\) hauwezi kutofautiana chini ya mzunguko wa shaba za nafasi, muda wa muda wa muda:

\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]

ni invariant chini ya mabadiliko Lorentz. Hii ifuatavyo kutoka postulates ya relativity, na inaweza kuonekana pia kwa badala ya uliopita Lorentz mabadiliko equations katika kujieleza kwa muda nafasi ya muda:

\[\begin{align*} \Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \\[4pt] &=\left(\dfrac{\Delta x' + v\Delta t'}{\sqrt{1 - v^2/c^2}}\right)^2 + (\Delta y')^2 + (\Delta z')^2 - \left(c\dfrac{\Delta t' + \dfrac{v\Delta x'}{c^2}}{\sqrt{1 - v^2/c^2}}\right)^2 \nonumber \]\[= (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2 - (c\Delta t')^2 \\[4pt] &= \Delta s'^2. \end{align*} \nonumber \]

Aidha, mabadiliko ya Lorentz hubadilisha kuratibu za tukio kwa wakati na nafasi sawa na jinsi mzunguko wa tatu-dimensional unabadilisha kuratibu za zamani katika kuratibu mpya:

Lorentz mabadiliko (x, t kuratibu):	Mzunguko wa mhimili kuzunguka z - mhimili (x, t kuratibu):
\(x' = (γ)x + (−βγ)ct\)	\(x' = (\cos θ)x + (\sin θ)y\)
\(ct' = (−βγ)x + (γ)ct\)	\(y' = (−\sin θ)x + (\cos θ)y\)

wapi\(\gamma = \dfrac{1}{\sqrt{1 - \beta^2}}\);\(\beta = v/c\).

Mabadiliko ya Lorentz yanaweza kuonekana kama generalizations ya mzunguko wa anga kwa muda wa nafasi. Hata hivyo, kuna baadhi ya tofauti kati ya tatu-dimensional mzunguko mhimili na Lorentz mabadiliko kuwashirikisha mhimili wakati, kwa sababu ya tofauti katika jinsi metri, au utawala kwa ajili ya kupima makazi\(\Delta r\) yao na\(\Delta s\), tofauti. Ingawa\(\Delta r\) ni invariant chini ya mzunguko anga na\(\Delta s\) ni invariant pia chini ya Lorentz mabadiliko, Lorentz mabadiliko kuwashirikisha mhimili wakati haina kuhifadhi baadhi ya vipengele, kama vile shoka iliyobaki perpendicular au urefu wadogo pamoja kila mhimili iliyobaki sawa.

Kumbuka kwamba wingi\(\Delta s^2\) unaweza kuwa na ishara ama, kulingana na kuratibu ya matukio ya nafasi wakati kushiriki. Kwa jozi ya matukio ambayo huwapa ishara hasi, ni muhimu kufafanua\(c^2 \Delta \tau^2\) kama\(-\Delta s^2\). Umuhimu wa\(c^2 \Delta \tau\) kama ilivyoelezwa tu ifuatavyo kwa kubainisha kuwa katika sura ya kumbukumbu ambapo matukio mawili hutokea katika eneo moja, tuna\(\Delta x = \Delta y = \Delta z = 0\) na kwa hiyo (kutoka equation kwa\(\Delta s^2 = - c^2 \Delta \tau^2\)):

\[c^2 \Delta \tau^2 = - \Delta s^2 = (c^2 \Delta t)^2. \nonumber \]

Kwa hiyo\(c^2 \Delta \tau\) ni muda wa muda\(c^2 \Delta t\) katika sura ya kumbukumbu ambapo matukio yote hutokea katika eneo moja. Ni muda huo wa muda mzuri kujadiliwa mapema. Pia ifuatavyo kutokana na uhusiano kati\(\Delta s\) na\(c^2 \Delta \tau\) kwamba kwa sababu\(\Delta s\) ni Lorentz invariant, wakati sahihi pia Lorentz invariant. Waangalizi wote katika muafaka wote inertial kukubaliana juu ya vipindi sahihi wakati kati ya matukio hayo mawili.

Zoezi\(\PageIndex{1}\)

Onyesha kwamba kama nyongeza wakati\(dt\) inapita kwa mwangalizi ambaye anaona chembe kusonga kwa kasi\(v\), ni sambamba na sahihi wakati chembe nyongeza kwa chembe ya\(d\tau = \gamma dt\).

Jibu

Anza na ufafanuzi wa nyongeza sahihi ya wakati:

\[d\tau = \sqrt{-(ds)^2 /c^2} = \sqrt{dt^2 - (dx^2 + dx^2 + dx^2)/c^2}. \nonumber \]

ambapo\((dx, dy, dx, cdt)\) hupimwa katika sura ya inertial ya mwangalizi ambaye si lazima kuona chembe hiyo wakati wa kupumzika. Hii kwa hiyo inakuwa

\[d\tau = \sqrt{-(ds)^2/c^2} = \sqrt{dt^2 - [(dx)^2 + (dy)^2 + (dz)^2]/c^2} \nonumber \]

\[dt\sqrt{1 - \left[ \left(\dfrac{dx}{dt}\right)^2 + \left(\dfrac{dy}{dt}\right)^2 + \left(\dfrac{dz}{dt}\right)^2\right] /c^2} \nonumber \]\[dt\sqrt{1 - v^2/c^2} \nonumber \]\[dt = \gamma d\tau. \nonumber \]

Koni ya Mwanga

Tunaweza kukabiliana na ugumu wa kutazama na kuchora michoro katika vipimo vinne kwa kufikiria viwianishi vitatu vya anga ili kuwakilishwa kwa pamoja na mhimili usio na usawa, na mhimili wima kuwa mhimili wa ct-. Kuanzia na tukio fulani katika nafasi ya wakati kama asili ya graph nafasi wakati inavyoonekana, mstari dunia ya chembe kwamba bado katika mapumziko katika eneo awali ya tukio katika asili basi ni mhimili wakati. Ndege yoyote kwa njia ya mhimili wa muda sambamba na shoka za anga ina matukio yote yanayofanana na kila mmoja na kwa makutano ya ndege na mhimili wa wakati, kama inavyoonekana katika sura nyingine ya tukio hilo katika asili.

Ni muhimu kupiga picha ya mwanga kwenye grafu, iliyoundwa na mistari ya dunia ya mihimili yote ya mwanga inayopitia tukio la asili A, kama inavyoonekana kwenye Mchoro\(\PageIndex{3}\). Koni ya mwanga, kulingana na postulates ya relativity, ina pande kwa angle ya 45° ikiwa mhimili wa muda unapimwa kwa vitengo vya ct, na, kwa mujibu wa postulates ya relativity, koni ya mwanga inabakia sawa katika muafaka wote wa inertial. Kwa sababu tukio A ni kiholela, kila hatua katika mchoro wa muda wa nafasi ina koni ya mwanga inayohusishwa nayo.

Kielelezo\(\PageIndex{3}\): Koni ya mwanga ina mistari yote ya dunia ikifuatiwa na mwanga kutoka tukio A kwenye vertex ya koni.

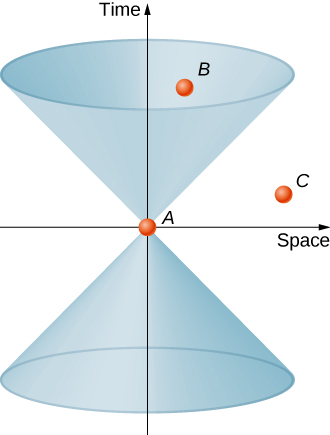
Fikiria sasa mstari wa dunia wa chembe kupitia nafasi ya wakati. Mstari wowote wa dunia nje ya koni, kama vile moja inayopita kutoka A kupitia C, itahusisha kasi kubwa kuliko c, na kwa hiyo haiwezekani. Matukio kama vile C yaliyo nje ya koni ya mwanga inasemekana kuwa na mgawanyo wa nafasi-kama na tukio A. Wao ni sifa ya:

\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - y_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]

Tukio kama B ambalo liko katika koni ya juu linaweza kupatikana bila kuzidi kasi ya mwanga katika utupu, na ina sifa

\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]

Tukio hilo linasemekana kuwa na mgawanyo wa wakati kutoka A. Matukio kama ya muda ambayo huanguka katika nusu ya juu ya koni ya mwanga hutokea kwa maadili makubwa ya t kuliko wakati wa tukio A kwenye vertex na ni katika siku zijazo jamaa na A. Matukio ambayo yanajitenga wakati kutoka A na kuanguka katika nusu ya chini ya koni ya mwanga ni katika siku za nyuma, na inaweza kuathiri tukio hilo kwa asili. Kanda nje ya koni ya mwanga huitwa kama si ya zamani wala ya baadaye, bali kama “mahali pengine.”

Kwa tukio lolote ambalo lina mgawanyo wa nafasi kutoka kwa tukio la asili, inawezekana kuchagua mhimili wa wakati ambao utafanya matukio mawili kutokea kwa wakati mmoja, ili matukio mawili yawe sawia katika sura fulani ya kumbukumbu. Kwa hiyo, ni matukio gani yenye kujitenga kwa nafasi inayokuja kabla ya nyingine kwa wakati pia inategemea sura ya kumbukumbu ya mwangalizi. Kwa kuwa kutenganishwa kwa nafasi kama kunaweza kupitishwa tu kwa kuzidi kasi ya nuru; ukiukwaji huu wa tukio ambalo linaweza kusababisha lingine hutoa hoja nyingine kwa nini chembe haziwezi kusafiri kwa kasi zaidi kuliko kasi ya mwanga, pamoja na nyenzo zinazoweza kwa sayansi ya uongo kuhusu usafiri wa muda. Vile vile kwa tukio lolote na kujitenga kwa wakati kutoka kwa tukio la asili, sura ya kumbukumbu inaweza kupatikana ambayo itafanya matukio kutokea mahali pale. Kwa sababu mahusiano

\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - x_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]

na

\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]

ni Lorentz invariant, kama matukio mawili ni wakati-kama na inaweza kufanywa kutokea katika sehemu moja au nafasi-kama na inaweza kufanywa kutokea kwa wakati mmoja ni sawa kwa waangalizi wote. Waangalizi wote katika muafaka tofauti inertial ya kumbukumbu kukubaliana na kama matukio mawili na wakati kama au nafasi kama kujitenga.

Kitendawili pacha kuonekana katika nafasi ya wakati

Kitendawili cha pacha kilichojadiliwa mapema kinahusisha pacha wa astronaut akisafiri kwa kasi ya mwanga karibu na mfumo wa nyota wa mbali, na kurudi duniani. Kwa sababu ya kupungua kwa muda, pacha ya nafasi inatabiriwa kuwa na umri mdogo kuliko pacha ya ardhi. Hii inaonekana paradoxical kwa sababu tunaweza kuwa na matarajio katika mtazamo wa kwanza kwa mwendo wa jamaa kuwa symmetrical na naively kufikiri inawezekana pia wanasema kwamba pacha earthbound lazima umri mdogo.

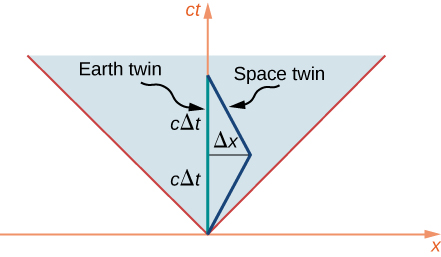
Kuchambua hili kwa suala la mchoro wa muda wa nafasi, kudhani kuwa asili ya axes kutumika ni fasta duniani. Mstari wa dunia wa pacha ya ardhi ni kisha pamoja na mhimili wa wakati.

Mstari wa dunia wa mapacha ya astronaut, ambaye husafiri kwa nyota ya mbali na kisha anarudi, lazima apotoke kwenye njia ya mstari wa moja kwa moja ili kuruhusu safari ya kurudi. Kama inavyoonekana katika Kielelezo\(\PageIndex{4}\), hali ya mapacha mawili sio sawa. Njia zao katika wakati wa nafasi ni za urefu tofauti kabisa. Hasa, mstari wa dunia ya pacha earthbound ina urefu\(2c\Delta t\), ambayo kisha anatoa muda sahihi kwamba inapita kwa pacha earthbound kama\(2\Delta t\). Umbali na mfumo wa nyota mbali ni\(\Delta x = v\Delta t\). Wakati mzuri unaopita kwa pacha ya nafasi ni\(2\Delta \tau\) wapi

\[c^2\Delta \tau^2 = - \Delta s^2 = (c\Delta t)^2 - (\Delta x)^2. \nonumber \]

Hii ni mfupi sana kuliko wakati mzuri wa mapacha ya ardhi kwa uwiano

\[\dfrac{c\Delta \tau}{c\Delta t} = \sqrt{\dfrac{(c\Delta t)^2 - (\Delta x)^2}{(c\Delta t)^2}} = \sqrt{\dfrac{(c\Delta t)^2 - (v\Delta t)^2}{(c\Delta t)^2}} = \sqrt{1 - \dfrac{v^2}{c^2}} = \dfrac{1}{\gamma}. \nonumber \]

sambamba na formula wakati dilation. Kwa hiyo, Kitendawili cha pacha kinaonekana kuwa hakuna kitendawili kabisa. Hali ya mapacha mawili haipatikani katika mchoro wa wakati wa nafasi. Mshangao pekee ni labda kwamba njia inayoonekana ya muda mrefu kwenye mchoro wa wakati wa nafasi inalingana na muda mdogo wa muda, kwa sababu ya jinsi gani\(\Delta \tau\) na\(\Delta s\) hutegemea\(\Delta x\) na\(\Delta t\).

Kielelezo\(\PageIndex{4}\). Twin nafasi na earthbound pacha, katika mfano pacha kitendawili, kufuata mistari ya dunia ya urefu tofauti kwa njia ya nafasi ya muda.

Lorentz Mabadiliko katika Nafasi wakati

Tumebainisha jinsi mabadiliko ya Lorentz yanavyoacha

\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]

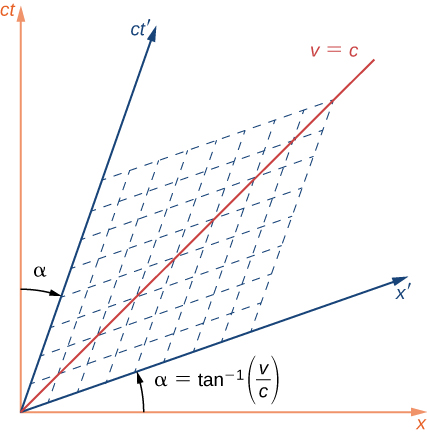
bila kubadilika na inafanana na mzunguko wa axes katika muda wa nafasi ya nne. Kama S na S' muafaka ni katika mwendo jamaa pamoja x -direction yao pamoja nafasi na wakati shoka ya S' ni kuzungushwa na angle αα kama inavyoonekana kutoka S, kwa njia inavyoonekana katika Kielelezo\(\PageIndex{5}\), ambapo:

\[tan \,\alpha = \dfrac{v}{c} = \beta. \nonumber \]

Hii inatofautiana na mzunguko kwa maana ya kawaida ya mwelekeo wa tatu, kama vile shoka mbili za muda zinazunguka kwa kila mmoja kwa njia ya mkasi, kama inavyoonekana. Mzunguko wa muda na nafasi za nafasi ni wote kwa njia ya pembe sawa. Mesh ya mistari iliyopigwa sambamba na axes mbili zinaonyesha jinsi kuratibu za tukio zingesomwa pamoja na axes zilizopangwa. Hii itakuwa kufanyika kwa kufuata mstari sambamba na x 'na moja sambamba na t'-mhimili, kama inavyoonekana kwa mistari dashed. Kiwango cha urefu wa axes zote mbili kinabadilishwa na:

\[ct' = ct\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}; \,x' = x\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}. \nonumber \]

Mstari ulioitwa “v = c” saa 45° hadi x -axis inalingana na makali ya koni ya mwanga, na hauathiriwa na mabadiliko ya Lorentz, kwa mujibu wa postulate ya pili ya relativity. Mstari wa “v = c”, na koni ya mwanga inawakilisha, ni sawa kwa sura ya S na S' ya kumbukumbu.

Kielelezo\(\PageIndex{5}\): Matokeo ya mabadiliko ya Lorentz katika nafasi mpya na shaba za wakati zinazungushwa kwa njia ya mkasi kwa heshima na shaba za awali.

Wakati huo huo

Sambamba ya matukio katika maeneo yaliyotengwa inategemea sura ya kumbukumbu inayotumiwa kuelezea, kama ilivyotolewa na “mzunguko” wa mkasi kwa kuratibu mpya na nafasi kama ilivyoelezwa. Kama matukio mawili na\(t\) maadili sawa katika sura unprimed ya kumbukumbu, hawana haja ya kuwa na maadili sawa kipimo pamoja\(ct'\) -axis, na bila kuwa samtidiga katika sura primed.

Kama mfano maalum, fikiria treni ya karibu-mwanga-kasi ambayo taa za flash kwenye ncha mbili za gari zimeangaza wakati huo huo katika sura ya kumbukumbu ya mwangalizi chini. Grafu ya muda wa nafasi inavyoonyeshwa Kielelezo\(\PageIndex{6}\). Mwangaza wa taa hizo mbili zinawakilishwa na dots zilizoitwa “Taa ya kushoto ya kushoto” na “taa ya kulia ya taa” ambayo iko kwenye koni ya mwanga katika siku za nyuma. Mstari wa dunia wa kunde zote mbili husafiri kando ya koni ya mwanga ili kufika kwa mwangalizi ardhini wakati huo huo. Kuwasili kwao ni tukio la asili. Kwa hiyo ilibidi kutolewa wakati huo huo katika sura unprimed, kama inawakilishwa na hatua kinachoitwa kama\(t\) (wote). Lakini wakati hupimwa kando ya mhimili wa ct katika sura ya kumbukumbu ya mwangalizi ameketi katikati ya gari la treni. Hivyo katika sura yake ya kumbukumbu, tukio la chafu la balbu lililoandikwa kama\(t'\) (kushoto) na\(t'\) (kulia) halikuwa wakati huo huo.

Kielelezo\(\PageIndex{6}\): mfano treni upya. Uangazavyo hutokea kwa wakati mmoja t (wote) pamoja na mhimili wa wakati wa mwangalizi wa ardhi, lakini kwa nyakati tofauti, pamoja na mhimili wa wakati wa abiria.

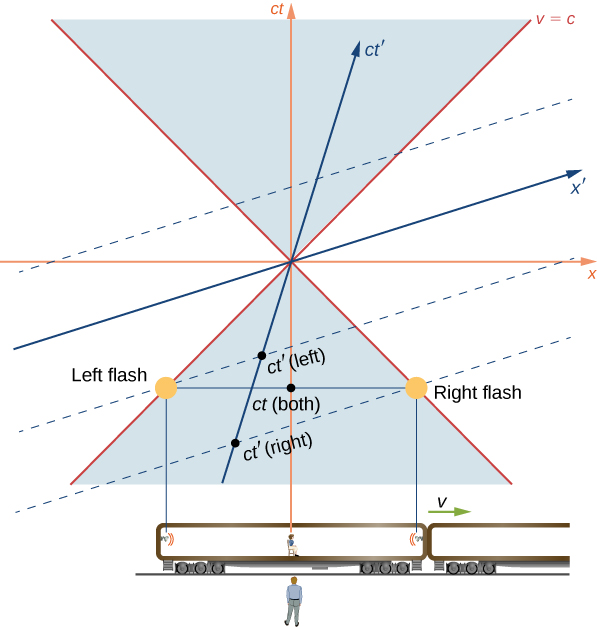
Kwa upande wa mchoro wa muda wa nafasi, waangalizi wawili wanatumia tu shaba tofauti za wakati kwa matukio sawa kwa sababu wao ni katika muafaka tofauti wa inertial, na hitimisho la waangalizi wote ni sawa halali. Kama uchambuzi katika suala la michoro ya muda wa nafasi unaonyesha zaidi, mali ya jinsi wakati huo huo wa matukio inategemea sura ya matokeo ya kumbukumbu kutoka kwa mali ya nafasi na wakati yenyewe, badala ya kitu chochote hasa kuhusu electromagnetism.