5.5: Urefu wa Urefu

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza jinsi wakati huo huo na urefu wa contraction ni kuhusiana.
• Eleza uhusiano kati ya contraction urefu na muda dilation na matumizi yake kwa kupata urefu-contraction equation.

Urefu wa gari la treni katika Kielelezo\(\PageIndex{1}\) ni sawa kwa abiria wote. Wote wangekubaliana juu ya eneo la wakati mmoja wa mwisho wa gari na kupata matokeo sawa kwa umbali kati yao. Lakini matukio ya wakati mmoja katika sura moja ya inertial haipaswi kuwa wakati huo huo katika mwingine. Ikiwa treni ingeweza kusafiri kwa kasi ya relativistic, mwangalizi ardhini angeona maeneo ya wakati mmoja wa mwisho wa gari kwa umbali tofauti mbali na waangalizi ndani ya gari. Umbali wa kipimo hauhitaji kuwa sawa kwa waangalizi tofauti wakati kasi ya relativistic inahusika.

Kielelezo\(\PageIndex{1}\): Watu wanaweza kuelezea umbali tofauti, lakini kwa kasi ya relativistic, umbali kweli ni tofauti. (mikopo: “russavia” /Flickr).

Urefu sahihi

Waangalizi wawili wanaopita kila mmoja daima wanaona thamani sawa ya kasi yao ya jamaa. Ingawa muda dilation ina maana kwamba treni abiria na mwangalizi amesimama pamoja tracks kupima nyakati tofauti kwa treni kupita, bado wanakubaliana kwamba kasi jamaa, ambayo ni umbali kugawanywa na muda uliopita, ni sawa. Ikiwa mwangalizi ardhini na mmoja kwenye treni hupima muda tofauti kwa urefu wa treni kupita mwangalizi wa ardhi, kukubaliana juu ya kasi yao ya jamaa inamaanisha lazima pia kuona umbali tofauti uliosafiri.

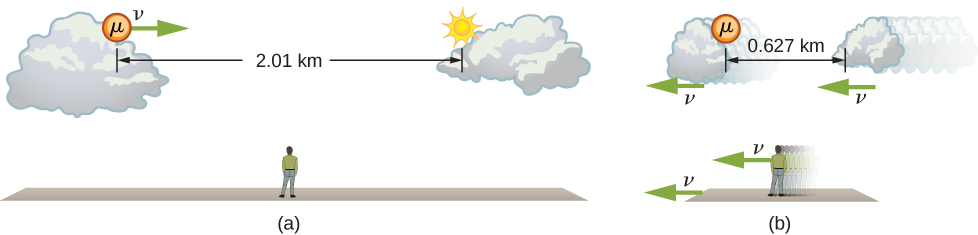
Muon kujadiliwa hapo awali inaonyesha dhana hii (Kielelezo\(\PageIndex{2}\)). Kwa mwangalizi duniani, muoni husafiri saa 0.950 c kwa 7.05 μs kutoka wakati unapozalishwa hadi kuoza. Kwa hiyo, husafiri umbali jamaa na Dunia ya:

\[ \begin{align*} L_0 &= v\Delta t \\[4pt] &= (0.950)(3.00 \times 10^8 \, m/s)(7.05 \times 10^{-6}s) \\[4pt] &= 2.01 \, km. \end{align*} \nonumber \]

Katika sura ya muon, maisha ya muon ni 2.20 μs. Katika sura hii ya kumbukumbu, Dunia, hewa, na ardhi zina muda wa kutosha wa kusafiri:

\[ \begin{align*} L &= v\Delta r \\[4pt] &= (0.950)(3.00 \times 10^8 \, m/s)(2.20 \times 10^{-6}s) \\[4pt] &= 0.627 \, km. \end{align*} \nonumber \]

Umbali kati ya matukio mawili yale (uzalishaji na kuoza kwa muon) inategemea nani anayeipima na jinsi wanavyohamia jamaa nayo.

Ufafanuzi: Urefu sahihi

Urefu sahihi\(L_0\) ni umbali kati ya pointi mbili zilizopimwa na mwangalizi ambaye anapumzika kuhusiana na pointi zote mbili.

Mwangalizi wa ardhi hupima urefu sahihi\(L_0\) kwa sababu pointi ambazo muon huzalishwa na kuoza ni stationary jamaa na Dunia. Kwa muoni, Dunia, hewa, na mawingu huhamia, hivyo umbali L unaoona sio urefu sahihi.

Kielelezo\(\PageIndex{2}\): (a) Mwangalizi wa ardhi anaona usafiri wa muon 2.01 km. (b) Njia hiyo ina urefu wa kilomita 0.627 inayoonekana kutoka sura ya kumbukumbu ya muon. Dunia, hewa, na mawingu huhamia jamaa na muoni katika sura yake, na kuwa na urefu mdogo kando ya usafiri.

Urefu Contraction

Ili kuhusisha umbali uliopimwa na waangalizi tofauti, kumbuka kuwa kasi inayohusiana na mwangalizi wa ardhi katika mfano wetu wa muon hutolewa na

\[v = \dfrac{L_0}{\Delta t}. \nonumber \]

Wakati unaohusiana na mwangalizi wa ardhi ni\(Δt\), kwa sababu kitu kinachopangwa wakati ni kusonga jamaa na mwangalizi huyu. Jamaa ya kasi na mwangalizi wa kusonga hutolewa na

\[v = \dfrac{L}{\Delta \tau}. \nonumber \]

Mwangalizi wa kusonga husafiri na muon na kwa hiyo anaona wakati unaofaa\(\Delta \tau\). Velocities mbili ni sawa; hivyo,

\[\dfrac{L_0}{\Delta t} = \dfrac{L}{\Delta \tau}. \label{eq10} \]

Tunajua kwamba\(\Delta t = \gamma \Delta \tau\) na kubadilisha hii katika Equation\ ref {eq10} anatoa

\[L = \dfrac{L_0}{\gamma}. \nonumber \]

Kubadilisha kwa\(γ\) inatoa equation zinazohusiana umbali kipimo na waangalizi tofauti.

Ufafanuzi: Upungufu wa urefu

Upungufu wa urefu ni kupungua kwa urefu uliopimwa wa kitu kutoka urefu wake sahihi wakati unapopimwa katika sura ya kumbukumbu inayohamia kwa heshima na kitu:

\[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} \label{contraction} \]

\(L_0\)wapi urefu wa kitu katika sura yake ya kupumzika, na\(L\) ni urefu katika sura inayohamia kwa kasi\(v\).

Kama sisi kupima urefu wa kitu chochote kusonga jamaa na sura yetu, sisi kupata urefu wake L kuwa ndogo kuliko urefu sahihi\(L_0\) ambayo itakuwa kipimo kama kitu walikuwa stationary. Kwa mfano, katika sura ya kupumzika ya muoni, umbali wa Dunia unahamia kati ya mahali ambapo muoni ulizalishwa na mahali ulipoooharibika ni mfupi kuliko umbali uliosafiri kama unavyoonekana kutoka kwenye sura ya Dunia. Pointi hizo ni fasta jamaa na Dunia lakini zinahamia jamaa na muoni. Mawingu na vitu vingine pia huambukizwa pamoja na mwelekeo wa mwendo kama inavyoonekana kutoka sura ya kupumzika ya muon.

Kwa hiyo, waangalizi wawili hupima umbali tofauti pamoja na mwelekeo wao wa mwendo wa jamaa, kulingana na nani anayepima umbali kati ya vitu vinavyopumzika.

Lakini vipi kuhusu umbali uliopimwa katika mwelekeo perpendicular kwa mwendo wa jamaa? Fikiria waangalizi wawili kusonga pamoja x yao -axes na kupita kila mmoja wakati kufanya mita vijiti wima katika y -direction. Kielelezo\(\PageIndex{3}\) kinaonyesha vijiti vya mita mbili M na M' ambavyo vinapumzika katika muafaka wa kumbukumbu ya wavulana wawili S na S', kwa mtiririko huo. Paintbrush ndogo ni masharti ya juu (alama 100-cm) ya fimbo M'. Tuseme kwamba S' ni kuhamia haki kwa kasi sana v jamaa na S, na vijiti ni oriented ili waweze perpendicular, au transverse, kwa vector yao jamaa kasi. Vijiti vinafanyika ili waweze kupitiana, mwisho wao wa chini (alama ya 0-cm) sanjari. Kudhani kwamba wakati S inaangalia fimbo yake M baadaye, yeye anaona line walijenga juu yake, tu chini ya juu ya fimbo. Kwa sababu brashi ni masharti ya juu ya fimbo mvulana mwingine M', S inaweza tu kuhitimisha kwamba fimbo M' ni chini ya 1.0 m mrefu.

Kielelezo\(\PageIndex{3}\): Mita vijiti M na M'M ni stationary katika muafaka kumbukumbu ya waangalizi S na S, kwa mtiririko huo. Kama vijiti vinavyopita, brashi ndogo iliyounganishwa na alama ya 100-cm ya M' huweka mstari kwenye M.

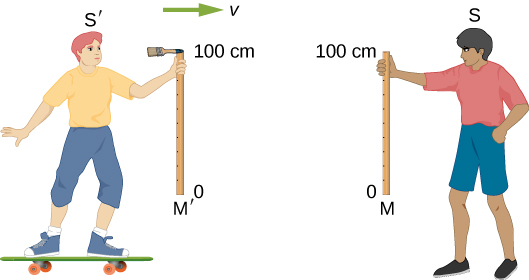
Sasa wakati wavulana mbinu kila mmoja, ', kama S, anaona mita fimbo kusonga mbele yake kwa kasi v. Kwa sababu hali zao ni sawa, kila mvulana lazima afanye kipimo sawa cha fimbo katika sura nyingine. Hivyo, kama S hatua fimbo M' kuwa chini ya 1.0 m mrefu, 'lazima kupima fimbo M kuwa pia chini ya 1.0 m mrefu, na' lazima kuona paintbrush yake kupita juu ya juu ya fimbo M na si rangi line juu yake. Kwa maneno mengine, baada ya tukio hilo, mvulana mmoja anaona mstari uliojenga kwenye fimbo, wakati mwingine haoni mstari huo kwenye fimbo hiyo!

Einstein ya kwanza postulate inahitaji kwamba sheria za fizikia (kama, kwa mfano, kutumika kwa uchoraji) kutabiri kwamba S na S, ambao ni katika muafaka inertial, kufanya uchunguzi huo; yaani, S na S' lazima aidha wote kuona mstari walijenga juu ya fimbo M, au wote hawaoni mstari huo. Kwa hiyo sisi ni kulazimishwa kuhitimisha dhana yetu ya awali kwamba S aliona line walijenga chini ya juu ya fimbo yake ilikuwa na makosa! Badala yake, S hupata mstari uliojenga haki kwenye alama ya cm 100 kwenye M. kisha wavulana wote watakubaliana kwamba mstari umejenga kwenye M, nao pia watakubaliana kwamba vijiti vyote ni sawa na m 1. Tunahitimisha basi kwamba vipimo vya urefu wa transverse lazima iwe sawa katika muafaka tofauti wa inertial.

Mfano\(\PageIndex{4}\): Calculating Length Contraction

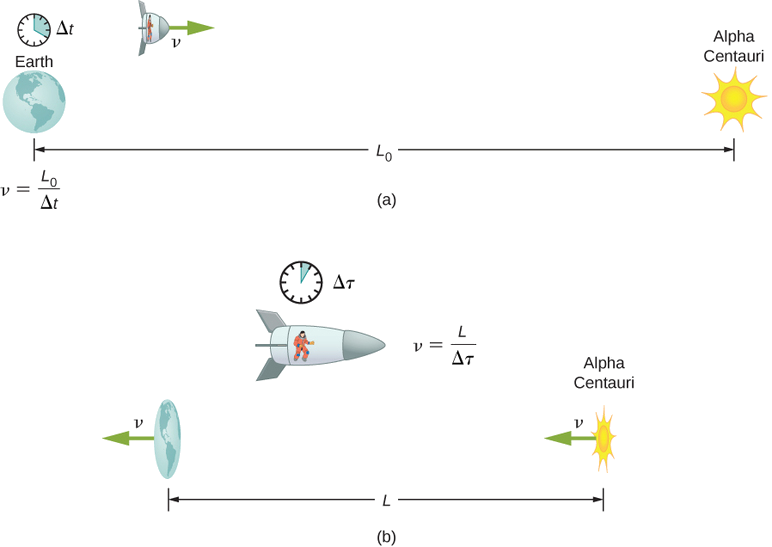
Tuseme astronaut, kama vile pacha katika majadiliano pacha kitendawili, husafiri kwa kasi kwamba\(\gamma = 30.00\). (a) Mwanaanga husafiri kutoka Dunia kwenda kwenye mfumo wa nyota wa karibu, Alpha Centauri, umbali wa miaka ya nuru 4.300 (ly) kama kipimo cha mwangalizi wa dunia. Jinsi mbali mbali Dunia na Alpha Centauri kama kipimo na astronaut? (b) Kwa upande wa c, kasi ya mwanaanga ni jamaa gani na Dunia? Unaweza kupuuza mwendo wa Dunia kuhusiana na jua (Kielelezo\(\PageIndex{4}\)).

Kielelezo\(\PageIndex{4}\): (a) Mwangalizi wa ardhi hupima umbali sahihi kati ya Dunia na Alpha Centauri. (b) Mwanaanga anaona contraction urefu kwa sababu Dunia na Alpha Centauri hoja jamaa na meli yake. Anaweza kusafiri umbali huu mfupi kwa muda mdogo (wakati wake sahihi) bila kuzidi kasi ya mwanga.

Mkakati

Kwanza, kumbuka kuwa mwaka wa nuru (ly) ni kitengo rahisi cha umbali kwenye kiwango cha astronomia—ni umbali wa mwanga unaosafiri kwa mwaka. Kwa sehemu (a) umbali wa 4.300-ly kati ya Alpha Centauri na Dunia ni umbali sahihi\(L_0\), kwa sababu hupimwa na mwangalizi wa dunia ambaye nyota zote mbili zina (takriban) stationary. Kwa astronaut, Dunia na Alpha Centauri huhamia nyuma kwa kasi sawa, hivyo umbali kati yao ni urefu ulioambukizwa L. Katika sehemu (b), tunapewa\(\gamma\), ili tuweze kupata\(v\) kwa upya upya ufafanuzi wa\(\gamma\) kuelezea\(v\) kwa suala la\(c\).

Suluhisho kwa (a)

Kwa sehemu (a):

1. Tambua maarifa:\(L_0 = 4.300 \, ly\);\(\gamma = 30.00.\)
2. Tambua haijulikani: L.
3. Eleza jibu kama equation:\(L = \dfrac{L_0}{\gamma}\).
4. Je! Mahesabu:

   \[\begin{align*} L &= \dfrac{L_0}{\gamma} \\[4pt] &= \dfrac{4.300 \, ly}{30.00} \\[4pt] &= 0.1433 \, ly. \end{align*} \nonumber \]

Suluhisho kwa (b)

Kwa sehemu (b):

1. Tambua inayojulikana:\(\gamma = 30.00\).
2. Kutambua haijulikani: v katika suala la c.
3. Eleza jibu kama equation. Anza na:

   \[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

   Kisha kutatua kwa v/c haijulikani kwa kwanza kupiga pande zote mbili na kisha upya upya:

   \[\begin{align*} \gamma^2 &= \dfrac{1}{1 - \dfrac{v^2}{c^2}} \\[4pt] \dfrac{v^2}{c^2} &= 1 - \dfrac{1}{\gamma^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - \dfrac{1}{\gamma^2}}. \end{align*} \nonumber \]

4. Je! Mahesabu:

   \[\begin{align*} \dfrac{v}{c} &= \sqrt{1 - \dfrac{1}{\gamma^2}} \\[4pt] &= \sqrt{1 - \dfrac{1}{(30.00)^2}} \\[4pt] &= 0.99944\end{align*} \nonumber \]

   au

   \[v = 0.9994 \, c. \nonumber \]

Umuhimu: Kumbuka si kuzunguka mahesabu mpaka jibu la mwisho, au unaweza kupata matokeo mabaya. Hii ni kweli hasa kwa mahesabu maalum ya relativity, ambapo tofauti zinaweza kufunuliwa tu baada ya maeneo kadhaa ya decimal. Athari ya relativistic ni kubwa hapa (\(\gamma = 30.00\)), na tunaona kwamba v inakaribia (si sawa) kasi ya mwanga. Kwa sababu umbali kama kipimo na astronaut ni mdogo sana, astronaut anaweza kusafiri kwa muda mdogo sana katika sura yake.

Watu wanaosafiri kwa kasi ya juu sana wanaweza kufikia umbali mkubwa sana (maelfu au hata mamilioni ya miaka ya mwanga) na umri wa miaka michache tu njiani. Hata hivyo, kama wahamiaji katika karne zilizopita walioacha nyumbani kwao, watu hawa wangeondoka duniani wanayoijua milele. Hata kama walirudi, maelfu hadi mamilioni ya miaka ingekuwa yamepita duniani, kuharibu zaidi ya yale yaliyopo sasa. Pia kuna kikwazo kikubwa zaidi cha kusafiri kwa kasi kama hiyo; nguvu kubwa zaidi zitahitajika ili kufikia kasi ya juu kama ya fizikia ya kawaida kuliko fizikia ya kawaida inabiri inaweza kupatikana. Hii itajadiliwa baadaye katika sura.

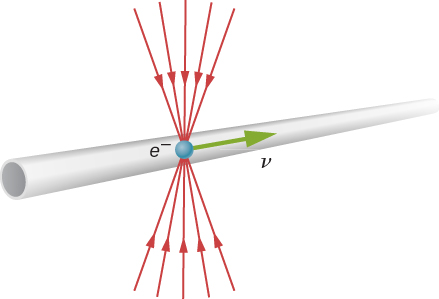
Kwa nini hatujui contraction urefu katika maisha ya kila siku? Umbali wa duka la vyakula hauonekani kutegemea kama tunahamia au la. Kuchunguza Equation\ ref {contraction}, tunaona kwamba katika kasi ya chini (\(v \ll c\)), urefu ni karibu sawa, ambayo ni matarajio classical. Hata hivyo, contraction urefu ni halisi, kama si kawaida uzoefu. Kwa mfano, chembe ya kushtakiwa kama vile elektroni inayosafiri kwa kasi ya relativistic ina mistari ya uwanja wa umeme ambayo imesisitizwa pamoja na mwelekeo wa mwendo kama inavyoonekana na mwangalizi wa stationary (Kielelezo\(\PageIndex{5}\)). Kama elektroni inapita detector, kama vile coil ya waya, uwanja wake huingiliana kwa ufupi zaidi, athari aliona katika accelerators chembe kama vile 3-km-mrefu Stanford Linear Accelerator (SLAC). Kwa kweli, kwa elektroni inayosafiri chini ya bomba la boriti kwenye SLAC, kasi ya kasi na Dunia yote huhamia na ni urefu ulioambukizwa. Athari ya relativistic ni kubwa sana kwamba kasi ni 0.5 m tu kwa muda mrefu kwa elektroni. Kwa kweli ni rahisi kupata boriti ya elektroni chini ya bomba, kwa sababu boriti haipaswi kuwa sawa na lengo la kushuka bomba fupi kama ingekuwa chini ya bomba 3 km kwa muda mrefu. Hii, tena, ni uthibitisho wa majaribio ya nadharia maalum ya relativity.

Kielelezo\(\PageIndex{5}\): Mstari wa uwanja wa umeme wa chembe ya juu ya kasi ya kushtakiwa imesisitizwa kando ya mwelekeo wa mwendo na contraction ya urefu, huzalisha ishara tofauti inayoonekana kama chembe inapita kupitia coil.

Zoezi\(\PageIndex{1}\)

Chembe inasafiri kupitia angahewa ya Dunia kwa kasi ya\(0.750c\). Kwa mtazamaji wa ardhi, umbali unaotembea ni kilomita 2.50. Jinsi mbali chembe kusafiri kama kutazamwa kutoka sura ya kumbukumbu ya chembe?

Jibu

\[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} = (2.50 \, km)\sqrt{1 - \dfrac{(0.750c)^2}{c^2}} = 1.65 \, km \nonumber \]