5.4: Kupanua kwa muda

Last updated
Save as PDF

Page ID: 175421

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Eleza jinsi vipindi vya muda vinaweza kupimwa tofauti katika muafaka tofauti wa kumbukumbu.
Eleza jinsi ya kutofautisha muda sahihi wa muda kutoka kwa muda wa muda uliopanuliwa.
Eleza umuhimu wa majaribio ya muon.
Eleza kwa nini kitendawili cha mapacha sio tofauti.
Tumia muda wa kupanua kutokana na kasi ya kitu katika sura iliyotolewa.

Uchunguzi wa wakati huo huo unaonyesha kwamba postulates ya Einstein inamaanisha athari muhimu: Vipindi vya muda vina maadili tofauti wakati unapimwa katika muafaka tofauti wa inertial. Tuseme, kwa mfano, astronaut hatua wakati inachukua kwa mapigo ya mwanga kusafiri umbali perpendicular mwelekeo wa mwendo wa meli yake (jamaa na mwangalizi earthbound), bounce mbali kioo, na kurudi (Kielelezo\(\PageIndex{1a}\)). Je, wakati uliopita ambao astronaut hatua katika spacecraft kulinganisha na muda uliopita kwamba mwangalizi earthbound hatua kwa kuchunguza kinachotokea katika spacecraft?

Kuchunguza swali hili husababisha matokeo makubwa. Wakati uliopita wa mchakato unategemea ni mwangalizi anayeipima. Katika kesi hiyo, muda uliopimwa na astronaut (ndani ya spaceship ambapo astronaut anapumzika) ni ndogo kuliko wakati uliopimwa na mtazamaji wa ardhi (ambaye astronaut anahamia). Wakati uliopita kwa ajili ya mchakato huo ni tofauti kwa waangalizi, kwa sababu umbali mwanga mapigo husafiri katika sura astronaut ni ndogo kuliko katika sura earthbound, kama inavyoonekana katika Kielelezo\(\PageIndex{1b}\). Mwanga husafiri kwa kasi sawa katika kila sura, hivyo inachukua muda zaidi kusafiri umbali mkubwa katika sura ya ardhi.

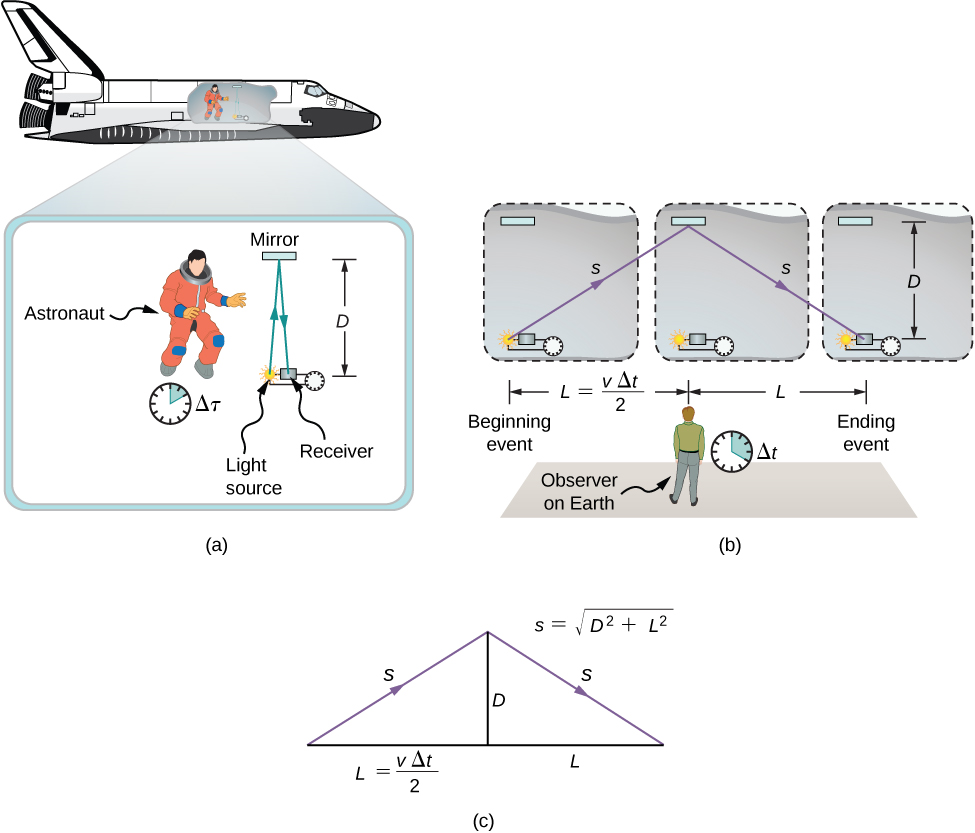
Kielelezo a inaonyesha mfano wa mwanaanga katika kuhamisha nafasi kuchunguza saa Analog na muda uliopita Delta tau. Maelezo ya jaribio la saa pia yanaonyeshwa kama ifuatavyo: Kuna chanzo cha mwanga, mpokeaji umbali mfupi na haki yake, na kioo kilichozingatia juu yao. umbali wima kutoka receiver na chanzo mwanga kwa kioo kinachoitwa kama D. njia ya mwanga kutoka chanzo, hadi kioo, na nyuma chini ya receiver inavyoonekana. Kielelezo b inaonyesha mwangalizi duniani na saa Analog kuonyesha muda wa muda Delta t Juu ya waangalizi ni michoro tatu kuonyesha majaribio saa juu ya kuhamisha nafasi katika nyakati tatu tofauti na njia ya mwanga. Chanzo cha mwanga katika mchoro upande wa kushoto kinachoitwa “tukio la mwanzo.” Mpokeaji katika mchoro upande wa kulia anaitwa “tukio la mwisho.” Njia ya mwanga hufanya mstari wa moja kwa moja kwenda diagonally juu na kulia, kutoka chanzo katika mchoro upande wa kushoto kwa kioo katika mchoro katikati, na kisha mstari mwingine wa moja kwa moja kwenda diagonally chini na kulia, kutoka kioo katikati mchoro kwa mpokeaji katika mchoro upande wa kulia . umbali wima kutoka mpokeaji kwa kioo kinachoitwa D. umbali usawa kutoka tukio mwanzo kwa saa eneo katika kituo cha mchoro kinachoitwa L= v Delta t juu 2. Umbali usio na usawa kutoka eneo la saa katika mchoro wa kituo hadi tukio la mwisho linaitwa L. Mchoro c inaonyesha pembetatu ya isosceles na msingi usio na usawa. Pembetatu imegawanywa na mstari wa wima kutoka kilele chake hadi msingi wake ndani ya pembetatu mbili zinazofanana na mstari wa wima unaojenga upande unaoshirikiwa na pembetatu mbili za kulia. Upande huu ni kinachoitwa D. msingi wa pembetatu upande wa kushoto ni kinachoitwa L = v Delta t juu 2. Msingi wa pembetatu upande wa kulia ni kinachoitwa L. hypotenuse ya kila pembetatu sahihi ni kinachoitwa s Juu mchoro ni equation s sawa na mizizi ya mraba ya wingi D squared pamoja L squared. — Kielelezo\(\PageIndex{1}\): (a) astronaut hatua muda\(\Delta \tau\) kwa ajili ya mwanga kusafiri umbali 2D katika sura astronaut ya. (b) Mwanasayansi wa NASA duniani anaona nuru kufuata njia ndefu 2s na kuchukua muda mrefu zaidi\(\Delta t\). (c) Pembetatu hizi hutumiwa kupata uhusiano kati ya umbali mbili D na s.

Ufafanuzi: Muda wa Kupanua

Muda dilation - Lengthening muda kati ya matukio mawili kwa waangalizi katika sura inertial, ambayo ni kusonga kwa heshima na wengine sura ya matukio (ambapo matukio kutokea katika eneo moja).

Kwa quantitatively kulinganisha vipimo wakati katika muafaka mbili inertial, tunaweza kuhusisha umbali katika Kielelezo\(\PageIndex{1b}\) kwa kila mmoja, kisha kueleza kila umbali katika suala la muda wa kusafiri (mtiririko aidha\(\Delta t\) au\(\Delta \tau\)) ya mapigo katika sura sambamba kumbukumbu. equation kusababisha inaweza kisha kutatuliwa kwa\(\Delta t\) katika suala la\(\Delta \tau\).

Urefu\(D\) na\(L\) katika Kielelezo\(\PageIndex{1c}\) ni pande za pembetatu sahihi na hypotenuse\(s\). Kutoka theorem ya Pythagorean,

\[s^2 = D^2 + L^2. \nonumber \]

Urefu\(2s\) na\(2L\) ni, kwa mtiririko huo, umbali ambao pigo la mwanga na spacecraft husafiri kwa wakati\(\Delta t\) katika sura ya waangalizi wa ardhi. Urefu\(D\) ni umbali ambao pigo la mwanga husafiri kwa wakati\(\Delta \tau\) katika sura ya astronaut. Hii inatupa milinganyo mitatu:

\[\begin{align*} 2s &= c\Delta t \\[4pt] 2L &= v\Delta t; \\[4pt] 2D &= c\Delta \tau. \end{align*} \nonumber \]

Kumbuka kwamba tulitumia postulate ya pili ya Einstein kwa kuchukua kasi ya mwanga kuwa c katika muafaka wote inertial. Tunachukua matokeo haya katika maneno ya awali kutoka kwa theorem ya Pythagorean:

\[ \begin{align*} s^2 &= D^2 + L^2 \\[4pt] \left(c\dfrac{\Delta t}{2}\right)^2 &= \left(c\dfrac{\Delta \tau}{2}\right)^2 + \left(v\dfrac{\Delta t}{2}\right)^2 \end{align*} \nonumber \]

Kisha sisi upya ili kupata

\[(c\Delta t)^2 - (v\Delta t)^2 = (c\Delta \tau)^2. \nonumber \]

Hatimaye, kutatua kwa\(\Delta t\) katika suala la\(\Delta \tau\) inatupa

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - (v/c)^2}}. \nonumber \]

Hii ni sawa na

\[\Delta t = \gamma \Delta \tau, \label{timedilation} \]

ambapo\(\gamma\) ni sababu relativistic (mara nyingi huitwa sababu Lorentz) iliyotolewa na

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} \nonumber \]

\(v\)na\(c\) ni kasi ya mwangalizi kusonga na mwanga, kwa mtiririko huo.

Angalia asymmetry kati ya vipimo viwili. Moja tu kati yao ni kipimo cha muda kati ya matukio mawili-chafu na kuwasili kwa pigo la mwanga-katika nafasi sawa. Ni kipimo cha muda wa muda katika sura iliyobaki ya saa moja. Kipimo katika sura ya ardhi kinahusisha kulinganisha muda wa muda kati ya matukio mawili yanayotokea katika maeneo tofauti. Muda wa muda kati ya matukio yanayotokea mahali pekee una jina tofauti ili kuitofautisha na wakati uliopimwa na mwangalizi wa ardhi, na tunatumia alama tofauti\(\Delta \tau\) ili kuitaja katika sura hii.

Ufafanuzi: Muda sahihi

Muda sahihi wa muda\(\Delta \tau\) kati ya matukio mawili ni kipindi cha muda kilichopimwa na mwangalizi ambaye matukio yote hutokea katika eneo moja.

equation zinazohusiana\(\delta t\) na\(\Delta \tau\) ni kweli ajabu. Kwanza, kama ilivyoelezwa hapo awali, muda uliopita si sawa kwa waangalizi tofauti kusonga jamaa na mtu mwingine, ingawa wote wawili ni katika muafaka inertial. Muda sahihi wa muda\(\Delta \tau\) kwa mwangalizi ambaye, kama astronaut, anahamia na vifaa, ni ndogo kuliko muda wa muda kwa waangalizi wengine. Ni ndogo iwezekanavyo kipimo wakati kati ya matukio mawili. Mwangalizi wa ardhi anaona vipindi vya muda ndani ya mfumo wa kusonga kama kupanuliwa (yaani, kupanuliwa) kuhusiana na jinsi mwangalizi anavyohamia jamaa na Dunia anavyowaona ndani ya mfumo wa kusonga. Vinginevyo, kwa mujibu wa mwangalizi wa ardhi, muda mdogo hupita kati ya matukio ndani ya sura inayohamia. Kumbuka kuwa muda mfupi uliopita kati ya matukio ni katika sura ya inertial ambayo mwangalizi anaona matukio (kwa mfano, chafu na kuwasili kwa ishara ya mwanga) hutokea kwa hatua moja.

Athari ya wakati huu ni halisi na haitoshi na saa zisizo sahihi au vipimo visivyofaa. Vipimo vya muda wa tukio hilo hutofautiana kwa waangalizi katika mwendo wa jamaa. Kupanua kwa muda ni mali ya ndani ya wakati yenyewe. Saa zote zinazohamia jamaa na mwangalizi, ikiwa ni pamoja na saa za kibaiolojia, kama vile moyo wa mtu, au kuzeeka, huzingatiwa kukimbia polepole zaidi ikilinganishwa na saa ambayo ni stationary jamaa na mwangalizi.

Kumbuka kwamba ikiwa kasi ya jamaa ni ndogo sana kuliko kasi ya nuru (v <<<c), basi\(v^2/c^2\) ni ndogo mno, na nyakati zilizopita\(\Delta t\) na\(\Delta \tau\) ni karibu sawa. Kwa kasi ya chini, fizikia inayotokana na mbinu za kisasa za relativity za fizikia za fizikia-kila siku zinahusisha madhara madogo sana ya relativistic Hata hivyo, kwa kasi karibu na kasi ya mwanga,\(v^2/c^2\) ni karibu na moja, hivyo\(\sqrt{1 - v^2/c^2}\) ni ndogo sana na\(\Delta t\) inakuwa kubwa zaidi kuliko\(\Delta \tau\).

Nusu ya maisha ya Muon

Kuna ushahidi mkubwa wa majaribio kwamba equation\(\Delta t = \gamma \Delta \tau\) ni sahihi. Mfano mmoja unapatikana katika chembe za ray za cosmic ambazo zinaendelea mvua chini duniani kutoka kwenye nafasi ya kina. Baadhi ya migongano ya chembe hizi na viini katika anga ya juu husababisha chembe za muda mfupi zinazoitwa muons. Nusu ya maisha (kiasi cha muda kwa nusu ya nyenzo kuoza) ya muoni ni 1.52 μs wakati inapumzika jamaa na mwangalizi anayepima nusu ya maisha. Hii ni wakati sahihi wakati\(\Delta \tau\). Muda mfupi huu unaruhusu muoni wachache sana kufikia uso wa Dunia na kugunduliwa kama mawazo ya Newton kuhusu wakati na nafasi yalikuwa sahihi. Hata hivyo, muoni zinazozalishwa na chembe za ray za cosmic zina kasi nyingi, huku baadhi ya kusonga karibu na kasi ya nuru. Imebainika kuwa nusu ya maisha ya muoni kama kipimo na mwangalizi wa ardhi (\(\Delta t\)) inatofautiana na kasi hasa kama ilivyotabiriwa na equation\(\Delta t = \gamma \Delta \tau\). Haraka ya mwezi huenda, inaishi tena. Sisi duniani tunaona muoni hudumu kwa muda mrefu zaidi kuliko nusu yake ya maisha inavyotabiri ndani ya sura yake ya kupumzika. Kama inavyotazamwa kutoka kwenye sura yetu, muon huharibika polepole zaidi kuliko inavyofanya wakati unapumzika kuhusiana na sisi. Sehemu kubwa zaidi ya muons hufikia chini kama matokeo.

Kabla ya kuwasilisha mfano wa kwanza wa kutatua tatizo katika relativity, tunasema mkakati unaweza kutumia kama mwongozo wa mahesabu haya.

MKAKATI WA KUTATUA TATIZO: UHUSIANO

Fanya orodha ya kile kinachopewa au kinaweza kuhitimishwa kutokana na tatizo kama ilivyoelezwa (kutambua maarifa). Angalia hasa kwa taarifa juu ya jamaa kasi v.
Tambua hasa kile kinachohitajika kuamua katika tatizo (kutambua haijulikani).
Kuhakikisha kuelewa mambo ya dhana ya tatizo kabla ya kufanya mahesabu yoyote (kueleza jibu kama equation). Chagua, kwa mfano, ambayo mwangalizi anaona muda uliopanuliwa au urefu ulioambukizwa kabla ya kufanya kazi na equations au kuitumia kutekeleza hesabu. Ikiwa umefikiri juu ya nani anayeona nini, ni nani anayehamia na tukio lililozingatiwa, ambaye anaona wakati unaofaa, na kadhalika, utapata rahisi zaidi kuamua kama hesabu yako ni ya busara.
Tambua aina ya msingi ya hesabu inayofanyika ili kupata haijulikani kutambuliwa hapo juu (fanya hesabu). Utapata sehemu muhtasari kusaidia katika kuamua kama urefu contraction, relativistic kinetic nishati, au baadhi dhana nyingine ni kushiriki.

Kumbuka kwamba haipaswi kuzunguka wakati wa hesabu. Kama ilivyoelezwa katika maandiko, lazima mara nyingi ufanyie mahesabu yako kwa tarakimu nyingi ili uone athari inayotaka. Unaweza kuzunguka mwishoni mwa ufumbuzi wa tatizo, lakini usitumie nambari iliyozunguka katika hesabu inayofuata. Pia, angalia jibu ili uone ikiwa ni busara: Je, ina maana? Hii inaweza kuwa ngumu zaidi kwa relativity, ambayo ina mifano michache ya kila siku kutoa uzoefu na kile kinachofaa. Lakini unaweza kuangalia kasi zaidi kuliko c au madhara ya relativistic ambayo iko katika mwelekeo sahihi (kama vile contraction wakati ambapo dilation ilitarajiwa).

Mfano\(\PageIndex{1A}\): Time Dilation in a High-Speed Vehicle

Gari la Teknolojia ya Hypersonic 2 (HTV-2) ni gari la roketi la majaribio linaloweza kusafiri saa 21,000 km/h (5830 m/s). Ikiwa saa ya umeme katika HTV-2 inapima muda wa muda wa muda wa 1-s, watazamaji duniani wataweza kupima muda wa muda kuwa nini?

Mkakati

Tumia formula ya kupanua wakati ili kuhusisha muda sahihi wa ishara katika HTV-2 kwa muda uliopimwa chini.

Suluhisho

Tambua maarifa:\(\Delta \tau = 1 \, s\);\(v = 5830m/s.\)
Tambua haijulikani:\(\Delta t\).
Eleza jibu kama equation:
\[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
Kufanya hesabu. Tumia usemi\(\gamma\) kwa kuamua\(\Delta t\) kutoka\(\Delta \tau\):
\[\begin{align*} \Delta t &= \dfrac{1 \, s}{\sqrt{1 - \left(\dfrac{5830 \, m/s}{3.00 \times 10^8 m/s}\right)^2}} \\[4pt] &= 1.000000000189 \, s \\[4pt] &= 1 \, s + 1.89 \times 10^{-10}s. \end{align*} \nonumber \]

Umuhimu

Kasi ya juu sana ya HTV-2 bado ni mara 10 ^-5 tu kasi ya mwanga. Madhara ya relativistic kwa HTV-2 ni duni kwa karibu madhumuni yote, lakini sio sifuri.

Nini kasi ni Relativistic?

Je! Gari linapaswa kusafiri kwa kasi kwa sekunde 1 ya muda kupimwa kwenye saa ya abiria katika gari ili kutofautiana na 1% kwa mwangalizi anayeipima kutoka ardhini nje?

Mkakati

Tumia formula ya kupanua wakati ili kupata v/c kwa uwiano uliopewa wa nyakati.

Suluhisho

Tambua inayojulikana:
\[\dfrac{\Delta \tau}{\Delta t} = \dfrac{1}{1.01}. \nonumber \]
Tambua haijulikani: v/c.
Eleza jibu kama equation:
\[ \begin{align*} \Delta t &= \gamma \Delta \tau \\[4pt] &= \dfrac{1}{\sqrt{1 - v^2/c^2}}\Delta \tau \\[4pt] \dfrac{\Delta \tau}{\Delta t} &= \sqrt{1 - v^2/c^2} \\[4pt] \left(\dfrac{\Delta \tau}{\Delta t}\right)^2 &= 1 - \dfrac{v^2}{c^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - (\Delta \tau/\Delta t)^2}. \end{align*} \nonumber \]
Je, hesabu:
\[\dfrac{v}{c} = \sqrt{1 - (1/1.01)^2} = 0.14. \nonumber \]

Umuhimu

Matokeo yanaonyesha kwamba kitu kinapaswa kusafiri kwa takribani 10% ya kasi ya mwanga kwa mwendo wake ili kuzalisha madhara makubwa ya kupungua kwa muda wa relativistic.

Kuhesabu\(\Delta t\) kwa Tukio la Relativistic

Tuseme ray ya cosmic inayogongana na kiini katika anga ya juu ya Dunia inazalisha muoni ambayo ina kasi\(v = 0.950c\). Muon kisha husafiri kwa kasi ya mara kwa mara na huishi 2.20 μs kama ilivyopimwa katika sura ya muon ya kumbukumbu. (Unaweza kufikiria hili kama saa ya ndani ya muon.) Muon huishi muda gani kama kipimo na mwangalizi wa ardhi (Kielelezo\(\PageIndex{2}\))?

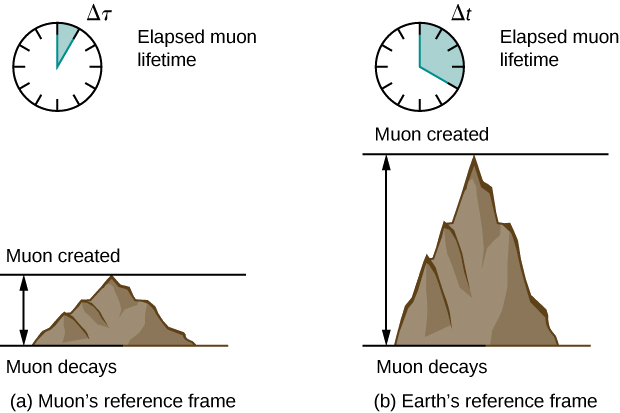
Kielelezo a, yenye kichwa “Muon ya kumbukumbu ya sura,” inaonyesha mchoro wa saa ya analog na muda wa muda uliovuliwa na kinachoitwa Delta tau. Saa inaitwa “Ilipita muon maisha”. Chini ya saa ni kuchora kwa mlima. Mstari wa usawa kwenye ngazi ya juu ya mlima huitwa “Muon imeundwa.” Mstari wa usawa chini ya mlima unaitwa “Muon kuoza.” Mshale wa mwisho wa wima unaonyesha umbali wa wima kati ya mistari hii. Kielelezo b ni jina la “sura ya kumbukumbu ya Dunia.” Inaonyesha mchoro wa saa Analog na muda muda kivuli na kinachoitwa Delta t. muda kivuli katika takwimu b ni kubwa kuliko muda katika takwimu a. saa kinachoitwa “Ilipita muon maisha”. Chini ya saa ni mchoro wa mlima ambao ni mrefu kuliko mlima katika kielelezo a. mstari usawa katika ngazi ya juu ya mlima ni kinachoitwa “Muon umba.” Mstari wa usawa chini ya mlima unaitwa “Muon kuoza.” Mshale wa mwisho wa wima unaonyesha umbali wa wima kati ya mistari hii. — Kielelezo\(\PageIndex{2}\): Muon katika anga ya Dunia huishi muda mrefu kama kipimo na mwangalizi wa ardhi kuliko ilivyopimwa na saa ya ndani ya muon.

Kama tutakavyojadili baadaye, katika sura ya kumbukumbu ya muon, inasafiri umbali mfupi kuliko kipimo katika sura ya kumbukumbu ya Dunia.

Mkakati

Saa inayohamia na muon inachukua muda mzuri wa mchakato wake wa kuoza, hivyo wakati tunapopewa ni\(\Delta \tau = 2.20 \mu s\). Earthbound mwangalizi hatua\(\Delta t\) kama iliyotolewa na equation\(\Delta t = \gamma \Delta \tau\). Kwa sababu kasi imetolewa, tunaweza kuhesabu muda katika sura ya kumbukumbu ya Dunia.

Suluhisho

Tambua maarifa:\(v = 0.950c\);\(\delta \tau = 2.20 \mu s\).
Tambua haijulikani:\(\Delta t\).
Eleza jibu kama equation. Tumia:
\[\Delta t = \gamma \Delta \tau. \nonumber \]
na
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
Kufanya hesabu. Tumia usemi\(\gamma\) kwa kuamua\(\Delta t\) kutoka\(\Delta \tau\):
\[\begin{align*} \Delta t &= \gamma \Delta \tau. \\[4pt] &=\dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}\delta \tau \\[4pt] &=\dfrac{2.20 \mu s}{\sqrt{1 - (0.950)^2}} \\[4pt] &= 7.05 \, \mu s.\end{align*} \nonumber \]
Kumbuka kuweka takwimu za ziada muhimu mpaka jibu la mwisho.

Umuhimu

Moja ya maana ya mfano huu ni kwamba kwa sababu\(\gamma = 3.20\) kwa 95.0% ya kasi ya mwanga (\(v = 0.950c\)), athari za relativistic ni muhimu. Vipindi viwili vya muda vinatofautiana na sababu ya 3.20, wakati wa kawaida wangekuwa sawa. Kitu kinachohamia saa 0.950 c kinasemekana kuwa relativistic sana.

Mfano\(\PageIndex{1B}\): Relativistic Television

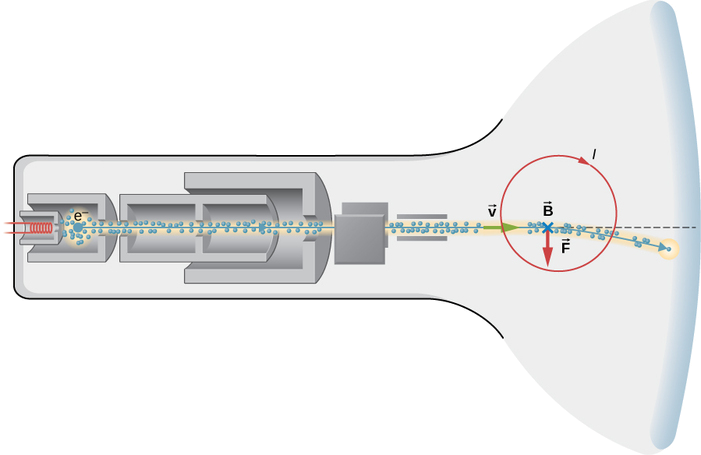
Screen isiyo ya gorofa, kuonyesha televisheni ya zamani (Kielelezo\(\PageIndex{3}\)) hufanya kazi kwa kuharakisha elektroni kwa umbali mfupi hadi kasi ya relativistic, na kisha kutumia mashamba ya umeme ili kudhibiti ambapo boriti ya elektroni inapiga safu ya umeme mbele ya bomba. Tuseme elektroni kusafiri\(6.00 \times 10^7 m/s\) kwa umbali wa 0.200m0.200m kutoka mwanzo wa boriti kwenye skrini.

Ni wakati gani wa kusafiri kwa elektroni katika sura iliyobaki ya kuweka televisheni?
Wakati wa elektroni wa kusafiri katika sura yake ya kupumzika ni nini?

Mfano wa maelezo ya ndani ya kuonyesha tube ya cathode ray inavyoonyeshwa. Katika mwisho mmoja wa bomba ni filament na wingu la elektroni ambazo ni collimated katika boriti usawa pamoja mhimili wa tube. Boriti ya elektroni kisha hupita kati ya sahani mbili za wima sambamba, halafu kati ya sahani mbili za usawa zinazofanana. Electron exit sahani na kasi v kulia na kuingia eneo magnetic uwanja B akizungumzia katika ukurasa, clockwise sasa mimi, na nguvu ya kushuka F. boriti ya elektroni hupungua chini katika eneo hili na hupiga mbele ya wima ya tube chini ya mhimili. — Kielelezo\(\PageIndex{3}\): boriti elektroni katika cathode ray tube televisheni kuonyesha.

Mkakati wa (a)

(a) Mahesabu ya muda kutoka\(vt = d\). Ingawa kasi ni relativistic, hesabu ni kabisa katika sura moja ya kumbukumbu, na kwa hiyo relativity si kushiriki.

Suluhisho

Tambua maarifa:
\[v = 6.00 \times 10^7 m/s \, d = 0.200 \, m. \nonumber \]
Tambua haijulikani: wakati wa kusafiri\(\Delta t\).
Eleza jibu kama equation:
\[\Delta t = \dfrac{d}{v}. \nonumber \]
Je, hesabu:
\[ \begin{align*} t &= \dfrac{0.200 \, m}{6.00 \times 10^7 \, m/s} \\[4pt] &= 3.33 \times 10^{-9} \, s. \end{align*} \nonumber \]

Umuhimu

Wakati wa kusafiri ni mfupi sana, kama inavyotarajiwa. Kwa sababu hesabu ni kabisa ndani ya sura moja ya kumbukumbu, relativity haihusiki, ingawa kasi ya elektroni iko karibu na c.

Mkakati wa (b)

(b) Katika sura ya kumbukumbu ya elektroni, tube ya utupu inahamia na elektroni imesimama. Cathode inayotokana na elektroni inaacha elektroni na mbele ya tube ya utupu hupiga elektroni na elektroni mahali pale. Kwa hiyo tunatumia formula ya kupanua muda ili kuhusisha wakati unaofaa katika sura ya kupumzika kwa elektroni kwa wakati katika sura ya televisheni.

Suluhisho

Tambua maarifa (kutoka sehemu a):
\[\Delta t = 3.33 \times 10^{-9} \, s; \, v = 6.00 \times 10^7 \, m/s; \, d = 0.200 \, m. \nonumber \]
Tambua haijulikani:\(\tau\).
Eleza jibu kama equation:
\[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - v^2/c^2}}. \nonumber \]
Je, hesabu:
\[\begin{align*} \Delta \tau &= (3.33 \times 10^{-9}s)\sqrt{1 - \left(\dfrac{6.00 \times 10^7 m/s}{3.00 \times 10^8 m/s}\right)^2} \\[4pt] &= 3.26 \times 10^{-9}s. \end{align*} \nonumber \]

Umuhimu

Wakati wa kusafiri ni mfupi katika sura ya elektroni ya kumbukumbu. Kwa sababu tatizo linahitaji kupata muda wa muda uliopimwa katika muafaka tofauti wa kumbukumbu kwa mchakato huo, uwiano unahusishwa. Ikiwa tulikuwa tumejaribu kuhesabu muda katika sura ya kupumzika ya elektroni kwa kugawanya tu 0.200 m kwa kasi, matokeo yatakuwa sahihi kidogo kwa sababu ya kasi ya relativistic ya elektroni.

Zoezi\(\PageIndex{1}\)

Ni nini\(\gamma\) kama\(v = 0.650c\)?

Jibu: \[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1}{\sqrt{1 - \dfrac{(0.650c)}{c^2}}} = 1.32 \nonumber \]

Twin Paradoksi

Matokeo ya kusisimua ya kupungua kwa muda ni kwamba msafiri wa nafasi anayehamia kwa kasi ya juu na Dunia angekuwa na umri mdogo kuliko pacha ya mwanaanga. Hii mara nyingi hujulikana kama kitendawili cha pacha. Fikiria astronaut kusonga kwa kasi kama hiyo\(\gamma = 30.0\), kama katika Kielelezo\(\PageIndex{4}\). Safari ambayo inachukua miaka 2.00 katika sura yake itachukua miaka 60.0 katika sura ya mapacha ya ardhi. Tuseme astronaut husafiri 1.00 mwaka kwa mfumo mwingine nyota, kwa ufupi inahusu eneo hilo, na kisha husafiri 1.00 mwaka nyuma. Mwanaanga ambaye alikuwa na umri wa miaka 40 mwanzoni mwa safari ingekuwa 42 wakati spaceship anarudi. Kila kitu duniani, hata hivyo, ingekuwa na umri wa miaka 60.0. Twin ya ardhi, ikiwa bado hai, ingekuwa na umri wa miaka 100.

Hali inaweza kuonekana tofauti na astronaut katika Kielelezo\(\PageIndex{4}\). Kwa sababu mwendo ni jamaa, spaceship itaonekana kuwa stationary na Dunia itaonekana kuhamia. (Hii ni hisia unayo wakati wa kuruka kwenye ndege.) Kuangalia nje ya dirisha la spaceship, astronaut bila kuona wakati polepole chini duniani kwa sababu ya\(\gamma = 30.0\). Kuonekana kutoka kwa spaceship, ndugu wa ardhi atakuwa na umri wa miaka 2/30 tu, au 0.07, ya mwaka, ambapo mwanaanga angekuwa na umri wa miaka 2.00.

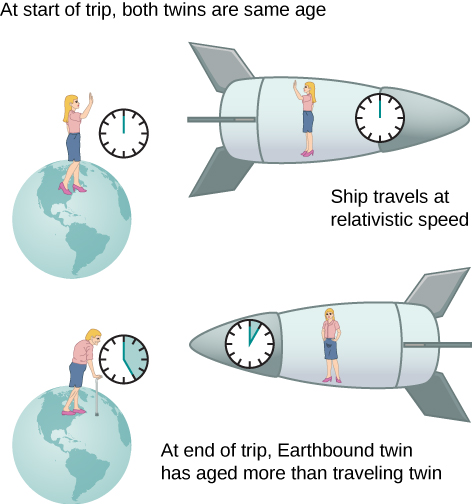
Kuna vielelezo viwili. Mfano wa kwanza unaitwa “Mwanzoni mwa safari, mapacha wote wawili wana umri uleule” na unaonyesha mmoja wa mapacha duniani na mwingine kwenye meli inayosafiri mbali na ardhi kwa kasi ya relativistic. Mapacha yote ni umri sawa, na kila mmoja ana saa. Saa zote mbili zinaonyesha wakati mmoja. Mfano wa pili umeandikwa “Mwishoni mwa safari, pacha ya Earthbound ina umri zaidi ya kusafiri pacha.” Mfano huu unaonyesha meli ikirudi nyuma duniani. Pacha kwenye meli inaonekana sawa na katika mfano wa kwanza na saa yake inaonyesha muda mfupi uliopita. Twin duniani ni mzee sana, na saa yake inaonyesha muda mrefu uliopita. — Kielelezo\(\PageIndex{4}\): Kitendawili cha mapacha kina hitimisho linalopingana kuhusu umri wa mapacha zaidi kutokana na safari ndefu ya nafasi kwa kasi ya relativistic.

Kitendawili hapa ni kwamba mapacha mawili hayawezi kuwa sahihi. Kama ilivyo na paradoxes zote, hitimisho zinazopingana zinatoka kwenye Nguzo ya uongo. Kwa kweli, mwendo wa astronaut ni tofauti sana na ule wa mapacha ya ardhi. Mwanaanga huharakisha hadi kasi ya juu na kisha hupungua ili kuona mfumo wa nyota. Ili kurudi duniani, yeye huharakisha tena na kupungua. Spacecraft si katika sura moja inertial ambayo formula wakati dilation inaweza kutumika moja kwa moja. Hiyo ni, mapacha ya astronaut hubadilisha marejeo ya inertial. Twin ya ardhi haipatikani kasi hizi na inabakia katika sura sawa ya inertial. Kwa hiyo, hali hiyo sio sawa, na si sahihi kudai kwamba astronaut anaona madhara sawa na pacha yake. Ukosefu wa ulinganifu kati ya mapacha utakuwa dhahiri zaidi wakati sisi kuchambua safari baadaye katika sura hii katika suala la njia astronaut ifuatavyo kwa njia ya nne-dimensional nafasi wakati.

Mwaka 1971, Wafizikia wa Marekani Joseph Hafele na Richard Keating walithibitisha kupungua kwa muda kwa kasi ya chini ya jamaa kwa kuruka saa za atomiki sahihi sana duniani kote kwenye ndege za kibiashara. Walipima muda uliopita kwa usahihi wa nanoseconds chache na kulinganisha na muda uliopimwa na saa zilizoachwa nyuma. Matokeo ya Hafele na Keating yalikuwa ndani ya uhakika wa majaribio ya utabiri wa relativity. Uhusiano wa pekee na wa jumla ulipaswa kuzingatiwa, kwa sababu mvuto na kasi zilihusika pamoja na mwendo wa jamaa.

Zoezi\(\PageIndex{2A}\)

a. chembe husafiri katika\(1.90 \times 10^8 \, m/s\) na maisha\(2.1 \times 10^8 \, s\) wakati katika mapumziko jamaa na mwangalizi. Je, chembe huishi kwa muda gani kama inavyoonekana katika maabara?

Jibu: \[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{2.10 \times 10^{-8}s}{\sqrt{1 - \dfrac{(1.90 \times 10^8 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 2.71 \times 10^{-8} \, s. \nonumber \]

Zoezi\(\PageIndex{2B}\)

Spacecraft A na B kupita katika pande kinyume katika kasi ya jamaa ya\(4.00 \times 10^7 \, m/s\). Saa ya ndani katika spacecraft A husababisha emit ishara ya redio kwa 1.00 s. kompyuta katika spacecraft B hurekebisha kwa mwanzo na mwisho wa ishara baada ya kusafiri umbali tofauti, kuhesabu muda wakati ambapo meli A ilikuwa ikitoa ishara. Ni muda gani ambao kompyuta katika spacecraft B huhesabu nini?

Jibu

Ni kasi tu ya jamaa ya spacecraft mbili mambo kwa sababu hakuna mwendo kamili kupitia nafasi. Ishara imetolewa kutoka eneo lililowekwa katika sura ya kumbukumbu ya A, hivyo muda sahihi wa muda wa chafu yake ni\(\tau = 1.00 \, s\). Muda wa ishara iliyopimwa kutoka kwa sura ya kumbukumbu B ni basi

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1.00 \, s}{\sqrt{1 - \dfrac{(4.00 \times 10^7 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 1.01 \, s. \nonumber \]