2.4: Picha zilizoundwa na kukataa

Last updated
Save as PDF

Page ID: 175738

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Eleza malezi ya picha kwa uso mmoja wa kukataa
Tambua eneo la picha na uhesabu mali zake kwa kutumia mchoro wa ray
Tambua eneo la picha na uhesabu mali zake kwa kutumia equation kwa uso mmoja wa kukataa

Wakati mionzi ya mwanga inapoenea kutoka katikati hadi nyingine, mionzi hii inakabiliwa na kukataa, ambayo ni wakati mawimbi ya mwanga yanapigwa kwenye interface kati ya vyombo vya habari viwili. Nguvu ya kukataa inaweza kuunda picha kwa namna sawa na uso wa kutafakari, isipokuwa kwamba sheria ya kukataa (sheria ya Snell) iko katikati ya mchakato badala ya sheria ya kutafakari.

Kukataa kwenye Kiolesura cha Ndege-Kina cha Dhahiri

Ikiwa unatazama fimbo moja kwa moja iliyoingia ndani ya maji, inaonekana kuinama kwenye uso. Sababu ya athari hii ya curious ni kwamba sura ya fimbo ndani ya maji huunda karibu kidogo na uso kuliko nafasi halisi ya fimbo, kwa hiyo haina mstari na sehemu ya fimbo iliyo juu ya maji. Sifa hiyo inaelezea kwa nini samaki katika maji inaonekana kuwa karibu na uso kuliko ilivyo kweli.

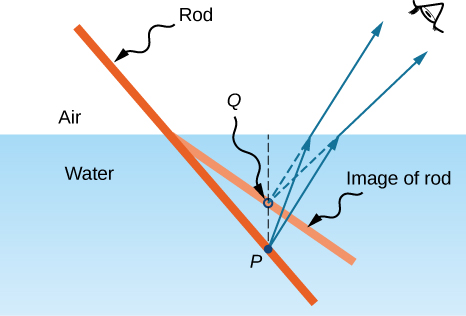
Kielelezo kinaonyesha mtazamo wa upande wa fimbo iliyoingizwa ndani ya maji. Mstari mwepesi ulioitwa picha ya fimbo unaonyeshwa kwa namna ambayo inaonekana kama fimbo imefungwa kwenye makutano ya hewa na maji. Point P ni juu ya fimbo na uhakika Q ni juu ya sura ya fimbo. Mstari wa PQ unaonyeshwa perpendicular kwa uso wa maji. Mionzi miwili hutoka P, kusafiri hadi juu ya uso wa maji, bend kwa pembe na kufikia jicho la mwangalizi. Upanuzi wa nyuma wa mionzi ya bent inaonekana kutoka hatua ya Q. — Kielelezo\(\PageIndex{1}\): Kupigwa kwa fimbo kwenye interface ya maji-hewa. Point\(P\) juu ya fimbo inaonekana kuwa katika hatua\(Q\), ambayo ni ambapo picha ya hatua P fomu kutokana na refraction katika interface hewa-maji.

Ili kujifunza malezi ya picha kama matokeo ya kukataa, fikiria maswali yafuatayo:

Ni nini kinachotokea kwa mionzi ya mwanga wakati wanapoingia au hupita katikati tofauti?
Je! Mionzi iliyofutwa inayotokana na hatua moja hukutana wakati fulani au hutengana mbali?

Ili kuwa halisi, tunazingatia mfumo rahisi unao na vyombo vya habari viwili vinavyotengwa na interface ya ndege (Kielelezo\(\PageIndex{2}\)). Kitu ni katikati moja na mwangalizi ni mwingine. Kwa mfano, unapoangalia samaki kutoka juu ya uso wa maji, samaki ni katikati ya 1 (maji) na index ya refractive 1.33, na jicho lako liko katikati ya 2 (hewa) na index ya refractive 1.00, na uso wa maji ni interface. Ya kina ambacho “unaona” ni urefu wa picha\(h_i\) na huitwa kina cha wazi. Kina halisi cha samaki ni urefu wa kitu\(h_o\).

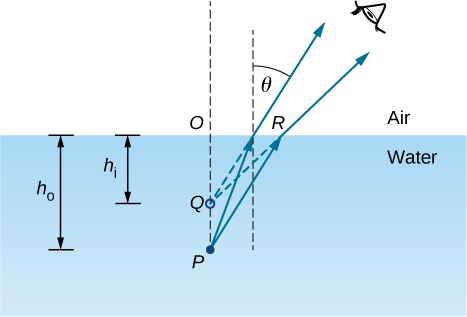
Kielelezo kinaonyesha mtazamo wa upande wa kiasi fulani cha maji. Point P iko ndani yake. Mionzi miwili hutoka kwenye hatua ya P, bend juu ya uso wa maji na kufikia jicho la mwangalizi. Upanuzi nyuma ya rays hizi refracted intersect katika hatua Q. PQ ni perpendicular kwa uso wa maji na intersects yake katika hatua O. umbali OP ni kinachoitwa h subscript o na umbali OQ ni kinachoitwa h subscript i. angle sumu na ray refracted na mstari perpendicular kwa uso wa maji ni kinachoitwa theta. — Kielelezo\(\PageIndex{2}\): Inaonekana kina kutokana na kukataa. Kitu halisi katika hatua P inajenga picha katika hatua ya Swali. Picha si kwa kina sawa na kitu, hivyo mwangalizi anaona picha katika “kina dhahiri.”

Kina cha wazi h _i inategemea angle ambayo unaona picha. Kwa mtazamo kutoka juu (kinachojulikana “kawaida” mtazamo), tunaweza takriban refraction angle\(θ\) kuwa ndogo, na kuchukua nafasi\(\sin θ\) katika sheria Snell na\(\tan θ\). Kwa makadirio haya, unaweza kutumia pembetatu\(ΔOPR\) na\(ΔOQR\) kuonyesha kwamba kina cha dhahiri kinatolewa na

\[h_i= \left(\dfrac{n_2}{n_1}\right)h_o. \nonumber \]

Kupatikana kwa matokeo haya ni kushoto kama zoezi. Hivyo, samaki huonekana kwenye 3/4 ya kina halisi inapotazamwa kutoka hapo juu.

Kukataa kwenye Interface ya Spherical

Maumbo ya spherical yana jukumu muhimu katika optics hasa kwa sababu maumbo ya spherical ya ubora ni rahisi sana kutengeneza kuliko nyuso zingine zilizopigwa. Ili kujifunza kukataa kwenye uso mmoja wa spherical, tunadhani kwamba kati na uso wa spherical mwisho mmoja unaendelea kwa muda usiojulikana (katikati “isiyo na mwisho”).

Kukataa kwenye uso wa Convex

Fikiria chanzo cha mwanga kwenye hatua ya P mbele ya uso wa mbonyeo uliofanywa kwa kioo (Kielelezo\(\PageIndex{3}\)). Hebu\(R\) kuwa radius ya curvature, n ₁ kuwa index refractive ya kati ambayo kitu uhakika P iko, na n ₂ kuwa index refractive ya kati na uso spherical. Tunataka kujua kinachotokea kama matokeo ya kukataa kwenye interface hii.

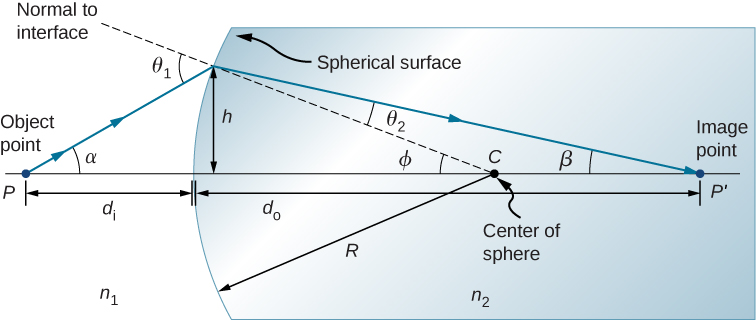
Kielelezo kinaonyesha sehemu ya nyanja. Refractive index ya hewa ni n subscript 1 na ile ya nyanja ni n subscript 2. Kituo cha nyanja ni C na radius ni R. ray inayotoka hatua P juu ya mhimili macho nje ya nyanja mgomo mbonyeo uso wa nyanja na ni refracted ndani yake. Ni intersects mhimili katika hatua P mkuu ndani ya nyanja, upande wa pili wa kituo. Mstari wa dotted unaoitwa kawaida kwa interface unaunganisha katikati ya nyanja hadi hatua ya matukio. Inafanya phi ya angle na mhimili wa macho. Tukio hilo na mionzi iliyokataliwa hufanya pembe alpha na beta mtawalia na mhimili wa macho na pembe theta 1 na theta 2 mtawalia na kawaida kwa interface. — Kielelezo\(\PageIndex{3}\): Kukataa kwenye uso wa convex (\(n_2>n_1\)).

Kwa sababu ya ulinganifu unaohusika, inatosha kuchunguza mionzi katika ndege moja tu. Takwimu inaonyesha mwanga wa mwanga unaoanza kwenye hatua ya kitu\(P\), inakataza kwenye interface, na huenda kupitia hatua ya picha\(P′\). Tunapata formula inayohusiana na umbali wa kitu\(d_o\), umbali wa picha\(d_i\), na radius ya curvature\(R\).

Kutumia sheria Snell kwa ray inayotoka hatua\(P\) anatoa

\[n_1\sin θ_1=n_2 \sin θ_2. \nonumber \]

Ndani ya makadirio ndogo-angle

\[\sin θ≈θ, \nonumber \]

Sheria Snell kisha inachukua fomu

\[n_1θ_1≈n_2θ_2. \label{eq8} \]

Kutoka jiometri ya Kielelezo\(\PageIndex{3}\), tunaona kwamba

\[θ_1=α+ϕ, \nonumber \]

\[θ_2=ϕ−β. \nonumber \]

Kuingiza maneno yote katika Equation\ ref {eq8} inatoa

\[n_1(α+ϕ)≈n_2(ϕ−β). \label{eq10} \]

Kutumia Kielelezo\(\PageIndex{3}\), tunahesabu tangent ya pembe\(α\),\(β\), na\(ϕ\):

\(\tan α≈\dfrac{h}{d_o}\)
\(\tan β≈\dfrac{h}{d_i}\)
\(\tan ϕ≈\dfrac{h}{R}\)

Tena kwa kutumia makadirio ndogo-angle, tunaona kwamba\(\tan θ≈ θ\), hivyo mahusiano hapo juu kuwa

\(α≈\dfrac{h}{d_o}\)
\(~β≈\dfrac{h}{d_i}\)
\(~ϕ≈\dfrac{h}{R}.\)

Kuweka pembe hizi katika Equation\ ref {eq10} anatoa

\[n_1\left(\dfrac{h}{d_o}+\dfrac{h}{R}\right)=n_2 \left(\dfrac{h}{R}−\dfrac{h}{d_i}\right). \nonumber \]

Tunaweza kuandika hii kwa urahisi zaidi kama

\[\dfrac{n_1}{d_o}+\dfrac{n_2}{d_i}=\dfrac{n_2−n_1}{R}. \label{eq20} \]

Ikiwa kitu kinawekwa kwenye hatua maalum inayoitwa lengo la kwanza, au lengo la kitu\(F_1\), basi picha huundwa kwa infinity, kama inavyoonekana kwenye Mchoro\(\PageIndex{4a}\).

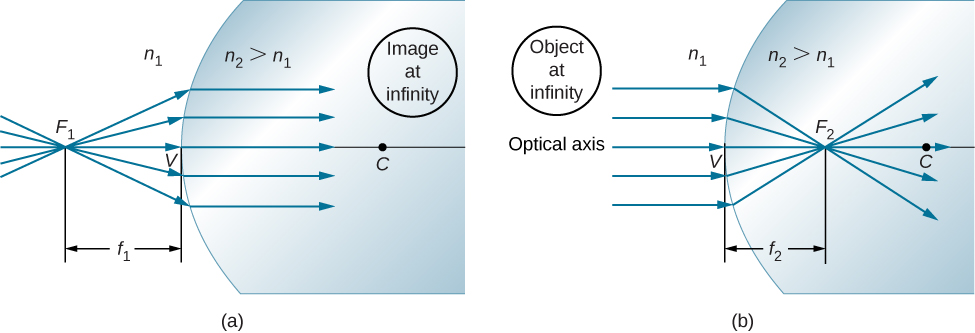
Kielelezo a inaonyesha sehemu ya nyanja na uhakika F1 nje yake, kwenye mhimili wa macho. Rays inayotoka F1 hupiga uso wa mbonyeo na hufutwa ndani ya nyanja kama mionzi inayofanana. Umbali wa F1 kutoka kwenye uso ni f subscript 1. Kielelezo b inaonyesha rays sambamba na mhimili macho akipiga uso convex na kuwa refracted. Wao hujiunga kwenye hatua ya F2 ndani ya nyanja. F2 iko juu ya mhimili wa macho kati ya uso na katikati ya nyanja. Umbali wa F2 kutoka kwenye uso ni f subscript 2. Katika takwimu zote mbili index refractive ya hewa ni n1 na ile ya nyanja ni n2 kubwa kuliko n1. — Kielelezo\(\PageIndex{4}\): (a) Mtazamo wa kwanza (unaoitwa “lengo la kitu”) kwa kukataa kwenye uso wa mchanganyiko. (b) Mtazamo wa pili (unaoitwa “mtazamo wa picha”) kwa kukataa kwenye uso wa mbonyeo.

Tunaweza kupata eneo la lengo\(f_1\) la kwanza\(F_1\) kwa kuweka\(d_i=\infty\) katika Equation\ ref {eq20}.

\[ \begin{align} \dfrac{n_1}{f_1}+\dfrac{n_2}{\infty} &=\dfrac{n_2−n_1}{R} \\[4pt] f_1 &=\dfrac{n_1R}{n_2−n_1} \end{align} \nonumber \]

Vile vile, tunaweza kufafanua lengo la pili au\(F_2\) mtazamo wa picha ambapo picha hutengenezwa kwa kitu ambacho ni mbali (Kielelezo\(\PageIndex{4b}\)). Eneo la lengo la pili\(F_2\) linapatikana kutoka Equation\ ref {eq20} kwa kuweka\(d_0=\infty\):

\[ \begin{align} \dfrac{n_1}{\infty}+\dfrac{n_2}{f_2}=\dfrac{n_2−n_1}{R} \\[4pt] f_2=\dfrac{n_2R}{n_2−n_1}. \end{align} \nonumber \]

Kumbuka kuwa lengo kitu ni katika umbali tofauti na kipeo kuliko lengo picha kwa sababu\(n_1≠n_2\).

Ishara mkataba kwa nyuso moja refracting

Ingawa sisi inayotokana equation hii kwa refraction katika uso mbonyeo, kujieleza huo ana kwa uso concave, mradi sisi kutumia zifuatazo ishara mkataba:

\(R>0\)kama uso ni mbonyeo kuelekea kitu; vinginevyo,\(R<0\).
\(d_i>0\)ikiwa picha ni halisi na upande wa pili kutoka kwa kitu; vinginevyo,\(d_i<0\).