2.5: Lenses nyembamba

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Tumia michoro ya ray ili kupata na kuelezea picha iliyoundwa na lens
• Tumia equation nyembamba-lens kuelezea na Machapisho picha iliyoundwa na lens

Lenses hupatikana katika safu kubwa ya vyombo vya macho, kuanzia kioo rahisi cha kukuza hadi lens ya zoom ya kamera hadi jicho yenyewe. Katika sehemu hii, tunatumia sheria ya Snell kuchunguza mali ya lenses na jinsi wanavyounda picha.

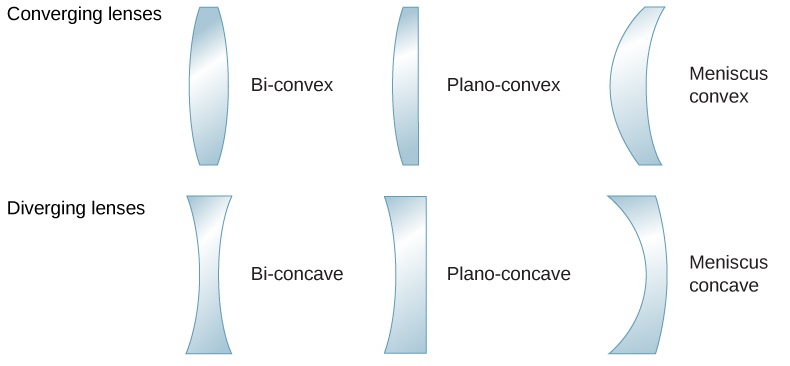
Neno “lens” linatokana na neno la Kilatini kwa maharagwe ya lenti, sura ambayo ni sawa na lens ya convex. Hata hivyo, si lenses zote zina sura sawa. Kielelezo\(\PageIndex{1}\) kinaonyesha aina mbalimbali za maumbo tofauti ya lens. Msamiati unaotumiwa kuelezea lenses ni sawa na ile iliyotumiwa kwa vioo vya spherical: Mhimili wa ulinganifu wa lens huitwa mhimili wa macho, ambapo mhimili huu unaingiliana uso wa lens huitwa kipeo cha lens, na kadhalika.

Kielelezo\(\PageIndex{1}\): Aina mbalimbali za lenses: Kumbuka kuwa lens inayogeuka ina “kiuno” kikubwa, wakati lens inayojitokeza ina kiuno nyembamba.

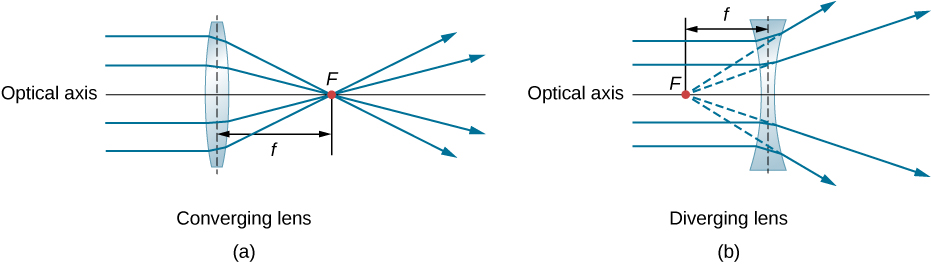
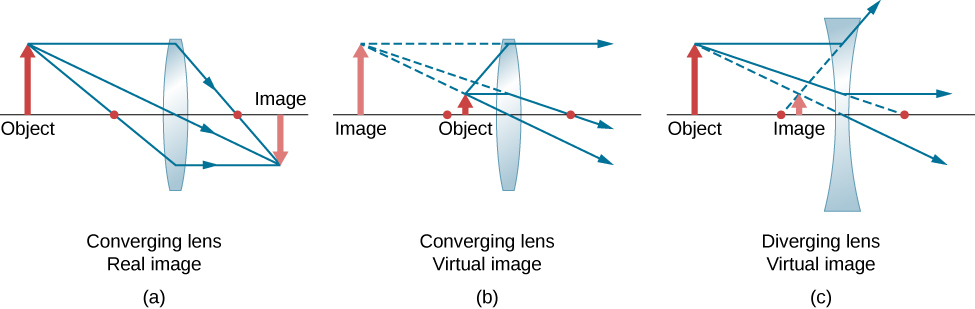
Mbonyeo au converging Lens ni umbo ili rays wote mwanga kwamba kuingia ni sambamba na mhimili wake macho intersect (au lengo) katika hatua moja juu ya mhimili macho upande wa pili wa lens, kama inavyoonekana katika Kielelezo\(\PageIndex{1a}\). Vivyo hivyo, lenzi ya concave au diverging imeumbwa ili mionzi yote inayoingia ndani yake sambamba na mhimili wake wa macho ikatengana, kama inavyoonekana katika sehemu (b). Ili kuelewa kwa usahihi jinsi lens inavyotumia mwanga, angalia kwa karibu kwenye ray ya juu ambayo inakwenda kupitia lens inayobadilika kwa sehemu (a). Kwa sababu index ya kukataa kwa lens ni kubwa zaidi kuliko ile ya hewa, sheria ya Snell inatuambia kwamba ray inakabiliwa na perpendicular kwa interface kama inaingia lens. Vivyo hivyo, wakati ray inapoondoka kwenye lens, inakabiliwa na perpendicular. hoja hiyo inatumika kwa lenses diverging, kama inavyoonekana katika Kielelezo \(\PageIndex{1b}\). Athari ya jumla ni kwamba mionzi ya mwanga ni bent kuelekea mhimili macho kwa lens converging na mbali na mhimili macho kwa lenses diverging. Kwa lens inayobadilika, hatua ambayo msalaba wa mionzi ni hatua ya F ya lens. Kwa lens inayojitokeza, hatua ambayo mionzi inaonekana inatoka ni hatua ya msingi (virtual). Umbali kutoka katikati ya lens hadi hatua yake ya msingi ni urefu wa focal f ya lens.

Kielelezo\(\PageIndex{2}\): Rays mwanga kuingia (a) converging Lens na (b) diverging Lens, sambamba na mhimili wake, hukutana katika focal yake F. umbali kutoka katikati ya Lens kwa focal ni lens focal urefu f Kumbuka kuwa mwanga rays ni bent juu ya kuingia na exiting Lens, na athari ya jumla kuwa bend rays kuelekea mhimili macho.

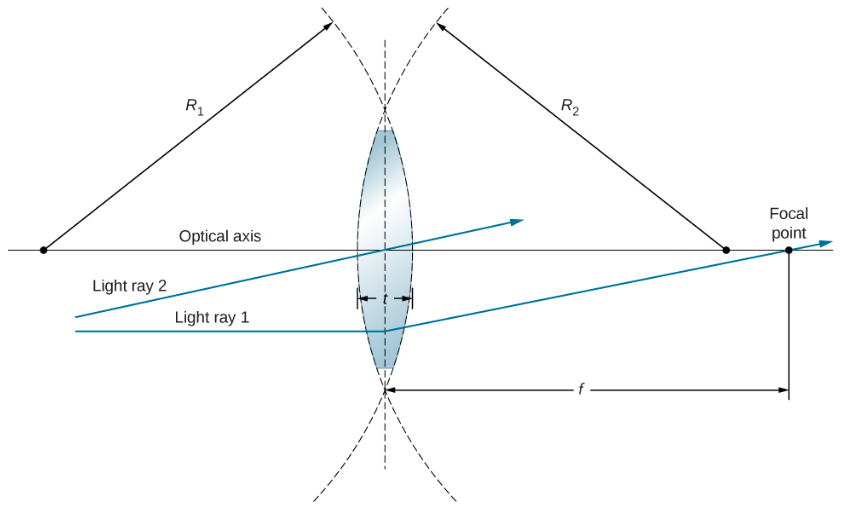
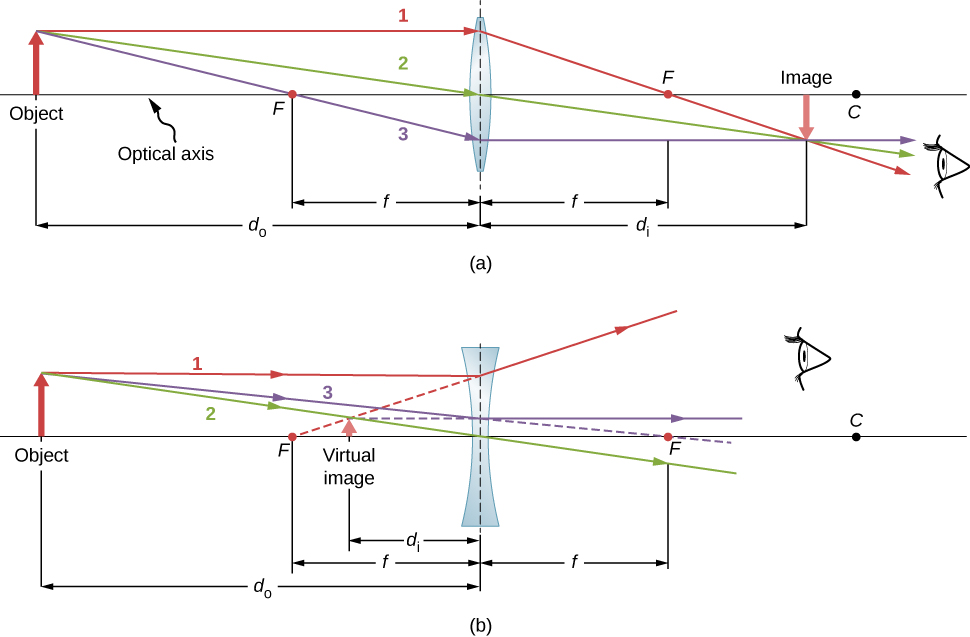
Lens inachukuliwa kuwa nyembamba ikiwa unene wake ni chini sana kuliko radii ya curvature ya nyuso zote mbili, kama inavyoonekana katika Kielelezo\(\PageIndex{3}\). Katika kesi hiyo, mionzi inaweza kuchukuliwa kuinama mara moja katikati ya lens. Kwa kesi inayotolewa katika takwimu, mwanga ray 1 ni sawa na mhimili wa macho, hivyo ray anayemaliza muda wake hupigwa mara moja katikati ya lens na huenda kupitia hatua ya msingi. Tabia nyingine muhimu ya lenses nyembamba ni kwamba mionzi ya mwanga ambayo hupita katikati ya lens haipatikani, kama inavyoonekana na mwanga wa mwanga 2.

Kielelezo\(\PageIndex{3}\): Katika makadirio nyembamba-lens, unene t wa lens ni mengi, chini ya radii R ₁ na R ₂ ya curvature ya nyuso za lens. Mionzi ya mwanga huchukuliwa kuinama katikati ya lens, kama vile mwanga wa mwanga 1. Mwanga wa mwanga 2 hupita katikati ya lens na hauwezi kupunguzwa katika makadirio nyembamba-lens.

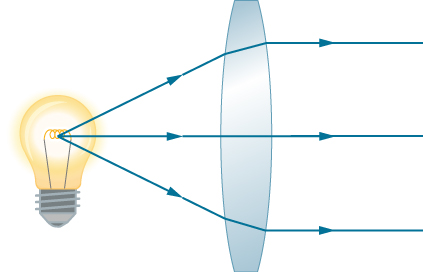
Kama ilivyoelezwa katika majadiliano ya awali ya sheria ya Snell, njia za mionzi ya mwanga zinabadilishwa kabisa. Hii ina maana kwamba mwelekeo wa mishale inaweza kuachwa kwa wote wa rays katika Kielelezo \(\PageIndex{2}\). Kwa mfano, ikiwa chanzo cha nuru kinawekwa kwenye kituo cha msingi cha lens ya mbonyeo, kama inavyoonekana kwenye Mchoro \(\PageIndex{4}\), mionzi ya mwanga inayofanana hutoka upande mwingine.

Kielelezo\(\PageIndex{4}\) katika lenses converging na diverging. Mbinu hii hutumiwa katika vituo vya taa na wakati mwingine katika taa za trafiki ili kuzalisha boriti ya mwanga kutoka chanzo kinachotoa mwanga kwa pande zote.

Ray Kufuatilia na Lenses nyembamba

Ufuatiliaji wa Ray ni mbinu ya kuamua au kufuata (kufuatilia) njia zilizochukuliwa na mionzi ya mwanga. Ray kufuatilia kwa lenses nyembamba ni sawa na mbinu tuliyotumia kwa vioo vya spherical. Kama kwa vioo, kufuatilia ray kunaweza kuelezea kwa usahihi uendeshaji wa lens. Sheria za kufuatilia ray kwa lenses nyembamba ni sawa na zile za vioo vya spherical:

1. Ray inayoingia kwenye lens inayobadilika sambamba na mhimili wa macho hupita kupitia hatua kuu upande wa pili wa lens (ray 1 katika sehemu (a) ya Kielelezo\(\PageIndex{4}\)). Ray inayoingia kwenye lens inayojitokeza sambamba na mhimili wa macho hutoka kwenye mstari unaopita kupitia hatua ya msingi upande mmoja wa lens (ray 1 katika sehemu (b) ya takwimu).
2. Ray inayopita katikati ya ama kugeuka au lens ya kugeuza haipatikani (ray 2 katika sehemu (a) na (b)).
3. Kwa lens inayobadilika, ray ambayo hupita kupitia hatua ya msingi hutoka lens sambamba na mhimili wa macho (ray 3 katika sehemu (a)). Kwa lens inayotofautiana, ray ambayo inakaribia kando ya mstari unaopita kupitia hatua ya juu upande wa pili hutoka lens sambamba na mhimili (ray 3 katika sehemu (b)).

Kielelezo\(\PageIndex{5}\): Lenses nyembamba na urefu sawa focal upande wowote. (a) Mionzi ya mwanga inayoingia kwenye lens inayobadilika kutoka msalaba wa kulia kwenye hatua yake ya kushoto. (b) Mionzi ya mwanga inayoingia kwenye lens inayojitokeza kutoka kulia inaonekana inatoka kwenye kitovu cha kulia.

Lenses nyembamba hufanya kazi vizuri kwa mwanga wa monochromatic (yaani, mwanga wa wavelength moja). Hata hivyo, kwa mwanga ambao una wavelengths kadhaa (kwa mfano, mwanga mweupe), lenses hufanya kazi vizuri sana. Tatizo ni kwamba, kama tulivyojifunza katika sura iliyotangulia, ripoti ya kukataa kwa nyenzo inategemea urefu wa mwanga. Jambo hili linawajibika kwa madhara mengi ya rangi, kama vile upinde wa mvua. Kwa bahati mbaya, jambo hili pia linasababisha kutofautiana katika picha zilizoundwa na lenses. Hasa, kwa sababu umbali wa lens hutegemea index ya kukataa, pia inategemea wavelength ya mwanga wa tukio hilo. Hii ina maana kwamba mwanga wa wavelengths tofauti utazingatia pointi tofauti, na kusababisha kinachojulikana kama “uharibifu wa chromatic.” Hasa, kando ya picha ya kitu nyeupe itakuwa rangi na kibaya. Lenses maalum zinazoitwa doublets zina uwezo wa kurekebisha uharibifu wa chromatic. Doublet hutengenezwa kwa gluing pamoja lens inayobadilika na lens diverging. Lens ya doublet ya pamoja inazalisha upungufu wa chromatic kwa kiasi kikubwa.

Uundaji wa picha na Lenses nyembamba

Tunatumia kufuatilia ray kuchunguza aina tofauti za picha ambazo zinaweza kuundwa kwa lens. Katika hali fulani, lens huunda picha halisi, kama vile wakati mradi wa filamu unapiga picha kwenye skrini. Katika hali nyingine, picha ni picha halisi, ambayo haiwezi kupangwa kwenye skrini. Ambapo, kwa mfano, ni picha iliyoundwa na miwani? Tunatumia ray kufuatilia kwa lenses nyembamba kuonyesha jinsi wao kuunda picha, na kisha sisi kuendeleza equations kuchambua quantitatively mali ya lenses nyembamba.

Fikiria kitu umbali mbali na lens converging, kama inavyoonekana katika Kielelezo\(\PageIndex{6}\). Ili kupata eneo na ukubwa wa picha, tunaelezea njia za mionzi ya mwanga iliyochaguliwa inayotoka kwenye hatua moja kwenye kitu, katika kesi hii, ncha ya mshale. Takwimu inaonyesha mionzi mitatu kutoka kwenye mionzi mingi inayotoka kwenye ncha ya mshale. Mionzi hii mitatu inaweza kufuatiliwa kwa kutumia sheria za kufuatilia ray zilizotolewa hapo juu.

• Ray 1 inaingia lens sambamba na mhimili wa macho na hupita kupitia hatua ya juu upande wa pili (utawala 1).
• Ray 2 hupita katikati ya lens na haipatikani (utawala wa 2).
• Ray 3 hupita kupitia hatua kuu juu ya njia yake ya lens na hutoka lens sambamba na mhimili wa macho (utawala wa 3).

Mionzi mitatu inavuka kwa hatua moja upande wa pili wa lens. Hivyo, picha ya ncha ya mshale iko katika hatua hii. Mionzi yote inayotoka kwenye ncha ya mshale na kuingia lens huvunjika na kuvuka kwenye hatua iliyoonyeshwa.

Baada ya kupata picha ya ncha ya mshale, tunahitaji hatua nyingine ya picha ili kuelekeza picha nzima ya mshale. Tulichagua kupata msingi wa picha wa mshale, ulio kwenye mhimili wa macho. Kama ilivyoelezwa katika sehemu ya vioo vya spherical, msingi utakuwa kwenye mhimili wa macho tu juu ya picha ya ncha ya mshale (kutokana na ulinganifu wa chini wa lens). Hivyo, picha inazunguka mhimili wa macho kwa urefu (hasi) umeonyeshwa. Mionzi kutoka kwenye hatua nyingine kwenye mshale, kama katikati ya mshale, msalaba kwenye hatua nyingine ya kawaida, hivyo kujaza picha nzima.

Ingawa mionzi mitatu inatajwa katika takwimu hii, mbili tu ni muhimu kupata hatua ya picha. Ni bora kufuatilia mionzi ambayo kuna sheria rahisi za kufuatilia ray.

Kielelezo\(\PageIndex{6}\): Ray kufuatilia hutumiwa Machapisho picha iliyoundwa na lens. Rays inayotokana na hatua hiyo juu ya kitu ni kufuatiliwa-rays tatu waliochaguliwa kila kufuata moja ya sheria kwa ray kufuatilia, ili njia zao ni rahisi kuamua. Picha iko kwenye hatua ambapo mionzi inavuka. Katika kesi hii, picha halisi - moja ambayo inaweza kuwa makadirio juu ya screen-ni sumu.

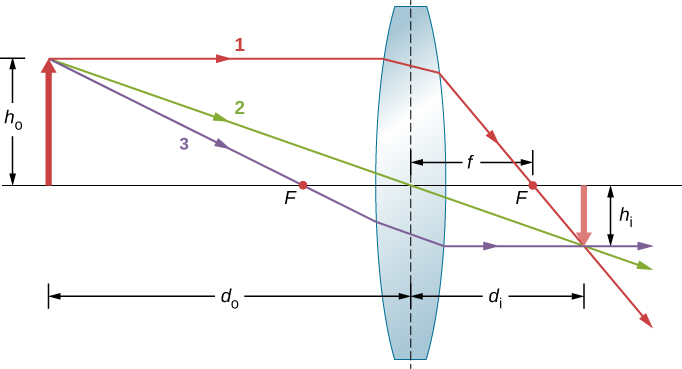
Umbali kadhaa muhimu huonekana katika takwimu. Kama kwa kioo, tunafafanua dodo kuwa umbali wa kitu, au umbali wa kitu kutoka katikati ya lens. Umbali wa picha d _i hufafanuliwa kuwa umbali wa picha kutoka katikati ya lens. Urefu wa kitu na urefu wa picha huonyeshwa na h _o na h _i, kwa mtiririko huo. Picha zinazoonekana sawa na kitu zina urefu mzuri, na wale ambao huingizwa wana urefu usiofaa. Kwa kutumia sheria za kufuatilia ray na kufanya kuchora wadogo na karatasi na penseli, kama hiyo katika Kielelezo \(\PageIndex{6}\), tunaweza kuelezea kwa usahihi eneo na ukubwa wa picha. Lakini faida halisi ya kufuatilia ray ni katika kutazama jinsi picha zinavyoundwa katika hali mbalimbali.

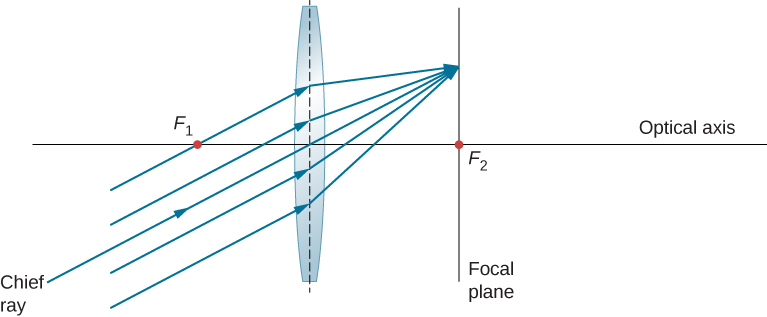
Oblique Sambamba Rays na Ndege

Tumeona kwamba mionzi inayofanana na mhimili wa macho huelekezwa kwenye sehemu kuu ya lens inayobadilika. Katika kesi ya lens inayotofautiana, hutoka katika mwelekeo kama vile wanaonekana kuwa wanatoka kwenye kituo cha juu upande wa pili wa lens (yaani, upande ambao mionzi inayofanana huingia kwenye lens). Ni nini kinachotokea kwa mionzi inayofanana ambayo si sawa na mhimili wa macho (Kielelezo \(\PageIndex{7}\))? Katika kesi ya lens inayobadilika, mionzi hii haipatikani kwenye hatua ya msingi. Badala yake, wao kuja pamoja juu ya hatua nyingine katika ndege inayoitwa ndege focal. Ndege ya msingi ina kipaumbele na ni perpendicular kwa mhimili wa macho. Kama inavyoonekana katika takwimu, mionzi inayofanana inazingatia ambapo ray kupitia katikati ya lens huvuka ndege ya msingi.

Kielelezo\(\PageIndex{7}\): Mionzi ya oblique inayofanana inazingatia hatua katika ndege ya msingi.

Nyembamba-Lens Equation

Ufuatiliaji wa Ray unatuwezesha kupata picha ya ubora wa malezi ya picha. Ili kupata habari za nambari, tunapata jozi ya equations kutoka uchambuzi wa kijiometri wa kufuatilia ray kwa lenses nyembamba. Ulinganyo huu, unaoitwa equation nyembamba-lens na equation ya lens maker, kuruhusu sisi quantitatively kuchambua lenses nyembamba.

Fikiria nene bi-convex Lens inavyoonekana katika Kielelezo \(\PageIndex{8}\). Ripoti ya kukataa kati ya jirani ni n ₁ (ikiwa lens iko katika hewa, basi\(n_1=1.00\)) na ile ya lens ni\(n_2\). Radi ya curvatures ya pande mbili ni\(R_1\) na\(R_2\). Tunataka kupata uhusiano kati ya umbali wa kitu\(d_o\), umbali wa picha\(d_i\), na vigezo vya lens.

Kielelezo\(\PageIndex{8}\) kwa ajili ya deriving equation lens maker ya. Hapa,\(t\) ni unene wa lens, n ₁ ni index ya kukataa kati ya nje, na\(n_2\) ni index ya kukataa kwa lens. Tunachukua kikomo cha\(t→0\) kupata formula kwa lens nyembamba.

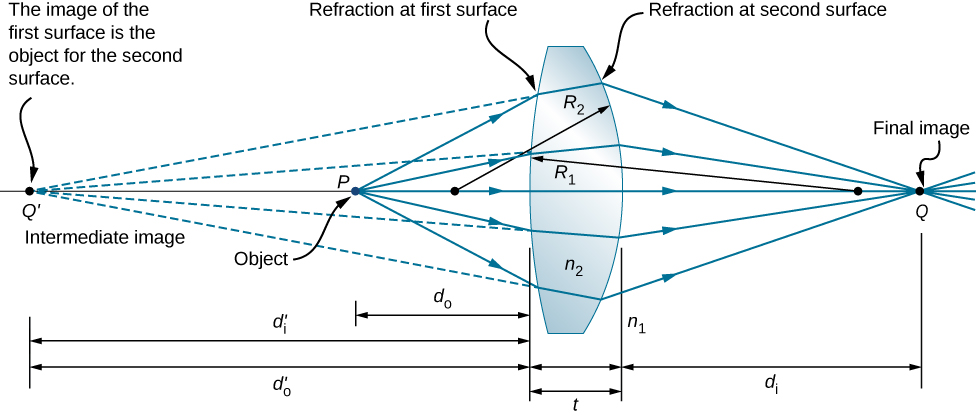
Ili kupata equation nyembamba-lens, tunazingatia picha iliyoundwa na uso wa kwanza wa kukataa (yaani, uso wa kushoto) na kisha kutumia picha hii kama kitu cha uso wa pili wa kukataa. Katika takwimu, picha kutoka kwa uso wa kwanza wa kukataa ni\(Q′\), ambayo hutengenezwa kwa kupanua nyuma mionzi kutoka ndani ya lens (mionzi haya yanatokana na kukataa kwenye uso wa kwanza). Hii inaonyeshwa na mistari iliyopigwa katika takwimu. Kumbuka kwamba picha hii ni virtual kwa sababu hakuna rays kweli kupita katika hatua Q. Ili kupata umbali wa picha\(d′_i\) unaofanana na picha Q, tunatumia Equation 2.4.9. Katika kesi hiyo, umbali wa kitu ni\(d_o\), umbali wa picha ni d'idi′, na radius ya curvature ni\(R_1\). Kuingiza hizi katika uhusiano inayotokana uliopita kwa refraction katika curves nyuso anatoa

\ [dfrac {n_1} {d_o} +\ dfrac {n_2} {d'_i} =\ dfrac {n_2,1n_1} {R_1}. \ studio {51}\]

Picha ni virtual na upande sawa na kitu, hivyo d _i <0 na d _o >0. Uso wa kwanza unakabiliwa na kitu, hivyo\(R_1>0\).

Ili kupata umbali wa kitu kwa kitu\(Q\) kilichoundwa na kukataa kutoka kwenye interface ya pili, kumbuka kuwa jukumu la fahirisi za kukataa n ₁ na n ₂ zinaingiliana katika Equation 2.4.9. Katika Kielelezo\(\PageIndex{8}\), mionzi hutoka katikati na index\(n_2\), wakati katika Mchoro 2.4.3, mionzi hutoka katikati na index \(n_1\). Hivyo, ni lazima kubadilishana n ₁ na n ₂ katika Equation 2.4.9. Aidha, kwa kushauriana tena Kielelezo\(\PageIndex{8}\), tunaona kwamba kitu umbali ni\(d′_o\) na umbali wa picha ni \(d_i\). Radi ya curvature ni R ₂ Kuingiza kiasi hiki katika Equation 2.4.9 inatoa

\ [dfrac {n_2} {d'_o} +\ dfrac {n_1} {d_i} =\ dfrac {n_1,1-n_2} {R_2}. \ studio {eq51}\]

Picha ni halisi na upande wa pili kutoka kwa kitu, hivyo \(d_i>0\) na\(d_o′>0\). Sehemu ya pili ni convex mbali na kitu, hivyo\(R_2<0\). Equation\ ref {eq51} inaweza kuwa rahisi kwa kubainisha kuwa

\[d′_o=|d′_i|+t, \nonumber \]

ambapo tumechukua thamani kamili kwa sababu\(d′_i\) ni idadi hasi, ambapo wote wawili\(d′_o\) na\(t\) ni chanya. Tunaweza kugawa na thamani kamili kama sisi yanatofautiana\(d′_i\), ambayo inatoa

\[ d′_o=−d′_i+td. \nonumber \]

Kuingiza hii katika Equation\ ref {eq51} inatoa

\ [dfrac {n_2} {-d'_i+t} +\ dfrac {n_1} {d_i} =\ dfrac {n_1,1-n_2} {R_2}. \ studio {eq52}\]

Summing equations\ ref {eq51} na\ ref {eq52} anatoa

\ [{dfrac {n_1} {d_o} +\ dfrac {n_1} {d_i} +\ dfrac {n_2} {d'_i} +\ dfrac {n_2} {-d'_i+t} = (n_2—n_1) \ kushoto (\ dfrac {1} R_1}} frac {1} {R_2}\ haki). \ studio {eq54}\]

Katika makadirio nyembamba-lens, tunadhani kwamba lens ni nyembamba sana ikilinganishwa na umbali wa kwanza wa picha, au\(t \ll d′_i\) (au , sawa,\(t \ll R_1\) na\(t \ll R_2\)). Katika kesi hii, maneno ya tatu na ya nne upande wa kushoto wa Equation\ ref {eq54} kufuta, na kuacha sisi na

\ [dfrac {n_1} {d_o} +\ dfrac {n_1} {d_i} = (n_2,1n_1)\ kushoto (\ dfrac {1} {R_1}}}} \ dfrac {1} {1} {R_1} {1} {R_1} {1} {R_1} {1} {R_1} {1} {R_1} {1} {1} {R_1} {1} { \ nambari isiyo\]

Kugawanyika na\(n_1\) inatupa hatimaye

\ [dfrac {1} {d_o} +\ dfrac {1} {d_i} =\ kushoto (\ dfrac {n_2} {n_1} -1 \ kulia)\ kushoto (\ dfrac {1} {R_1}} {R_1} {1} {R_2}\ kulia). \ studio {eq58}\]

Upande wa kushoto unaonekana kwa uangalifu kama usawa wa kioo ambao tumepata hapo juu kwa vioo vya spherical. Kama ilivyofanyika kwa vioo vya spherical, tunaweza kutumia kufuatilia ray na jiometri ili kuonyesha kwamba, kwa lens nyembamba,

\ [ \ underbrace {\ dfrac {1} {d_o} +\ dfrac {1} {d_i} =\ dfrac {1} {f}} _ { \ maandishi {nyembamba-lens equation}}\ studio {thin-lens equation}\]

\(f\)wapi urefu wa lens nyembamba ( derivation hii imesalia kama zoezi). Hii ni equation nyembamba-lens. Urefu wa urefu wa lens nyembamba ni sawa na kushoto na kulia ya lens. Kuchanganya equations \ ref {thin-lens equation} na\ ref {eq58} anatoa

\ [\ underbrace {\ dfrac {1} {f} =\ kushoto (\ dfrac {n_2} {n_1} -1\ haki)\ kushoto ( \ dfrac {1} {R_1}}}}\ dfrac {1} {R_2}\ haki)} {\ Nakala { equation maker ya lens}}\ studio {lensmaker}\]

ambayo inaitwa equation lens maker ya. Inaonyesha kwamba urefu wa msingi wa lens nyembamba hutegemea tu radii ya curvature na index ya kukataa kwa lens na ile ya kati ya jirani. Kwa lens katika hewa,\(n_1=1.0\) na\(n_2≡n\), hivyo equation lens maker inapunguza kwa

\ [dfrac {1} {f} = (n -1) \ kushoto (\ dfrac {1} {R_1}}}\ dfrac {1} {R_2}\ kulia). \ nambari isiyo\]

Saini mikataba kwa lenses

Ili kutumia vizuri equation nyembamba-lens, makusanyiko ya ishara yafuatayo yanapaswa kutii:

• \(d_i\)ni chanya ikiwa picha iko upande wa kinyume na kitu (yaani, picha halisi); vinginevyo,\(d_i\) ni hasi (yaani, picha halisi).
• \(f\)ni chanya kwa lens converging na hasi kwa lens diverging.
• \(R\)ni chanya kwa uso mbonyeo kuelekea kitu, na hasi kwa s uso concave kuelekea kitu.

Ukuaji

Kwa kutumia kitu cha ukubwa wa mwisho kwenye mhimili wa macho na kufuatilia ray, unaweza kuonyesha kwamba ukuzaji\(m\) wa picha ni

\[m \equiv \dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o} \label{mag} \]

(ambapo mistari mitatu inamaanisha “inaelezwa kama”). Hii ni sawa sawa na sisi kupatikana kwa vioo (angalia Equation 2.3.15). Ikiwa\(m>0\), basi picha ina mwelekeo sawa wa wima kama kitu (kinachoitwa picha “sawa”). Ikiwa m<0, basi picha ina mwelekeo wa wima kinyume kama kitu (kinachoitwa picha “inverted”).

Kutumia Equation Nyembamba-Lens

Ulinganisho wa lenzi nyembamba-lens na equation ya mtengenezaji wa lens hutumika kwa hali zinazohusisha lenses nyembamba. Tunachunguza vipengele vingi vya malezi ya picha katika mifano ifuatayo.

Fikiria lens nyembamba inayobadilika. Je, fomu ya picha ni wapi na aina gani ya picha inayoundwa kama kitu kinakaribia lens kutoka kwa infinity? Hii inaweza kuonekana kwa kutumia equation nyembamba-lens kwa urefu uliopewa focal ili kupanga njama umbali wa picha kama kazi ya umbali wa kitu. Kwa maneno mengine, sisi njama

\[d_i=\left(\dfrac{1}{f}−\dfrac{1}{d_o}\right)^{−1} \nonumber \]

kwa thamani fulani ya\(f\). Kwa\(f=1\,cm\), matokeo ni inavyoonekana katika Kielelezo\(\PageIndex{9a}\).

Kielelezo\(\PageIndex{9}\): (a) Umbali wa picha kwa lens nyembamba inayobadilika na f=1.0 cm kama kazi ya umbali wa kitu. (b) Kitu kimoja lakini kwa lenzi iliyogawanyika yenye f=-1.0 cm.

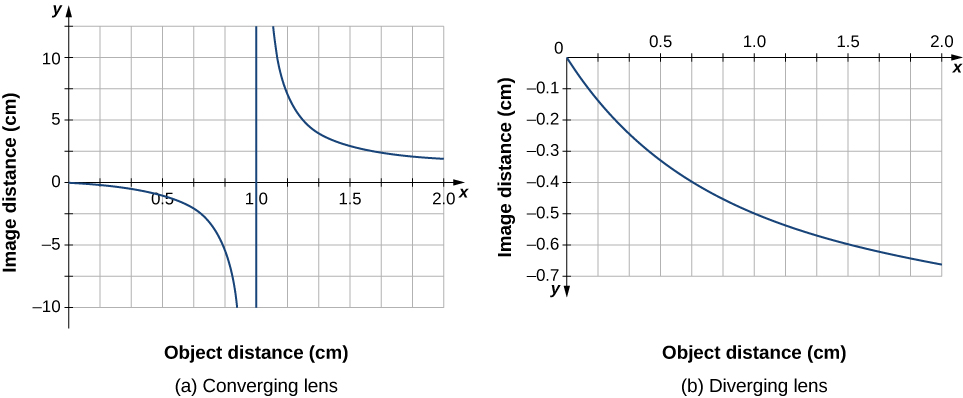
kitu mbali zaidi kuliko focal urefu f kutoka Lens lazima kuzalisha picha karibu ndege focal, kwa sababu muda wa pili upande wa kulia wa equation juu inakuwa kidogo ikilinganishwa na muda wa kwanza, hivyo tuna\(d_i≈f\). Hii inaweza kuonekana katika njama ya sehemu (a) ya takwimu, ambayo inaonyesha kwamba umbali wa picha unakaribia urefu wa urefu wa 1 cm kwa umbali mkubwa wa kitu. Kama kitu kinakaribia ndege ya msingi, umbali wa picha unajitokeza kwa infinity nzuri. Hii inatarajiwa kwa sababu kitu katika ndege ya msingi hutoa mionzi inayofanana ambayo huunda picha kwa infinity (yaani, mbali sana na lens). Wakati kitu ni mbali zaidi kuliko urefu focal kutoka lens, umbali wa picha ni chanya, hivyo picha ni halisi, upande wa pili wa lenzi kutoka kitu, na inverted (kwa sababu \(m=−d_i/d_o\) kupitia Equation\ ref {mag}). Wakati kitu ni karibu zaidi kuliko urefu focal kutoka lens, umbali wa picha inakuwa hasi, ambayo ina maana kwamba picha ni virtual, upande huo wa lens kama kitu, na wima.

Kwa lens nyembamba ya kupanua ya urefu wa focal\(f =−1.0\, cm\), njama sawa ya umbali wa picha vs umbali wa kitu inavyoonekana kwenye Mchoro\(\PageIndex{10b}\). Katika kesi hii, umbali wa picha ni hasi kwa umbali wote wa kitu chanya, ambayo ina maana kwamba picha ni ya kawaida, upande mmoja wa lens kama kitu, na sawa. Tabia hizi zinaweza pia kuonekana kwa michoro za kufuatilia ray (Kielelezo\(\PageIndex{10}\)).

Kielelezo\(\PageIndex{10}\): Dots nyekundu zinaonyesha pointi za msingi za lenses. (a) picha halisi, inverted sumu kutoka kitu ambayo ni mbali zaidi kuliko urefu focal kutoka lens converging. (b) Picha ya kawaida, iliyo sawa inayotokana na kitu kilicho karibu zaidi kuliko urefu wa msingi kutoka kwa lens. (c) virtual, picha wima sumu kutoka kitu kwamba ni mbali zaidi kuliko urefu focal kutoka lens diverging.

Kuona mfano halisi wa picha zenye wima na zilizoingizwa, angalia Kielelezo\(\PageIndex{11}\), ambacho kinaonyesha picha zilizoundwa na lenses zinazobadilika wakati kitu (uso wa mtu katika kesi hii) kinawekwa kwa umbali tofauti kutoka kwa lens. Katika sehemu (a) ya takwimu, uso wa mtu ni mbali zaidi ya urefu mmoja kutoka kwa lens, hivyo picha inverted. Kwa sehemu (b), uso wa mtu ni karibu zaidi ya urefu mmoja kutoka kwa lens, hivyo picha ni sawa.

Kielelezo\(\PageIndex{11}\): (a) Wakati lens inayobadilika inafanyika mbali zaidi ya urefu mmoja kutoka kwa uso wa mtu, picha iliyoingizwa inaundwa. Kumbuka kuwa picha iko katika mtazamo lakini uso sio, kwa sababu picha iko karibu sana na kamera inayochukua picha hii kuliko uso. (b) Picha ya haki ya uso wa mtu huzalishwa wakati lens inayobadilika inafanyika chini ya urefu mmoja kutoka kwa uso wake. (mikopo a: mabadiliko ya kazi na “DaMongman” /Flickr; mikopo b: mabadiliko ya kazi na Casey Fleser)

Kazi kupitia mifano ifuatayo ili uelewe vizuri jinsi lenses nyembamba zinavyofanya kazi.

MKAKATI WA KUTATUA MATATIZO: LENZI

• Hatua ya 1. Kuamua kama ray kufuatilia, nyembamba-lens equation, au wote itakuwa muhimu. Hata kama kufuatilia ray haitumiwi, mchoro wa makini daima ni muhimu sana. Andika alama na maadili kwenye mchoro.
• Hatua ya 2. Tambua kile kinachohitajika kuamua katika tatizo (kutambua haijulikani).
• Hatua ya 3. Fanya orodha ya kile kinachopewa au kinaweza kuhitimishwa kutokana na tatizo (kutambua ujuzi).
• Hatua ya 4. Ikiwa ufuatiliaji wa ray unahitajika, tumia sheria za kufuatilia ray zilizoorodheshwa karibu na mwanzo wa sehemu hii.
• Hatua ya 5. Matatizo mengi ya upimaji yanahitaji matumizi ya equation nyembamba-lens na/au equation ya maker lens. Tatua haya kwa wasiojulikana na uingize kiasi kilichopewa au utumie wote pamoja ili kupata haijulikani mbili.
• Hatua ya 7. Angalia ili uone kama jibu ni la busara. Je! Ishara ni sahihi? Je, mchoro au kufuatilia ray ni sawa na hesabu?

Mfano\(\PageIndex{1}\): Kutumia Equation ya Muumba wa Lens

Kupata Radius ya curvature ya lens biconcave symmetrically ardhi kutoka kioo na index ya refractive 1.55 ili urefu wake focal katika hewa ni 20 cm (kwa lens biconcave, nyuso zote mbili zina radius sawa ya curvature).

Mkakati

Tumia fomu nyembamba-lens ya equation ya lens maker:

\ [dfrac {1} {f} =\ kushoto (\ dfrac {n_2} {n_1} -1\ kulia)\ kushoto (\ dfrac {1} {R_1}}}}\ dfrac {1} {R_2}\ haki) \ nonumber\]

wapi\(R_1<0\) na\(R_2>0\). Kwa kuwa sisi ni kufanya lens linganifu biconcave, tuna\(|R_1|=|R_2|\).

Suluhisho

Tunaweza kuamua radius\(R\) ya curvature kutoka

\ [\ dfrac {1} {f} = \ kushoto (\ dfrac {n_2} {n_1} -1\ kulia)\ kushoto (\ dfrac {ї2} {R}\ kulia). \ nambari isiyo\]

Kutatua\(R\) na kuingiza\(f=−20\,cm\),\(n_2=1.55\), na \(n_1=1.00\) inatoa

\ [kuanza {align} R &=-2f\ kushoto (\ dfrac {n_2} {n_1} -1\ haki) \ nonumber\\ [4pt] &=-2 (-20\, cm) \ kushoto (\ dfrac {1.55} {1.00} -1\ haki)\ nonumber\\ [4pt] &= 22\, cm. \ nonumber\ mwisho {align}\ nonumber\]

Mfano\(\PageIndex{2}\): Kubadilisha Lens na Umbali wa Kitu tofauti

Pata eneo, mwelekeo, na ukuzaji wa picha kwa kitu cha juu cha sentimita 3.0 kwenye kila nafasi zifuatazo mbele ya lens ya mbonyeo ya urefu wa urefu wa 10.0 cm. (a) \(d_o=50.0\,cm\), (b)\(d_o=5.00\,cm\), na (c)\ (d_o=20.0\, cm\).

Mkakati

Tunaanza na equation nyembamba-lens (Equation\ ref { equation thin-lens})

\[\dfrac{1}{d_i}+\dfrac{1}{d_o}=\dfrac{1}{f}. \nonumber \]

Tatua hili kwa umbali wa picha\(d_i\) na uingize umbali wa kitu kilichopewa na urefu wa msingi.

Suluhisho

a. kwa\(d_o=50\, cm\) na\(f=+10\, cm\), hii inatoa

\ [kuanza {align} d_i &= \ kushoto (\ dfrac {1} {f} -\ dfrac {1} {d_o}\ haki) ^ {-1}\ nonumber\\ [4pt] &=\ kushoto (\ dfrac {1} {10.0\, cm} \dfrac {1} {50.0cm}\ haki) ^ {1}\ hakuna nambari \\ [4pt] &=12.5\, cm\ hakuna nambari\ mwisho {align} \ hakuna nambari\]

Picha ni chanya, hivyo picha, ni halisi, iko upande wa pili wa lens kutoka kwa kitu, na ni 12.6 cm kutoka lens. Ili kupata ukuzaji na mwelekeo wa picha, tumia

\ [kuanza {align} m &=≈\ dfrac {d_i} {d_o}\ namba\\ [4pt] &=\ dfrac {12.5\, cm} {50.0\, cm}\ hakuna namba\\ [4pt] &=-0.250. \ nonumber\ mwisho {align}\ nonumber\]

Ukuaji hasi unamaanisha kuwa picha imeingizwa. Tangu\(|m|<1\), picha ni ndogo kuliko kitu. Ukubwa wa picha hutolewa na

\ [kuanza {align} |h_i | &=|m|h_o \ nonumber\\ [4pt] & =( 0.250) (3.0\, cm)\ nonumber\\ [4pt] &=0.75\, cm\ nonumber\ mwisho {align}\ nonumber\]

b Kwa\(d_o=5.00\,cm\) na\(f=+10.0\,cm\)

\ [kuanza {align} d_i&=\ kushoto (\ dfrac {1} {f} -\ dfrac {1} {d_o}\ haki) ^ {-1}\ nonumber \\ [4pt] &=\ kushoto (\ dfrac {1} {10.0\, cm}}}\ dfrac {1} {5.00\, cm}\ kulia) ^ {-1}\ hakuna nambari\\ [4pt] &=-10.0\, cm\ namba \ mwisho {align}\ hakuna idadi\]

Umbali wa picha ni hasi, hivyo picha ni ya kawaida, iko upande mmoja wa lens kama kitu, na ni cm 10 kutoka kwa lens. Ukuaji na mwelekeo wa picha hupatikana kutoka

\ [kuanza {align} m &=\ dfrac {d_i} {d_o}\ namba\\ [4pt] &=\ dfrac {-10.0\, cm} {5.00\, cm}\ nonumber\\ [4pt] &=+2.00. \ nonumber\ mwisho {align}\ nonumber\]

Ukuaji mzuri una maana kwamba picha ni sawa (yaani, ina mwelekeo sawa na kitu). Tangu \(|m|>0\), picha ni kubwa kuliko kitu. Ukubwa wa picha ni

\ [kuanza {align} |h_i|&=|m|h_o\ nonumber\\ [4pt] & =( 2.00) (3.0\, cm)\ nonumber\\ [4pt] &=6.0\, sentimita. \ nonumber \ mwisho {align}\ nonumber\]

c Kwa\(d_o=20\,cm\) na\(f=+10cm\)

\ [kuanza {align} d_i &= \ kushoto (\ dfrac {1} {f}} -\ dfrac {1} {d_o}\ haki) ^ {-1}\ nonumber\\ [4pt] &=\ kushoto (\ dfrac {1} {10.0\, cm} {10.0\, cm}\ kulia) ^ {10.0\, cm}\ -1}\ hakuna nambari \\ [4pt] &=20.0\, cm\ hakuna nambari\ mwisho {align} \ hakuna nambari\]

Umbali wa picha ni chanya, hivyo picha ni halisi, iko upande wa pili wa lens kutoka kwa kitu, na ni 20.0 cm kutoka lens. Ukuaji ni

\ [kuanza {align} m &=≈\ dfrac {d_i} {d_o}\ namba\\ [4pt] &=-dfrac {20.0\, cm} {20.0\, cm}\ hakuna namba\\ [4pt] &=-1.00. \ nonumber\ mwisho {align}\ nonumber\]

Ukuaji hasi unamaanisha kuwa picha imeingizwa. Tangu\(|m|=1\), picha ni ukubwa sawa na kitu.

Wakati wa kutatua matatizo katika optics ya kijiometri, mara nyingi tunahitaji kuchanganya kufuatilia ray na equations lens. Mfano unaofuata unaonyesha njia hii.

Mfano\(\PageIndex{3}\): Uchaguzi wa Urefu na Aina ya Lens

Ili mradi picha ya wigo wa taa kwenye skrini 1.50 m mbali, unahitaji kuchagua aina gani ya lens ya kutumia (kugeuka au kugeuka) na urefu wake wa msingi (Kielelezo\(\PageIndex{12}\)). Umbali kati ya lens na bulb ya taa ni fasta saa 0.75 m Pia, ni nini ukuzaji na mwelekeo wa picha?

Kielelezo\(\PageIndex{12}\): Bonde la taa lililowekwa 0.75 m kutoka kwa lens yenye urefu wa 0.50-m hutoa picha halisi kwenye skrini, kama ilivyojadiliwa katika mfano. Ray kufuatilia anatabiri eneo picha na ukubwa.

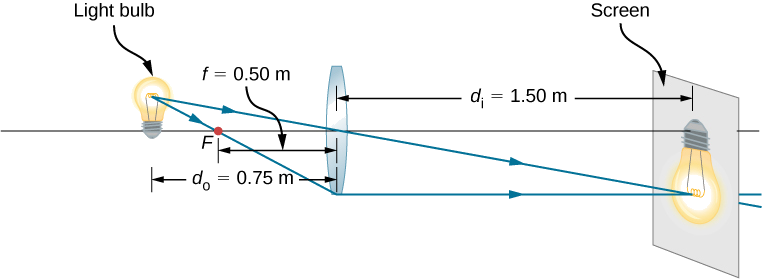
Mkakati

Picha lazima iwe halisi, kwa hiyo unachagua kutumia lens inayobadilika. Urefu wa urefu unaweza kupatikana kwa kutumia equation nyembamba-lens na kutatua kwa urefu wa focal. Umbali wa kitu ni \(d_o=0.75\,m\) na umbali wa picha ni\(d_i=1.5\,m\).

Suluhisho

Tatua lens nyembamba kwa urefu wa msingi na uingize kitu kilichohitajika na umbali wa picha:

\ [kuanza {align} \ dfrac {1} {d_o} +\ dfrac {1} {d_i} &=\ dfrac {1} {f}\ nonumber\\ [4pt] f &=\ kushoto (\ dfrac {1} {d_o} +\ dfrac {1} {1} {d_i}\ haki) ^ {-1}\ nonon nambari \\ [4pt] &= \ kushoto (\ dfrac {1} {0.75\, m} +\ dfrac {1} {1.5\, m}\ haki) ^ {-1}\ nonumber \\[4pt] &= 0.50 \, m \nonumber \end{align} \nonumber \]

Ukuaji ni

\ [kuanza {align} m &=≈\ dfrac {d_i} {d_o}\ nonumber\\ [4pt] &= -\ dfrac {1.5\, m} {0.75\, m}\ nonumber\\ [4pt] &=-2.0. \ nonumber \ mwisho {align}\ nonumber\]

Umuhimu

Ishara ndogo ya ukuzaji ina maana kwamba picha imeingizwa. Urefu wa urefu ni chanya, kama inavyotarajiwa kwa lens inayobadilika. Ufuatiliaji wa Ray unaweza kutumika kuangalia hesabu (Kielelezo\(\PageIndex{12}\)). Kama inavyotarajiwa, picha inverted, ni halisi, na ni kubwa kuliko kitu.