2.3: Vioo vya mviringo

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza malezi ya picha na vioo vya spherical.
• Tumia michoro ya ray na equation ya kioo ili kuhesabu mali ya picha katika kioo cha spherical.

Picha katika kioo cha ndege ina ukubwa sawa na kitu, ni sawa, na ni umbali sawa nyuma ya kioo kama kitu kilicho mbele ya kioo. Kioo kilichopigwa, kwa upande mwingine, kinaweza kuunda picha ambazo zinaweza kuwa kubwa au ndogo kuliko kitu na zinaweza kuunda ama mbele ya kioo au nyuma yake. Kwa ujumla, uso wowote wa mviringo utaunda picha, ingawa baadhi ya picha zinafanya kuwa hivyo kupotosha kuwa haijulikani (fikiria vioo vya nyumba za kujifurahisha). Kwa sababu vioo vyenye rangi vinaweza kuunda aina nyingi za picha, hutumiwa katika vifaa vingi vya macho ambavyo hupata matumizi mengi. Tutazingatia vioo vya spherical kwa sehemu kubwa, kwa sababu ni rahisi kutengeneza kuliko vioo kama vile vioo vya parabolic na hivyo ni kawaida zaidi.

Curved vioo

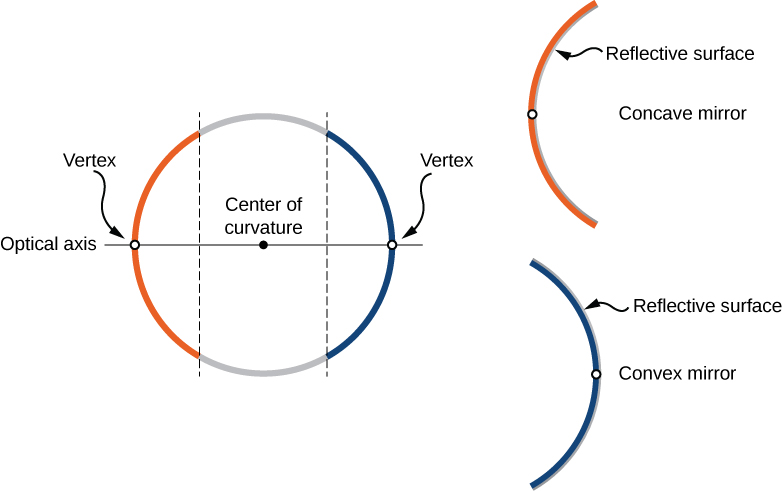
Tunaweza kufafanua aina mbili za vioo vya spherical. Ikiwa uso wa kutafakari ni upande wa nje wa nyanja, kioo kinaitwa kioo cha convex. Ikiwa uso wa ndani ni uso wa kutafakari, huitwa kioo cha concave.

Ulinganifu ni mojawapo ya alama kuu za vifaa vingi vya macho, ikiwa ni pamoja na vioo na lenses. Mhimili wa ulinganifu wa vipengele vile vya macho mara nyingi huitwa mhimili mkuu au mhimili wa macho. Kwa kioo cha spherical, mhimili wa macho hupita katikati ya kioo cha curvature na vertex ya kioo, kama inavyoonekana kwenye Mchoro\(\PageIndex{1}\).

Kielelezo\(\PageIndex{1}\). Kioo cha spherical kinaundwa kwa kukata kipande cha nyanja na kutafakari ama ndani au nje ya uso. Kioo cha concave kina fedha juu ya uso wa mambo ya ndani (fikiria “pango”), na kioo cha convex kina fedha juu ya uso wa nje.

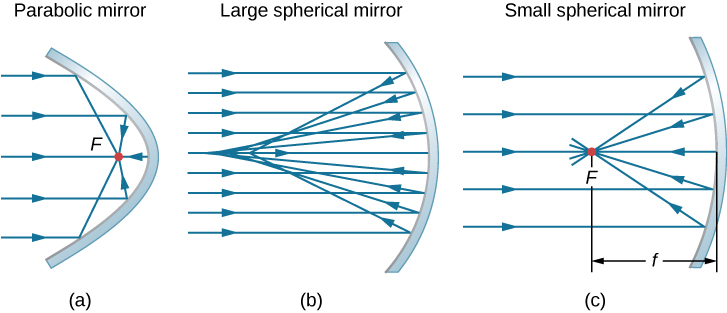
Fikiria rays kwamba ni sambamba na mhimili macho ya kioo parabolic, kama inavyoonekana katika Kielelezo\(\PageIndex{2a}\). Kufuatia sheria ya kutafakari, mionzi hii inaonekana ili waweze kugeuka kwa hatua, inayoitwa hatua ya msingi. Kielelezo\(\PageIndex{2b}\) kinaonyesha kioo cha spherical ambacho ni kikubwa ikilinganishwa na radius yake ya curvature. Kwa kioo hiki, mionzi iliyojitokeza haipatikani kwa hatua moja, hivyo kioo hakina kipaumbele kilichoelezwa vizuri. Hii inaitwa uharibifu wa spherical na matokeo katika picha iliyosababishwa ya kitu kilichopanuliwa. Kielelezo\(\PageIndex{2c}\) kinaonyesha kioo cha spherical ambacho ni chache ikilinganishwa na radius yake ya curvature. Kioo hiki ni makadirio mazuri ya kioo cha parabolic, hivyo mionzi inayofika sambamba na mhimili wa macho inaonekana kwa hatua inayofafanuliwa vizuri. Umbali pamoja na mhimili wa macho kutoka kioo hadi kwenye kituo kinachojulikana kama urefu wa kioo.

Kielelezo\(\PageIndex{2}\): (a) Mionzi sambamba yalijitokeza kutoka kioo kioo msalaba katika hatua moja inayoitwa focal F. (b) Mionzi sambamba yalijitokeza kutoka kioo kikubwa cha mviringo haipatikani kwa hatua ya kawaida. (c) Kama kioo spherical ni ndogo ikilinganishwa na radius yake ya curvature, ni bora takriban sehemu ya kati ya kioo parabolic, hivyo rays sambamba kimsingi msalaba katika hatua ya kawaida. Umbali pamoja na mhimili wa macho kutoka kioo hadi kwenye kituo cha msingi ni urefu wa kioo cha kioo.

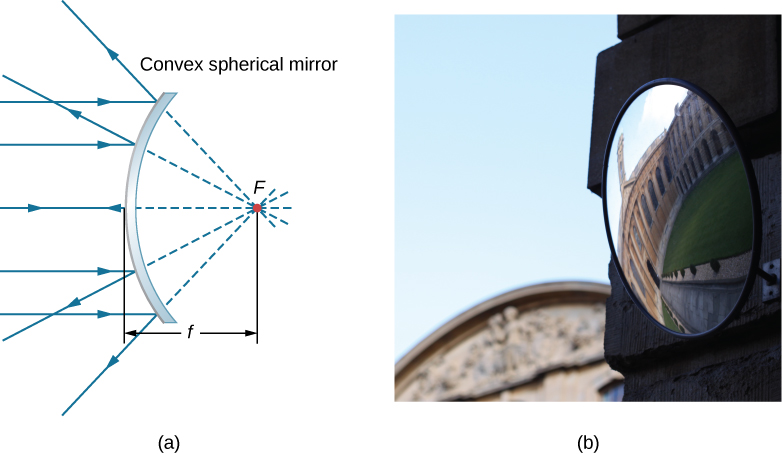
Kioo cha mviringo cha mviringo pia kina kipaumbele, kama inavyoonekana kwenye Kielelezo\(\PageIndex{3}\). Mionzi ya tukio sambamba na mhimili wa macho hujitokeza kutoka kioo na inaonekana kuwa inatoka kwenye\(F\) hatua ya urefu wa kioo\(f\) nyuma ya kioo. Hivyo, hatua kuu ni virtual kwa sababu hakuna rays halisi kweli kupita kwa njia hiyo; wao tu kuonekana asili kutoka humo.

Kielelezo\(\PageIndex{3}\): (a) Rays yalijitokeza na kioo mbonyeo spherical: Tukio mionzi ya mwanga sambamba na mhimili macho ni yalijitokeza kutoka mbonyeo kioo spherical na inaonekana kuwa asili ya focal uhakika katika focal umbali f upande wa pili wa kioo. Kitu cha msingi ni virtual kwa sababu hakuna mionzi halisi inayopita. (b) Picha ya picha halisi iliyoundwa na kioo cha mbonyeo. (mikopo b: mabadiliko ya kazi na Jenny Downing)

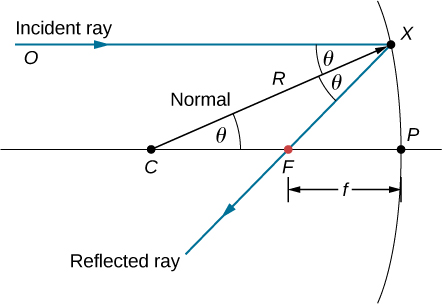
Urefu wa kioo unahusianaje na radius ya kioo ya curvature? Kielelezo\(\PageIndex{4}\) kinaonyesha ray moja ambayo inaonekana na kioo cha concave cha spherical. Ray ya tukio ni sawa na mhimili wa macho. Hatua ambayo ray iliyojitokeza inavuka mhimili wa macho ni hatua kuu. Kumbuka kwamba mionzi yote ya tukio ambayo ni sambamba na mhimili wa macho hujitokeza kupitia kituo-tunaonyesha ray moja tu kwa unyenyekevu. Tunataka kupata jinsi urefu wa msingi\(FP\) (uliotajwa na\(f\)) unahusiana na radius ya curvature ya kioo\(R\), ambaye urefu wake ni

\[R=CF+FP. \label{eq31} \]

Sheria ya kutafakari inatuambia kuwa pembe\(\angle OXC\) na\(\angle CXF\) ni sawa, na kwa sababu ray ya tukio ni sawa na mhimili wa macho, pembe\(\angle OXC\) na pia\(\angle XCP\) ni sawa. Hivyo, pembetatu\(CXF\) ni pembetatu ya isosceles na\(CF=FX\). Ikiwa angle\(θ\) ni ndogo basi

\[\sin θ≈ θ \label{sma} \]

ambayo inaitwa “ndogo-angle makadirio”), basi\(FX≈FP\) au\(CF≈FP\). Kuingiza hii katika Equation\ ref {eq31} kwa radius\(R\), tunapata

\[\begin{align} R &=CF+FP \nonumber \\[4pt] &=FP+FP \nonumber \\[4pt] &=2FP\nonumber \\[4pt] &=2f \end{align} \nonumber \]

Kwa maneno mengine, katika makadirio ya angle ndogo, urefu wa kioo\(f\) cha concave spherical ni nusu ya radius yake ya curvature,\(R\):

\[f=\dfrac{R}{2}. \nonumber \]

Katika sura hii, sisi kudhani kwamba ndogo-angle makadirio (pia hujulikana makadirio paraxial) daima halali. Katika makadirio haya, mionzi yote ni mionzi ya paraxial, ambayo ina maana kwamba hufanya angle ndogo na mhimili wa macho na iko mbali sana kuliko radius ya curvature kutoka mhimili wa macho. Katika kesi hiyo, pembe zao\(θ\) za kutafakari ni pembe ndogo, hivyo

\[\sin θ≈ \tan θ≈ θ. \label{smallangle} \]

Kielelezo\(\PageIndex{4}\): Tafakari katika kioo cha concave. Katika makadirio ya angle ndogo, ray inayofanana na CP ya mhimili wa macho inaonekana kupitia hatua ya F ya kioo.

Kutumia Ray Kufuatilia Machapisho Picha

Ili kupata eneo la picha iliyoundwa na kioo cha mviringo, sisi kwanza kutumia ray kufuatilia, ambayo ni mbinu ya kuchora rays na kutumia sheria ya kutafakari kuamua rays yalijitokeza (baadaye, kwa lenses, tunatumia sheria ya kukataa kuamua rays refracted). Pamoja na jiometri ya msingi, tunaweza kutumia kufuatilia ray ili kupata kituo cha msingi, eneo la picha, na maelezo mengine kuhusu jinsi kioo kinachotumia mwanga. Kwa kweli, tumetumia kufuatilia ray hapo juu ili kupata sehemu ya msingi ya vioo vya spherical, au umbali wa picha ya vioo vya gorofa. Ili kupata picha ya kitu, lazima upate angalau pointi mbili za picha. Kuweka kila hatua inahitaji kuchora angalau mionzi miwili kutoka kwenye hatua juu ya kitu na kujenga mionzi yao iliyojitokeza. Hatua ambayo mionzi iliyojitokeza inaingiliana, ama katika nafasi halisi au katika nafasi halisi, ni wapi hatua inayofanana ya picha iko. Ili kufanya ray kufuatilia rahisi, tunazingatia mionzi minne “kuu” ambayo tafakari ni rahisi kujenga.

Kielelezo\(\PageIndex{5}\) kinaonyesha kioo cha concave na kioo cha mchanganyiko, kila mmoja ana kitu kilicho na mshale mbele yake. Hizi ni vitu ambao picha tunataka Machapisho kwa kufuatilia ray. Kwa kufanya hivyo, tunapata mionzi kutoka kwenye hatua\(Q\) ambayo iko kwenye kitu lakini si kwenye mhimili wa macho. Sisi kuchagua kuteka ray yetu kutoka ncha ya kitu. kuu ray 1 huenda kutoka hatua\(Q\) na kusafiri sambamba na mhimili macho. Kutafakari kwa ray hii lazima kupita kupitia hatua ya msingi, kama ilivyojadiliwa hapo juu. Kwa hiyo, kwa kioo cha concave, kutafakari kwa ray kuu 1 hupitia hatua ya msingi\(F\), kama inavyoonekana kwenye Mchoro\(\PageIndex{5b}\). Kwa kioo cha convex, ugani wa nyuma wa kutafakari kwa ray kuu 1 hupitia hatua ya msingi (yaani, lengo la kawaida). Mkuu ray 2 husafiri kwanza kwenye mstari unaopitia hatua ya msingi na kisha inaonekana nyuma kwenye mstari unaofanana na mhimili wa macho. Radi kuu 3 husafiri kuelekea katikati ya kioo cha kioo, hivyo hupiga kioo kwa matukio ya kawaida na inaonekana nyuma kwenye mstari uliotoka. Hatimaye, ray kuu 4 hupiga vertex ya kioo na inaonekana kwa usawa kuhusu mhimili wa macho.

Kielelezo\(\PageIndex{5}\): mionzi minne kuu inavyoonekana kwa wote (a) kioo concave na (b) kioo convex. Picha huunda ambapo mionzi huingiliana (kwa picha halisi) au ambapo upanuzi wao wa nyuma unaingiliana (kwa picha za kawaida).

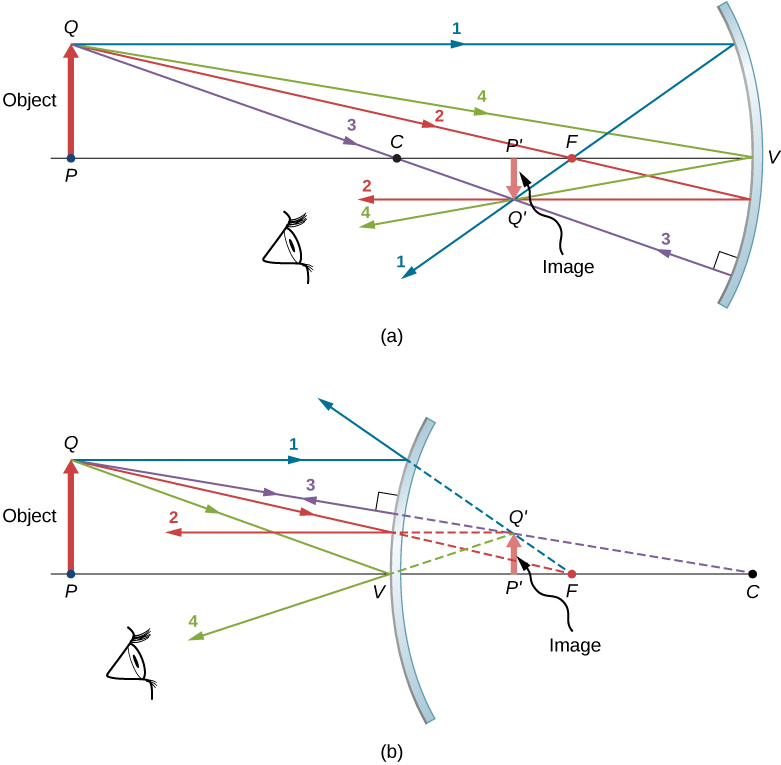
Mionzi minne kuu inaingiliana kwa hatua\(Q′\), ambayo ndio ambapo picha ya uhakika\(Q\) iko. Machapisho uhakika\(Q′\), kuchora yoyote mbili ya rays kanuni hizi ingekuwa inatosha. Sisi ni hivyo huru kuchagua yoyote ya mionzi kuu tunataka kupata picha. Kuchora zaidi ya mionzi miwili kuu wakati mwingine ni muhimu kuthibitisha kuwa kufuatilia ray ni sahihi.

Ili kupata kabisa picha iliyopanuliwa, tunahitaji kupata hatua ya pili katika picha, ili tuweze kujua jinsi picha inavyoelekezwa. Ili kufanya hivyo, tunaelezea mionzi kuu kutoka chini ya kitu. Katika kesi hiyo, mionzi yote minne kuu inaendesha kando ya mhimili wa macho, kutafakari kutoka kioo, na kisha kukimbia nyuma pamoja na mhimili wa macho. Ugumu ni kwamba, kwa sababu mionzi hii ni collinear, hatuwezi kuamua uhakika wa kipekee ambapo wao intersect. Yote tunayojua ni kwamba msingi wa picha ni kwenye mhimili wa macho. Hata hivyo, kwa sababu kioo ni sawa kutoka juu hadi chini, haibadili mwelekeo wa wima wa kitu. Hivyo, kwa sababu kitu ni wima, picha lazima iwe wima. Kwa hiyo, picha ya msingi wa kitu ni kwenye mhimili wa macho moja kwa moja juu ya picha ya ncha, kama inayotolewa kwenye takwimu.

Kwa kioo cha concave, picha iliyopanuliwa katika kesi hii inaunda kati ya hatua kuu na katikati ya curvature ya kioo. Ni inverted kwa heshima na kitu, ni picha halisi, na ni ndogo kuliko kitu. Kama sisi kusonga kitu karibu na au mbali na kioo, tabia ya picha itabadilika. Kwa mfano, tunaonyesha, kama zoezi la baadaye, kwamba kitu kilichowekwa kati ya kioo cha concave na kiini chake kinasababisha picha ya kawaida ambayo ni sawa na kubwa kuliko kitu. Kwa kioo cha convex, fomu ya picha iliyopanuliwa kati ya hatua ya msingi na kioo. Ni sawa kwa heshima na kitu, ni picha virtual, na ni ndogo kuliko kitu.

Ray-Tracking Kanuni

Kufuatilia Ray ni muhimu sana kwa vioo. Sheria za kufuatilia ray zinafupishwa hapa kwa kumbukumbu:

• Ray inayosafiri sambamba na mhimili wa macho ya kioo cha spherical inaonekana kwenye mstari unaotembea kupitia sehemu ya msingi ya kioo (ray 1 katika Kielelezo\(\PageIndex{5}\)).
• Ray inayosafiri kwenye mstari unaozunguka kupitia kiini cha kioo cha spherical inaonekana kwenye mstari unaofanana na mhimili wa macho wa kioo (ray 2 katika Mchoro\(\PageIndex{5}\)).
• Ray inayosafiri kwenye mstari unaoendelea katikati ya kioo cha kioo cha spherical inaonekana nyuma kwenye mstari huo (ray 3 katika Kielelezo\(\PageIndex{5}\)).
• Ray ambayo hupiga vertex ya kioo cha spherical inaonekana kwa usawa kuhusu mhimili wa macho wa kioo (ray 4 katika Kielelezo\(\PageIndex{5}\)).

Tunatumia kufuatilia ray kuonyesha jinsi picha zinaundwa na vioo na kupata taarifa za namba kuhusu mali ya macho ya kioo. Kama sisi kudhani kwamba kioo ni ndogo ikilinganishwa na radius yake ya curvature, tunaweza pia kutumia algebra na jiometri kupata equation kioo, ambayo sisi kufanya katika sehemu inayofuata. Kuchanganya kufuatilia ray na equation kioo ni njia nzuri ya kuchambua mifumo ya kioo.

Uundaji wa picha na kutafakari — Ulinganisho wa Kioo

Kwa kioo cha ndege, tulionyesha kuwa picha iliyoundwa ina urefu sawa na mwelekeo kama kitu, na iko umbali sawa nyuma ya kioo kama kitu kilicho mbele ya kioo. Ingawa hali ni ngumu zaidi kwa vioo vya mawe, kutumia jiometri inaongoza kwa formula rahisi zinazohusiana na umbali wa kitu na picha kwa urefu wa focal wa vioo vya concave na vyema.

Kielelezo\(\PageIndex{6}\): Picha iliyoundwa na kioo cha concave.

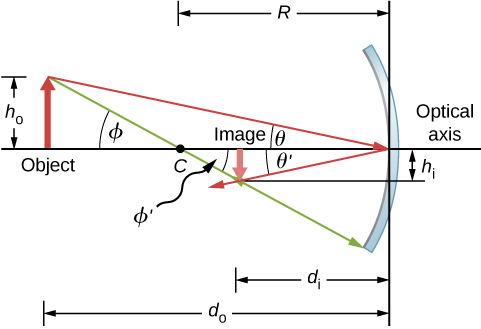
Fikiria kitu\(OP\) kilichoonyeshwa kwenye Kielelezo\(\PageIndex{6}\). Katikati ya curvature ya kioo ni lebo\(C\) na ni umbali\(R\) kutoka vertex ya kioo, kama ilivyowekwa katika takwimu. Umbali wa kitu na picha ni lebo\(d_o\) na\(d_i\), na urefu wa kitu na picha zimeandikwa\(h_o\) na\(h_i\), kwa mtiririko huo. Kwa sababu pembe\(ϕ\) na\(ϕ′\) ni pembe mbadala ya mambo ya ndani, tunajua kwamba wana ukubwa sawa. Hata hivyo, wanapaswa kutofautiana katika ishara ikiwa tunapima pembe kutoka kwa mhimili wa macho, hivyo\(ϕ=−ϕ′\). Hali sawa inashikilia pembe\(θ\) na\(θ′\). Sheria ya kutafakari inatuambia kuwa wana ukubwa sawa, lakini ishara zao zinapaswa kutofautiana ikiwa tunapima pembe kutoka kwa mhimili wa macho. Hivyo,\(θ=−θ′\). Kuchukua tangent ya pembe\(θ\) na\(θ′\), na kutumia mali ambayo\(\tan(−θ)=−\tan θ\), inatupa

\[\left. \begin{array}{rcl} \tanθ=\dfrac{h_o}{d_o} \\ \tanθ′=−\tanθ=\dfrac{h_i}{d_i} \end{array}\right\} =\dfrac{h_o}{d_o}=−\dfrac{h_i}{d_i} \label{eq51} \]

au

\[- \dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}.\label{eq52} \]

Vile vile, kuchukua tangent ya\(ϕ\) na\(ϕ′\) anatoa

\[\left. \begin{array}{rcl} \tanϕ=\dfrac{h_o}{d_o-R} \\ \tanϕ′=−\tanϕ=\dfrac{h_i}{R-d_i} \end{array}\right\} =\dfrac{h_o}{d_o-R}=−\dfrac{h_i}{R-d_i} \nonumber \]

au

\[−\dfrac{h_o}{h_i}=\dfrac{d_o-R}{R-d_i}. \label{eq55} \]

Kuchanganya Equation\ ref {eq51} na\ ref {eq55} inatoa

\[\dfrac{d_o}{d_i}=\dfrac{d_o−R}{R−d_i}. \nonumber \]

Baada ya algebra kidogo, hii inakuwa

\[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{2}{R}. \label{eq57} \]

Hakuna makadirio inahitajika kwa matokeo haya, hivyo ni halisi. Hata hivyo, kama ilivyojadiliwa hapo juu, katika makadirio ya angle ndogo, urefu wa kioo cha spherical ni nusu ya radius ya curvature ya kioo, au\(f=R/2\). Kuingiza hii katika Equation\ ref {eq57} anatoa kioo equation:

\[\underbrace{ \dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{1}{f}}_{\text{mirror equation}}. \label{mirror equation} \]

Kioo equation inahusiana picha na kitu umbali kwa umbali focal na ni halali tu katika makadirio ndogo-angle (Equation\ ref {sma}). Ingawa ilitokana na kioo cha concave, pia inashikilia vioo vya convex (kuthibitisha hii imesalia kama zoezi). Tunaweza kupanua equation kioo kwa kesi ya kioo ndege kwa kubainisha kuwa kioo ndege ina radius usio wa curvature. Hii ina maana hatua ya msingi ni katika infinity, hivyo equation kioo simplifies kwa

\[d_o=−d_i \nonumber \]

ambayo ni equation sawa kupatikana mapema.

Kumbuka kwamba tumekuwa makini sana na ishara katika deriving kioo equation. Kwa kioo cha ndege, umbali wa picha una ishara tofauti ya umbali wa kitu. Pia, picha halisi iliyoundwa na kioo cha concave katika Kielelezo\(\PageIndex{6}\) iko upande wa pili wa mhimili wa macho kwa heshima na kitu. Katika kesi hii, urefu wa picha unapaswa kuwa na ishara tofauti ya urefu wa kitu. Kuweka wimbo wa ishara za wingi mbalimbali katika equation kioo, sisi sasa kuanzisha mkataba ishara.

Ishara mkataba kwa vioo vya spherical

Kutumia mkataba wa ishara thabiti ni muhimu sana katika optics ya kijiometri. Inatoa maadili mazuri au hasi kwa kiasi ambacho kinaonyesha mfumo wa macho. Kuelewa mkataba wa ishara inakuwezesha kuelezea picha bila kujenga mchoro wa ray. Nakala hii inatumia zifuatazo ishara mkataba:

1. Urefu wa urefu\(f\) ni chanya kwa vioo vya concave na hasi kwa vioo vya convex.
2. Umbali wa picha\(d_i\) ni chanya kwa picha halisi na hasi kwa picha za kawaida.

Angalia kwamba utawala 1 ina maana kwamba radius ya curvature ya kioo spherical inaweza kuwa chanya au hasi. Ina maana gani kuwa na radius hasi ya curvature? Hii ina maana tu kwamba radius ya curvature kwa kioo convex inaelezwa kuwa hasi.

Ukuaji wa picha

Hebu kutumia mkataba ishara kwa zaidi kutafsiri derivation ya kioo equation. Katika deriving equation hii, tuligundua kwamba kitu na picha urefu ni kuhusiana na

\[−\dfrac{h_o}{h_i}=\dfrac{d_o}{d_i}. \label{eq61} \]

Angalia Ulinganisho\ ref {eq52}. Wote kitu na picha iliyoundwa na kioo katika Kielelezo\(\PageIndex{6}\) ni halisi, hivyo umbali wa kitu na picha ni chanya. Sehemu ya juu ya kitu ni juu ya mhimili wa macho, hivyo urefu wa kitu ni chanya. Picha, hata hivyo, iko chini ya mhimili wa macho, hivyo urefu wa picha ni hasi. Hivyo, mkataba huu ishara ni sambamba na derivation yetu ya kioo equation.

Equation\ ref {eq61} kwa kweli inaelezea ukuzaji wa mstari (mara nyingi huitwa tu “ukuzaji”) wa picha kwa suala la kitu na umbali wa picha. Sisi hivyo kufafanua ukuzaji dimensionless\(m\) kama ifuatavyo:

\[\underbrace{m=\dfrac{h_i}{h_o}}_{\text{linear magnification}}. \label{mag} \]

Ikiwa\(m\) ni chanya, picha ni sawa, na ikiwa\(m\) ni hasi, picha inaingizwa. Ikiwa\(|m|>1\), picha ni kubwa kuliko kitu, na ikiwa\(|m|<1\), picha ni ndogo kuliko kitu. Kwa ufafanuzi huu wa ukuzaji, tunapata uhusiano wafuatayo kati ya kitu cha wima na cha usawa na umbali wa picha:

\[m=\dfrac{h_i}{h_o}=−\dfrac{d_i}{d_o}. \nonumber \]

Hii ni uhusiano muhimu sana kwa sababu inakuwezesha kupata ukuzaji wa picha kutoka umbali wa kitu na picha, ambayo unaweza kupata kutoka kioo equation.

Mfano\(\PageIndex{1}\): Solar Electric Generating System

Mojawapo ya teknolojia za jua zinazotumiwa leo kwa kuzalisha umeme inahusisha kifaa (kinachoitwa mfereji wa parabolic au mtoza wa kuzingatia) kinachozingatia mwanga wa jua kwenye bomba lililosawijika ambalo lina maji. Maji haya yenye joto hupigwa kwa mchanganyiko wa joto, ambapo nishati ya joto huhamishiwa kwenye mfumo mwingine unaotumiwa kuzalisha mvuke na hatimaye huzalisha umeme kupitia mzunguko wa kawaida wa mvuke. Kielelezo\(\PageIndex{7}\) kinaonyesha mfumo huo wa kufanya kazi kusini mwa California. Kioo halisi ni silinda ya parabolic na lengo lake liko kwenye bomba; hata hivyo, tunaweza takriban kioo kama robo moja ya silinda ya mviringo.

Kielelezo\(\PageIndex{7}\): Parabolic kupitia nyimbo watoza ni kutumika kuzalisha umeme katika kusini mwa California. (mikopo: “kjkolb” /Wikimedia Commons)

1. Ikiwa tunataka mionzi kutoka jua kuzingatia cm 40.0 kutoka kioo, ni nini radius ya kioo?
2. Je, ni kiasi gani cha jua kilichojilimbikizia kwenye bomba, kwa mita ya urefu wa bomba, kuchukua uharibifu (tukio la mionzi ya jua) ni 900 W/m ²?
3. Ikiwa bomba la kubeba maji lina kipenyo cha 2.00-cm, ni ongezeko gani la joto la maji kwa mita ya bomba kwa muda wa dakika 1? Fikiria kwamba kila tukio la mionzi ya jua kwenye kutafakari linafyonzwa na bomba, na kwamba maji ni mafuta ya madini.

Mkakati

Kwanza kutambua kanuni za kimwili zinazohusika. Sehemu (a) inahusiana na optics ya vioo vya spherical. Sehemu (b) inahusisha hesabu kidogo, hasa jiometri. Sehemu (c) inahitaji ufahamu wa joto na wiani.

Suluhisho

a. jua ni kitu, hivyo umbali kitu kimsingi ni infinity:\(d_o=\infty\). Umbali wa picha unayotaka ni\(d_i=40.0\,cm\). Tunatumia equation ya kioo (Equation\ ref {kioo equation}) ili kupata urefu wa kioo:

\[\begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &=\dfrac{1}{f} \nonumber \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1} \\[4pt] &= \left(\dfrac{1}{\infty}+\dfrac{1}{40.0\,cm}\right)^{−1} \\[4pt] &= 40.0 \,cm \end{align*} \nonumber \]

Hivyo, radius ya kioo ni

\[R=2f=80.0\,cm. \nonumber \]

b. insolation ni 900 W/m ². Lazima kupata sehemu ya msalaba\(A\) wa kioo concave, tangu nguvu iliyotolewa ni\(900\, W/m^2×A\). Kioo katika kesi hii ni sehemu ya robo ya silinda, hivyo eneo la urefu\(L\) wa kioo ni\(A=\frac{1}{4}(2πR)L\). Eneo la urefu wa 1.00 m ni basi

\[\begin{align*} A&=\dfrac{\pi}{2}R(1.00m) \\[4pt] &=\dfrac{(3.14)}{2}(0.800\,m)(1.00\,m) \\[4pt] &=1.26\,m^2. \end{align*} \nonumber \]

Insolation juu ya urefu wa 1.00-m ya bomba ni basi

\[(9.00×10^2\dfrac{W}{m^2})(1.26\,m^2)=1130\,W. \nonumber \]

c. ongezeko la joto hutolewa na\(Q=mcΔT\). Masi\(m\) ya mafuta ya madini katika sehemu moja ya mita ya bomba ni

\[ \begin{align*} m &= ρV = ρπ\left(\dfrac{d}{2}\right)^2(1.00\,m) \nonumber \\[4pt] &=(8.00×10^2kg/m^3)(3.14)(0.0100\,m)^2(1.00\,m) \nonumber \\[4pt] &=0.251\,kg \end{align*} \nonumber \]

Kwa hiyo, ongezeko la joto kwa dakika moja ni

\[ \begin{align*} \Delta T&= \dfrac{Q}{mc} \nonumber \\[4pt] &=\dfrac{(1130\,W)(60.0\,s)}{(0.251\,kg)(1670\,J⋅kg/°C)} \nonumber \\[4pt] &=162°\end{align*} \nonumber \]

Umuhimu

Safu ya mabomba hayo katika jangwa la California yanaweza kutoa pato la joto la MW 250 siku ya jua, huku maji yakifikia joto la juu kama 400°C Tunazingatia mita moja tu ya bomba hapa na kupuuza hasara za joto kwenye bomba.

Mfano\(\PageIndex{2}\): Image in a Convex Mirror

Keratometer ni kifaa kinachotumiwa kupima curvature ya kornea ya jicho, hasa kwa lenses zinazofaa za mawasiliano. Mwanga unaonekana kutoka kwenye kamba, ambayo hufanya kama kioo cha convex, na keratometer inachukua ukubwa wa picha hiyo. Kidogo cha kukuza, ndogo ya radius ya curvature ya kamba. Ikiwa chanzo cha mwanga ni cm 12 kutoka kwenye kamba na ukuzaji wa picha ni 0.032, ni nini radius ya curvature ya kamba?

Mkakati

Ikiwa unapata urefu wa kioo cha convex kilichoundwa na kamba, basi unajua radius yake ya curvature (ni mara mbili urefu wa focal). Umbali wa kitu ni d _o =12cm na ukuzaji ni m=0.032. Kwanza kupata umbali wa picha\(d_i\) na kisha utatua kwa urefu wa msingi\(f\).

Suluhisho

Anza na equation kwa ukuzaji (Equation\ ref {mag}) na kutatua kwa\(d_i\) na kuingiza maadili yaliyotolewa mavuno

\[d_i=−m d_o=−(0.032)(12\,cm)=−0.384\,cm \nonumber \]

ambapo sisi kubakia ziada muhimu takwimu kwa sababu hii ni hatua ya kati katika hesabu. Tatua usawa wa kioo kwa urefu wa msingi\(f\) na uingize maadili inayojulikana kwa umbali wa kitu na picha. Matokeo yake ni

\[ \begin{align*} \dfrac{1}{d_o}+\dfrac{1}{d_i} &= \dfrac{1}{f} \\[4pt] f &= \left(\dfrac{1}{d_o}+\dfrac{1}{d_i}\right)^{−1}  \\[4pt] &= \left(\dfrac{1}{12cm}+\dfrac{1}{-0.384cm}\right)^{−1} \\[4pt] &=-40.0 \,cm \end{align*} \nonumber \]

Radi ya curvature ni mara mbili urefu wa msingi, hivyo

\[R=2f=−0.80\,cm \nonumber \]

Umuhimu

Urefu wa urefu ni hasi, hivyo lengo ni la kawaida, kama inavyotarajiwa kwa kioo cha concave na kitu halisi. Radi ya curvature iliyopatikana hapa ni busara kwa kamba. Umbali kutoka kwa kamba hadi retina katika jicho la watu wazima ni karibu 2.0 cm. Katika mazoezi, corneas haiwezi kuwa spherical, ambayo inahusisha kazi ya lenses zinazofaa za kuwasiliana. Kumbuka kuwa umbali wa picha hapa ni hasi, kulingana na ukweli kwamba picha iko nyuma ya kioo. Hivyo, picha ni virtual kwa sababu hakuna rays kweli kupita kwa njia hiyo. Katika matatizo na mazoezi, utaonyesha kuwa, kwa umbali wa kitu kilichowekwa, radius ndogo ya curvature inafanana na ukubwa mdogo.

MKAKATI WA KUTATUA MATATIZO: VIOO

• Hatua ya 1. Kwanza hakikisha kwamba malezi ya picha na kioo cha spherical inahusika.
• Hatua ya 2. Kuamua kama ray kufuatilia, kioo equation, au wote ni required. Mchoro ni muhimu sana hata kama ufuatiliaji wa ray hauhitajiki hasa na tatizo. Andika alama na maadili inayojulikana kwenye mchoro.
• Hatua ya 3. Tambua hasa kile kinachohitajika kuamua katika tatizo (kutambua haijulikani).
• Hatua ya 4. Fanya orodha ya kile kinachopewa au kinaweza kuhitimishwa kutokana na tatizo kama ilivyoelezwa (kutambua ujuzi).
• Hatua ya 5. Ikiwa ufuatiliaji wa ray unahitajika, tumia sheria za kufuatilia ray zilizoorodheshwa karibu na mwanzo wa sehemu hii.
• Hatua ya 6. Matatizo mengi ya kiasi yanahitaji kutumia kioo equation. Tumia mifano kama viongozi wa kutumia equation kioo.
• Hatua ya 7. Angalia ili uone kama jibu lina maana. Je! Ishara za umbali wa kitu, umbali wa picha, na urefu wa focal zinahusiana na kile kinachotarajiwa kutoka kwa kufuatilia ray? Je! Ishara ya ukuzaji ni sahihi? Je, umbali wa kitu na picha ni busara?

Kuondoka kutoka Makadirio ya Ndogo-Angle

Makadirio madogo-angle (Equation\ ref {smallangle}) ni jiwe la msingi la majadiliano hapo juu ya malezi ya picha na kioo cha spherical. Wakati makadirio haya yamevunjwa, basi picha iliyoundwa na kioo cha spherical inapotoshwa. Uharibifu huo huitwa aberration. Hapa tunazungumzia kwa ufupi aina mbili za uharibifu: upungufu wa spherical na coma.

Upotovu wa spherical

Fikiria boriti pana ya mionzi inayofanana inayoathiri kioo cha spherical, kama inavyoonekana kwenye Mchoro\(\PageIndex{8}\). Mbali na mhimili wa macho mgomo wa mionzi, mbaya zaidi kioo cha spherical kinafikia kioo cha parabolic. Kwa hiyo, mionzi hii haijalenga kwa hatua sawa na mionzi iliyo karibu na mhimili wa macho, kama inavyoonekana kwenye takwimu. Kwa sababu ya upungufu wa spherical, picha ya kitu kilichopanuliwa kwenye kioo cha spherical kitakuwa kibaya. Upungufu wa spherical ni tabia ya vioo na lenses ambazo tunazingatia katika sehemu ifuatayo ya sura hii (vioo vya kisasa zaidi na lenses zinahitajika ili kuondokana na upungufu wa spherical).

Kielelezo\(\PageIndex{8}\): (a) Kwa upungufu wa spherical, mionzi iliyo mbali zaidi na mhimili wa macho na mionzi iliyo karibu na mhimili wa macho inalenga katika pointi tofauti. Angalia kwamba uharibifu unakuwa mbaya zaidi kwa mionzi mbali na mhimili wa macho. (b) Kwa uharibifu wa comatic, mionzi sambamba ambayo si sawa na mhimili wa macho inalenga katika urefu tofauti na urefu tofauti, hivyo picha ina “mkia” kama comet (ambayo ni “coma” katika Kilatini). Kumbuka kwamba mionzi ya rangi ni tu kuwezesha kutazama; rangi hazionyeshe rangi ya nuru.

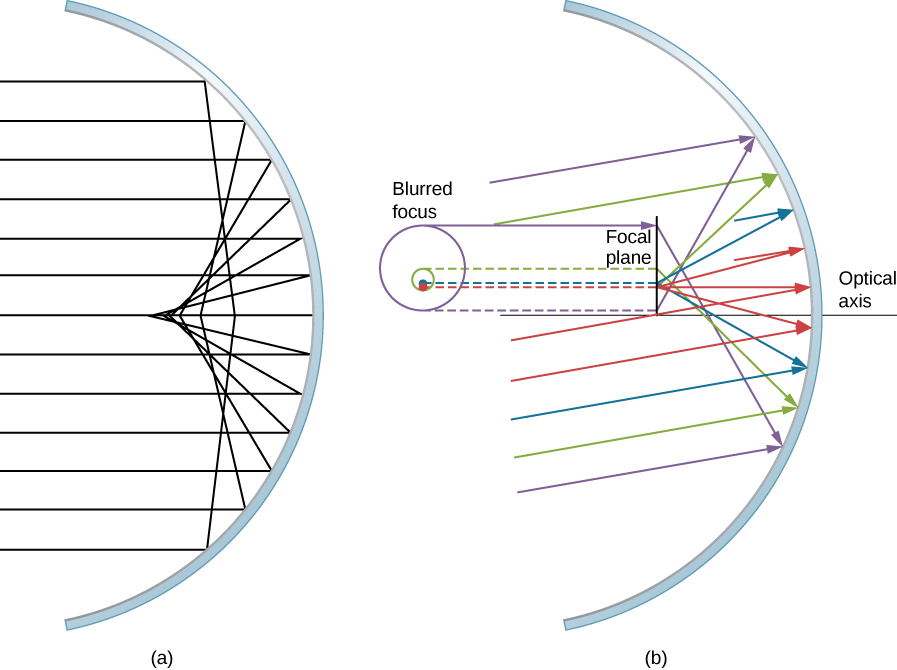
Coma au Uharibifu wa Comatic

Coma ni sawa na upungufu wa spherical, lakini hutokea wakati mionzi inayoingia haipatikani na mhimili wa macho, kama inavyoonekana kwenye Mchoro\(\PageIndex{8b}\). Kumbuka kwamba makadirio madogo ya angle inashikilia vioo vya spherical ambavyo ni ndogo ikilinganishwa na radius yao. Katika kesi hiyo, vioo vya spherical ni makadirio mazuri ya vioo vya parabolic. Vioo vya parabolic huzingatia mionzi yote ambayo ni sawa na mhimili wa macho kwenye hatua ya msingi. Hata hivyo, rays sambamba ambayo si sambamba na mhimili macho ni kulenga katika urefu tofauti na katika urefu tofauti focal, kama inavyoonekana katika Kielelezo\(\PageIndex{8b}\). Kwa sababu kioo cha spherical ni sawa na mhimili wa macho, mionzi mbalimbali ya rangi katika takwimu hii huunda miduara ya rangi inayofanana kwenye ndege ya msingi.

Ingawa kioo spherical ni inavyoonekana katika Kielelezo\(\PageIndex{8b}\), comatic aberration hutokea pia kwa vioo-parabolic haina matokeo ya kuvunjika kwa makadirio ndogo-angle (Equation\ ref {smallangle}). Upungufu wa spherical, hata hivyo, hutokea tu kwa vioo vya spherical na ni matokeo ya kuvunjika kwa makadirio madogo ya angle. Tutazungumzia coma na uharibifu wa spherical baadaye katika sura hii, kuhusiana na darubini.