1.2: Uenezi wa Mwanga

Last updated
Save as PDF

Page ID: 175419

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Kuamua index ya refraction, kutokana na kasi ya mwanga katika kati
Andika orodha ya njia ambazo mwanga husafiri kutoka chanzo hadi mahali pengine

Kasi ya Mwanga: Vipimo vya Mapema

Kipimo cha kwanza cha kasi ya nuru kilifanywa na mwanaastronomia wa Denmark Ole Roemer (1644—1710) mwaka 1675. Alisoma obiti ya Io, moja kati ya miezi minne mikubwa ya Jupiter, na kugundua kuwa ilikuwa na kipindi cha mapinduzi ya saa 42.5 karibu na Jupiter. Aligundua pia kwamba thamani hii ilibadilika kwa sekunde chache, kulingana na nafasi ya Dunia katika obiti yake karibu na Jua. Roemer alitambua kwamba kushuka kwa thamani hii ilikuwa kutokana na kasi ya mwisho ya mwanga na inaweza kutumika kuamua c.

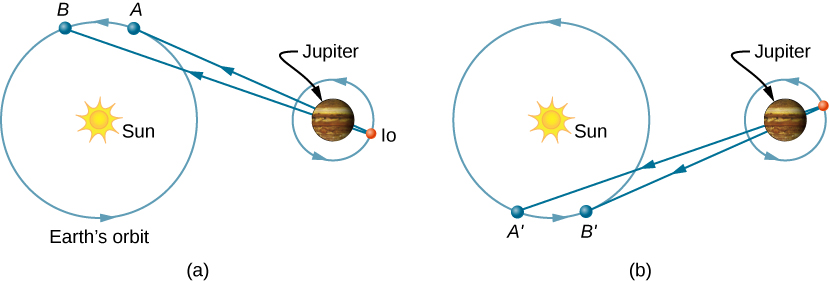
Roemer alipata kipindi cha mapinduzi ya Io kwa kupima muda wa muda kati ya eclipses mfululizo na Jupiter. Kielelezo \(\PageIndex{1a}\) kinaonyesha usanidi wa sayari wakati kipimo hicho kinafanywa kutoka Dunia katika sehemu ya obiti yake ambapo inapungua kutoka Jupiter. Wakati Dunia iko kwenye hatua A, Dunia, Jupiter, na Io zimeunganishwa. Wakati mwingine mfungamano huu unatokea, Dunia iko kwenye hatua ya B, na nuru inayobeba habari hiyo duniani lazima iende hadi kufikia hatua hiyo. Kwa kuwa B iko mbali zaidi na Jupiter kuliko A, nuru inachukua muda mwingi kufikia Dunia wakati Dunia iko kwenye B. Sasa fikiria ni juu ya miezi 6 baadaye, na sayari hupangwa kama katika Kielelezo \(\PageIndex{1b}\). Upimaji wa kipindi cha Io unaanza na Dunia kwenye hatua ya A' na Io ikipatwa na Jupiter. Kuanguka kwa pili hutokea wakati Dunia iko kwenye hatua ya B', ambayo nuru inayobeba habari ya kupatwa hii inapaswa kusafiri. Kwa kuwa B' iko karibu na Jupiter kuliko A', nuru inachukua muda mdogo kufikia Dunia wakati iko kwenye B'. Kipindi hiki cha muda kati ya kupatwa kwa mfululizo wa Io inayoonekana kwenye A' na B' kwa hiyo ni chini ya muda kati ya kupatwa kwa kuonekana kwenye A na B. Kwa kupima tofauti katika vipindi hivi vya wakati na kwa ujuzi sahihi wa umbali kati ya Jupiter na Dunia, Roemer alihesabu kwamba kasi ya nuru ilikuwa\(2.0 \times 10^8\,m/s\), ambayo ni 33% tu chini ya thamani iliyokubaliwa leo.

Takwimu inaonyesha njia na nafasi za dunia kuhusu jua na za Io kuhusu Jupiter wakati wa kutumia njia ya Roemer. Maandalizi mawili yanaonyeshwa. Katika zote mbili, Jupiter iko kati ya Io na jua. Katika takwimu a, Dunia, Jupiter, na Io ni iliyokaa na dunia inahamia mbali na Jupiter wakati dunia iko katika eneo A, na tena katika eneo kidogo baadaye katika obiti ya dunia, B, hivyo kwamba A ni kiasi fulani karibu na Io kuliko B. katika takwimu b, maeneo mawili yanayofanana ya dunia lakini upande wa pili wa wake obiti kutoka kwa wale inavyoonekana katika takwimu a, wakati Dunia, Jupiter, na Io ni tena iliyokaa lakini dunia inahamia kuelekea Jupiter, ni lebo. kwanza ya maeneo haya ni kinachoitwa kama eneo A mkuu, na eneo baadaye kama B mkuu, ili mkuu ni kiasi fulani mbali na Io kuliko B mkuu. Mionzi ya mwanga kutoka Io hadi maeneo A, B, A mkuu, na B mkuu huonyeshwa. — Kielelezo\(\PageIndex{1}\): Njia ya angani ya Roemer ya kuamua kasi ya mwanga. Vipimo vya kipindi cha Io vinavyofanywa kwa usanidi wa sehemu (a) na (b) hutofautiana, kwa sababu urefu wa njia nyepesi na muda wa kusafiri unaohusishwa huongezeka kutoka A hadi B (a) lakini hupungua kutoka A'Ahadi B'B (b).

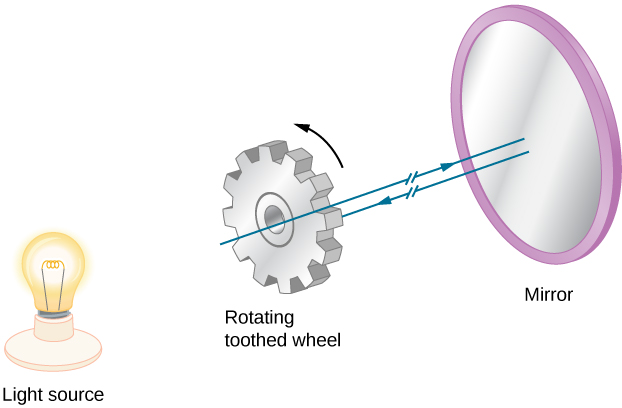
Kipimo cha kwanza cha mafanikio duniani cha kasi ya nuru kilifanywa na Armand Fizeau (1819—1896) mwaka 1849. Aliweka gurudumu la toothed ambalo linaweza kuzungushwa haraka sana kwenye kilima kimoja na kioo kwenye kilima cha pili kilima 8 mbali (Kielelezo\(\PageIndex{2}\)). Chanzo kikubwa cha mwanga kiliwekwa nyuma ya gurudumu, ili wakati gurudumu likizungushwa, limekatwa boriti ya mwanga katika mfululizo wa vurugu. Kasi ya gurudumu ilibadilishwa mpaka hakuna mwanga ulirudi kwa mwangalizi uliopo nyuma ya gurudumu. Hii inaweza tu kutokea kama gurudumu kuzungushwa kwa njia ya angle sambamba na makazi yao ya (n+½) meno, wakati kunde alisafiri chini ya kioo na nyuma. Kujua kasi ya mzunguko wa gurudumu, idadi ya meno kwenye gurudumu, na umbali wa kioo, Fizeau aliamua kasi ya mwanga kuwa\ (3.15\ mara 10 ^ 8\, m/s\), ambayo ni 5% tu ya juu sana.

Takwimu ni mfano wa kuanzisha njia ya Fizeau. Gurudumu la toothed linalozunguka liko kati ya chanzo cha mwanga (kilichoonyeshwa kama bulb ya mwanga katika mfano) na kioo. Kioo na gurudumu ni sawa na kila mmoja na perpendicular kwa boriti mwanga. Mwanga hupita kati ya meno kwenye njia ya kioo, lakini imefungwa na jino la gurudumu wakati wa kurudi kutoka kioo. — Kielelezo\(\PageIndex{2}\): Njia ya Fizeau ya kupima kasi ya mwanga. Meno ya gurudumu kuzuia mwanga yalijitokeza juu ya kurudi wakati gurudumu ni kuzungushwa kwa kiwango kwamba mechi mwanga kusafiri wakati na kutoka kioo.

Mwanafizikia wa Ufaransa Jean Bernard Léon Foucault (1819—1868) alibadilisha vifaa vya Fizeau kwa kuchukua nafasi ya gurudumu la toothed na kioo kinachozunguka. Mwaka 1862, alipima kasi ya nuru kuwa 2.98×10 ⁸ m/s, ambayo iko ndani ya 0.6% ya thamani iliyokubaliwa sasa. Albert Michelson (1852—1931) alitumia pia mbinu ya Foucault mara kadhaa ili kupima kasi ya nuru. Majaribio yake ya kwanza yalifanyika mwaka wa 1878; kufikia mwaka wa 1926, alikuwa amesafisha mbinu vizuri kiasi kwamba alikuta c kuwa (2.99796± 4) ×10 ⁸ m/s.

Leo, kasi ya mwanga inajulikana kwa usahihi mkubwa. Kwa kweli, kasi ya mwanga katika utupu c ni muhimu sana kwamba inakubaliwa kama moja ya kiasi cha msingi cha kimwili na ina thamani

\ [c=2.99792458\ mara 10 ^ 8m/s\ equiv 3.00\ mara 10 ^ 8m/s\ studio {kasi}\]

ambapo thamani ya takriban ya 3.00×10 ⁸ m/s hutumiwa wakati wowote usahihi wa tarakimu tatu unatosha.

Kasi ya Mwanga katika suala

Kasi ya nuru kupitia suala ni chini kuliko ilivyo katika utupu, kwa sababu mwanga huingiliana na atomi katika nyenzo. Kasi ya mwanga inategemea sana aina ya nyenzo, kwani mwingiliano wake unatofautiana na atomi tofauti, lattices za kioo, na miundo mingine. Tunaweza kufafanua mara kwa mara ya nyenzo zinazoelezea kasi ya mwanga ndani yake, inayoitwa index ya kukataa n:

\[n=\dfrac{c}{v} \label{index} \]

\(v\)wapi kasi ya mwanga iliyoonekana katika nyenzo.

Kwa kuwa kasi ya mwanga daima ni chini ya c katika suala na sawa c tu katika utupu, index ya kukataa daima ni kubwa kuliko au sawa na moja; yaani, n≥ 1. Jedwali\(\PageIndex{1}\) hutoa fahirisi za kukataa kwa vitu vingine vya mwakilishi. Maadili yameorodheshwa kwa wavelength fulani ya mwanga, kwa sababu hutofautiana kidogo na wavelength. (Hii inaweza kuwa na madhara muhimu, kama vile rangi zilizotengwa na mche, kama tutakavyoona katika Utawanyiko.) Kumbuka kuwa kwa gesi, n iko karibu na 1.0. Hii inaonekana kuwa ya busara, kwani atomi katika gesi zinatenganishwa sana, na mwanga husafiri kwa c katika utupu kati ya atomi. Ni kawaida kuchukua\(n=1\) gesi isipokuwa usahihi mkubwa unahitajika. Ingawa kasi ya mwanga v katika kati inatofautiana mno kutoka thamani yake c katika utupu, bado ni kasi kubwa.

Kielelezo\(\PageIndex{1}\): Ripoti ya kukataa katika vyombo vya habari mbalimbaliKwa mwanga na wavelength ya 589 nm katika utupu
Kati	n
Gesi saa 0°C, 1 atm
Air	1.000293
Dioksidi kaboni	1.00045
Hidrojeni	1.000139
Oksijeni	1.000271
Liquids saa 20°C
Benzini	1.501
Carbon disulfide	1.628
Tetrakloridi ya kaboni	1.461
Ethanol	1.361
Glycerine	1.473
Maji, safi	1.333
Yabisi katika 20°C
Almasi	2.419
Fluorite	1.434
Kioo, taji	1.52
Kioo, jiwe	1.66
Barafu (saa 0°C) 0°C)	1.309
Polystyrene	1.49
Plexiglas	1.51
Quartz, fuwele	1.544
Quartz, fused	1.458
Sodium chloride	1.544
Zircon	1.923

Mfano\(\PageIndex{1}\): Kasi ya Mwanga katika Mapambo

Tumia kasi ya mwanga katika zircon, nyenzo zilizotumiwa katika kujitia kuiga almasi.

Mkakati

Tunaweza kuhesabu kasi ya mwanga katika nyenzo\(v\) kutoka kwa ripoti\(n\) ya kukataa kwa nyenzo, kwa kutumia Equation \ red {index}

Suluhisho

Kupanga upya Equation\ ref {index} kwa\(v\) inatupa

\[v=\dfrac{c}{n}. \nonumber \]

Ripoti ya kukataa kwa zircon inapewa kama 1.923 katika Jedwali \(\PageIndex{1}\), na\(c\) imetolewa katika Equation\ ref {kasi}. Kuingia maadili haya katika equation inatoa

\ [kuanza {align*} v &=\ dfrac {3.00×10 ^ 8m/s} {1.923}\ [4pt] &= 1.56×10 ^ 8m/s.\ mwisho {align*}\ nonnumber\]

Umuhimu

Kasi hii ni kubwa kidogo kuliko nusu kasi ya mwanga katika utupu na bado ni ya juu ikilinganishwa na kasi sisi kawaida uzoefu. Dutu pekee iliyoorodheshwa katika Jedwali\(\PageIndex{1}\) ambayo ina index kubwa ya kukataa kuliko zircon ni almasi. Tutaona baadaye kwamba ripoti kubwa ya kukataa kwa zircon inafanya kuangaza zaidi ya kioo, lakini chini ya almasi.

Zoezi\(\PageIndex{1}\)

Jedwali \(\PageIndex{1}\) linaonyesha kwamba ethanol na maji safi vina fahirisi sawa za kukataa. Kwa asilimia gani kasi ya mwanga katika maji haya yanatofautiana?

Jibu: 2.1% (kwa takwimu mbili muhimu)

Mfano wa Ray wa Mwanga

Tayari umejifunza baadhi ya sifa za wimbi la mwanga katika sura ya awali juu ya Mawimbi ya umeme. Katika sura hii, tunaanza hasa na sifa za ray. Kuna njia tatu ambazo mwanga unaweza kusafiri kutoka chanzo hadi mahali pengine (Kielelezo \(\PageIndex{1}\)). Inaweza kuja moja kwa moja kutoka chanzo kupitia nafasi tupu, kama vile kutoka Jua hadi Dunia. Au mwanga unaweza kusafiri kupitia vyombo vya habari mbalimbali, kama vile hewa na kioo, kwa mwangalizi. Mwanga unaweza pia kufika baada ya kuonekana, kama vile kioo. Katika matukio haya yote, tunaweza kuiga njia ya mwanga kama mstari wa moja kwa moja unaoitwa ray.

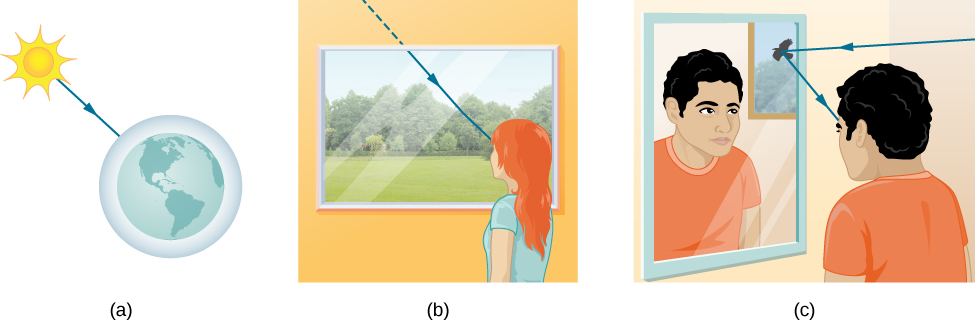
Takwimu ina michoro inayoonyesha mbinu tatu za mwanga kusafiri kutoka chanzo hadi mahali pengine. Kielelezo a inaonyesha mwanga kutoka jua kufikia anga ya dunia, kusafiri katika mstari wa moja kwa moja kupitia nafasi. Kielelezo b umeonyesha mwanga kusafiri kupitia dirisha kufikia mwangalizi. Kielelezo c inaonyesha mwanga kusafiri kutoka kitu kwa kioo na kutafakari kuelekea mwangalizi. — Kielelezo\(\PageIndex{3}\): Njia tatu za mwanga kusafiri kutoka chanzo hadi mahali pengine. (a) Mwanga hufikia anga ya juu ya Dunia, ikisafiri kupitia nafasi tupu moja kwa moja kutoka chanzo. (b) Mwanga unaweza kumfikia mtu kwa kusafiri kupitia vyombo vya habari kama hewa na kioo. (c) Mwanga pia unaweza kutafakari kutoka kwenye kitu kama kioo. Katika hali zilizoonyeshwa hapa, mwanga huingiliana na vitu vingi vya kutosha kwamba husafiri katika mistari ya moja kwa moja, kama ray.

Majaribio yanaonyesha kwamba wakati mwanga unapoingiliana na kitu mara kadhaa kubwa kuliko wavelength yake, husafiri katika mistari ya moja kwa moja na hufanya kama ray. Tabia zake za wimbi hazijulikani katika hali kama hizo. Kwa kuwa wavelength ya mwanga inayoonekana ni chini ya micron (elfu ya millimeter), hufanya kama ray katika hali nyingi za kawaida ambazo hukutana na vitu vingi zaidi kuliko micron. Kwa mfano, wakati mwanga unaoonekana unakabiliwa na kitu chochote kikubwa cha kutosha ili tuweze kuiangalia kwa macho yasiyosaidiwa, kama sarafu, hufanya kama ray, na sifa za wimbi la kawaida.

Katika matukio haya yote, tunaweza kuiga njia ya mwanga kama mistari ya moja kwa moja. Mwanga huweza kubadilisha mwelekeo unapokutana na vitu (kama vile kioo) au kwa kupita kutoka nyenzo moja hadi nyingine (kama vile kwa kupita kutoka hewa hadi kioo), lakini kisha unaendelea katika mstari wa moja kwa moja au kama ray. Neno “ray” linatokana na hisabati na hapa linamaanisha mstari wa moja kwa moja unaoanzia wakati fulani. Ni kukubalika kutazama mionzi ya mwanga kama mionzi ya laser. Mfano wa mwanga wa mwanga unaelezea njia ya nuru kama mistari ya moja kwa moja.

Kwa kuwa mwanga huenda kwenye mistari ya moja kwa moja, kubadilisha maelekezo wakati unapoingiliana na vifaa, njia yake inaelezwa na jiometri na trigonometry rahisi. Sehemu hii ya optics, ambapo kipengele cha ray cha mwanga kinatawala, kinaitwa optics ya kijiometri. Sheria mbili zinatawala jinsi mwanga hubadilisha mwelekeo unapoingiliana na jambo. Hizi ni sheria ya kutafakari, kwa hali ambazo mwanga huzuia jambo, na sheria ya kukataa, kwa hali ambazo mwanga hupita kupitia jambo. Sisi kuchunguza zaidi kuhusu kila moja ya sheria hizi katika sehemu ujao wa sura hii.