Skip to main content
Global

11.4E: Mazoezi

  1. Last updated
  2. Save as PDF
  • Page ID
    176896

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mazoezi hufanya kamili

    Zoezi\(\PageIndex{15}\) Graph an Ellipse with Center at the Origin

    Katika mazoezi yafuatayo, grafu kila duaradufu.

    1. \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    3. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    4. \(\frac{x^{2}}{16}+\frac{y^{2}}{36}=1\)
    5. \(\frac{x^{2}}{36}+\frac{y^{2}}{16}=1\)
    6. \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
    7. \(x^{2}+\frac{y^{2}}{4}=1\)
    8. \(\frac{x^{2}}{9}+y^{2}=1\)
    9. \(4 x^{2}+25 y^{2}=100\)
    10. \(16 x^{2}+9 y^{2}=144\)
    11. \(16 x^{2}+36 y^{2}=576\)
    12. \(9 x^{2}+25 y^{2}=225\)
    Jibu

    1.

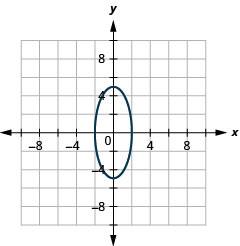
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (0, 5) na (0, hasi 5) na mwisho wa mhimili mdogo (2, 0) na (hasi 2, 0).
    Kielelezo 11.3.38

    3.

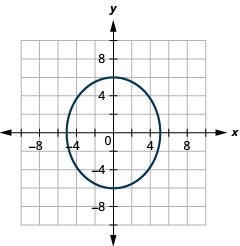
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (0, 6) na (0, hasi 6) na mwisho wa mhimili mdogo (5, 0) na (hasi 5, 0).
    Kielelezo 11.3.39

    5.

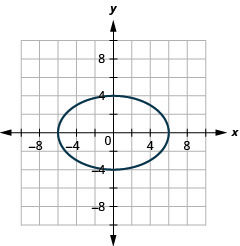
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (6, 0) na (hasi 6, 0) na mwisho wa mhimili mdogo (0, 4) na (0, hasi 4).
    Kielelezo 11.3.40

    7.

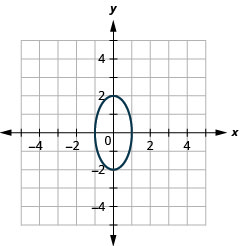
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (0, 2) na (0, hasi 2) na mwisho wa mhimili mdogo (1, 0) na (hasi 1, 0).
    Kielelezo 11.3.41

    9.

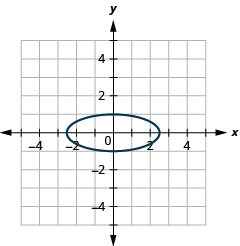
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (5, 0) na (hasi 5, 0) na mwisho wa mhimili mdogo (0, 2) na (0, hasi 2).
    Kielelezo 11.3.42

    11.

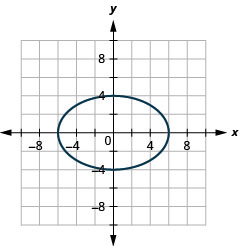
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (6, 0) na (hasi 6, 0) na mwisho wa mhimili mdogo (0, 4) na (0, hasi 4).
    Kielelezo 11.3.43
    Zoezi\(\PageIndex{16}\) Find the Equation of an Ellipse with Center at the Origin

    Katika mazoezi yafuatayo, pata equation ya ellipse iliyoonyeshwa kwenye grafu.

    1.

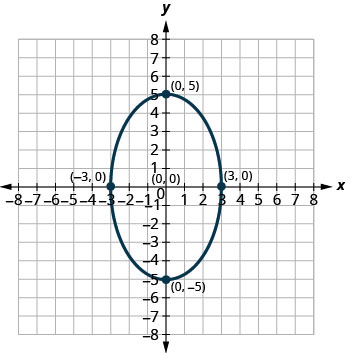
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (0, 5) na (0, hasi 5) na mwisho wa mhimili mdogo (hasi 3, 0) na (3, 0).
    Kielelezo 11.3.44

    2.

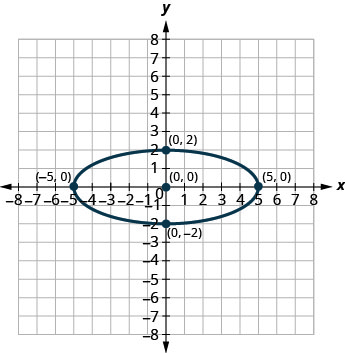
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (5, 0) na (hasi 5, 0) na mwisho wa mhimili mdogo (0, 2) na (0, hasi 2).
    Kielelezo 11.3.45

    3.

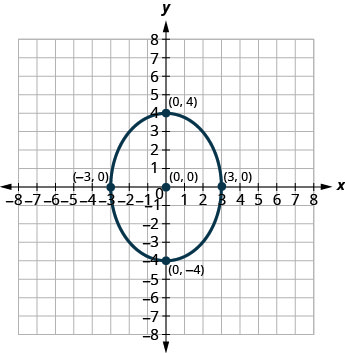
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (0, 4) na (0, hasi 4) na mwisho wa mhimili mdogo (hasi 3, 0) na (3, 0).
    Kielelezo 11.3.46

    4.

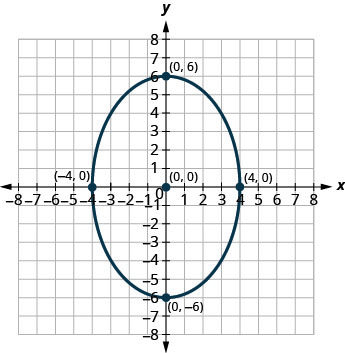
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (0, 6) na (0, hasi 6) na mwisho wa mhimili mdogo (hasi 4, 0) na (4, 0).
    Kielelezo 11.3.47
    Jibu

    1. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)

    3. \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)

    Zoezi\(\PageIndex{17}\) Graph an Ellipse with Center Not at the Origin

    Katika mazoezi yafuatayo, grafu kila duaradufu.

    1. \(\frac{(x+1)^{2}}{4}+\frac{(y+6)^{2}}{25}=1\)
    2. \(\frac{(x-3)^{2}}{25}+\frac{(y+2)^{2}}{9}=1\)
    3. \(\frac{(x+4)^{2}}{4}+\frac{(y-2)^{2}}{9}=1\)
    4. \(\frac{(x-4)^{2}}{9}+\frac{(y-1)^{2}}{16}=1\)
    Jibu

    1.

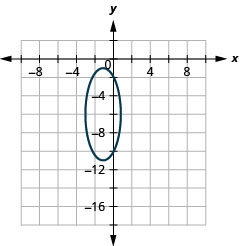
    Grafu hii inaonyesha duaradufu na kituo cha (hasi 1, hasi 6, vipeo (hasi 1, hasi 1) na (hasi 1, hasi 11) na mwisho wa mhimili mdogo (hasi 3, hasi 6) na (1, hasi 6).
    Kielelezo 11.3.48

    3.

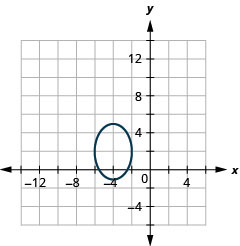
    Grafu hii inaonyesha duaradufu na kituo cha (hasi 4, 2, vipeo (hasi 4, 5) na (hasi 4, hasi 1) na mwisho wa mhimili mdogo (3, 1) na (hasi 6, 2) na (hasi 2, 2) na (hasi 2, 2).
    Kielelezo 11.3.49
    Zoezi\(\PageIndex{18}\) Graph an Ellipse with Center Not at the Origin

    Katika mazoezi yafuatayo, graph kila equation kwa tafsiri.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
    2. \(\frac{(x+6)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
    3. \(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{25}=1\)
    4. \(\frac{(x+5)^{2}}{36}+\frac{(y-3)^{2}}{16}=1\)
    Jibu

    1.

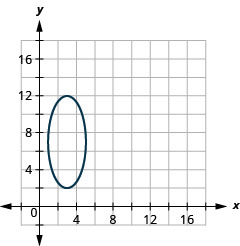
    Grafu hii inaonyesha duaradufu na kituo cha (3, 7), vipeo (3, 2) na (3, 12), na mwisho wa mhimili mdogo (1, 7) na (5, 7).
    Kielelezo 11.3.50

    3.

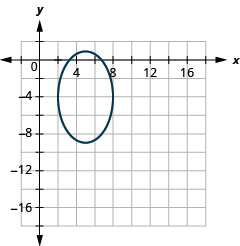
    Grafu hii inaonyesha duaradufu na kituo cha (5, hasi 4), vipeo (5, 1) na (5, hasi 9) na mwisho wa mhimili mdogo (2, hasi 4) na (8, hasi 4).
    Kielelezo 11.3.51
    Zoezi\(\PageIndex{19}\) Graph an Ellipse with Center Not at the Origin

    Katika mazoezi yafuatayo,

    1. Andika equation katika fomu ya kawaida na
    2. Grafu.
    1. \(25 x^{2}+9 y^{2}-100 x-54 y-44=0\)
    2. \(4 x^{2}+25 y^{2}+8 x+100 y+4=0\)
    3. \(4 x^{2}+25 y^{2}-24 x-64=0\)
    4. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    Jibu

    1.

    1. \(\frac{(x-2)^{2}}{9}+\frac{(y-3)^{2}}{25}=1\)
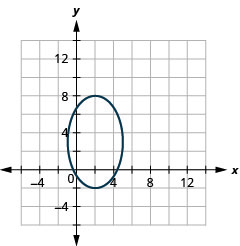
    Grafu hii inaonyesha duaradufu na kituo cha (2, 3), vipeo (2, hasi 2) na (2, 8) na mwisho wa mhimili mdogo (hasi 1, 3) na (5, 3).
    Kielelezo 11.3.52

    3.

    1. \(\frac{y^{2}}{4}+\frac{(x-3)^{2}}{25}=1\)
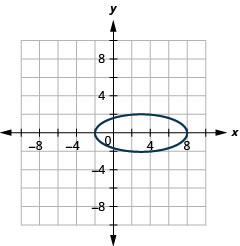
    Grafu hii inaonyesha duaradufu na kituo cha (3, 0), vipeo (hasi 2, 0) na (8, 0) na mwisho wa mhimili mdogo (3, 2) na (3, hasi 2).
    Kielelezo 11.3.53
    Zoezi\(\PageIndex{20}\) Graph an Ellipse with Center Not at the Origin

    Katika mazoezi yafuatayo, graph equation.

    1. \(x=-2(y-1)^{2}+2\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \(y=-x^{2}+8 x-15\)
    5. \(\frac{(x+3)^{2}}{16}+\frac{(y+1)^{2}}{4}=1\)
    6. \((x-2)^{2}+(y-3)^{2}=9\)
    7. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    8. \(x=4(y+1)^{2}-4\)
    9. \(x^{2}+y^{2}=64\)
    10. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    11. \(y=6 x^{2}+2 x-1\)
    12. \(\frac{(x-2)^{2}}{9}+\frac{(y+3)^{2}}{25}=1\)
    Jibu

    1.

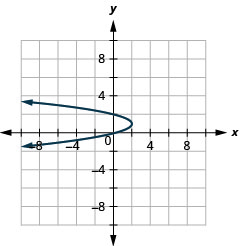
    Grafu hii inaonyesha parabola na kipeo (2, 1) na y intercepts (0, 0) na (2, 0).
    Kielelezo 11.3.54

    3.

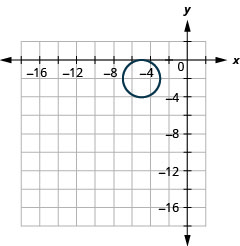
    Grafu hii inaonyesha mduara na kituo (hasi 5, hasi 2) na radius ya vitengo 2.
    Kielelezo 11.3.55

    5.

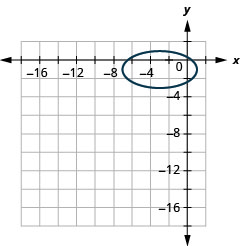
    Grafu hii inaonyesha duaradufu na kituo cha (hasi 3, hasi 1), vipeo (1, hasi 1) na (hasi 7, hasi 1) na mwisho wa mhimili mdogo (hasi 3, 1) na (hasi 3, hasi 3).
    Kielelezo 11.3.56

    7.

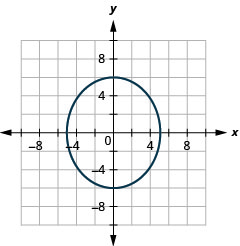
    Grafu hii inaonyesha duaradufu na kituo cha (0, 0), vipeo (0, 6) na (0, hasi 6) na mwisho wa mhimili mdogo (hasi 5, 0) na (5, 0).
    Kielelezo 11.3.57

    9.

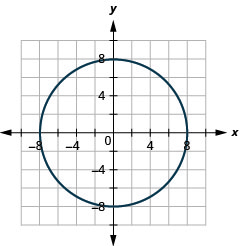
    Grafu hii inaonyesha mduara na kituo cha (0, 0) na kwa Radius 8 vitengo.
    Kielelezo 11.3.58

    11.

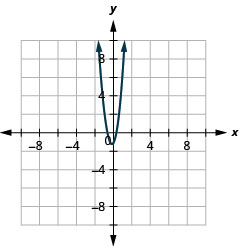
    Grafu hii inaonyesha juu ya ufunguzi parabola. Vertex yake ina thamani x ya kidogo chini ya 0 na thamani y ya kidogo chini ya minus 1. Hatua juu yake ni takriban saa (hasi 1, 3).
    Kielelezo 11.3.59
    Zoezi\(\PageIndex{21}\) Solve Application with Ellipses

    1. Sayari inakwenda katika obiti ya duaradufu kuzunguka jua lake. Karibu zaidi sayari inapata jua ni takriban\(10\) AU na iliyo mbali zaidi ni takriban\(30\) AU. Jua ni moja ya foci ya obiti ya elliptical. Kuruhusu kituo cha ellipse katika asili na kuandika axes katika AU, obiti itaonekana kama takwimu hapa chini. Tumia grafu kuandika equation kwa obiti elliptical ya sayari.

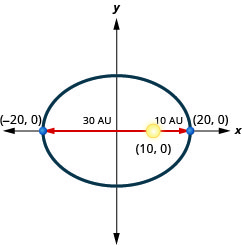
    Grafu hii inaonyesha duaradufu na kituo (0, 0), vertices (hasi 20, 0) na (20, 0). Jua linaonyeshwa kwenye hatua (10, 0), ambayo ni vitengo 30 kutoka vertex ya kushoto na vitengo 10 kutoka vertex sahihi.
    Kielelezo 11.3.60

    2. Sayari inakwenda katika obiti ya duaradufu kuzunguka jua lake. Karibu zaidi sayari inapata jua ni takriban\(10\) AU na iliyo mbali zaidi ni takriban\(70\) AU. Jua ni moja ya foci ya obiti ya elliptical. Kuruhusu kituo cha ellipse katika asili na kuandika axes katika AU, obiti itaonekana kama takwimu hapa chini. Tumia grafu kuandika equation kwa obiti elliptical ya sayari.

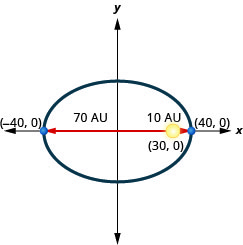
    Grafu hii inaonyesha duaradufu na kituo (0, 0), vertices (hasi 40, 0) na (40, 0). Jua linaonyeshwa kwenye hatua (30, 0), ambayo ni vitengo 70 kutoka vertex ya kushoto na vitengo 10 kutoka vertex sahihi.
    Kielelezo 11.3.61

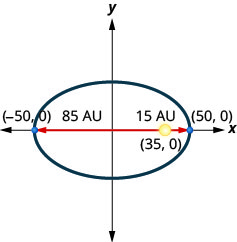
    3. Comet huenda katika obiti ya elliptical karibu na jua. Karibu zaidi kimondo kinapata jua ni takriban\(15\) AU na mbali zaidi ni takriban\(85\) AU. Jua ni moja ya foci ya obiti ya elliptical. Kuruhusu kituo cha ellipse katika asili na kuandika axes katika AU, obiti itaonekana kama takwimu hapa chini. Tumia grafu kuandika equation kwa obiti elliptical ya comet.

    Grafu hii inaonyesha duaradufu na kituo (0, 0), vertices (hasi 50, 0) na (50, 0). Jua linaonyeshwa kwenye hatua (35, 0), ambayo ni vitengo 85 kutoka vertex ya kushoto na vitengo 15 kutoka vertex sahihi.
    Kielelezo 11.3.62

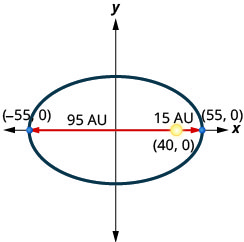
    4. Comet huenda katika obiti ya elliptical karibu na jua. Karibu zaidi kimondo kinapata jua ni takriban\(15\) AU na mbali zaidi ni takriban\(95\) AU. Jua ni moja ya foci ya obiti ya elliptical. Kuruhusu kituo cha ellipse katika asili na kuandika axes katika AU, obiti itaonekana kama takwimu hapa chini. Tumia grafu kuandika equation kwa obiti elliptical ya comet.

    Grafu hii inaonyesha duaradufu na kituo (0, 0), vertices (hasi 55, 0) na (55, 0). Jua linaonyeshwa kwenye hatua (40, 0), ambayo ni vitengo 95 kutoka vertex ya kushoto na vitengo 15 kutoka vertex sahihi.
    Kielelezo 11.3.63
    Jibu

    1. \(\frac{x^{2}}{400}+\frac{y^{2}}{300}=1\)

    3. \(\frac{x^{2}}{2500}+\frac{y^{2}}{1275}=1\)

    Zoezi\(\PageIndex{22}\) Writing Exercises
    1. Kwa maneno yako mwenyewe, fafanua duaradufu na uandike usawa wa duaradufu unaozingatia asili katika fomu ya kawaida. Chora mchoro wa ellipse kuipatia katikati, vertices na axes kuu na ndogo.
    2. Eleza kwa maneno yako mwenyewe jinsi ya kupata shaba kutoka kwa equation katika fomu ya kawaida.
    3. Linganisha na kulinganisha grafu ya equations\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) na\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\).
    4. Eleza kwa maneno yako mwenyewe, tofauti kati ya vertex na lengo la ellipse.
    Jibu

    1. Majibu inaweza kutofautiana

    3. Majibu inaweza kutofautiana

    Self Check

    Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

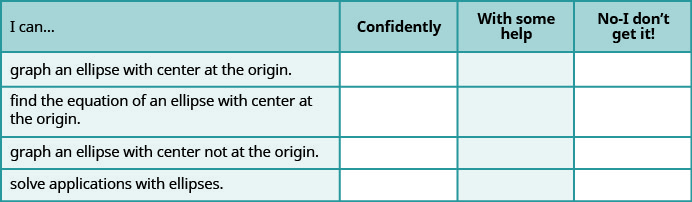
    Jedwali hili lina safu 4 safu 4 na mstari wa kichwa. Mstari wa kichwa huandika kila safu ninaweza, kwa ujasiri, kwa msaada fulani na hapana, sijui €™ t kupata. Nguzo za kwanza zina taarifa zifuatazo: graph duaradufu na kituo cha asili, kupata equation ya duaradufu na kituo cha asili, grafu duaradufu na kituo cha si asili, kutatua maombi na ellipses. Nguzo zilizobaki ni tupu.
    Kielelezo 11.3.64

    b Orodha hii inakuambia nini kuhusu ujuzi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?