Skip to main content
Global

9.8E: Mazoezi

  1. Last updated
  2. Save as PDF
  • Page ID
    176497

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mazoezi hufanya kamili

    Zoezi\(\PageIndex{23}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}=k\)

    Katika mazoezi yafuatayo,

    1. Grafu kazi za quadratic kwenye mfumo huo wa kuratibu mstatili
    2. Eleza nini athari kuongeza mara kwa mara\(k\),, kwa kazi ina juu ya parabola msingi.
      1. \(f(x)=x^{2}, g(x)=x^{2}+4, \text { and } h(x)=x^{2}-4\)
      2. \(f(x)=x^{2}, g(x)=x^{2}+7, \text { and } h(x)=x^{2}-7\)
    Jibu

    1.


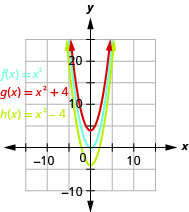
    1. Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve katikati ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve juu imekuwa wakiongozwa hadi 4 vitengo, na chini imekuwa wakiongozwa chini 4 vitengo.
      Kielelezo 9.7.71
    2. Grafu ya\(g(x)=x^{2}+4\) ni sawa na grafu ya\(4\) vitengo\(f(x)=x^{2}\) lakini vilivyobadilishwa. Grafu ya\(h(x)=x^{2}-4\) ni sawa na grafu ya\(f(x)=x^{2}\) lakini kuhama chini\(4\) vitengo.
    Zoezi\(\PageIndex{24}\) Graph Quadratic Functions of the Form \(f(x)=x^{2}=k\)

    Katika mazoezi yafuatayo, grafu kila kazi kwa kutumia mabadiliko ya wima.

    1. \(f(x)=x^{2}+3\)
    2. \(f(x)=x^{2}-7\)
    3. \(g(x)=x^{2}+2\)
    4. \(g(x)=x^{2}+5\)
    5. \(h(x)=x^{2}-4\)
    6. \(h(x)=x^{2}-5\)
    Jibu

    1.

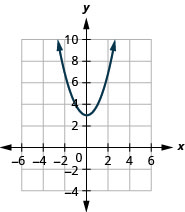
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (0, 3) na pointi nyingine (7, 2) na (7, hasi 2).
    Kielelezo 9.7.72

    3.

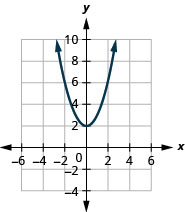
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (0, 2) na pointi nyingine (hasi 2, 6) na (2, 6).
    Kielelezo 9.7.73

    5.

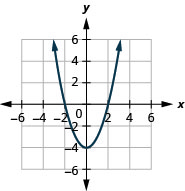
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (0, hasi 4) na pointi nyingine (hasi 2, 0) na (2, 0).
    Kielelezo 9.7.74
    Zoezi\(\PageIndex{25}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    Katika mazoezi yafuatayo,

    1. Grafu kazi za quadratic kwenye mfumo huo wa kuratibu mstatili
    2. Eleza nini athari kuongeza mara kwa mara\(h\), ndani ya mabano ina
      1. \(f(x)=x^{2}, g(x)=(x-3)^{2}, \text { and } h(x)=(x+3)^{2}\)
      2. \(f(x)=x^{2}, g(x)=(x+4)^{2}, \text { and } h(x)=(x-4)^{2}\)
    Jibu

    1.


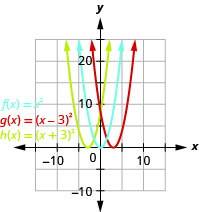
    1. Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Moja ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Grafu ya kulia imebadilishwa vitengo 3 kwa haki ya kuzalisha g ya x sawa na kiasi cha x minus 3 squared. Grafu ya kushoto imebadilishwa vitengo 3 upande wa kushoto ili kuzalisha h ya x sawa na kiasi cha x pamoja na 3 mraba.
      Kielelezo 9.7.75
    2. Grafu ya\(g(x)=(x−3)^{2}\) ni sawa na grafu ya\(3\) vitengo vya haki\(f(x)=x^{2}\) lakini vilivyobadilishwa. Grafu ya\(h(x)=(x+3)^{2}\) ni sawa na grafu ya\(3\) vitengo vya kushoto\(f(x)=x^{2}\) lakini vilivyobadilishwa.
    Zoezi\(\PageIndex{26}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    Katika mazoezi yafuatayo, grafu kila kazi kwa kutumia mabadiliko ya usawa.

    1. \(f(x)=(x-2)^{2}\)
    2. \(f(x)=(x-1)^{2}\)
    3. \(f(x)=(x+5)^{2}\)
    4. \(f(x)=(x+3)^{2}\)
    5. \(f(x)=(x-5)^{2}\)
    6. \(f(x)=(x+2)^{2}\)
    Jibu

    1.

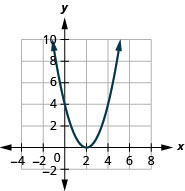
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina kipeo cha (2, 0) na pointi nyingine (0, 4) na (4, 4).
    Kielelezo 9.7.76

    3.

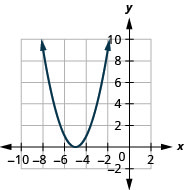
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (hasi 5, 0) na pointi nyingine (hasi 7, 4) na (hasi 3, 4).
    Kielelezo 9.7.77

    5.

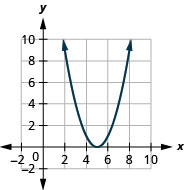
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina kipeo cha (5, 0) na pointi nyingine (3, 4) na (7, 4).
    Kielelezo 9.7.78
    Zoezi\(\PageIndex{27}\) Graph Quadratic Functions of the Form \(f(x)=(x-h)^{2}\)

    Katika mazoezi yafuatayo, grafu kila kazi kwa kutumia mabadiliko.

    1. \(f(x)=(x+2)^{2}+1\)
    2. \(f(x)=(x+4)^{2}+2\)
    3. \(f(x)=(x-1)^{2}+5\)
    4. \(f(x)=(x-3)^{2}+4\)
    5. \(f(x)=(x+3)^{2}-1\)
    6. \(f(x)=(x+5)^{2}-2\)
    7. \(f(x)=(x-4)^{2}-3\)
    8. \(f(x)=(x-6)^{2}-2\)
    Jibu

    1.

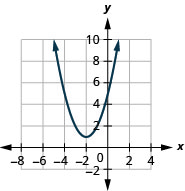
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (hasi 2, 1) na pointi nyingine (hasi 4, 5) na (0, 5).
    Kielelezo 9.7.79

    3.

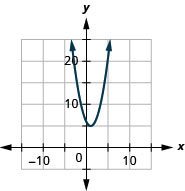
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (1, 5) na pointi nyingine (hasi 1, 9) na (3, 9).
    Kielelezo 9.7.80

    5.

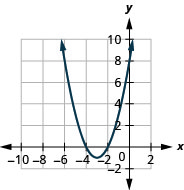
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (hasi 3, 1) na pointi nyingine (hasi 4, 0) na (hasi 2, 0).
    Kielelezo 9.7.81

    7.

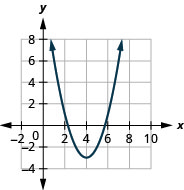
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (4, hasi 2) na pointi nyingine (3, hasi 2) na (5, hasi 2).
    Kielelezo 9.7.82
    Zoezi\(\PageIndex{28}\) Graph Quadratic Functions of the Form \(f(x)=ax^{2}\)

    Katika mazoezi yafuatayo, grafu kila kazi.

    1. \(f(x)=-2 x^{2}\)
    2. \(f(x)=4 x^{2}\)
    3. \(f(x)=-4 x^{2}\)
    4. \(f(x)=-x^{2}\)
    5. \(f(x)=\frac{1}{2} x^{2}\)
    6. \(f(x)=\frac{1}{3} x^{2}\)
    7. \(f(x)=\frac{1}{4} x^{2}\)
    8. \(f(x)=-\frac{1}{2} x^{2}\)
    Jibu

    1.

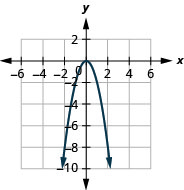
    Takwimu hii inaonyesha parabolas ya kufungua chini kwenye ndege ya kuratibu x y. Ina vertex ya (0, 0) na pointi nyingine (hasi 1, hasi 2) na (1, hasi 2).
    Kielelezo 9.7.83

    3.

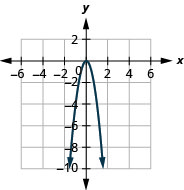
    Takwimu hii inaonyesha parabolas ya kufungua chini kwenye ndege ya kuratibu x y. Ina vertex ya (0, 0) na pointi nyingine (hasi 1, hasi 4) na (1, hasi 4).
    Kielelezo 9.7.84

    5.

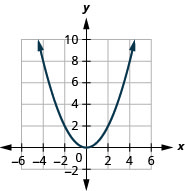
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (0, 0) na pointi nyingine (hasi 2, 2) na (2, 2).
    Kielelezo 9.7.85

    7.

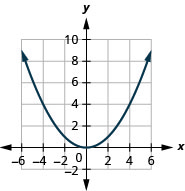
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina vertex ya (0, 0) na pointi nyingine (2, 1) na (hasi 2, 1).
    Kielelezo 9.7.86
    Zoezi\(\PageIndex{29}\) Graph Quadratic Functions Using Transformations

    Katika mazoezi yafuatayo, fungua upya kila kazi kwa\(f(x)=a(x−h)^{2}+k\) fomu kwa kukamilisha mraba.

    1. \(f(x)=-3 x^{2}-12 x-5\)
    2. \(f(x)=2 x^{2}-12 x+7\)
    3. \(f(x)=3 x^{2}+6 x-1\)
    4. \(f(x)=-4 x^{2}-16 x-9\)
    Jibu

    1. \(f(x)=-3(x+2)^{2}+7\)

    3. \(f(x)=3(x+1)^{2}-4\)

    Zoezi\(\PageIndex{30}\) Graph Quadratic Functions Using Transformations

    Katika mazoezi yafuatayo,

    1. Andika upya kila kazi kwa\(f(x)=a(x−h)^{2}+k\) fomu
    2. Grafu kwa kutumia mabadiliko
      1. \(f(x)=x^{2}+6 x+5\)
      2. \((x)=x^{2}+4 x-12\)
      3. \(f(x)=x^{2}+4 x-12\)
      4. \(f(x)=x^{2}-6 x+8\)
      5. \(f(x)=x^{2}-6 x+15\)
      6. \(f(x)=x^{2}+8 x+10\)
      7. \(f(x)=-x^{2}+8 x-16\)
      8. \(f(x)=-x^{2}+2 x-7\)
      9. \(f(x)=-x^{2}-4 x+2\)
      10. \(f(x)=-x^{2}+4 x-5\)
      11. \(f(x)=5 x^{2}-10 x+8\)
      12. \(f(x)=3 x^{2}+18 x+20\)
      13. \(f(x)=2 x^{2}-4 x+1\)
      14. \(f(x)=3 x^{2}-6 x-1\)
      15. \(f(x)=-2 x^{2}+8 x-10\)
      16. \(f(x)=-3 x^{2}+6 x+1\)
    Jibu

    1.

    1. f (x) = (x+3) ^ {2} -4
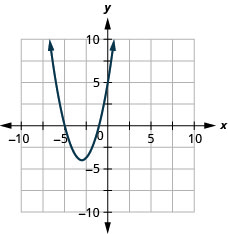
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina kipeo cha (hasi 3, 3), y-intercept ya (0, 5), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na hasi 3.
    Kielelezo 9.7.87

    3.

    1. \(f(x)=(x+2)^{2}-1\)
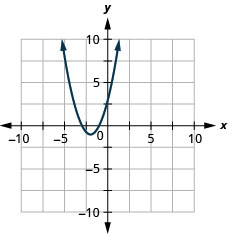
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina kipeo cha (hasi 2, hasi 1), y-intercept ya (0, 3), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na hasi 2.
    Kielelezo 9.7.88

    5.

    1. \(f(x)=(x-3)^{2}+6\)
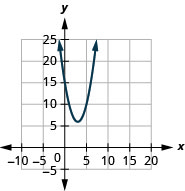
    Takwimu hii inaonyesha parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Ina kipeo cha (3, 6), y-intercept ya (0, 10), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na 3.
    Kielelezo 9.7.89

    7.

    1. \(f(x)=-(x-4)^{2}+0\)
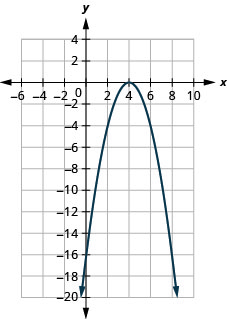
    Takwimu hii inaonyesha parabola ya kufungua chini kwenye ndege ya kuratibu x y. Ina kipeo cha (4, 0), y-intercept ya (0, hasi 16), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na 4.
    Kielelezo 9.7.90

    9.

    1. \(f(x)=-(x+2)^{2}+6\)
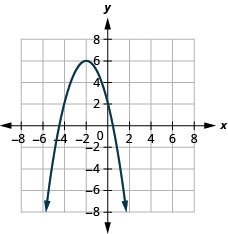
    Takwimu hii inaonyesha parabola ya kufungua chini kwenye ndege ya kuratibu x y. Ina kipeo cha (hasi 2, 6), y-intercept ya (0, 2), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na hasi 2.
    Kielelezo 9.7.91

    11.

    1. \(f(x)=5(x-1)^{2}+3\)
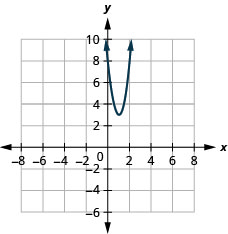
    Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina kipeo cha (1, 3), y-intercept ya (0, 8), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na 1.
    Kielelezo 9.7.92

    13.

    1. \(f(x)=2(x-1)^{2}-1\)
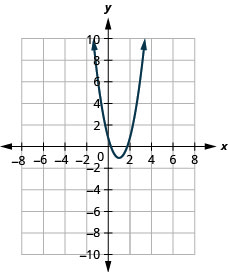
    Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina kipeo cha (1, hasi 1), y-intercept ya (0, 1), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na 1.
    Kielelezo 9.7.93

    15.

    1. \(f(x)=-2(x-2)^{2}-2\)
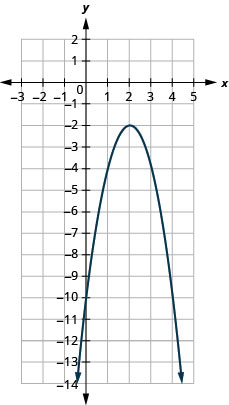
    Takwimu hii inaonyesha parabola ya kufungua chini kwenye ndege ya kuratibu x y. Ina kipeo cha (2, hasi 2), y-intercept ya (0, hasi 10), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na 2.
    Kielelezo 9.7.94
    Zoezi\(\PageIndex{31}\) Graph Quadratic Functions Using Transformations

    Katika mazoezi yafuatayo,

    1. Andika upya kila kazi kwa\(f(x)=a(x−h)^{2}+k\) fomu
    2. Grafu kwa kutumia mali
      1. \(f(x)=2 x^{2}+4 x+6\)
      2. \(f(x)=3 x^{2}-12 x+7\)
      3. \(f(x)=-x^{2}+2 x-4\)
      4. \(f(x)=-2 x^{2}-4 x-5\)
    Jibu

    1.

    1. \(f(x)=2(x+1)^{2}+4\)
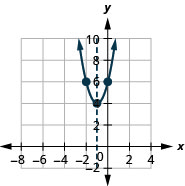
    Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina kipeo cha (hasi 1, 4), y-intercept ya (0, 6), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na hasi 1.
    Kielelezo 9.7.95

    3.

    1. \(f(x)=-(x-1)^{2}-3\)
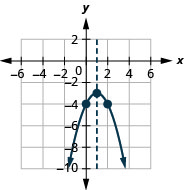
    Takwimu hii inaonyesha parabola ya kufungua chini kwenye ndege ya kuratibu x y. Ina kipeo cha (1, hasi 3), y-intercept ya (0, hasi 4), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na 1.
    Kielelezo 9.7.96
    Zoezi\(\PageIndex{32}\) Matching

    Katika mazoezi yafuatayo, mechi ya grafu kwa moja ya kazi zifuatazo:

    1. \(f(x)=x^{2}+4\)
    2. \(f(x)=x^{2}-4\)
    3. \(f(x)=(x+4)^{2}\)
    4. \(f(x)=(x-4)^{2}\)
    5. \(f(x)=(x+4)^{2}-4\)
    6. \(f(x)=(x+4)^{2}+4\)
    7. \(f(x)=(x-4)^{2}-4\)
    8. \(f(x)=(x-4)^{2}+4\)

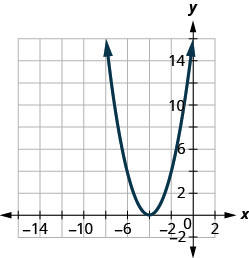
      1. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (hasi 4, 0) na pointi nyingine (hasi 4, 4) na (hasi 2, 4).
        Kielelezo 9.7.97

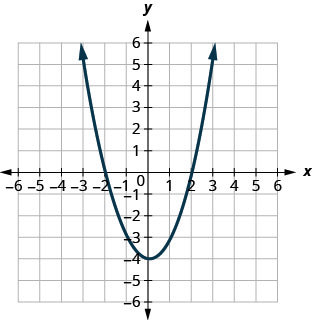
      2. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (0, hasi 4) na pointi nyingine (hasi 2, 0) na (2, 0).
        Kielelezo 9.7.98

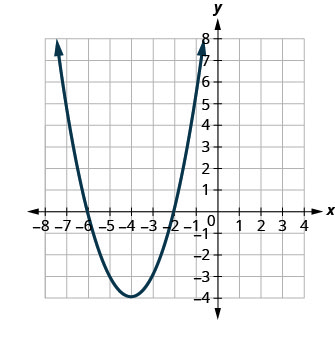
      3. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (hasi 4, hasi 4) na pointi nyingine (hasi 4, 0) na (hasi 2, 0).
        Kielelezo 9.7.99

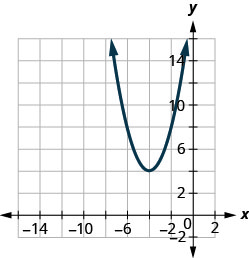
      4. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (hasi 4, 4) na pointi nyingine (hasi 6, 8) na (hasi 2, 8).
        Kielelezo 9.7.100

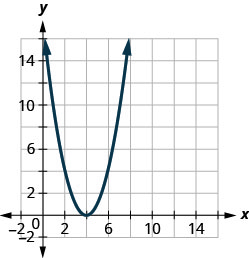
      5. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina kipeo cha (4, 0) na pointi nyingine (2, 4) na (2, 4).
        Kielelezo 9.7.101

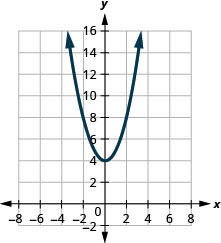
      6. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (0, 4) na pointi nyingine (hasi 2, 8) na (2, 8).
        Kielelezo 9.7.102

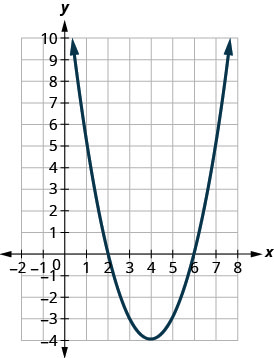
      7. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina kipeo cha (4, hasi 4) na pointi nyingine (2,0) na (6,0).
        Kielelezo 9.7.103

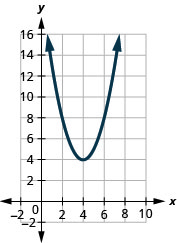
      8. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina kipeo cha (4, 4) na pointi nyingine (2,8) na (6,8).
        Kielelezo 9.7.104
    Jibu

    1. c

    3. e

    5. d

    7. g

    Zoezi\(\PageIndex{33}\) Find a Quadratic Function from its Graph

    Katika mazoezi yafuatayo, weka kazi ya quadratic kwa\(f(x)=a(x−h)^{2}+k\) fomu ambayo grafu inavyoonyeshwa.


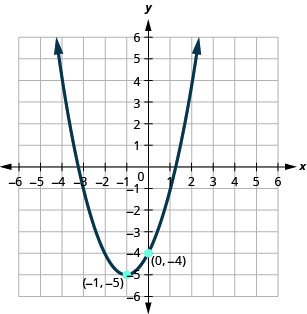
    1. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (hasi 1, hasi 5) na y-intercept (0, hasi 4).
      Kielelezo 9.7.105

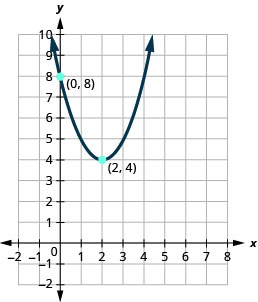
    2. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina kipeo cha (2,4) na y-intercept (0, 8).
      Kielelezo 9.7.106

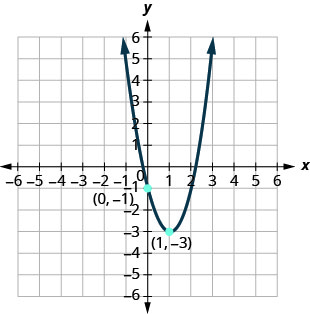
    3. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (1, hasi 3) na y-intercept (0, hasi 1).
      Kielelezo 9.7.107

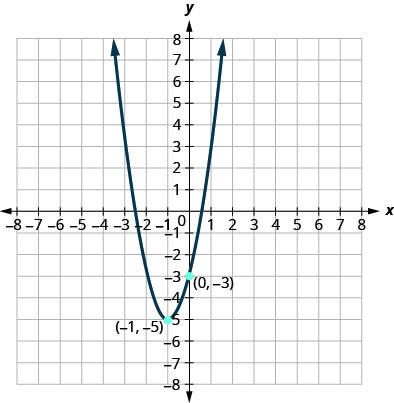
    4. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (hasi 1, hasi 5) na y-intercept (0, hasi 3).
      Kielelezo 9.7.108
    Jibu

    1. \(f(x)=(x+1)^{2}-5\)

    3. \(f(x)=2(x-1)^{2}-3\)

    Zoezi\(\PageIndex{34}\) Writing Exercise
    1. Graph kazi ya quadratic\(f(x)=x^{2}+4x+5\) kwanza kutumia mali kama tulivyofanya katika sehemu ya mwisho na kisha grafu kwa kutumia mabadiliko. Ni njia gani unayopendelea? Kwa nini?
    2. Graph kazi ya quadratic\(f(x)=2x^{2}−4x−3\) kwanza kutumia mali kama tulivyofanya katika sehemu ya mwisho na kisha grafu kwa kutumia mabadiliko. Ni njia gani unayopendelea? Kwa nini?
    Jibu

    1. Majibu yanaweza kutofautiana.

    Self Check

    Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

    Takwimu hii ni orodha ya kutathmini ufahamu wako wa dhana zilizowasilishwa katika sehemu hii. ina 4 nguzo kinachoitwa I canâ € |, kujiamini, Pamoja na baadhi ya msaada, na No-I donâ €™ t kupata! Chini mimi canâ € |, kuna grafu Quadratic Kazi ya fomu f ya x sawa x squared pamoja k; grafu Quadratic Kazi ya fomu f ya x sawa na wingi x bala h squared; grafu kazi Quadratic ya fomu f ya x sawa mara x squared; grafu Quadratic Kazi Kutumia Ubadilishaji; kupata Kazi ya Quadratic kutoka Grafu yake. Nguzo nyingine zimeachwa tupu ili uangalie uelewa.
    Kielelezo 9.7.109

    b Baada ya kuangalia orodha, unafikiri umeandaliwa vizuri kwa sehemu inayofuata? Kwa nini au kwa nini?