Skip to main content
Global

9.9: Kutatua Ukosefu wa Quadratic

  1. Last updated
  2. Save as PDF
  • Page ID
    176443

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kutatua usawa quadratic graphically
    • Kutatua usawa quadratic algebraically

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kutatua:\(2x−3=0\).
      Ikiwa umekosa tatizo hili, kagua Mfano 2.2.
    2. Kutatua:\(2y^{2}+y=15\).
      Kama amekosa tatizo hili, mapitio Mfano 6.45.
    3. Tatua\(\frac{1}{x^{2}+2 x-8}>0\)
      Ikiwa umekosa tatizo hili, tathmini Mfano 7.56.

    Tumejifunza jinsi ya kutatua usawa wa mstari na usawa wa busara hapo awali. Baadhi ya mbinu tulizotumia kuzitatua zilikuwa sawa na baadhi zilikuwa tofauti. Sasa tutajifunza kutatua usawa ambao una kujieleza kwa quadratic. Tutatumia baadhi ya mbinu kutoka kutatua usawa wa mstari na wa busara pamoja na usawa wa quadratic. Sisi kutatua usawa quadratic njia mbili-wote graphically na algebraically.

    Kutatua Quadratic usawa Graphically

    equation quadratic ni katika hali ya kiwango wakati imeandikwa kama\(ax^{2}+bx+c=0\). Ikiwa tunachukua nafasi ya ishara sawa na ishara ya kutofautiana, tuna usawa wa quadratic katika fomu ya kawaida.

    Ufafanuzi\(\PageIndex{1}\): Quadratic Inequality

    Ukosefu wa usawa wa quadratic ni usawa ambao una kujieleza kwa quadratic. Aina ya kawaida ya usawa wa quadratic imeandikwa:

    \(\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}\)

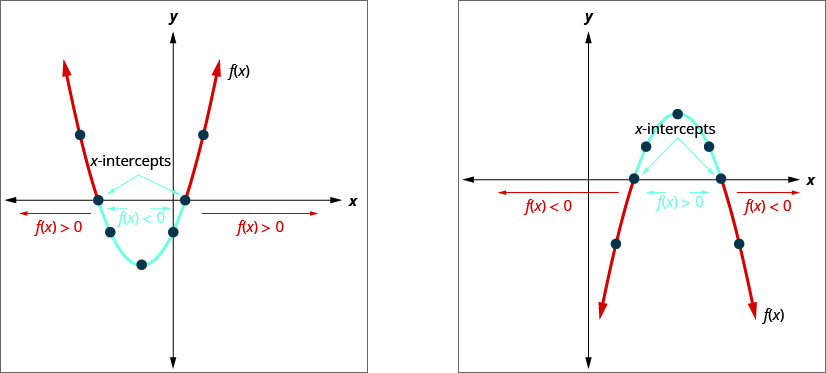
    Grafu ya kazi ya quadratic\(f(x)=a x^{2}+b x+c=0\) ni parabola. Wakati sisi kuuliza wakati ni\(a x^{2}+b x+c<0\), sisi ni kuuliza lini ni\(f(x)<0\). Tunataka kujua wakati parabola iko chini ya\(x\) -axis.

    Wakati sisi kuuliza wakati ni\(a x^{2}+b x+c>0\), sisi ni kuuliza lini ni\(f(x)>0\). Tunataka kujua wakati parabola iko juu ya\(y\) -axis.

    Grafu ya kwanza ni juu inakabiliwa na parabola, f ya x, kwenye ndege ya kuratibu y x. Kwa upande wa kushoto wa kazi, f ya x ni kubwa kuliko 0. Kati ya x-intercepts, f ya x ni chini ya 0. Kwa haki ya kazi, f ya x ni kubwa kuliko 0. Grafu ya pili ni parabola inayoelekea chini, f ya x, kwenye ndege ya kuratibu x y. Kwa upande wa kushoto wa kazi, f ya x ni chini ya 0. Kati ya x-intercepts, f ya x ni kubwa kuliko 0. Kwa haki ya kazi, f ya x ni chini ya 0.
    Kielelezo 9.8.1
    Mfano\(\PageIndex{1}\): How to Solve a Quadratic Inequality Graphically

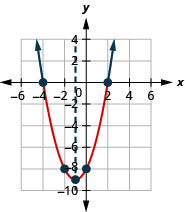
    Tatua\(x^{2}−6x+8<0\) graphically. Andika suluhisho katika maelezo ya muda.

    Suluhisho:

    Hatua ya 1: Andika usawa wa quadratic katika fomu ya kawaida.

    Ukosefu wa usawa ni katika fomu ya kawaida.

    \(x^{2}-6 x+8<0\)

    Hatua ya 2: Graph kazi\(f(x)=a x^{2}+b x+c\) kwa kutumia mali au mabadiliko.

    Sisi grafu kutumia mali.

    \(f(x)=x^{2}-6 x+8\)

    Angalia\(a\) katika equation.

    \(\color{red}{a=1, b=-6, c=8}\)

    \(f(x)=x^{2}-6 x+8\)

    Kwa kuwa\(a\) ni chanya, parabola inafungua juu.

    Parabola inafungua juu.

    Picha ya skrini (2) .png
    Kielelezo 9.8.2

    \(f(x)=x^{2}-6 x+8\)

    Mhimili wa ulinganifu ni mstari\(x=-\frac{b}{2 a}\).

    Axis ya Ulinganifu

    \(x=-\frac{b}{2 a}\)

    \(\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}\)

    Mhimili wa ulinganifu ni mstari\(x=3\).

    Vertex iko kwenye mhimili wa ulinganifu. Mbadala\(x=3\) katika kazi.

    Vertex

    \(\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}\)

    Vertex ni\((3,-1)\).

    Tunapata\(f(0)\)

    \(y\)-kukatiza

    \(\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}\)

    \(y\)Kizuizi ni\((0.8)\).

    Tunatumia mhimili wa ulinganifu ili kupata uhakika ulinganifu kwa\(y\) -intercept. \(y\)-Intercept ni\(3\) vitengo vya kushoto vya mhimili wa ulinganifu,\(x=3\). \(3\)vitengo uhakika na haki ya mhimili wa ulinganifu ina\(x=6\).

    Point ulinganifu kwa\(y\) -intercept

    Hatua ni\((6,8)\).

    Sisi kutatua\(f(x)=0\).

    \(x\)-hukataa

    Tunaweza kutatua equation hii quadratic kwa factoring.

    \(\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}\)

    \(x\)-intercepts ni\((2,0)\) na\((4,0)\).

    Sisi grafu vertex, intercepts, na uhakika ulinganifu kwa\(y\) -intercept. Tunaunganisha\(5\) pointi hizi ili mchoro wa parabola.

    Picha ya skrini (3) .png
    Kielelezo 9.8.3

    Hatua ya 3: Tambua suluhisho kutoka kwenye grafu.

    \(x^{2}-6 x+8<0\)

    Ukosefu wa usawa unauliza maadili\(x\) ambayo hufanya kazi chini ya\(0\). Ni maadili gani ya\(x\) kufanya parabola chini ya\(x\) -axis.

    Hatujumuishi maadili\(2\),\(4\) kama usawa ni chini ya tu.

    Suluhisho, katika maelezo ya muda, ni\((2,4)\).

    Zoezi\(\PageIndex{1}\)
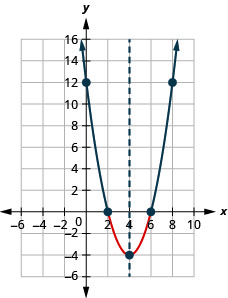
    1. Tatua\(x^{2}+2 x-8<0\) kielelezo
    2. Andika suluhisho katika maelezo ya muda
    Jibu

    1. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina kipeo cha (hasi 2, hasi 9), y-intercept ya (0, 8), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na hasi 2.
      Kielelezo 9.8.4
    2. \((-4,2)\)
    Zoezi\(\PageIndex{2}\)
    1. Tatua\(x^{2}-8 x+12 \geq 0\) kielelezo
    2. Andika suluhisho katika maelezo ya muda
    Jibu

    1. Takwimu hii inaonyesha parabola ya juu ya kufungua kwenye ndege ya kuratibu x y. Ina vertex ya (4, hasi 4) na x-intercepts ya (2, 0) na (6, 0).
      Kielelezo 9.8.5
    2. \((-\infty, 2] \cup[6, \infty)\)

    Tunaorodhesha hatua za kuchukua ili kutatua usawa wa quadratic graphically.

    Kutatua Usawa Quadratic Graphically

    1. Andika usawa wa quadratic katika fomu ya kawaida.
    2. Graph kazi\(f(x)=ax^{2}+bx+c\).
    3. Tambua suluhisho kutoka kwenye grafu.

    Katika mfano wa mwisho, parabola ilifunguliwa juu na katika mfano unaofuata, inafungua chini. Katika matukio hayo yote, tunatafuta sehemu ya parabola iliyo chini ya\(x\) -axis lakini angalia jinsi msimamo wa parabola huathiri suluhisho.

    Mfano\(\PageIndex{2}\)

    Tatua\(-x^{2}-8 x-12 \leq 0\) graphically. Andika suluhisho katika maelezo ya muda.

    Suluhisho:

    Ukosefu wa usawa wa quadratic katika fomu ya kawaida. \(-x^{2}-8 x-12 \leq 0\)

    Graph kazi

    \(f(x)=-x^{2}-8 x-12\)

    Parabola inafungua chini.

    .
    Kielelezo 9.8.6
    Pata mstari wa ulinganifu. \(\begin{array}{l}{x=-\frac{b}{2 a}} \\ {x=-\frac{-8}{2(-1)}} \\ {x=-4}\end{array}\)
    Pata vertex.

    \(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ f(-4) &=-(-4)^{2}-8(-4)-12 \\ f(-4) &=-16+32-12 \\ & f(-4)=4 \end{aligned}\)

    Vertex\((-4,4)\)
    Kupata\(x\) -intercepts. Hebu\(f(x)=0\). \(\begin{aligned} f(x) &=-x^{2}-8 x-12 \\ 0 &=-x^{2}-8 x-12 \end{aligned}\)
    sababu: Matumizi Zero Bidhaa Mali. \(\begin{array}{l}{0=-1(x+6)(x+2)} \\ {x=-6 \quad x=-2}\end{array}\)
    Grafu parabola.

    \(x\)-hukataa\((-6,0), (-2.0)\)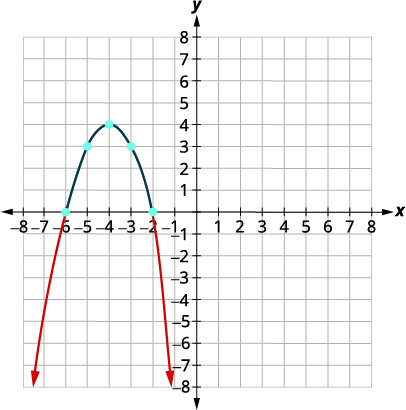

    .
    Kielelezo 9.8.7
    Tambua suluhisho kutoka kwenye grafu. Sisi ni pamoja na\(x\) -intercepts kama kukosekana kwa usawa ni “chini ya au sawa na.” \((-\infty,-6] \cup[-2, \infty)\)
    Jedwali 9.8.1
    Zoezi\(\PageIndex{3}\)
    1. Tatua\(-x^{2}-6 x-5>0\) kielelezo
    2. Andika suluhisho katika maelezo ya muda
    Jibu

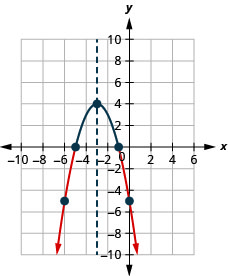
    1. parabola chini-inakabiliwa na juu ya x y-kuratibu ndege. Ina kipeo cha (hasi 3, 4), y-intercept saa (0, hasi 5), na mhimili wa ulinganifu umeonyeshwa kwenye x sawa na hasi 3.
      Kielelezo 9.8.8
    2. \((-5,-1)\)
    Zoezi\(\PageIndex{4}\)
    1. Tatua\(−x^{2}+10x−16≤0\) kielelezo
    2. Andika suluhisho katika maelezo ya muda
    Jibu

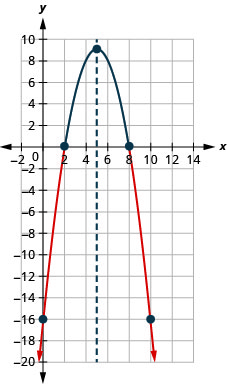
    1. parabola chini-inakabiliwa na juu ya x y-kuratibu ndege. Ina kipeo cha (5, 9), y-intercept saa (0, hasi 16), na mhimili wa ulinganifu wa x sawa na 5.
      Kielelezo 9.8.9
    2. \((-\infty, 2] \cup[8, \infty)\)

    Kutatua Usawa Quadratic Algebraically

    Njia ya algebraic tutakayotumia ni sawa na njia tuliyotumia kutatua usawa wa busara. Tutapata pointi muhimu kwa usawa, ambayo itakuwa ufumbuzi wa equation ya quadratic inayohusiana. Kumbuka maneno ya polynomial yanaweza kubadilisha ishara tu ambapo maneno ni sifuri.

    Tutatumia pointi muhimu kugawanya mstari wa nambari katika vipindi na kisha kuamua kama kujieleza kwa quadratic itakuwa chanya au hasi kwa muda. Sisi kisha kuamua ufumbuzi kwa ajili ya kukosekana kwa usawa.

    Mfano\(\PageIndex{3}\): How to Solve Quadratic Inequalities Algebraically

    Kutatua\(x^{2}-x-12 \geq 0\) algebraically. Andika suluhisho katika maelezo ya muda.

    Suluhisho:

    Hatua ya 1: Andika usawa wa quadratic katika fomu ya kawaida. Ukosefu wa usawa ni katika fomu ya kawaida. \(x^{2}-x-12 \geq 0\)
    Hatua ya 2: Tambua pointi muhimu-ufumbuzi wa equation ya quadratic inayohusiana. Badilisha ishara ya usawa kwa ishara sawa na kisha kutatua equation. \(\begin{array}{c}{x^{2}-x-12=0} \\ {(x+3)(x-4)=0} \\ {x+3=0 \quad x-4=0} \\ {x=-3 \quad x=4}\end{array}\)
    Hatua ya 3: Tumia pointi muhimu kugawanya mstari wa nambari katika vipindi. Tumia\(-3\) na\(4\) kugawanya mstari wa nambari katika vipindi. 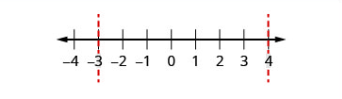Picha ya skrini (4) .png
    Hatua ya 4: Juu ya mstari wa nambari onyesha ishara ya kila kujieleza quadratic kwa kutumia pointi za mtihani kutoka kila kipindi kilichobadilishwa kutoka usawa wa awali.

    Mtihani:

    \(x=-5\)

    \(x=0\)

    \(x=5\)

    \(\begin{array}{ccc}{x^{2}-x-12} & {x^{2}-x-12} & {x^{2}-x-12} \\ {(-5)^{2}-(-5)-12} & {0^{2}-0-12} & {5^{2}-5-12} \\ {18} & {-12} & {8}\end{array}\)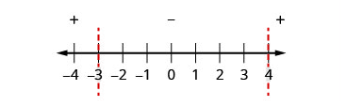

    Picha ya skrini (5) .png
    Kielelezo 9.8.11
    Hatua ya 5: Tambua vipindi ambapo usawa ni sahihi. Andika suluhisho katika maelezo ya muda.

    \(x^{2}-x-12 \geq 0\)

    Ukosefu wa usawa ni chanya katika vipindi vya kwanza na vya mwisho na ni sawa\(0\) na pointi\(-4,3\).

    		 Suluhisho, katika maelezo ya muda, ni\((-\infty,-3] \cup[4, \infty)\).
    Jedwali 9.8.2
    Zoezi\(\PageIndex{5}\)

    Kutatua\(x^{2}+2x−8≥0\) algebraically. Andika suluhisho katika maelezo ya muda.

    Jibu

    \((-\infty,-4] \cup[2, \infty)\)

    Zoezi\(\PageIndex{6}\)

    Kutatua\(x^{2}−2x−15≤0\) algebraically. Andika suluhisho katika maelezo ya muda.

    Jibu

    \([-3,5]\)

    Katika mfano huu, kwa\(x^{2}−x−12\) sababu ya kujieleza vizuri, tunaweza pia kupata ishara katika kila kipindi kiasi kama tulivyofanya wakati sisi kutatuliwa usawa busara. Tunapata ishara ya kila sababu, na kisha ishara ya bidhaa. Nambari yetu ya mstari ungependa hii:

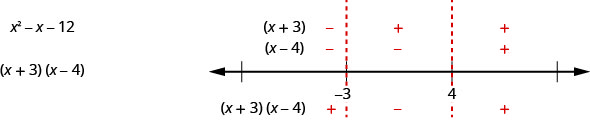
    Takwimu inaonyesha maneno x squared minus x minus 12 factored kwa wingi wa x pamoja na mara 3 kiasi cha x minus 4. Picha inaonyesha mstari wa nambari unaoonyesha mistari ya dotted kwenye hasi 3 na 4. Inaonyesha ishara za wingi x pamoja na 3 kuwa hasi, chanya, chanya, na ishara za kiasi x minus 4 kuwa hasi, hasi, chanya. Chini ya mstari wa nambari, inaonyesha kiasi x pamoja na mara 3 kiasi x minus 4 na ishara chanya, hasi, chanya.
    Kielelezo 9.8.12

    Matokeo yake ni sawa na tulivyopata kutumia njia nyingine.

    Sisi muhtasari hatua hapa.

    Kutatua Usawa Quadratic Algebraically

    1. Andika usawa wa quadratic katika fomu ya kawaida.
    2. Kuamua pointi muhimu-ufumbuzi wa equation kuhusiana quadratic.
    3. Tumia pointi muhimu kugawanya mstari wa nambari katika vipindi.
    4. Juu ya mstari wa nambari onyesha ishara ya kila kujieleza quadratic kwa kutumia pointi za mtihani kutoka kila kipindi kilichobadilishwa kuwa usawa wa awali.
    5. Kuamua vipindi ambapo usawa ni sahihi. Andika suluhisho katika maelezo ya muda.
    Mfano\(\PageIndex{4}\)

    Kutatua\(x^{2}+6x−7≥0\) algebraically. Andika suluhisho katika maelezo ya muda.

    Suluhisho:

    Andika usawa wa quadratic katika fomu ya kawaida. \(-x^{2}+6 x-7 \geq 0\)
    Kuzidisha pande zote mbili za kukosekana kwa usawa na\(-1\). Kumbuka kubadili ishara ya usawa. \(x^{2}-6 x+7 \leq 0\)
    Kuamua pointi muhimu kwa kutatua equation kuhusiana quadratic. \(x^{2}-6 x+7=0\)
    Andika Mfumo wa Quadratic. \(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
    Kisha mbadala katika maadili ya\(a, b, c\). \(x=\frac{-(-6) \pm \sqrt{(-6)^{2}-4 \cdot 1 \cdot(7)}}{2 \cdot 1}\)
    Kurahisisha. \(x=\frac{6 \pm \sqrt{8}}{2}\)
    Kurahisisha radical. \(x=\frac{6 \pm 2 \sqrt{2}}{2}\)
    Ondoa jambo la kawaida,\(2\). \(\begin{array}{l}{x=\frac{2(3 \pm \sqrt{2})}{2}} \\ {x=3 \pm \sqrt{2}} \\ {x=3+\sqrt{2}} \quad x=3-\sqrt{2} \\ {x \approx 1.6}\quad\quad\:\:\: x\approx 4.4\end{array}\)
    Tumia pointi muhimu kugawanya mstari wa nambari katika vipindi. Nambari za mtihani kutoka kila kipindi katika usawa wa awali. .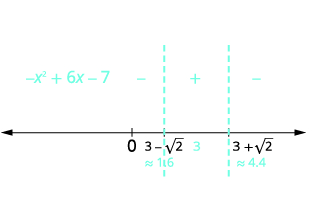
    Kuamua vipindi ambapo usawa ni sahihi. Andika suluhisho katika maelezo ya muda. \(-x^{2}+6 x-7 \geq 0\)katika kipindi cha kati\([3-\sqrt{2}, 3+\sqrt{2}]\)
    Jedwali 9.8.3
    Zoezi\(\PageIndex{7}\)

    Kutatua\(−x^{2}+2x+1≥0\) algebraically. Andika suluhisho katika maelezo ya muda.

    Jibu

    \([-1-\sqrt{2},-1+\sqrt{2}]\)

    Zoezi\(\PageIndex{8}\)

    Kutatua\(−x^{2}+8x−14<0\) algebraically. Andika suluhisho katika maelezo ya muda.

    Jibu

    \((-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)\)

    Ufumbuzi wa kutofautiana kwa quadratic katika kila moja ya mifano ya awali, ilikuwa ama muda au umoja wa vipindi viwili. Hii ilisababisha ukweli kwamba, katika kila kesi tulipata ufumbuzi mbili kwa equation sambamba quadratic\(ax^{2}+bx+c=0\). Ufumbuzi huu wawili basi alitupa ama mbili\(x\) - intercepts kwa grafu au pointi mbili muhimu kugawanya mstari namba katika vipindi.

    Hii inahusiana na majadiliano yetu ya awali ya idadi na aina ya ufumbuzi wa equation quadratic kutumia ubaguzi.

    Kwa equation quadratic ya fomu\(ax^{2}+bc+c=0, a≠0\).

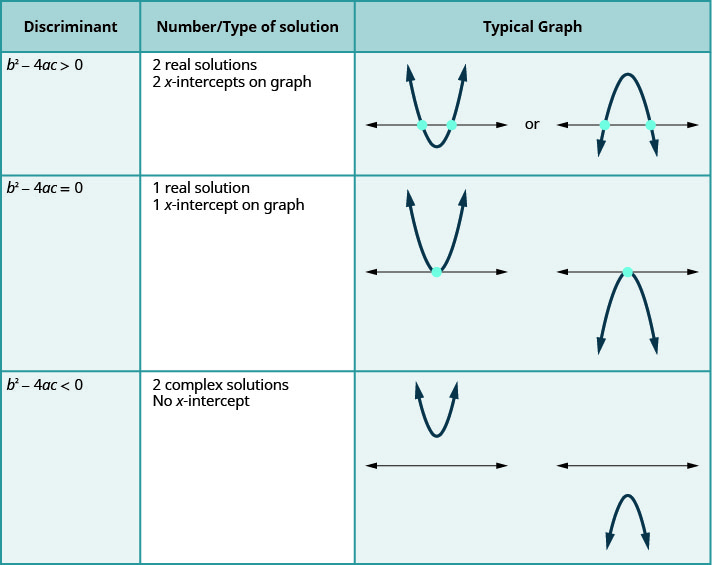
    Takwimu ni meza yenye nguzo 3. Safu ya 1 imeandikwa ubaguzi, safu ya 2 ni Idadi/Aina ya suluhisho, na safu ya 3 ni Grafu ya kawaida. Kusoma kwenye nguzo, ikiwa b squared minus mara 4 kwa mara c ni kubwa kuliko 0, kutakuwa na 2 ufumbuzi halisi kwa sababu kuna 2 x-intercepts kwenye grafu. Picha ya grafu ya kawaida ni parabola ya juu au ya chini na 2 x-intercepts. Ikiwa ubaguzi b squared minus mara 4 kwa mara c ni sawa na 0, basi kuna 1 ufumbuzi halisi kwa sababu kuna 1 x-intercept kwenye grafu. Picha ya grafu ya kawaida ni parabola ya juu au ya chini-inayoelekea ambayo ina vertex kwenye mhimili wa x-badala ya kuvuka. Ikiwa ubaguzi b squared minus mara 4 mara c ni chini ya 0, kuna 2 ufumbuzi tata kwa sababu hakuna x-intercept. Picha ya grafu ya kawaida inaonyesha parabola ya juu au ya chini-inayoelekea ambayo haina msalaba wa x-axis.
    Kielelezo 9.8.14

    Mstari wa mwisho wa meza unatuonyesha wakati parabolas hazipatikani kamwe\(x\) -axis. Kutumia Mfumo wa Quadratic kutatua equation quadratic, radicand ni hasi. Tunapata ufumbuzi wawili tata.

    Katika mfano unaofuata, ufumbuzi wa usawa wa quadratic utatokana na suluhisho la equation ya quadratic kuwa ngumu.

    Mfano\(\PageIndex{5}\)

    Tatua, kuandika suluhisho lolote katika maelezo ya muda:

    1. \(x^{2}-3 x+4>0\)
    2. \(x^{2}-3 x+4 \leq 0\)

    Suluhisho:

    a.

    Andika usawa wa quadratic katika fomu ya kawaida. \(-x^{2}-3 x+4>0\)
    Kuamua pointi muhimu kwa kutatua equation kuhusiana quadratic. \(x^{2}-3 x+4=0\)
    Andika Mfumo wa Quadratic. \(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
    Kisha mbadala katika maadili ya\(a, b, c\). \(x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \cdot 1 \cdot(4)}}{2 \cdot 1}\)
    Kurahisisha. \(x=\frac{3 \pm \sqrt{-7}}{2}\)
    Kurahisisha radicand. \(x=\frac{3 \pm \sqrt{7 i}}{2}\)
    Ufumbuzi tata unatuambia
    parabola haina kuzuia\(x\) -axis.
    Pia, parabola inafungua juu. Hii
    inatuambia kwamba parabola iko kabisa juu ya\(x\) -axis.

    Ufumbuzi tata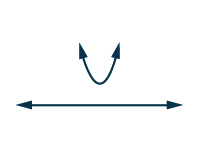

    .
    Kielelezo 9.8.15
    Jedwali 9.8.4

    Sisi ni kupata ufumbuzi wa\(x^{2}−3x+4>0\). Tangu kwa maadili yote\(x\) ya grafu ni juu ya\(x\) -axis, maadili yote ya\(x\) kufanya usawa wa kweli. Katika notation ya muda tunaandika\((−∞,∞)\).

    b Andika usawa wa quadratic katika fomu ya kawaida.

    \(x^{2}-3 x+4 \leq 0\)

    Kuamua pointi muhimu kwa kutatua equation kuhusiana quadratic.

    \(x^{2}-3 x+4=0\)

    Kwa kuwa equation sambamba quadratic ni sawa na katika sehemu (a), parabola itakuwa sawa. Parabola inafungua juu na iko kabisa juu ya\(x\) -axis-hakuna sehemu yake iko chini ya\(x\) -axis.

    Sisi ni kupata ufumbuzi wa\(x^{2}−3x+4≤0\). Tangu kwa maadili yote\(x\) ya grafu ni kamwe chini ya\(x\) -axis, hakuna maadili ya\(x\) kufanya usawa kweli. Hakuna ufumbuzi wa kukosekana kwa usawa.

    Zoezi\(\PageIndex{9}\)

    Tatua na uandike suluhisho lolote katika maelezo ya muda:

    1. \(-x^{2}+2 x-4 \leq 0\)
    2. \(-x^{2}+2 x-4 \geq 0\)
    Jibu
    1. \((-\infty, \infty)\)
    2. hakuna suluhisho
    Zoezi\(\PageIndex{10}\)

    Tatua na uandike suluhisho lolote katika maelezo ya muda:

    1. \(x^{2}+3 x+3<0\)
    2. \(x^{2}+3 x+3>0\)
    Jibu
    1. hakuna suluhisho
    2. \((-\infty, \infty)\)

    Dhana muhimu

    • Kutatua Usawa Quadratic Graphically
      1. Andika usawa wa quadratic katika fomu ya kawaida.
      2. Graph kazi\(f(x)=ax^{2}+bx+c\) kwa kutumia mali au mabadiliko.
      3. Tambua suluhisho kutoka kwenye grafu.
    • Jinsi ya Kutatua Ukosefu wa Quadratic Algebraically
      1. Andika usawa wa quadratic katika fomu ya kawaida.
      2. Kuamua pointi muhimu — ufumbuzi wa equation kuhusiana quadratic.
      3. Tumia pointi muhimu kugawanya mstari wa nambari katika vipindi.
      4. Juu ya mstari wa nambari onyesha ishara ya kila kujieleza quadratic kwa kutumia pointi za mtihani kutoka kila kipindi kilichobadilishwa kuwa usawa wa awali.
      5. Kuamua vipindi ambapo usawa ni sahihi. Andika suluhisho katika maelezo ya muda.

    faharasa

    quadratic usawa
    Ukosefu wa usawa wa quadratic ni usawa ambao una kujieleza kwa quadratic.