Skip to main content
Global

9.8: Kazi za Quadratic za Grafu Kutumia Mabadiliko

  1. Last updated
  2. Save as PDF
  • Page ID
    176477

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Graph quadratic kazi ya fomu\(f(x)=x^{2}+k\)
    • Graph quadratic kazi ya fomu\(f(x)=(x−h)^{2}\)
    • Graph quadratic kazi ya fomu\(f(x)=ax^{2}\)
    • Grafu quadratic kazi kwa kutumia mabadiliko
    • Pata kazi ya quadratic kutoka kwenye grafu yake

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Graph kazi\(f(x)=x^{2}\) kwa pointi za kupanga.
      Kama amekosa tatizo hili, mapitio Mfano 3.54.
    2. Sababu kabisa:\(y^{2}−14y+49\).
      Kama amekosa tatizo hili, mapitio Mfano 6.24.
    3. Sababu kabisa:\(2x^{2}−16x+32\).
      Kama amekosa tatizo hili, mapitio Mfano 6.26.

    Grafu Quadratic Kazi ya Fomu\(f(x)=x^{2}+k\)

    Katika sehemu ya mwisho, tulijifunza jinsi ya kuchora kazi za quadratic kwa kutumia mali zao. Njia nyingine inahusisha kuanzia na grafu ya msingi ya\(f(x)=x^{2}\) na 'kusonga' kulingana na taarifa iliyotolewa katika equation ya kazi. Tunaita kazi hii ya quadratic ya graphing kwa kutumia mabadiliko.

    Katika mfano wa kwanza, tutaweka kazi ya quadratic\(f(x)=x^{2}\) kwa pointi za kupanga njama. Kisha tutaona nini athari kuongeza mara kwa mara,\(k\), kwa equation itakuwa na juu ya grafu ya kazi mpya\(f(x)=x^{2}+k\).

    Mfano\(\PageIndex{1}\)

    Grafu\(f(x)=x^{2}\),\(g(x)=x^{2}+2\), na\(h(x)=x^{2}−2\) kwenye mfumo huo wa kuratibu mstatili. Eleza nini athari kuongeza mara kwa mara kwa kazi ina juu ya parabola msingi.

    Suluhisho:

    Vipengele vya kupanga vitatusaidia kuona athari za vipindi kwenye\(f(x)=x^{2}\) grafu ya msingi. Tunajaza chati kwa kazi zote tatu.

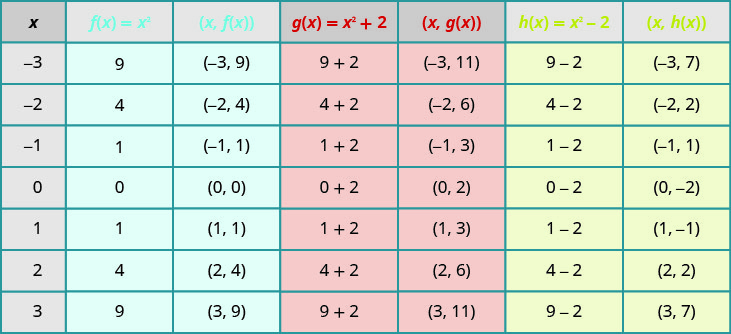
    Jedwali inayoonyesha athari za mara kwa mara kwenye kazi ya msingi ya x squared. Jedwali lina nguzo saba zilizoandikwa x, f ya x sawa x squared, jozi iliyoamriwa (x, f ya x), g ya x sawa x squared plus 2, jozi iliyoamuru (x, g ya x), h ya x sawa x squared bala 2, na jozi iliyoamriwa (x, h ya x). Katika safu ya x, maadili yaliyotolewa ni hasi 3, hasi 2, hasi 1, 0, 1, 2, na 3. Katika f ya x sawa x safu ya mraba, maadili ni 9, 4, 1, 0, 1, 4, na 9. Katika safu (x, f ya x), jozi zilizoamriwa (hasi 3, 9), (hasi 2, 4), (hasi 1, 1), (0, 0), (1, 1), (2, 4), na (3, 9) hutolewa. g ya x sawa x mraba pamoja na safu ya 2 ina maneno 9 pamoja na 2, 4 pamoja na 2, 1 pamoja na 2, 0 pamoja na 2, 1 pamoja na 2, 4 pamoja na 2, na 9 pamoja na 2. Safu ya (x, g ya x) ina jozi zilizoamriwa za (hasi 3, 11), (hasi 2, 6), (hasi 1, 3), (0, 2), (1, 3), (2, 6), na (3, 11). Katika h ya x sawa x mraba minus 2 safu, maneno yaliyotolewa ni 9 minus 2, 4 minus 2, 1 minus 2, 0 minus 2, 1 minus 2, 4 minus 2, na 9 minus 2. Katika safu ya mwisho, (x, h ya x), ina jozi zilizoagizwa (hasi 3, 7), (hasi 2, 2), (hasi 1, hasi 1), (0, hasi 2), (1, hasi 1), (2, 2), na (3, 7).
    Kielelezo 9.7.1

    \(g(x)\)Maadili ni mbili zaidi kuliko\(f(x)\) maadili. Pia,\(h(x)\) maadili ni mawili chini ya\(f(x)\) maadili. Sasa tutaweka kazi zote tatu kwenye mfumo huo wa kuratibu mstatili.

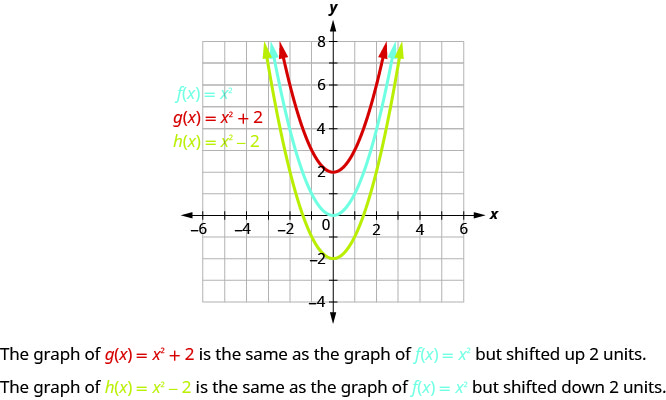
    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Katikati ni grafu ya f ya x sawa x squared ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Parabola ya juu imehamishwa hadi vitengo 2, na chini imehamishwa chini vitengo 2.
    Kielelezo 9.7.2

    Grafu ya\(g(x)=x^{2}+2\) ni sawa na grafu ya\(2\) vitengo\(f(x)=x^{2}\) lakini vilivyobadilishwa.

    Grafu ya\(h(x)=x^{2}−2\) ni sawa na grafu ya\(2\) vitengo\(f(x)=x^{2}\) lakini kubadilishwa chini.

    Zoezi\(\PageIndex{1}\)
    1. Grafu\(f(x)=x^{2}, g(x)=x^{2}+1,\) na\(h(x)=x^{2}-1\) kwenye mfumo huo wa kuratibu mstatili.
    2. Eleza nini athari kuongeza mara kwa mara kwa kazi ina juu ya parabola msingi.
    Jibu

    a.

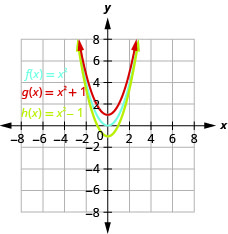
    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Grafu ya kati ni ya f ya x sawa x mraba ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve juu imekuwa wakiongozwa hadi 1 kitengo, na chini imekuwa wakiongozwa chini 1 kitengo.
    Kielelezo 9.7.3

    b. grafu ya\(g(x)=x^{2}+1\) ni sawa na grafu ya\(f(x)=x^{2}\) lakini kubadilishwa up\(1\) kitengo. Grafu ya\(h(x)=x^{2}−1\) ni sawa na grafu ya\(f(x)=x^{2}\) lakini imebadilishwa\(1\) kitengo.

    Zoezi\(\PageIndex{2}\)
    1. Grafu\(f(x)=x^{2}, g(x)=x^{2}+6,\) na\(h(x)=x^{2}-6\) kwenye mfumo huo wa kuratibu mstatili.
    2. Eleza nini athari kuongeza mara kwa mara kwa kazi ina juu ya parabola msingi.
    Jibu

    a.

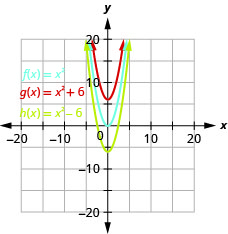
    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve katikati ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve juu imekuwa wakiongozwa hadi 6 vitengo, na chini imekuwa wakiongozwa chini 6 vitengo.
    Kielelezo 9.7.4

    b. grafu ya\(h(x)=x^{2}+6\) ni sawa na grafu ya\(f(x)=x^{2}\) lakini kubadilishwa up\(6\) vitengo. Grafu ya\(h(x)=x^{2}-6\) ni sawa na grafu ya\(6\) vitengo\(f(x)=x^{2}\) lakini kubadilishwa chini.

    Mfano wa mwisho unaonyesha kwamba kwa grafu ya kazi ya quadratic ya fomu\(f(x)=x^{2}+k\), tunachukua grafu ya msingi ya parabola\(f(x)=x^{2}\) na kuibadilisha kwa wima\((k>0)\) au kuibadilisha\((k<0)\).

    Mabadiliko haya inaitwa mabadiliko ya wima.

    Grafu Kazi ya Quadratic ya Fomu\(f(x)=x^{2}+k\) Kutumia Shift ya Wima

    Grafu ya\(f(x)=x^{2}+k\) mabadiliko grafu ya\(k\) vitengo vya\(f(x)=x^{2}\) wima.

    • Kama\(k>0\), kuhama parabola wima up\(k\) vitengo.
    • Kama\(k<0\), kuhama parabola wima chini\(|k|\) vitengo.

    Sasa kwa kuwa tumeona athari za mara kwa mara\(k\), ni rahisi kwa graph kazi ya fomu\(f(x)=x^{2}+k\). Sisi tu kuanza na parabola ya msingi ya\(f(x)=x^{2}\) na kisha kuhama juu au chini.

    Inaweza kuwa na manufaa kwa mazoezi sketching\(f(x)=x^{2}\) haraka. Tunajua maadili na tunaweza kuchora grafu kutoka huko.

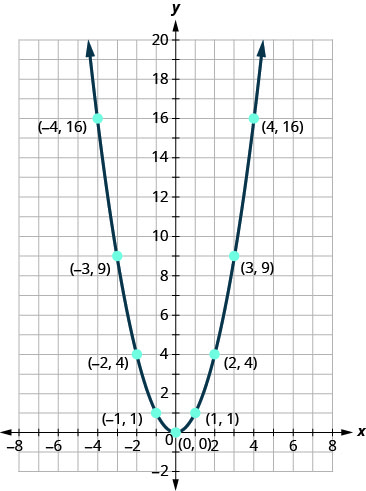
    Takwimu hii inaonyesha parabola ya juu-kufungua kwenye ndege ya kuratibu x y, na kipeo (0, 0). Vipengele vingine kwenye safu ziko kwenye (hasi 4, 16), (hasi 3, 9), (hasi 2, 4), (hasi 1, 1), (1, 1), (2, 4), (3, 9), na (4, 16).
    Kielelezo 9.7.5

    Mara tu tunajua parabola hii, itakuwa rahisi kutumia mabadiliko. Mfano unaofuata utahitaji mabadiliko ya wima.

    Mfano\(\PageIndex{2}\)

    Grafu\(f(x)=x^{2}−3\) kutumia mabadiliko ya wima.

    Suluhisho:

    Sisi kwanza kuteka grafu ya grafu ya\(f(x)=x^{2}\) gridi ya taifa. 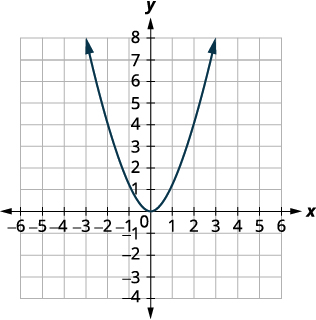Takwimu hii inaonyesha parabola ya juu-kufungua kwenye ndege ya kuratibu x y na kipeo cha (0, 0) na pointi nyingine kwenye safu iliyoko (hasi 1, 1) na (1, 1). Ni grafu ya f ya x sawa x squared.
    Kuamua\(k\). .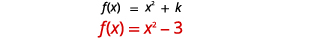
      .
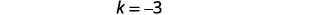    Shift grafu\(f(x)=x^{2}\) chini\(3\). 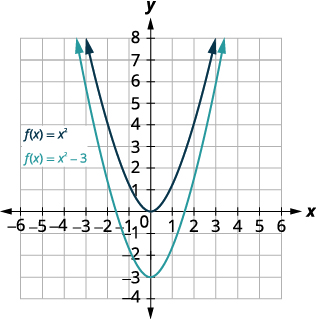Takwimu hii inaonyesha 2 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve juu ni grafu ya f ya x sawa x squared ambayo ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve ya chini imehamishwa chini vitengo 3.
    Jedwali 9.7.1
    Zoezi\(\PageIndex{3}\)

    Grafu\(f(x)=x^{2}−5\) kutumia mabadiliko ya wima.

    Jibu
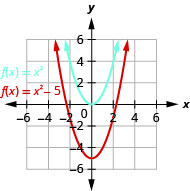
    Takwimu hii inaonyesha 2 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve juu ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve ya chini imehamishwa chini vitengo 5.
    Kielelezo 9.7.10
    Zoezi\(\PageIndex{4}\)

    Grafu\(f(x)=x^{2}+7\) kutumia mabadiliko ya wima.

    Jibu
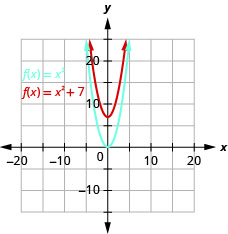
    Takwimu hii inaonyesha 2 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve chini ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve juu imekuwa wakiongozwa hadi 7 vitengo.
    Kielelezo 9.7.11

    Grafu Quadratic Kazi ya Fomu\(f(x)=(x-h)^{2}\)

    Katika mfano wa kwanza, tulipiga kazi ya quadratic\(f(x)=x^{2}\) kwa pointi za kupanga njama na kisha tukaona athari ya kuongeza mara\(k\) kwa mara kwa kazi iliyo kwenye grafu inayosababisha kazi mpya\(f(x)=x^{2}+k\).

    Sisi sasa kuchunguza athari za kutoa mara kwa mara\(h\), kutoka\(x\) ina juu ya grafu kusababisha ya kazi mpya\(f(x)=(x−h)^{2}\).

    Mfano\(\PageIndex{3}\)

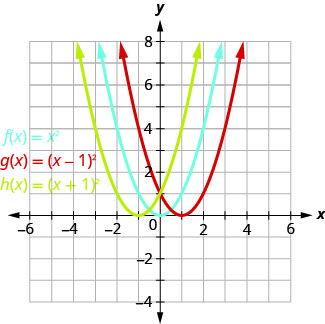
    Grafu\(f(x)=x^{2}, g(x)=(x-1)^{2},\) na\(h(x)=(x+1)^{2}\) kwenye mfumo huo wa kuratibu mstatili. Eleza nini athari kuongeza mara kwa mara kwa kazi ina juu ya parabola msingi.

    Suluhisho:

    Vipengele vya kupanga vitatusaidia kuona athari za vipindi kwenye\(f(x)=x^{2}\) grafu ya msingi. Tunajaza chati kwa kazi zote tatu.

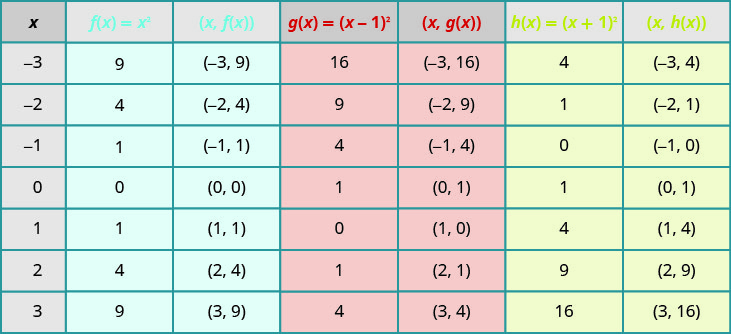
    Jedwali inayoonyesha athari za mara kwa mara kwenye kazi ya msingi ya x squared. Jedwali lina nguzo saba zilizoandikwa x, f ya x sawa x squared, jozi iliyoamriwa (x, f ya x), g ya x sawa na kiasi cha x bala 1 mraba, jozi iliyoamriwa (x, g ya x), h ya x sawa na wingi wa x plus 1 squared, na jozi iliyoamriwa (x, h ya x). Katika safu ya x, maadili yaliyotolewa ni hasi 3, hasi 2, hasi 1, 0, 1, 2, na 3. Katika f ya x sawa x safu ya mraba, maadili ni 9, 4, 1, 0, 1, 4, na 9. Katika safu (x, f ya x), jozi zilizoamriwa (hasi 3, 9), (hasi 2, 4), (hasi 1, 1), (0, 0), (1, 1), (2, 4), na (3, 9) hutolewa. g ya x ni sawa na kiasi cha x minus 1 safu ya mraba ina maadili ya 16, 9, 4, 1, 0, 1, na 4. Safu ya (x, g ya x) ina jozi zilizoamriwa za (hasi 3, 1), (hasi 2, 9), (hasi 1, 4), (0, 1), (2, 1), na (3, 4). Katika h ya x sawa na wingi wa x pamoja na 1 squared, maadili yaliyotolewa ni 4, 1, 0, 1, 4, 9, na 16. Katika safu ya mwisho, (x, h ya x), ina jozi zilizoagizwa (hasi 3, 4), (hasi 2, 1), (hasi 1, 0), (0, 4), (1, hasi 1), (2, 9), na (3, 16).
    Kielelezo 9.7.12

    \(g(x)\)Maadili na\(h(x)\) maadili hushiriki idadi ya kawaida\(0, 1, 4, 9\), na\(16\), lakini hubadilishwa.

    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve katikati ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve ya kushoto imehamishwa kwenye kitengo cha kushoto cha 1, na safu ya kulia imehamishwa kwenye kitengo cha 1 cha kulia.
    Kielelezo 9.7.13
    Takwimu inasema kwenye mstari wa kwanza kwamba grafu ya g ya x inalingana na kiasi x bala 1 mraba ni sawa na grafu ya f ya x sawa na x squared lakini kubadilishwa haki 1 kitengo. Mstari wa pili unasema kwamba grafu ya h ya x sawa na kiasi x pamoja na 1 mraba ni sawa na grafu ya f ya x sawa na x squared lakini kubadilishwa kushoto kitengo 1. Mstari wa tatu wa takwimu unasema g ya x sawa na kiasi x bala 1 mraba na mshale chini yake akielezea haki na kitengo 1 kilichoandikwa kando yake. Hatimaye, inatoa h ya x sawa na wingi wa x plus 1 squared na mshale chini yake akizungumzia upande wa kushoto na 1 kitengo imeandikwa kando yake.
    Kielelezo 9.7.14
    Zoezi\(\PageIndex{5}\)
    1. Grafu\(f(x)=x^{2}, g(x)=(x+2)^{2},\) na\(h(x)=(x-2)^{2}\) kwenye mfumo huo wa kuratibu mstatili.
    2. Eleza nini athari kuongeza mara kwa mara kwa kazi ina juu ya parabola msingi.
    Jibu

    a.

    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve katikati ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve ya kushoto imehamishwa kwenye vitengo vya kushoto vya 2, na safu ya kulia imehamishwa kwenye vitengo 2 vya kulia.
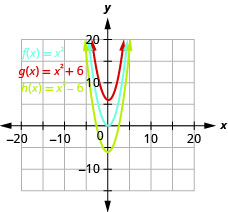
    Kielelezo 9.7.15

    b. grafu ya\(g(x)=(x+2)^{2}\) ni sawa na grafu ya\(2\) vitengo\(f(x)=x^{2}\) lakini kubadilishwa kushoto. Grafu ya\(h(x)=(x−2)^{2}\) ni sawa na grafu ya\(2\) vitengo\(f(x)=x^{2}\) lakini kuhama haki.

    Zoezi\(\PageIndex{6}\)
    1. Grafu\(f(x)=x^{2}, g(x)=x^{2}+5,\) na\(h(x)=x^{2}-5\) kwenye mfumo huo wa kuratibu mstatili.
    2. Eleza nini athari kuongeza mara kwa mara kwa kazi ina juu ya parabola msingi.
    Jibu

    a.

    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve katikati ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve ya kushoto imehamishwa kwenye vitengo vya kushoto vya 5, na safu ya kulia imehamishwa kwenye vitengo vya 5 vya kulia.
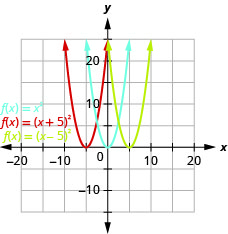
    Kielelezo 9.7.16

    b. grafu ya\(g(x)=(x+5)^{2}\) ni sawa na grafu ya\(5\) vitengo\(f(x)=x^{2}\) lakini kubadilishwa kushoto. Grafu ya\(h(x)=(x-5)^{2}\) ni sawa na grafu ya\(5\) vitengo vya haki\(f(x)=x^{2}\) lakini vilivyobadilishwa.

    Mfano wa mwisho unaonyesha kwamba kwa grafu ya kazi ya quadratic ya fomu\(f(x)=(x−h)^{2}\), tunachukua grafu ya msingi ya parabola\(f(x)=x^{2}\) na kuibadilisha kushoto\((h>0)\) au kuibadilisha haki\((h<0)\).

    Mabadiliko haya inaitwa mabadiliko ya usawa.

    Grafu Kazi ya Quadratic ya Fomu\(f(x)=(x-h)^{2}\) Kutumia Shift Horizontal

    Grafu ya\(f(x)=(x-h)^{2}\) mabadiliko grafu ya\(h\) vitengo vya\(f(x)=x^{2}\) usawa.

    • Kama\(h>0\), kuhama parabola usawa\(h\) vitengo kushoto.
    • Kama\(h<0\), kuhama parabola usawa\(|h|\) vitengo haki.

    Sasa kwa kuwa tumeona athari za mara kwa mara\(h\), ni rahisi kwa graph kazi ya fomu\(f(x)=(x−h)^{2}\). Sisi tu kuanza na parabola ya msingi ya\(f(x)=x^{2}\) na kisha kuhama ni kushoto au kulia.

    Mfano unaofuata utahitaji mabadiliko ya usawa.

    Mfano\(\PageIndex{4}\)

    Grafu\(f(x)=(x−6)^{2}\) kwa kutumia mabadiliko ya usawa.

    Suluhisho:

    Sisi kwanza kuteka grafu ya grafu ya\(f(x)=x^{2}\) gridi ya taifa. .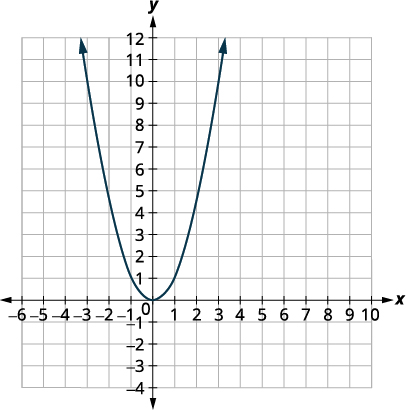
    Kuamua\(h\). .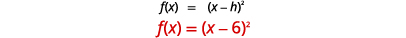
      .
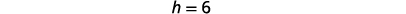    Shift grafu\(f(x)=x^{2}\) kwenye\(6\) vitengo sahihi. .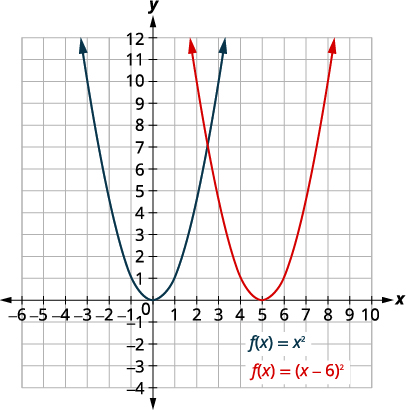
    Jedwali 9.7.2
    Zoezi\(\PageIndex{7}\)

    Grafu\(f(x)=(x−4)^{2}\) kwa kutumia mabadiliko ya usawa.

    Jibu
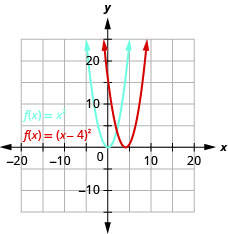
    Takwimu hii inaonyesha 2 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve kushoto ni grafu ya f ya x sawa x squared ambayo ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve haki imekuwa wakiongozwa haki 4 vitengo.
    Kielelezo 9.7.21
    Zoezi\(\PageIndex{8}\)

    Grafu\(f(x)=(x+6)^{2}\) kwa kutumia mabadiliko ya usawa.

    Jibu
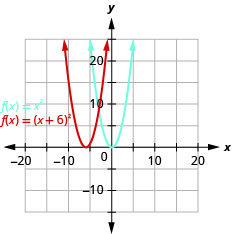
    Takwimu hii inaonyesha 2 parabolas ya kufungua juu ya ndege ya kuratibu x y. Curve haki ni grafu ya f ya x sawa x squared ambayo ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve ya kushoto imehamishwa kwenye vitengo 6 vya kushoto.
    Kielelezo 9.7.22

    Sasa kwa kuwa tunajua athari za constants\(h\) na\(k\), sisi graph kazi quadratic ya fomu\(f(x)=(x-h)^{2}+k\) kwa kuchora kwanza parabola msingi na kisha kufanya mabadiliko ya usawa ikifuatiwa na mabadiliko wima. Tunaweza kufanya mabadiliko ya wima ikifuatiwa na mabadiliko ya usawa, lakini wanafunzi wengi wanapendelea mabadiliko ya usawa ikifuatiwa na wima.

    Mfano\(\PageIndex{5}\)

    Grafu\(f(x)=(x+1)^{2}-2\) kutumia mabadiliko.

    Suluhisho:

    Kazi hii itahusisha mabadiliko mawili na tunahitaji mpango.

    Hebu tuanze kwanza kutambua mara kwa mara\(h, k\).

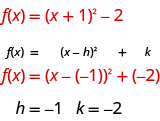
    F ya x sawa na wingi x plush 1 mraba minus 2 hutolewa kwenye mstari wa juu na f ya x sawa na quanitity x minus h h squared minis k kwenye mstari wa pili. equation aliyopewa ilibadilishwa kuwa f ya x sawa na wingi wa x bala hasi 1 squared plush hasi 2 kwenye mstari wa tatu. Mstari wa mwisho unasema h sawa na hasi 1 na k sawa na hasi 2.
    Kielelezo 9.7.23

    Mara kwa\(h\) mara inatupa mabadiliko ya usawa na\(k\) inatupa mabadiliko ya wima.

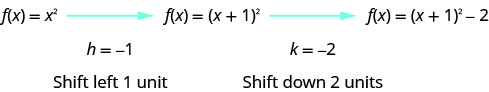
    F ya x sawa x squared hutolewa kwa mshale kutoka humo akielezea f ya x sawa na wingi x plus 1 squared na mshale kuja kutoka humo akizungumzia f ya x sawa na wingi x plus 1 squared bala 2. mistari ya kusema h sawa hasi 1 ambayo ina maana kuhama kushoto 1 kitengo na k sawa hasi 2 ambayo ina maana kuhama chini 2 vitengo.
    Kielelezo 9.7.24

    Sisi kwanza kuteka grafu ya grafu ya\(f(x)=x^{2}\) gridi ya taifa.

    Takwimu inasema kwenye mstari wa kwanza kwamba grafu ya f ya x inalingana na kiasi x plus 1 squared ni sawa na grafu ya f ya x sawa na x squared lakini kubadilishwa kushoto kitengo 1. Mstari wa pili unasema kwamba grafu ya f ya x ni sawa na kiasi x pamoja na 1 squared minus 2 ni sawa na grafu ya f ya x sawa na kiasi x plus 1 squared lakini kubadilishwa chini vitengo 2.
    Kielelezo 9.7.25
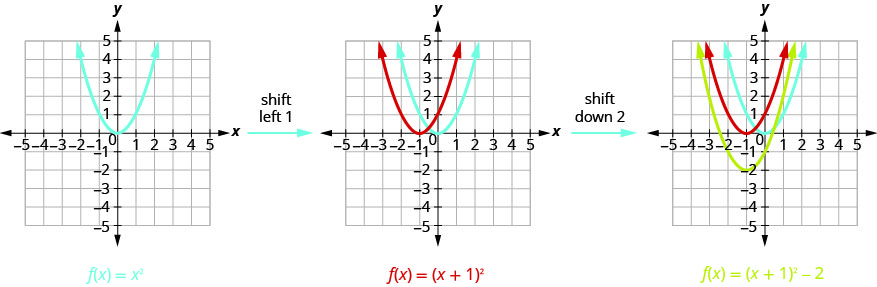
    Grafu ya kwanza inaonyesha parabola 1 ya kufungua juu kwenye ndege ya kuratibu x y. Ni grafu ya f ya x sawa x squared ambayo ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Kwa kuhama kwamba grafu ya f ya x sawa x squared kushoto 1, sisi hoja ya grafu ya pili, ambayo inaonyesha f awali ya x sawa x squared na kisha mwingine Curve wakiongozwa kushoto kitengo moja ya kuzalisha f ya x sawa na wingi wa x plus 1 squared. Kwa kusonga f ya x sawa na wingi wa x plus 1 squared chini 1, sisi kuhamia grafu ya mwisho, ambayo inaonyesha f awali ya x sawa x squared na f ya x sawa na wingi wa x plus 1, kisha mwingine Curve wakiongozwa chini 1 kuzalisha f ya x sawa na wingi wa x pamoja 1 squared minus 2.
    Kielelezo 9.7.26
    Zoezi\(\PageIndex{9}\)

    Grafu\(f(x)=(x+2)^{2}-3\) kutumia mabadiliko.

    Jibu
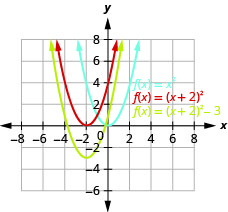
    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Moja ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Kisha, kazi ya awali ni wakiongozwa 2 vitengo kwa upande wa kushoto kuzalisha f ya x sawa na wingi wa x plus 2 squared. Curve ya mwisho huzalishwa kwa kusonga chini vitengo 3 ili kuzalisha f ya x sawa na kiasi cha x pamoja na 2 squared minus 3.
    Kielelezo 9.7.27
    Zoezi\(\PageIndex{10}\)

    Grafu\(f(x)=(x-3)^{2}+1\) kutumia mabadiliko.

    Jibu
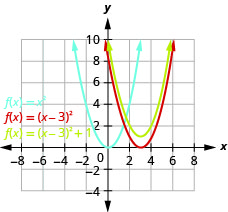
    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Moja ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Kisha, kazi ya awali ni wakiongozwa vitengo 3 na haki ya kuzalisha f ya x sawa na wingi wa x minus 3 squared. Curve ya mwisho inazalishwa kwa kusonga hadi kitengo cha 1 ili kuzalisha f ya x sawa na kiasi cha x bala 3squared pamoja na 1.
    Kielelezo 9.7.28

    Grafu Quadratic Kazi ya Fomu\(f(x)=ax^{2}\)

    Hadi sasa sisi graphed kazi quadratic\(f(x)=x^{2}\) na kisha kuona athari ya ikiwa ni pamoja na mara kwa mara\(h\) au\(k\) katika equation alikuwa juu ya grafu kusababisha ya kazi mpya. Sasa tutazingatia athari za mgawo\(a\) kwenye grafu inayosababisha kazi mpya\(f(x)=ax^{2}\).

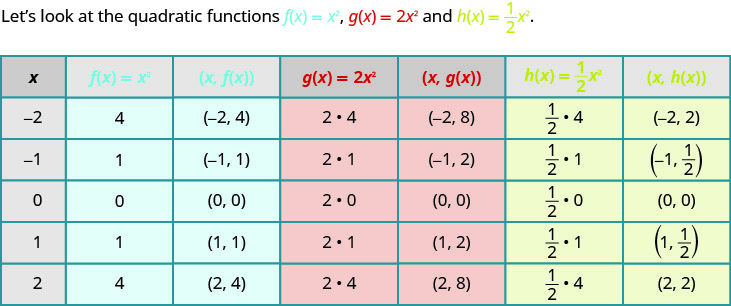
    Jedwali inayoonyesha athari za mara kwa mara kwenye kazi ya msingi ya x squared. Jedwali lina nguzo saba zilizoandikwa x, f ya x sawa x squared, jozi iliyoamriwa (x, f ya x), g ya x sawa na mara 2 x mraba, jozi iliyoamriwa (x, g ya x), h ya x sawa mara nusu x mraba, na jozi iliyoamriwa (x, h ya x). Katika safu ya x, maadili yaliyotolewa ni hasi 2, hasi 1, 0, 1, na 2. Katika f ya x sawa x safu ya mraba, maadili ni 4, 1, 0, 1, na 4. Katika safu (x, f ya x), jozi zilizoamriwa (hasi 2, 4), (hasi 1, 1), (0, 0), (1, 1), na (2, 4) zinatolewa. g ya x ni sawa na mara 2 x safu ya mraba ina maneno 2 mara 4, mara 2 1, mara 2 0, mara 2 1, na mara 2 4. Safu ya (x, g ya x) ina jozi zilizoamriwa za (hasi 2, 8), (hasi 1, 2), (0, 0), (1, 2), na (2,8). Katika h ya x sawa na nusu mara x squared, maneno yaliyotolewa ni nusu mara 4, nusu mara 1, nusu mara 0, nusu moja mara 1, na nusu mara 4. Katika safu ya mwisho, (x, h ya x), ina jozi zilizoagizwa (hasi 2, 2), (hasi 1, nusu moja), (0, 0), (1, nusu moja), na (2, 2).
    Kielelezo 9.7.29

    Kama sisi grafu kazi hizi, tunaweza kuona athari za mara kwa mara\(a\), kuchukua\(a>0\).

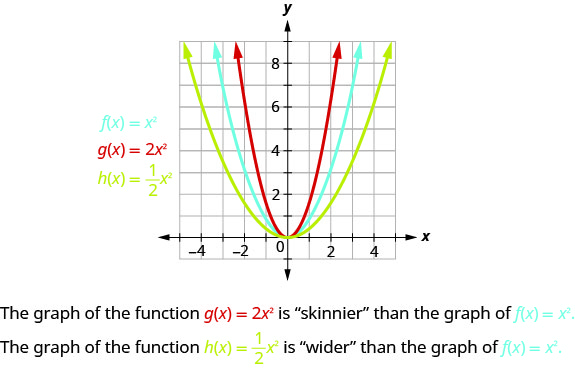
    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Moja ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve slimmer ya g ya x sawa 2 mara x mraba ina kipeo katika (0,0) na pointi nyingine za (hasi 1, nusu moja) na (1, nusu moja). Curve pana, h ya x sawa na nusu x mraba, ina kipeo katika (0,0) na pointi nyingine za (hasi 2, 2) na (2,2).
    Kielelezo 9.7.30

    Ili kuchora kazi na mara kwa mara\(a\) ni rahisi kuchagua pointi chache\(f(x)=x^{2}\) na kuzidisha\(y\) -maadili na\(a\).

    Grafu ya Kazi ya Quadratic ya Fomu\(f(x)=ax^{2}\)

    Mgawo\(a\) katika kazi\(f(x)=ax^{2}\) huathiri grafu ya\(f(x)=x^{2}\) kwa kunyoosha au kuimarisha.

    • Ikiwa\(0<|a|<1\), grafu ya\(f(x)=ax^{2}\) itakuwa “pana” kuliko grafu ya\(f(x)=x^{2}\).
    • Kama\(|a|>1\), grafu ya\(f(x)=ax^{2}\) itakuwa “skinnier” kuliko grafu ya\(f(x)=x^{2}\).
    Mfano\(\PageIndex{6}\)

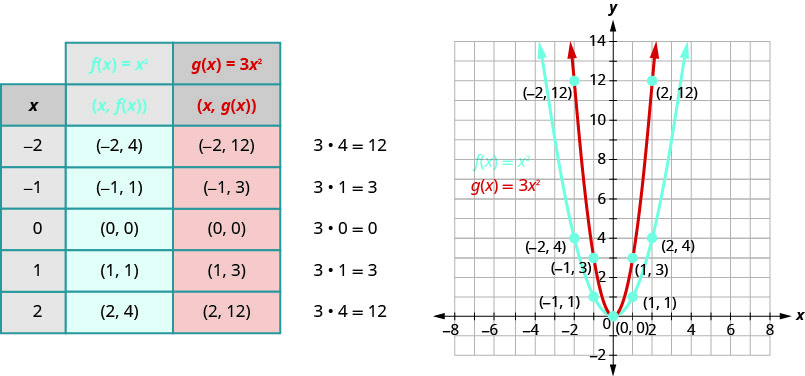
    Grafu\(f(x)=3x^{2}\).

    Suluhisho:

    Tutaweka graph kazi\(f(x)=x^{2}\) na\(g(x)=3x^{2}\) kwenye gridi hiyo. Sisi kuchagua pointi chache juu\(f(x)=x^{2}\) na kisha kuzidisha\(y\) -maadili na\(3\) kupata pointi kwa\(g(x)=3x^{2}\).

    Jedwali linaonyesha athari za mara kwa mara kwenye kazi ya msingi ya x squared. Jedwali lina nguzo 3 zilizoandikwa x, f ya x sawa x mraba na jozi iliyoamriwa (x, f ya x), na g ya x sawa na mara 3 x mraba na jozi iliyoamriwa (x, g ya x). Katika safu ya x, maadili yaliyotolewa ni hasi 2, hasi 1, 0, 1, na 2. Katika f ya x sawa x mraba na jozi iliyoamriwa (x, f ya x), jozi zilizoamriwa (hasi 2, 4), (hasi 1, 1), (0, 0), (1, 1), na (2, 4) zinatolewa. g ya x sawa 3 mara x squared na jozi kuamuru (x, g ya x) safu ina jozi awali ya (hasi 2, 12) kwa sababu 3 mara 4 ni sawa na 12, (hasi 1, 3) kwa sababu 3 mara 1 ni sawa na 3, (0, 0) kwa sababu 3 mara 0 sawa na 0, (1, 3) kwa sababu 3 mara 1 sawa na 3, na (2,12) kwa sababu mara 3 4 sawa na 12. Grafu kando ya meza inaonyesha 2 parabolas ya kufungua juu kwenye ndege ya kuratibu x y. Moja ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Vipengele vingine vilivyotolewa kwenye safu viko kwenye (hasi 2, 4) (hasi 1, 1), (1, 1), na (2,4). Curve ndogo ya g ya x sawa na mara 3 x squared ina kipeo katika (0,0) na pointi nyingine iliyotolewa ya (hasi 2, 12), (hasi 1, 3), (1, 3), na (2,12).
    Kielelezo 9.7.31
    Zoezi\(\PageIndex{11}\)

    Grafu\(f(x)=-3x^{2}\).

    Jibu
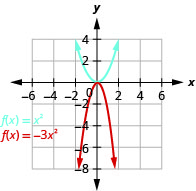
    Grafu inaonyesha parabola ya juu-kufungua kwenye ndege ya kuratibu x y ya f ya x sawa x squared ambayo ina kipeo cha (0, 0). Vipengele vingine vilivyotolewa kwenye safu viko kwenye (hasi 2, 4) (hasi 1, 1), (1, 1), na (2,4). Pia inavyoonekana ni parabola chini-kufungua ya f ya x sawa hasi 3 mara x squared. Ina kipeo cha (0,0) na pointi nyingine katika (hasi 1, hasi 3) na (1, hasi 3)
    Kielelezo 9.7.32
    Zoezi\(\PageIndex{12}\)

    Grafu\(f(x)=2x^{2}\).

    Jibu
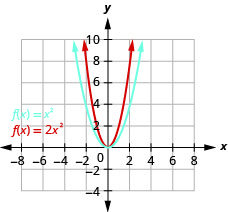
    Takwimu hii inaonyesha 2 parabolas ya kufungua juu ya ndege ya kuratibu x y. Moja ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve slimmer ya f ya x sawa 2 mara x mraba ina kipeo katika (0,0) na pointi nyingine za (hasi 1, nusu moja) na (1, nusu moja).
    Kielelezo 9.7.33

    Grafu Quadratic Kazi Kutumia Mabadiliko

    Tumejifunza jinsi constants\(a, h\), na\(k\) katika kazi,\(f(x)=x^{2}+k, f(x)=(x−h)^{2}\), na\(f(x)=ax^{2}\) kuathiri grafu zao. Sasa tunaweza kuweka hii pamoja na grafu kazi quadratic\(f(x)=ax^{2}+bx+c\) kwa kwanza kuziweka katika fomu\(f(x)=a(x−h)^{2}+k\) kwa kukamilisha mraba. Fomu hii wakati mwingine hujulikana kama fomu ya kipeo au fomu ya kawaida.

    Lazima tuwe makini kwa wote kuongeza na kuondoa idadi kwa upande SAME wa kazi ili kukamilisha mraba. Hatuwezi kuongeza namba kwa pande zote mbili kama tulivyofanya tulipomaliza mraba na equations quadratic.

    Takwimu hii inaonyesha tofauti wakati wa kukamilisha mraba na equation quadratic na kazi ya quadratic. Kwa equation quadratic, kuanza na x squared pamoja 8 mara x pamoja 6 sawa na sifuri. Ondoa 6 kutoka pande zote mbili ili kupata x mraba pamoja na mara 8 x sawa na hasi 6 huku ukiacha nafasi ili kukamilisha mraba. Kisha, kukamilisha mraba kwa kuongeza 16 kwa pande zote mbili kupata x squared plush mara 8 x plush 16 sawa hasi 6 plush 16. Sababu ya kupata kiasi x pamoja na 4 squared sawa 10. Kwa kazi quadratic, kuanza na f ya x sawa x squared pamoja 8 mara x plus 6. Mstari wa pili unaonyesha kuondoka nafasi kati ya mara 8 x na 6 ili kukamilisha mraba. Kukamilisha mraba kwa kuongeza 16 na kutoa 16 upande huo kupata f ya x sawa x squared pamoja na mara 8 x plush 16 pamoja na 6 minus 16. Sababu ya kupata f ya x sawa na wingi wa x plush 4 squared minus 10.
    Kielelezo 9.7.34

    Tunapokamilisha mraba katika kazi na mgawo wa\(x^{2}\) hiyo sio moja, tunapaswa kuzingatia mgawo huo kutoka kwa\(x\) maneno tu. Hatuna sababu hiyo kutoka kwa muda wa mara kwa mara. Mara nyingi husaidia kusonga muda wa mara kwa mara kidogo kwa haki ili iwe rahisi kuzingatia tu\(x\) -masharti.

    Mara tu tunapopata mara kwa mara tunataka kukamilisha mraba, lazima tukumbuke kuzidisha kwa mgawo huo kabla ya kuiondoa.

    Mfano\(\PageIndex{7}\)

    Andika upya\(f(x)=−3x^{2}−6x−1\) kwa\(f(x)=a(x−h)^{2}+k\) fomu kwa kukamilisha mraba.

    Suluhisho:

      .
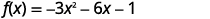    Toa\(x\) maneno kutoka kwa mara kwa mara. .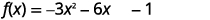
    Sababu ya mgawo wa\(x^{2}, -3\). .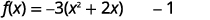
    Jitayarishe kukamilisha mraba. .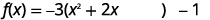
    Kuchukua nusu ya\(2\) na kisha mraba ni kukamilisha mraba\((\frac{1}{2}\cdot 2)^{2}=1\)  
    Mara kwa mara\(1\) hukamilisha mraba katika mabano, lakini mabano huongezeka kwa\(-3\). Hivyo sisi ni kweli kuongeza\(-3\). Ni lazima kisha\(3\) kuongeza na mabadiliko ya thamani ya kazi. .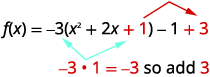
    Andika upya trinomial kama mraba na uondoe vipindi. .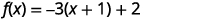
    Kazi sasa iko katika\(f(x)=a(x-h)^{2}+k\) fomu. .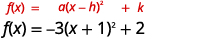
    Jedwali 9.7.3
    Zoezi\(\PageIndex{13}\)

    Andika upya\(f(x)=−4x^{2}−8x+1\) kwa\(f(x)=a(x−h)^{2}+k\) fomu kwa kukamilisha mraba.

    Jibu

    \(f(x)=-4(x+1)^{2}+5\)

    Zoezi\(\PageIndex{14}\)

    Andika upya\(f(x)=2x^{2}−8x+3\) kwa\(f(x)=a(x−h)^{2}+k\) fomu kwa kukamilisha mraba.

    Jibu

    \(f(x)=2(x-2)^{2}-5\)

    Mara baada ya kuweka kazi katika\(f(x)=(x−h)^{2}+k\) fomu, tunaweza kisha kutumia mabadiliko kama tulivyofanya katika matatizo machache iliyopita. Mfano unaofuata utatuonyesha jinsi ya kufanya hivyo.

    Mfano\(\PageIndex{8}\)

    Grafu\(f(x)=x^{2}+6x+5\) kwa kutumia mabadiliko.

    Suluhisho:

    Hatua ya 1: Andika upya kazi katika fomu ya\(f(x)=a(x-h)^{2}+k\) vertex kwa kukamilisha mraba.

      .
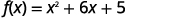    Toa\(x\) maneno kutoka kwa mara kwa mara. .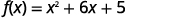
    Chukua nusu ya\(6\) na kisha mraba ili kukamilisha mraba. \((\frac{1}{2}\cdot 6)^{2}=9\)  
    Sisi wote kuongeza\(9\) na Ondoa\(9\) ili kubadilisha thamani ya kazi. .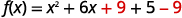
    Andika upya trinomial kama mraba na uondoe vipindi. .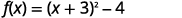
    Kazi sasa iko katika\(f(x)=(x-h)^{2}+k\) fomu. .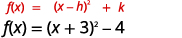
    Jedwali 9.7.4

    Hatua ya 2: Graph kazi kwa kutumia mabadiliko.

    Kuangalia\(h, k\) maadili, tunaona grafu itachukua grafu ya\(f(x)=x^{2}\) na kuibadilisha kwenye vitengo vya kushoto na\(3\) vitengo\(4\) vya chini.

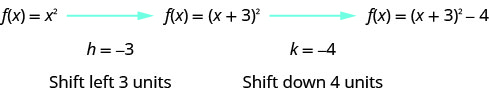
    F ya x sawa x squared hutolewa kwa mshale kutoka humo akielezea f ya x sawa na wingi x plus 3 squared na mshale kuja kutoka humo akizungumzia f ya x sawa na wingi x plus 3 squared minus 4. Mstari unaofuata unasema h sawa na hasi 3 ambayo inamaanisha kuhama kushoto kitengo cha 3 na k sawa na hasi 4 ambayo inamaanisha kuhama chini vitengo 4
    Kielelezo 9.7.47

    Sisi kwanza kuteka grafu ya grafu ya\(f(x)=x^{2}\) gridi ya taifa.

    Kwa grafu f ya x sawa na kiasi x plus 3 squared, kuhama grafu ya f ya x sawa x mraba kwa vitengo 3 kushoto. Kwa grafu f ya x sawa na kiasi x pamoja na 3 squared minus 4, kuhama grafu kiasi x pamoja 3 squared chini vitengo 4.
    Kielelezo 9.7.48
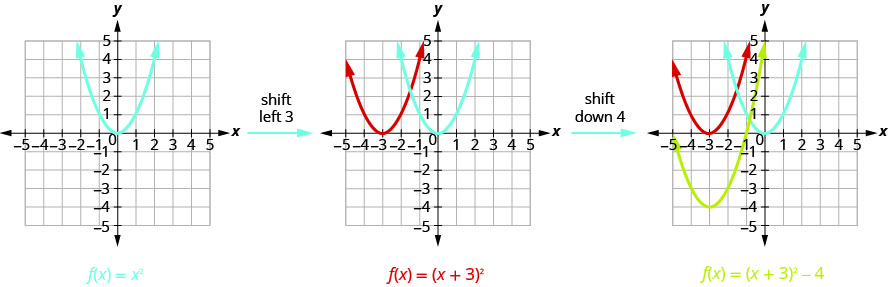
    Grafu ya kwanza inaonyesha parabola 1 ya kufungua juu kwenye ndege ya kuratibu x y. Ni grafu ya f ya x sawa x squared ambayo ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Kwa kuhama kwamba grafu ya f ya x sawa x squared kushoto 3, sisi hoja ya grafu ya pili, ambayo inaonyesha f awali ya x sawa x squared na kisha mwingine Curve wakiongozwa kushoto vitengo 3 kuzalisha f ya x sawa na wingi wa x plus 3 squared. Kwa kusonga f ya x sawa na wingi wa x plus 3 squared chini 2, sisi kuhamia grafu ya mwisho, ambayo inaonyesha f awali ya x sawa x squared na f ya x sawa na wingi wa x plus 3 squared, kisha mwingine Curve wakiongozwa chini 4 kuzalisha f ya x sawa na wingi wa x pamoja 1 squared minus 4.
    Kielelezo 9.7.49
    Zoezi\(\PageIndex{15}\)

    Grafu\(f(x)=x^{2}+2x-3\) kwa kutumia mabadiliko.

    Jibu
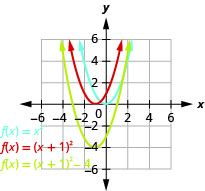
    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Moja ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve upande wa kushoto imehamishwa kitengo 1 upande wa kushoto ili kuzalisha f ya x sawa na wingi wa x plus 1 squared. Grafu ya tatu imehamishwa chini ya vitengo 4 ili kuzalisha f ya x sawa na kiasi cha x pamoja na 1 mraba minus 4.
    Kielelezo 9.7.50
    Zoezi\(\PageIndex{16}\)

    Grafu\(f(x)=x^{2}-8x+12\) kwa kutumia mabadiliko.

    Jibu
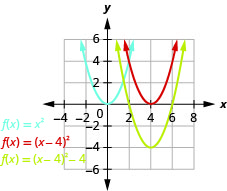
    Takwimu hii inaonyesha 3 parabolas ya kufungua juu ya ndege ya kuratibu x y. Moja ni grafu ya f ya x sawa x squared na ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Curve kwa haki imehamishwa vitengo 4 kwa haki ya kuzalisha f ya x sawa na wingi wa x minus 4 squared. Grafu ya tatu imehamishwa chini ya vitengo 4 ili kuzalisha f ya x sawa na kiasi cha x minus 4 squared minus 4.
    Kielelezo 9.7.51

    Tunaandika hatua za kuchukua grafu kazi ya quadratic kwa kutumia mabadiliko hapa.

    Grafu Kazi ya Quadratic Kutumia Mabadiliko

    1. Andika upya kazi kwa\(f(x)=a(x-h)^{2}+k\) fomu kwa kukamilisha mraba.
    2. Graph kazi kwa kutumia mabadiliko.
    Mfano\(\PageIndex{9}\)

    Grafu\(f(x)=-2x^{2}-4x+2\) kwa kutumia mabadiliko.

    Suluhisho:

    Hatua ya 1: Andika upya kazi katika fomu ya\(f(x)=a(x-h)^{2}+k\) vertex kwa kukamilisha mraba.

      .
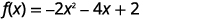    Toa\(x\) maneno kutoka kwa mara kwa mara. .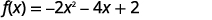
    Tunahitaji mgawo\(x^{2}\) wa kuwa moja. Sisi sababu\(-2\) kutoka\(x\) -masharti. .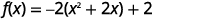
    Chukua nusu ya\(2\) na kisha mraba ili kukamilisha mraba. \((\frac{1}{2}\cdot 2)^{2}=1\)  
    Tunaongeza\(1\) kukamilisha mraba katika mabano, lakini mabano huongezeka kwa\(-2\). Hivyo sisi ni kweli kuongeza\(-2\). Ili kubadilisha thamani ya kazi tunayoongeza\(2\). .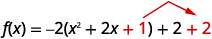
    Andika upya trinomial kama mraba na uondoe vipindi. .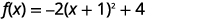
    Kazi sasa iko katika\(f(x)=a(x-h)^{2}+k\) fomu. .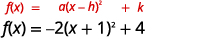
    Jedwali 9.7.5

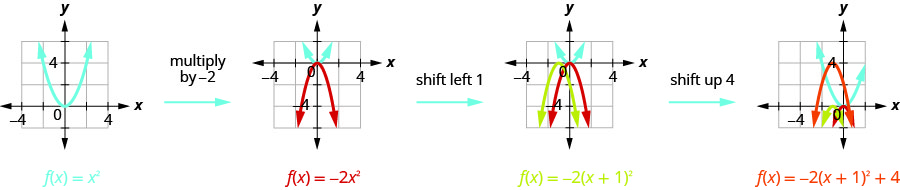
    Hatua ya 2: Graph kazi kwa kutumia mabadiliko.

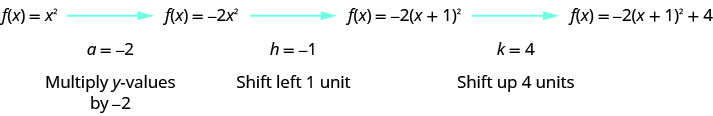
    F ya x sawa x squared hutolewa kwa mshale kutoka humo akielezea f ya x sawa na hasi 2 mara x squared na mshale kuja kutoka humo akizungumzia f ya x sawa hasi mara 2 kiasi x plus 1 squared. mshale kuja kutoka humo kwa uhakika wa f ya x sawa hasi 2 mara wingi x plus 1 squared pamoja 4. Mstari unaofuata unasema sawa na hasi 2 ambayo ina maana kuzidisha maadili ya y na hasi 2, kisha h sawa na hasi 1 ambayo ina maana kuhama kushoto 1 kitengo na k sawa 4 ambayo ina maana kuhama hadi 4 vitengo
    Kielelezo 9.7.58

    Sisi kwanza kuteka grafu ya grafu ya\(f(x)=x^{2}\) gridi ya taifa.

    Kwa grafu f ya x sawa na hasi 2 mara x squared, kuzidisha y maadili katika parabola ya f ya x sawa x squared na hasi 2. Kwa grafu f ya x sawa na hasi mara 2 kiasi x plus 1 squared, kuhama grafu ya f ya x sawa hasi mara 2 x mraba kwa kitengo cha kushoto 1. Kwa grafu f ya x sawa na hasi mara 2 kiasi x plus 1 squared pamoja 4, kuhama grafu ya f ya x sawa hasi mara 2 kiasi x pamoja 1 squared up 4 vitengo.
    Kielelezo 9.7.59
    Grafu ya kwanza inaonyesha parabola 1 ya kufungua juu kwenye ndege ya kuratibu x y. Ni grafu ya f ya x sawa x squared ambayo ina kipeo cha (0, 0). Pointi nyingine juu ya Curve ziko katika (hasi 1, 1) na (1, 1). Kwa kuzidisha kwa hasi 2, nenda kwenye grafu inayofuata inayoonyesha f ya awali ya x sawa x mraba na slimmer mpya na flipped grafu ya f ya x sawa hasi 2 x squared. Kwa kuhama kwamba grafu ya f ya x sawa na hasi 2 mara x squared kushoto 1, sisi kuhamia grafu ya pili, ambayo inaonyesha f awali ya x sawa x squared, f ya x sawa hasi 2 x squared, na kisha mwingine Curve wakiongozwa kushoto 1 kitengo kuzalisha f ya x sawa hasi mara 2 wingi wa x pamoja 1 squared. Kwa kusonga f ya x sawa na hasi mara 2 wingi wa x pamoja 1 squared up 4, sisi kuhamia grafu ya mwisho, ambayo inaonyesha f awali ya x sawa x squared, f ya x sawa hasi 2 x squared, na f ya x sawa hasi 2 mara wingi wa x plus 1 squared, kisha mwingine Curve wakiongozwa hadi 4 kuzalisha f ya x sawa na hasi 2 mara wingi wa x pamoja 1 squared plus 4.
    Kielelezo 9.7.60
    Zoezi\(\PageIndex{17}\)

    Grafu\(f(x)=-3x^{2}+12x-4\) kwa kutumia mabadiliko.

    Jibu
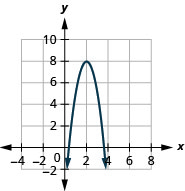
    Takwimu hii inaonyesha parabola ya kufungua chini kwenye ndege ya kuratibu x y na kipeo cha (2,8) na pointi nyingine za (1,5) na (3,5).
    Kielelezo 9.7.61
    Zoezi\(\PageIndex{18}\)

    Grafu\(f(x)=−2x^{2}+12x−9\) kwa kutumia mabadiliko.

    Jibu
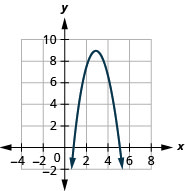
    Takwimu hii inaonyesha parabola ya kufungua chini kwenye ndege ya kuratibu x y na kipeo cha (3, 9) na pointi nyingine za (1, 1) na (5, 1).
    Kielelezo 9.7.62

    Sasa kwa kuwa tumekamilisha mraba ili kuweka kazi ya quadratic katika\(f(x)=a(x−h)^{2}+k\) fomu, tunaweza pia kutumia mbinu hii kwa graph kazi kwa kutumia mali zake kama katika sehemu ya awali.

    Kama sisi kuangalia nyuma katika mifano michache iliyopita, tunaona kwamba kipeo ni kuhusiana na constants\(h\) na\(k\).

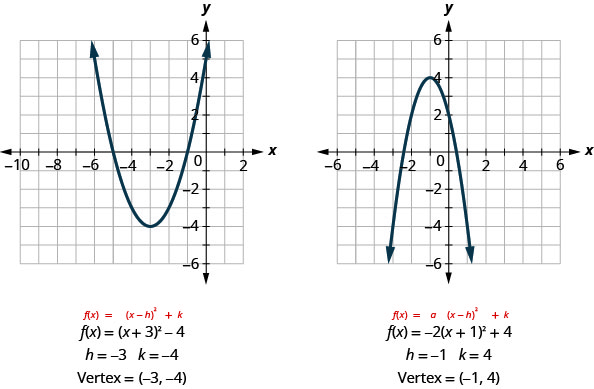
    Grafu ya kwanza inaonyesha parabola ya juu-kufungua kwenye ndege ya kuratibu x y na kipeo cha (hasi 3, hasi 4) na pointi nyingine za (0, hasi 5) na (0, hasi 1). Chini ya grafu, inaonyesha fomu ya kawaida ya parabola, f ya x sawa na kiasi x bala h squared pamoja k, na equation ya parabola f ya x sawa na wingi wa x pamoja 3 squared minus 4 ambapo h sawa hasi 3 na k sawa na hasi 4. Grafu ya pili inaonyesha parabola ya kufungua chini kwenye ndege ya kuratibu x y na kipeo cha (hasi 1, 4) na pointi nyingine za (0,2) na (hasi 2,2). Chini ya grafu, inaonyesha fomu ya kawaida ya parabola, f ya x sawa mara kiasi x bala h squared pamoja k, na equation ya parabola f ya x sawa hasi mara 2 wingi wa x pamoja 1 squared pamoja 4 ambapo h sawa na hasi 1 na k sawa na 4.
    Kielelezo 9.7.63

    Katika kila kesi, vertex ni\((h,k)\). Pia mhimili wa ulinganifu ni mstari\(x=h\).

    Tunaandika tena hatua zetu za kuchora kazi ya quadratic kwa kutumia mali kwa wakati kazi iko katika\(f(x)=a(x−h)^{2}+k\) fomu.

    Grafu Kazi ya Quadratic katika Fomu\(f(x)=a(x-h)^{2}+k\) Kutumia Mali

    1. Andika upya\(f(x)=a(x-h)^{2}+k\) fomu ya kazi.
    2. Kuamua kama parabola kufungua juu,\(a>0\), au chini,\(a<0\).
    3. Pata mhimili wa ulinganifu,\(x=h\).
    4. Pata vertex,\((h,k\).
    5. Pata\(y\) -intercept. Pata uhakika ulinganifu kwa\(y\) -intercept katika mhimili wa ulinganifu.
    6. Kupata\(x\) -intercepts.
    7. Grafu parabola.
    Mfano\(\PageIndex{10}\)
    1. Andika upya\(f(x)=2 x^{2}+4 x+5\) kwa\(f(x)=a(x-h)^{2}+k\) fomu
    2. Graph kazi kwa kutumia mali

    Suluhisho:

    Andika upya kazi kwa\(f(x)=a(x-h)^{2}+k\) fomu kwa kukamilisha mraba. \(f(x)=2 x^{2}+4 x+5\)
      \(f(x)=2\left(x^{2}+2 x\right)+5\)
      \(f(x)=2\left(x^{2}+2 x+1\right)+5-2\)
      \(f(x)=2(x+1)^{2}+3\)
    Tambua mara kwa mara\(a, h, k\). \(a=2 h=-1 k=3\)
    Tangu\(a=2\), parabola inafungua juu. .
    Mhimili wa ulinganifu ni\(x=h\). Mhimili wa ulinganifu ni\(x=-1\).
    Vertex ni\((h,k)\). Vertex ni\((-1,3)\).
    Kupata\(y\) -intercept kwa kutafuta\(f(0)\). \(f(0)=2 \cdot 0^{2}+4 \cdot 0+5\)
      \(f(0)=5\)
      \(y\)-kukatiza\((0,5)\)
    Pata hatua ya\((0,5)\) ulinganifu kwenye mhimili wa ulinganifu. \((-2,5)\)
    Kupata\(x\) -intercepts. Wabaguzi ni hasi, kwa hiyo hakuna\(x\) -intercepts. Grafu parabola.
      .
    Jedwali 9.7.6
    Zoezi\(\PageIndex{19}\)
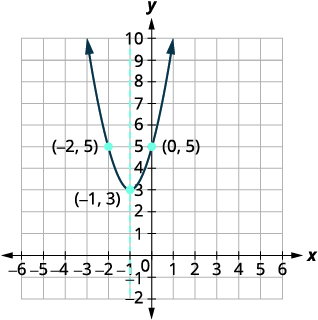    1. Andika upya\(f(x)=3 x^{2}-6 x+5\) kwa\(f(x)=a(x-h)^{2}+k\) fomu
    2. Graph kazi kwa kutumia mali
    Jibu
    1. \(f(x)=3(x-1)^{2}+2\)

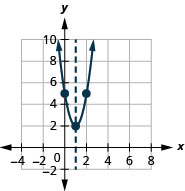
    2. Grafu iliyoonyeshwa ni parabola inayoelekea juu na vertex (1, 2) na y-intercept (0, 5). Mhimili wa ulinganifu umeonyeshwa, x sawa na 1.
      Kielelezo 9.7.66
    Zoezi\(\PageIndex{20}\)
    1. Andika upya\(f(x)=-2 x^{2}+8 x-7\) kwa\(f(x)=a(x-h)^{2}+k\) fomu
    2. Graph kazi kwa kutumia mali
    Jibu
    1. \(f(x)=-2(x-2)^{2}+1\)

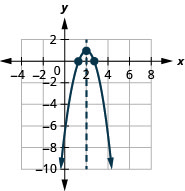
    2. Grafu iliyoonyeshwa ni chini inakabiliwa na parabola na vertex (2, 1) na x-intercepts (1, 0) na (3, 0). Mhimili wa ulinganifu umeonyeshwa, x sawa na 2.
      Kielelezo 9.7.67

    Pata Kazi ya Quadratic kutoka kwenye Grafu yake

    Hadi sasa tumeanza na kazi na kisha kupatikana grafu yake.

    Sasa tutaenda kurekebisha mchakato. Kuanzia na grafu, tutapata kazi.

    Mfano\(\PageIndex{11}\)

    Tambua kazi ya quadratic ambayo grafu inavyoonyeshwa.

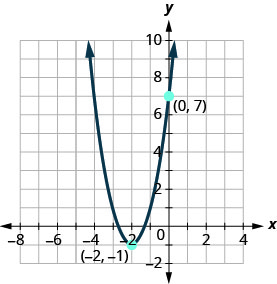
    Grafu iliyoonyeshwa ni juu inakabiliwa na parabola na vertex (hasi 2, hasi 1) na y-intercept (0, 7).
    Kielelezo 9.7.68

    Suluhisho:

    Kwa kuwa ni quadratic, tunaanza na\(f(x)=a(x−h)^{2}+k\) fomu.

    Vertex,\((h,k)\), ni\((−2,−1)\) hivyo\(h=−2\) na\(k=−1\).

    \(f(x)=a(x-(-2))^{2}-1\)

    Ili kupata\(a\), tunatumia\(y\) -intercept,\((0,7)\).

    Hivyo\(f(0)=7\).

    \(7=a(0+2)^{2}-1\)

    Kutatua kwa\(a\).

    \(\begin{array}{l}{7=4 a-1} \\ {8=4 a} \\ {2=a}\end{array}\)

    Andika kazi.

    \(f(x)=a(x-h)^{2}+k\)

    Mbadala katika\(h=-2, k=-1\) na\(a=2\).

    \(f(x)=2(x+2)^{2}-1\)

    Zoezi\(\PageIndex{21}\)

    Andika kazi ya quadratic kwa\(f(x)=a(x−h)^{2}+k\) fomu ambayo grafu inavyoonyeshwa.

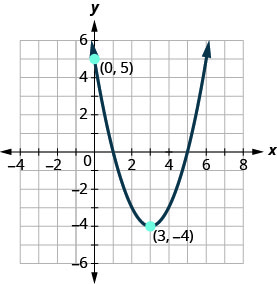
    Grafu iliyoonyeshwa ni parabola inayoelekea juu na vertex (3, hasi 4) na y-intercept (0, 5).
    Kielelezo 9.7.69
    Jibu

    \(f(x)=(x-3)^{2}-4\)

    Zoezi\(\PageIndex{22}\)

    Tambua kazi ya quadratic ambayo grafu inavyoonyeshwa.

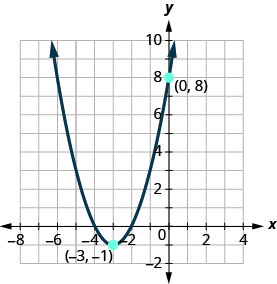
    Grafu iliyoonyeshwa ni parabola inayoelekea juu na vertex (hasi 3, hasi 1) na y-intercept (0, 8).
    Kielelezo 9.7.70
    Jibu

    \(f(x)=(x+3)^{2}-1\)

    Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kazi za quadratic za kuchora kwa kutumia mabadiliko.

    Dhana muhimu

    • Grafu Kazi ya Quadratic ya fomu\(f(x)=x^{2}+k\) Kutumia Shift ya Wima
      • Grafu ya\(f(x)=x^{2}+k\) mabadiliko grafu ya\(k\) vitengo vya\(f(x)=x^{2}\) wima.
        • Kama\(k>0\), kuhama parabola wima up\(k\) vitengo.
        • Kama\(k<0\), kuhama parabola wima chini\(|k|\) vitengo.
    • Grafu Kazi ya Quadratic ya fomu\(f(x)=(x−h)^{2}\) Kutumia Shift Horizontal
      • Grafu ya\(f(x)=(x−h)^{2}\) mabadiliko grafu ya\(h\) vitengo vya\(f(x)=x^{2}\) usawa.
        • Kama\(h>0\), kuhama parabola usawa\(h\) vitengo kushoto.
        • Kama\(h<0\), kuhama parabola usawa\(|h|\) vitengo haki.
    • Grafu ya Kazi ya Quadratic ya fomu\(f(x)=ax^{2}\)
      • Mgawo\(a\) katika kazi\(f(x)=ax^{2}\) huathiri grafu ya\(f(x)=x^{2}\) kwa kunyoosha au kuimarisha.
        Ikiwa\(0<|a|<1\), basi grafu ya\(f(x)=ax^{2}\) itakuwa “pana” kuliko grafu ya\(f(x)=x^{2}\).
        Ikiwa\(|a|>1\), basi grafu ya\(f(x)=ax^{2}\) itakuwa “skinnier” kuliko grafu ya\(f(x)=x^{2}\).
    • Jinsi ya kuchora kazi ya quadratic kwa kutumia mabadiliko
      1. Andika upya kazi kwa\(f(x)=a(x−h)^{2}+k\) fomu kwa kukamilisha mraba.
      2. Graph kazi kwa kutumia mabadiliko.
    • Grafu kazi ya quadratic katika fomu ya vertex\(f(x)=a(x−h)^{2}+k\) kutumia mali
      1. Andika upya kazi kwa\(f(x)=a(x−h)^{2}+k\) fomu.
      2. Kuamua kama parabola kufungua juu,\(a>0\), au chini,\(a<0\).
      3. Pata mhimili wa ulinganifu,\(x=h\).
      4. Pata vertex,\((h,k)\).
      5. Pata\(y\) -intercept. Pata uhakika ulinganifu kwa\(y\) -intercept katika mhimili wa ulinganifu.
      6. Kupata\(x\) -intercepts, kama inawezekana.
      7. Grafu parabola.