Skip to main content
Global

8.2: Kurahisisha Maneno na Mizizi

  1. Last updated
  2. Save as PDF
  • Page ID
    176266

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Punguza maneno na mizizi
    • Tathmini na mizizi ya takriban
    • Punguza maneno ya kutofautiana na mizizi

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kurahisisha: a.\((−9)^{2}\) b.\(-9^{2}\) c.\((−9)^{3}\)
      kama amekosa tatizo hili, mapitio Mfano 2.21.
    2. \(3.846\)Pande zote hadi karibu na mia moja.
      Kama amekosa tatizo hili, mapitio Mfano 1.34.
    3. Kurahisisha: a.\(x^{3} \cdot x^{3}\) b.\(y^{2} \cdot y^{2} \cdot y^{2}\) c.\(z^{3} \cdot z^{3} \cdot z^{3} \cdot z^{3}\)
      kama amekosa tatizo hili, mapitio Mfano 5.12.

    Rahisisha Maneno na Mizizi

    Katika Misingi, tuliangalia kwa ufupi mizizi ya mraba. Kumbuka kwamba wakati nambari halisi\(n\) inapoongezeka kwa yenyewe, tunaandika\(n^{2}\) na kuisoma '\(n^{2}\)mraba'. Nambari hii inaitwa mraba wa\(n\), na\(n\) inaitwa mizizi ya mraba. Kwa mfano,

    \(13^{2}\)inasoma "\(13\)mraba”

    \(169\)inaitwa mraba wa\(13\), tangu\(13^{2}=169\)

    \(13\)ni mizizi ya mraba ya\(169\)

    Ufafanuzi\(\PageIndex{1}\): Square and Square Root of a Number

    Square

    Ikiwa\(n^{2}=m\), basi\(m\) ni mraba wa\(n\).

    Mizizi ya mraba

    Ikiwa\(n^{2}=m\), basi\(n\) ni mizizi ya mraba ya\(m\).

    Taarifa\((−13)^{2} = 169\) pia, hivyo pia\(−13\) ni mizizi ya mraba ya\(169\). Kwa hiyo, wote wawili\(13\) na\(−13\) ni mizizi ya mraba ya\(169\).

    Kwa hiyo, kila idadi nzuri ina mizizi miwili ya mraba-moja chanya na moja hasi. Nini kama sisi tu alitaka chanya mraba mizizi ya idadi chanya? Sisi kutumia ishara radical, na kuandika\(\sqrt{m}\), ambayo inaashiria chanya mraba mizizi ya\(m\). Mzizi mzuri wa mraba pia huitwa mizizi kuu ya mraba.

    Tunatumia pia ishara kubwa kwa mizizi ya mraba ya sifuri. Kwa sababu\(0^{2}=0, \sqrt{0}=0\). Angalia kwamba sifuri ina mizizi moja tu ya mraba.

    Ufafanuzi\(\PageIndex{2}\): Square Root Notation

    \(\sqrt{m}\)ni kusoma “mizizi mraba ya\(m\).”

    Ikiwa\(n^{2}=m\), basi\(n=\sqrt{m}\), kwa\(n\geq 0\).

    \[\color{cyan} \text{radical sign} \longrightarrow \color{black} \sqrt{m} \color{cyan} \longleftarrow \text{radicand} \nonumber\]
    Kielelezo 8.1.1

    Tunajua kwamba kila nambari nzuri ina mizizi miwili ya mraba na ishara kubwa inaonyesha moja nzuri. Tunaandika\(\sqrt{169}=13\). Ikiwa tunataka kupata mizizi ya mraba hasi ya nambari, tunaweka hasi mbele ya ishara kubwa. Kwa mfano,\(-\sqrt{169}=-13\).

    Mfano\(\PageIndex{1}\)

    Kurahisisha:

    1. \(\sqrt{144}\)
    2. \(-\sqrt{289}\)

    Suluhisho:

    a.

    \(\sqrt{144}\)

    Tangu\(12^{2}=144\).

    \(12\)

    b.

    \(-\sqrt{289}\)

    Tangu\(17^{2}=289\) na hasi ni mbele ya ishara kubwa.

    \(-17\)

    Zoezi\(\PageIndex{1}\)

    Kurahisisha:

    1. \(-\sqrt{64}\)
    2. \(\sqrt{225}\)
    Jibu
    1. \(-8\)
    2. \(15\)
    Zoezi\(\PageIndex{2}\)

    Kurahisisha:

    1. \(\sqrt{100}\)
    2. \(-\sqrt{121}\)
    Jibu
    1. \(10\)
    2. \(-11\)

    Je, tunaweza kurahisisha\(-\sqrt{49}\)? Je, kuna idadi ambayo mraba ni\(-49\)?

    \((\)___\( )^{2}=-49\)

    Nambari yoyote nzuri ya mraba ni chanya. Nambari yoyote mbaya ya mraba ni chanya. Hakuna idadi halisi sawa na\(\sqrt{-49}\). Mzizi wa mraba wa namba hasi sio namba halisi.

    Mfano\(\PageIndex{2}\)

    Kurahisisha:

    1. \(\sqrt{-196}\)
    2. \(-\sqrt{64}\)

    Suluhisho:

    a.

    \(\sqrt{-196}\)

    Hakuna idadi halisi ambayo mraba ni\(-196\).

    \(\sqrt{-196}\)si idadi halisi.

    b.

    \(-\sqrt{64}\)

    Hasi ni mbele ya radical.

    \(-8\)

    Zoezi\(\PageIndex{3}\)

    Kurahisisha:

    1. \(\sqrt{-169}\)
    2. \(-\sqrt{81}\)
    Jibu
    1. si idadi halisi
    2. \(-9\)
    Zoezi\(\PageIndex{4}\)

    Kurahisisha:

    1. \(-\sqrt{49}\)
    2. \(\sqrt{-121}\)
    Jibu
    1. \(-7\)
    2. si idadi halisi

    Hadi sasa tumezungumzia tu kuhusu mraba na mizizi ya mraba. Hebu sasa tupanue kazi yetu ili kujumuisha mamlaka ya juu na mizizi ya juu.

    Hebu tuchunguze msamiati fulani kwanza.

    \(\begin{array}{ll}{\text { We write: }} & {\text { We say: }} \\ {n^{2}} & {n \text { squared }} \\ {n^{3}} & {n \text { cubed }} \\ {n^{4}} & {n \text { to the fourth power }} \\ {n^{5}} & {n \text { to the fifth power }}\end{array}\)

    Neno 'squared' na 'cubed' linatokana na formula kwa eneo la mraba na kiasi cha mchemraba.

    Itakuwa na manufaa kuwa na meza ya nguvu za integers kutoka\(−5\) kwa\(5\). Angalia Kielelezo 8.1.2

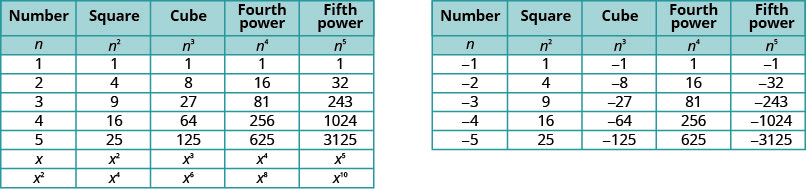
    Takwimu ina meza mbili. Jedwali la kwanza lina safu 9 na nguzo 5. Mstari wa kwanza ni mstari wa kichwa na vichwa â€numberâ €, â € cubeâ €, â € nguvu ya nne €, na â € € nguvu ya tano €. Mstari wa pili una maneno n, n squared, n cubed, n kwa nguvu ya nne, na n kwa nguvu ya tano. Mstari wa tatu una namba 1 katika kila safu. Mstari wa nne una namba 2, 4, 8, 16, 32. Mstari wa tano una namba 3, 9, 27, 81, 243. Mstari wa sita una namba 4, 16, 64, 256, 1024. Mstari wa saba una namba 5, 25, 125 625, 3125. Mstari wa nane una maneno x, x squared, x cubed, x kwa nguvu ya nne, na x kwa nguvu ya tano. Mstari wa mwisho una maneno x mraba, x kwa nguvu ya nne, x kwa nguvu ya sita, x hadi nguvu ya nane, na x hadi nguvu ya kumi. Jedwali la pili lina safu 7 na nguzo 5. Mstari wa kwanza ni mstari wa kichwa na vichwa â€numberâ €, â € cubeâ €, â € nguvu ya nne €, na â € € nguvu ya tano €. Mstari wa pili una maneno n, n squared, n cubed, n kwa nguvu ya nne, na n kwa nguvu ya tano. Mstari wa tatu una namba hasi 1, 1 hasi 1, 1, hasi 1. Mstari wa nne una namba hasi 2, 4, hasi 8, 16, hasi 32. Mstari wa tano una namba hasi 3, 9, hasi 27, 81, hasi 243. Mstari wa sita una namba hasi 4, 16, hasi 64, 256, hasi 1024. Mstari wa mwisho una namba hasi 5, 25, hasi 125, 625, hasi 3125.
    Kielelezo 8.1.2

    Angalia ishara katika meza. Nguvu zote za idadi nzuri ni chanya, bila shaka. Lakini wakati tuna idadi hasi, hata nguvu ni chanya na nguvu isiyo ya kawaida ni hasi. Tutaweza nakala mstari na mamlaka ya\(−2\) kukusaidia kuona hii.

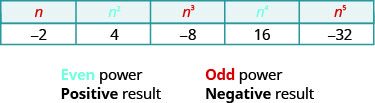
    Picha ina meza yenye safu mbili na nguzo 5. Mstari wa kwanza una maneno n, n squared, n cubed, n kwa nguvu ya nne, na n kwa nguvu ya tano. Mstari wa pili una namba hasi 2, 4, hasi 8, 16, hasi 32. Mishale inaelezea nguzo ya pili na ya nne na studio â€hata nguvu matokeo mazuri â €. Mishale inaelezea nguzo ya kwanza ya tatu na ya tano na studio â € isiyo ya kawaida nguvu matokeo mabaya €.
    Kielelezo 8.1.3

    Sasa tutapanua ufafanuzi wa mizizi ya mraba kwa mizizi ya juu.

    Ufafanuzi\(\PageIndex{3}\): Nth Root of a Number

    Ikiwa\(b^{n}=a\), basi\(b\) ni\(n^{th}\) mzizi wa\(a\).

    \(n^{th}\)mizizi kuu ya\(a\) imeandikwa\(\sqrt[n]{a}\).

    Ya\(n\) inaitwa index ya radical.

    Tu kama sisi kutumia neno 'cubed' kwa ajili ya\(b^{3}\), sisi kutumia neno 'mchemraba mzizi' kwa ajili ya\(\sqrt[3]{a}\).

    Tunaweza kutaja Kielelezo 8.1.2 ili kusaidia kupata mizizi ya juu.

    \(\begin{aligned} 4^{3} &=64 & \sqrt[3]{64}&=4 \\ 3^{4} &=81 & \sqrt[4]{81}&=3 \\(-2)^{5} &=-32 & \sqrt[5]{-32}&=-2 \end{aligned}\)

    Je, tunaweza kuwa na mizizi hata ya idadi hasi? Tunajua kwamba mizizi ya mraba ya namba hasi sio namba halisi. Vile vile ni kweli kwa mizizi yoyote hata. Hata mizizi ya idadi hasi si namba halisi. Mizizi isiyo ya kawaida ya idadi hasi ni namba halisi.

    Mali ya\(\sqrt[n]{a}\)

    Ni\(n\) lini hata idadi na

    • \(a \geq 0\), basi\(\sqrt[n]{a}\) ni namba halisi.
    • \(a<0\), basi\(\sqrt[n]{a}\) si idadi halisi.

    Wakati\(n\) ni idadi isiyo ya kawaida,\(\sqrt[n]{a}\) ni idadi halisi ya maadili yote ya\(a\).

    Tutatumia mali hizi katika mifano miwili ijayo.

    Mfano\(\PageIndex{3}\)

    Kurahisisha:

    1. \(\sqrt[3]{64}\)
    2. \(\sqrt[4]{81}\)
    3. \(\sqrt[5]{32}\)

    Suluhisho:

    a.

    \(\sqrt[3]{64}\)

    Tangu\(4^{3}=64\).

    \(4\)

    b.

    \(\sqrt[4]{81}\)

    Tangu\((3)^{4}=81\).

    \(3\)

    c.

    \(\sqrt[5]{32}\)

    Tangu\((2)^{5}=32\).

    \(2\)

    Zoezi\(\PageIndex{5}\)

    Kurahisisha:

    1. \(\sqrt[3]{27}\)
    2. \(\sqrt[4]{256}\)
    3. \(\sqrt[5]{243}\)
    Jibu
    1. \(3\)
    2. \(4\)
    3. \(3\)
    Zoezi\(\PageIndex{6}\)

    Kurahisisha:

    1. \(\sqrt[3]{1000}\)
    2. \(\sqrt[4]{16}\)
    3. \(\sqrt[5]{243}\)
    Jibu
    1. \(10\)
    2. \(2\)
    3. \(3\)

    Katika mfano huu kuwa macho kwa ishara hasi pamoja na nguvu hata na isiyo ya kawaida.

    Mfano\(\PageIndex{4}\)

    Kurahisisha:

    1. \(\sqrt[3]{-125}\)
    2. \(\sqrt[4]{16}\)
    3. \(\sqrt[5]{-243}\)

    Suluhisho:

    a.

    \(\sqrt[3]{-125}\)

    Tangu\((-5)^{3}=-125\).

    \(-5\)

    b.

    \(\sqrt[4]{16}\)

    Fikiria,\((?)^{4}=-16\). Hakuna idadi halisi iliyofufuliwa kwa nguvu ya nne ni hasi.

    Si idadi halisi.

    c.

    \(\sqrt[5]{-243}\)

    Tangu\((-3)^{5}=-243\).

    \(-3\)

    Zoezi\(\PageIndex{7}\)

    Kurahisisha:

    1. \(\sqrt[3]{-27}\)
    2. \(\sqrt[4]{-256}\)
    3. \(\sqrt[5]{-32}\)
    Jibu
    1. \(-3\)
    2. si kweli
    3. \(-2\)
    Zoezi\(\PageIndex{8}\)

    Kurahisisha:

    1. \(\sqrt[3]{-216}\)
    2. \(\sqrt[4]{-81}\)
    3. \(\sqrt[5]{-1024}\)
    Jibu
    1. \(-6\)
    2. si kweli
    3. \(-4\)

    Makadirio na Mizizi ya

    Tunapoona namba yenye ishara kali, mara nyingi hatufikiri juu ya thamani yake ya namba. Wakati sisi pengine kujua kwamba\(\sqrt{4}=2\), nini ni thamani ya\(\sqrt{21}\) au\(\sqrt[3]{50}\)? Katika hali fulani makadirio ya haraka ni ya maana na kwa wengine ni rahisi kuwa na makadirio ya decimal.

    Ili kupata makadirio ya namba ya mizizi ya mraba, tunatafuta namba kamili za mraba karibu na radicand. Ili kupata makadirio ya\(\sqrt{11}\), tunaona\(11\) ni kati ya namba kamili za mraba\(9\) na\(16\), karibu na\(9\). Mizizi yake ya mraba basi itakuwa kati\(3\) na\(4\), lakini karibu na\(3\).

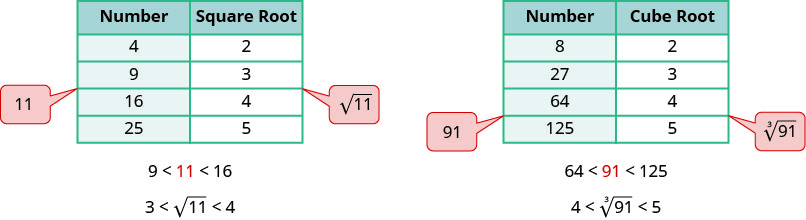
    Takwimu ina meza mbili. Jedwali la kwanza lina safu 5 na nguzo 2. Mstari wa kwanza ni mstari wa kichwa na vichwa â€numberâ € na â €Square Rootâ €. Mstari wa pili una namba 4 na 2. Mstari wa tatu ni 9 na 3. Mstari wa nne ni 16 na 4. Mstari wa mwisho ni 25 na 5. Callout iliyo na namba 11 inaelekezwa kati ya 9 na 16 katika safu ya kwanza. Mwingine callout iliyo na namba mizizi ya mraba ya 11 inaelekezwa kati ya 3 na 4 ya safu ya pili. Chini ya meza ni usawa 9 ni chini ya 11 ni chini ya 16 na 3 ni chini ya mizizi ya mraba ya 11 ni chini ya 4. Jedwali la pili lina safu 5 na nguzo 2. Mstari wa kwanza ni mstari wa kichwa na vichwa â€numberâ € na â € mchemraba Rootâ €. Mstari wa pili una namba 8 na 2. Mstari wa tatu ni 27 na 3. Mstari wa nne ni 64 na 4. Mstari wa mwisho ni 125 na 5. Callout iliyo na namba 91 inaelekezwa kati ya 64 na 125 katika safu ya kwanza. Mwingine callout zenye idadi mchemraba mizizi ya 91 ni moja kwa moja kati ya 4 na 5 ya safu ya pili. Chini ya meza ni usawa 64 ni chini ya 91 ni chini ya 125 na 4 ni chini ya mchemraba mzizi wa 91 ni chini ya 5.
    Kielelezo 8.1.4

    Vile vile, kukadiria\(\sqrt[3]{91}\), tunaona\(91\) ni kati ya namba kamili mchemraba\(64\) na\(125\). Mizizi ya mchemraba basi itakuwa kati\(4\) na\(5\).

    Mfano\(\PageIndex{5}\)

    Tathmini kila mizizi kati ya namba mbili za mfululizo:

    1. \(\sqrt{105}\)
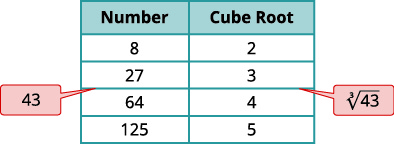
    2. \(\sqrt[3]{43}\)

    Suluhisho:

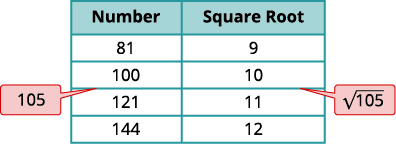
    Fikiria idadi kamili ya mraba karibu na\(105\). Fanya meza ndogo ya mraba huu kamili na mizizi yao ya mraba.

    Jedwali 8.1.1
      \(\sqrt{105}\)
      .
    Machapisho\(105\) kati ya mraba mbili mfululizo kamili. \(100<\color{red}105 \color{black} <121\)
    \(\sqrt{105}\)ni kati ya mizizi yao ya mraba. \(10< \color{red}\sqrt{105}< \color{black}11\)

    b Vile vile sisi Machapisho\(43\) kati ya namba mbili kamili mchemraba.

    Jedwali 8.1.2
      \(\sqrt[3]{43}\)
      .
    Machapisho\(43\) kati ya cubes mbili mfululizo kamili. .
    \(\sqrt[3]{43}\)ni kati ya mizizi yao mchemraba. .
    Zoezi\(\PageIndex{9}\)

    Tathmini kila mizizi kati ya namba mbili za mfululizo:

    1. \(\sqrt{38}\)
    2. \(\sqrt[3]{93}\)
    Jibu
    1. \(6<\sqrt{38}<7\)
    2. \(4<\sqrt[3]{93}<5\)
    Zoezi\(\PageIndex{10}\)

    Tathmini kila mizizi kati ya namba mbili za mfululizo:

    1. \(\sqrt{84}\)
    2. \(\sqrt[3]{152}\)
    Jibu
    1. \(9<\sqrt{84}<10\)
    2. \(5<\sqrt[3]{152}<6\)

    Kuna mbinu za hisabati kwa takriban mizizi ya mraba, lakini siku hizi watu wengi hutumia calculator kupata mizizi ya mraba. Ili kupata mizizi ya mraba utatumia\(\sqrt{x}\) ufunguo kwenye calculator yako. Ili kupata mizizi ya mchemraba, au mizizi yoyote yenye index ya juu, utatumia\(\sqrt[y]{x}\) ufunguo.

    Unapotumia funguo hizi, unapata thamani ya takriban. Ni makadirio, sahihi na idadi ya tarakimu inavyoonekana kwenye kuonyesha calculator yako ya. ishara kwa makadirio ni\(≈\) na ni kusoma 'takriban '.

    Tuseme calculator yako ina kuonyesha\(10\) tarakimu. Ungependa kuona kwamba

    \(\sqrt{5} \approx 2.236067978\)mviringo kwa maeneo mawili decimal ni\(\sqrt{5} \approx 2.24\)

    \(\sqrt[4]{93} \approx 3.105422799\)mviringo kwa maeneo mawili decimal ni\(\sqrt[4]{93} \approx 3.11\)

    Je, tunajua maadili haya ni makadirio na si maadili halisi? Angalia nini kinatokea wakati sisi mraba yao:

    \(\begin{aligned}(2.236067978)^{2} &=5.000000002 &(3.105422799)^{4}&=92.999999991 \\(2.24)^{2} &=5.0176 & (3.11)^{4}&=93.54951841 \end{aligned}\)

    Mraba yao ni karibu na\(5\), lakini si sawa sawa na\(5\). Mamlaka ya nne ni karibu\(93\), lakini si sawa na\(93\).

    Mfano\(\PageIndex{6}\)

    Pande zote kwa maeneo mawili ya decimal:

    1. \(\sqrt{17}\)
    2. \(\sqrt[3]{49}\)
    3. \(\sqrt[4]{51}\)

    Suluhisho:

    a.

    \(\sqrt{17}\)

    Tumia ufunguo wa mizizi ya mraba ya calculator.

    \(4.123105626 \dots\)

    Pande zote kwa maeneo mawili ya decimal.

    \(4.12\)

    \(\sqrt{17} \approx 4.12\)

    b.

    \(\sqrt[3]{49}\)

    Tumia\(\sqrt[y]{x}\) ufunguo wa calculator.

    \(3.659305710 \ldots\)

    Pande zote kwa maeneo mawili ya decimal.

    \(3.66\)

    \(\sqrt[3]{49} \approx 3.66\)

    c.

    \(\sqrt[4]{51}\)

    Tumia\(\sqrt[y]{x}\) ufunguo wa calculator.

    \(2.6723451177 \ldots\)

    Pande zote kwa maeneo mawili ya decimal.

    \(2.67\)

    \(\sqrt[4]{51} \approx 2.67\)

    Zoezi\(\PageIndex{11}\)

    Pande zote kwa maeneo mawili ya decimal:

    1. \(\sqrt{11}\)
    2. \(\sqrt[3]{71}\)
    3. \(\sqrt[4]{127}\)
    Jibu
    1. \(\approx 3.32\)
    2. \(\approx 4.14\)
    3. \(\approx 3.36\)
    Zoezi\(\PageIndex{12}\)

    Pande zote kwa maeneo mawili ya decimal:

    1. \(\sqrt{13}\)
    2. \(\sqrt[3]{84}\)
    3. \(\sqrt[4]{98}\)
    Jibu
    1. \(\approx 3.61\)
    2. \(\approx 4.38\)
    3. \(\approx 3.15\)

    Punguza Maneno ya kutofautiana na Mizizi

    Mzizi usio wa kawaida wa namba unaweza kuwa chanya au hasi. Kwa mfano,

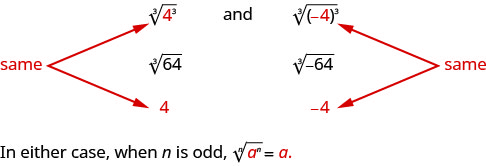
    Maneno matatu sawa yameandikwa: mizizi ya mchemraba wa cubed 4, mizizi ya mchemraba wa 64, na 4. Kuna mishale akizungumzia 4 kwamba ni cubed katika kujieleza kwanza na 4 katika kujieleza mwisho lebo yao kama â € sameâ €. Maneno matatu sawa pia yameandikwa: mizizi ya mchemraba wa wingi hasi 4 katika mabano cubed, mizizi ya mchemraba wa hasi 64, na hasi 4. 4 hasi katika kujieleza kwanza na hasi 4 katika kujieleza mwisho ni kinachoitwa kama â € sameâ €.
    Kielelezo 8.1.13

    Lakini vipi kuhusu mizizi hata? Tunataka mizizi kuu, hivyo\(\sqrt[4]{625}=5\).

    Lakini taarifa,

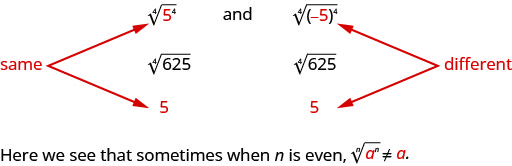
    Maneno matatu sawa yameandikwa: mizizi ya nne ya wingi 5 hadi nguvu ya nne katika mabano, mizizi ya nne ya 625, na 5. Kuna mishale akizungumzia 5 katika kujieleza kwanza na 5 katika kujieleza mwisho lebo yao kama â € sameâ €. Maneno matatu sawa pia yameandikwa: mizizi ya nne ya wingi hasi 5 katika mabano hadi nguvu ya nne katika mabano, mizizi ya nne ya 625, na 5. 5 hasi katika kujieleza kwanza na 5 katika kujieleza mwisho ni kinachoitwa kama kuwa â € € differentâ €.
    Kielelezo 8.1.14

    Tunawezaje kuhakikisha mizizi ya nne ya\(−5\) kukulia kwa nguvu ya nne ni\(5\)? Tunaweza kutumia thamani kamili. \(|−5|=5\). Kwa hiyo tunasema kwamba wakati\(n\) ni hata\(\sqrt[n]{a^{n}}=|a|\). Hii inathibitisha mizizi kuu ni chanya.

    Ufafanuzi\(\PageIndex{4}\): Simplifying Odd and Even Roots

    Kwa integer yoyote\(n\geq 2\),

    wakati index\(n\) ni isiyo ya kawaida\(\sqrt[n]{a^{n}}=a\)

    wakati index\(n\) ni hata\(\sqrt[n]{a^{n}}=|a|\)

    Ni lazima kutumia thamani kamili ishara wakati sisi kuchukua hata mizizi ya kujieleza na variable katika radical.

    Mfano\(\PageIndex{7}\)

    Kurahisisha:

    1. \(\sqrt{x^{2}}\)
    2. \(\sqrt[3]{n^{3}}\)
    3. \(\sqrt[4]{p^{4}}\)
    4. \(\sqrt[5]{y^{5}}\)

    Suluhisho:

    Tunatumia thamani kamili ili uhakikishe kupata mizizi nzuri.

    \(\sqrt{x^{2}}\)

    Tangu index\(n\) ni hata,\(\sqrt[n]{a^{n}}=|a|\).

    b Hii ni mizizi isiyo ya kawaida ya indexed kwa hiyo hakuna haja ya ishara ya thamani kamili.

    \(\sqrt[3]{m^{3}}\)

    Tangu index\(n\) ni isiyo ya kawaida,\(\sqrt[n]{a^{n}}=a\).

    \(m\)

    c.

    \(\sqrt[4]{p^{4}}\)

    Tangu index\(n\) ni hata\(\sqrt[n]{a^{n}}=|a|\).

    \(|p|\)

    d.

    \(\sqrt[5]{y^{5}}\)

    Tangu index\(n\) ni isiyo ya kawaida,\(\sqrt[n]{a^{n}}=a\).

    \(y\)

    Zoezi\(\PageIndex{13}\)

    Kurahisisha:

    1. \(\sqrt{b^{2}}\)
    2. \(\sqrt[3]{w^{3}}\)
    3. \(\sqrt[4]{m^{4}}\)
    4. \(\sqrt[5]{q^{5}}\)
    Jibu
    1. \(|b|\)
    2. \(w\)
    3. \(|m|\)
    4. \(q\)
    Zoezi\(\PageIndex{14}\)

    Kurahisisha:

    1. \(\sqrt{y^{2}}\)
    2. \(\sqrt[3]{p^{3}}\)
    3. \(\sqrt[4]{z^{4}}\)
    4. \(\sqrt[5]{q^{5}}\)
    Jibu
    1. \(|y|\)
    2. \(p\)
    3. \(|z|\)
    4. \(q\)

    Nini kuhusu mizizi ya mraba ya mamlaka ya juu ya vigezo? Nguvu Mali ya Exponents anasema\(\left(a^{m}\right)^{n}=a^{m \cdot n}\). Hivyo kama sisi mraba\(a^{m}\), exponent itakuwa\(2m\).

    \(\left(a^{m}\right)^{2}=a^{2 m}\)

    Kuangalia sasa kwenye mizizi ya mraba.

    \(\sqrt{a^{2 m}}\)

    Tangu\(\left(a^{m}\right)^{2}=a^{2 m}\).

    \(\sqrt{\left(a^{m}\right)^{2}}\)

    Tangu\(n\) ni hata\(\sqrt[n]{a^{n}}=|a|\).

    \(\left|a^{m}\right|\)

    Hivyo\(\sqrt{a^{2 m}}=\left|a^{m}\right|\).

    Tunatumia dhana hii katika mfano unaofuata.

    Mfano\(\PageIndex{8}\)

    Kurahisisha:

    1. \(\sqrt{x^{6}}\)
    2. \(\sqrt{y^{16}}\)

    Suluhisho:

    a.

    \(\sqrt{x^{6}}\)

    Tangu\(\left(x^{3}\right)^{2}=x^{6}\).

    \(\sqrt{\left(x^{3}\right)^{2}}\)

    Tangu index\(n\) ni hata\(\sqrt{a^{n}}=|a|\).

    \(\left|x^{3}\right|\)

    b.

    \(\sqrt{y^{16}}\)

    Tangu\(\left(y^{8}\right)^{2}=y^{16}\).

    \(\sqrt{\left(y^{8}\right)^{2}}\)

    Tangu index\(n\) ni hata\(\sqrt[n]{a^{n}}=|a|\).

    \(y^{8}\)

    Katika kesi hii, ishara ya thamani kamili haihitajiki kama\(y^{8}\) ilivyo chanya.

    Zoezi\(\PageIndex{15}\)

    Kurahisisha:

    1. \(\sqrt{y^{18}}\)
    2. \(\sqrt{z^{12}}\)
    Jibu
    1. \(|y^{9}|\)
    2. \(z^{6}\)
    Zoezi\(\PageIndex{16}\)

    Kurahisisha:

    1. \(\sqrt{m^{4}}\)
    2. \(\sqrt{b^{10}}\)
    Jibu
    1. \(m^{2}\)
    2. \(|b^{5}|\)

    Mfano unaofuata unatumia wazo sawa kwa mizizi ya juu.

    Mfano\(\PageIndex{9}\)

    Kurahisisha:

    1. \(\sqrt[3]{y^{18}}\)
    2. \(\sqrt[4]{z^{8}}\)

    Suluhisho:

    a.

    \(\sqrt[3]{y^{18}}\)

    Tangu\(\left(y^{6}\right)^{3}=y^{18}\).

    \(\sqrt[3]{\left(y^{6}\right)^{3}}\)

    Kwa kuwa\(n\) ni isiyo ya kawaida,\(\sqrt[n]{a^{n}}=a\).

    \(y^{6}\)

    b.

    \(\sqrt[4]{z^{8}}\)

    Tangu\(\left(z^{2}\right)^{4}=z^{8}\).

    \(\sqrt[4]{\left(z^{2}\right)^{4}}\)

    Kwa kuwa\(z^{2}\) ni chanya, hatuhitaji ishara ya thamani kamili.

    \(z^{2}\)

    Zoezi\(\PageIndex{17}\)

    Kurahisisha:

    1. \(\sqrt[4]{u^{12}}\)
    2. \(\sqrt[3]{v^{15}}\)
    Jibu
    1. \(|u^{3}|\)
    2. \(v^{5}\)
    Zoezi\(\PageIndex{18}\)

    Kurahisisha:

    1. \(\sqrt[5]{c^{20}}\)
    2. \(\sqrt[6]{d^{24}}\)
    Jibu
    1. \(c^{4}\)
    2. \(d^{4}\)

    Katika mfano unaofuata, sasa tuna mgawo mbele ya kutofautiana. Dhana\(\sqrt{a^{2 m}}=\left|a^{m}\right|\) inafanya kazi kwa njia sawa.

    \(\sqrt{16 r^{22}}=4\left|r^{11}\right|\)kwa sababu\(\left(4 r^{11}\right)^{2}=16 r^{22}\).

    Lakini taarifa\(\sqrt{25 u^{8}}=5 u^{4}\) na hakuna ishara ya thamani kamili inahitajika kama\(u^{4}\) ilivyo daima chanya.

    Mfano\(\PageIndex{10}\)

    Kurahisisha:

    1. \(\sqrt{16 n^{2}}\)
    2. \(-\sqrt{81 c^{2}}\)

    Suluhisho:

    a.

    \(\sqrt{16 n^{2}}\)

    Tangu\((4 n)^{2}=16 n^{2}\).

    \(\sqrt{(4 n)^{2}}\)

    Tangu index\(n\) ni hata\(\sqrt[n]{a^{n}}=|a|\).

    \(4|n|\)

    b.

    \(-\sqrt{81 c^{2}}\)

    Tangu\((9 c)^{2}=81 c^{2}\).

    \(-\sqrt{(9 c)^{2}}\)

    Tangu index\(n\) ni hata\(\sqrt[n]{a^{n}}=|a|\).

    \(-9|c|\)

    Zoezi\(\PageIndex{19}\)

    Kurahisisha:

    1. \(\sqrt{64 x^{2}}\)
    2. \(-\sqrt{100 p^{2}}\)
    Jibu
    1. \(8|x|\)
    2. \(-10|p|\)
    Zoezi\(\PageIndex{20}\)

    Kurahisisha:

    1. \(\sqrt{169 y^{2}}\)
    2. \(-\sqrt{121 y^{2}}\)
    Jibu
    1. \(13|y|\)
    2. \(-11|y|\)

    Mfano huu tu inachukua wazo mbali kama ina mizizi ya index ya juu.

    Mfano\(\PageIndex{11}\)

    Kurahisisha:

    1. \(\sqrt[3]{64 p^{6}}\)
    2. \(\sqrt[4]{16 q^{12}}\)

    Suluhisho:

    a.

    \(\sqrt[3]{64 p^{6}}\)

    Andika upya\(64p^{6}\) kama\(\left(4 p^{2}\right)^{3}\).

    \(\sqrt[3]{\left(4 p^{2}\right)^{3}}\)

    Chukua mizizi ya mchemraba.

    \(4p^{2}\)

    b.

    \(\sqrt[4]{16 q^{12}}\)

    Andika upya radicand kama nguvu ya nne.

    \(\sqrt[4]{\left(2 q^{3}\right)^{4}}\)

    Chukua mizizi ya nne.

    \(2|q^{3}|\)

    Zoezi\(\PageIndex{21}\)

    Kurahisisha:

    1. \(\sqrt[3]{27 x^{27}}\)
    2. \(\sqrt[4]{81 q^{28}}\)
    Jibu
    1. \(3x^{9}\)
    2. \(3|q^{7}|\)
    Zoezi\(\PageIndex{22}\)

    Kurahisisha:

    1. \(\sqrt[3]{125 q^{9}}\)
    2. \(\sqrt[5]{243 q^{25}}\)
    Jibu
    1. \(5p^{3}\)
    2. \(3q^{5}\)

    Mifano inayofuata ina vigezo viwili.

    Mfano\(\PageIndex{12}\)

    Kurahisisha:

    1. \(\sqrt{36 x^{2} y^{2}}\)
    2. \(\sqrt{121 a^{6} b^{8}}\)
    3. \(\sqrt[3]{64 p^{63} q^{9}}\)

    Suluhisho:

    a.

    \(\sqrt{36 x^{2} y^{2}}\)

    Tangu\((6 x y)^{2}=36 x^{2} y^{2}\)

    \(\sqrt{(6 x y)^{2}}\)

    Chukua mizizi ya mraba.

    \(6|xy|\)

    b.

    \(\sqrt{121 a^{6} b^{8}}\)

    Tangu\(\left(11 a^{3} b^{4}\right)^{2}=121 a^{6} b^{8}\)

    \(\sqrt{\left(11 a^{3} b^{4}\right)^{2}}\)

    Chukua mizizi ya mraba.

    \(11\left|a^{3}\right| b^{4}\)

    c.

    \(\sqrt[3]{64 p^{63} q^{9}}\)

    Tangu\(\left(4 p^{21} q^{3}\right)^{3}=64 p^{63} q^{9}\)

    \(\sqrt[3]{\left(4 p^{21} q^{3}\right)^{3}}\)

    Chukua mizizi ya mchemraba.

    \(4p^{21}q^{3}\)

    Zoezi\(\PageIndex{23}\)

    Kurahisisha:

    1. \(\sqrt{100 a^{2} b^{2}}\)
    2. \(\sqrt{144 p^{12} q^{20}}\)
    3. \(\sqrt[3]{8 x^{30} y^{12}}\)
    Jibu
    1. \(10|ab|\)
    2. \(12p^{6}q^{10}\)
    3. \(2x^{10}y^{4}\)
    Zoezi\(\PageIndex{24}\)

    Kurahisisha:

    1. \(\sqrt{225 m^{2} n^{2}}\)
    2. \(\sqrt{169 x^{10} y^{14}}\)
    3. \(\sqrt[3]{27 w^{36} z^{15}}\)
    Jibu
    1. \(15|mn|\)
    2. \(13\left|x^{5} y^{7}\right|\)
    3. \(3w^{12}z^{5}\)

    Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na maneno rahisi na mizizi.

    • Kurahisisha Vigezo Maonyesho na Mizizi kwa kutumia Maadili kamili

    Dhana muhimu

    • Mizizi ya Mizizi ya mraba
      • \(\sqrt{m}\)ni kusoma 'mizizi mraba ya\(m\) '
      • Ikiwa\(n^{2}=m\), basi\(n=\sqrt{m}\), kwa\(n≥0\).
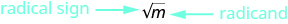
        Picha inaonyesha m ya kutofautiana ndani ya ishara ya mizizi ya mraba. Ishara ni mstari unaoendelea juu upande wa kushoto halafu bapa juu ya variable. Ishara inaitwa “ishara kali”. M ya kutofautiana inaitwa “radicand”.
        Kielelezo 8.1.1
      • Mizizi ya mraba ya\(m\)\(\sqrt{m}\),, ni idadi nzuri ambayo mraba ni\(m\).
    • Katika Mizizi ya Idadi
      • Ikiwa\(b^{n}=a\), basi\(b\) ni\(n^{th}\) mzizi wa\(a\).
      • \(n^{th}\)mizizi kuu ya\(a\) imeandikwa\(\sqrt[n]{a}\).
      • \(n\)inaitwa index ya radical.
    • Mali ya\(\sqrt[n]{a}\)
      • Ni\(n\) lini hata idadi na
        • \(a≥0\), basi\(\sqrt[n]{a}\) ni idadi halisi
        • \(a<0\), basi\(\sqrt[n]{a}\) si idadi halisi
      • Wakati\(n\) ni idadi isiyo ya kawaida,\(\sqrt[n]{a}\) ni idadi halisi kwa maadili yote ya\(a\).
    • Kurahisisha Odd na Hata mizizi
      • Kwa integer yoyote\(n≥2\),
        • wakati\(n\) ni isiyo ya kawaida\(\sqrt[n]{a^{n}}=a\)
        • \(n\)lini ni hata\(\sqrt[n]{a^{n}}=|a|\)
      • Ni lazima kutumia thamani kamili ishara wakati sisi kuchukua hata mizizi ya kujieleza na variable katika radical.

    faharasa

    mraba wa idadi
    Ikiwa\(n^{2}=m\), basi\(m\) ni mraba wa\(n\).
    mizizi ya mraba ya idadi
    Ikiwa\(n^{2}=m\), basi\(n\) ni mizizi ya mraba ya\(m\).