Skip to main content
Global

6.2E: Mazoezi

  1. Last updated
  2. Save as PDF
  • Page ID
    176132

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mazoezi hufanya kamili

    Pata sababu kubwa ya kawaida ya maneno mawili au Zaidi

    Katika mazoezi yafuatayo, pata sababu kubwa zaidi ya kawaida.

    1. \(10p^3q,12pq^2\)

    Jibu

    \(2pq\)

    2. \(8a^2b^3,10ab^2\)

    3. \(12m^2n^3,30m^5n^3\)

    Jibu

    \(6m^2n^3\)

    4. \(28x^2y^4,42x^4y^4\)

    5. \(10a^3,12a^2,14a\)

    Jibu

    \(2a\)

    6. \(20y^3,28y^2,40y\)

    7. \(35x^3y^2,10x^4y,5x^5y^3\)

    Jibu

    \(5x^3y\)

    8. \(27p^2q^3,45p^3q^4,9p^4q^3\)

    Sababu ya Sababu kuu ya kawaida kutoka kwa Polynomial

    Katika mazoezi yafuatayo, fikiria sababu kubwa zaidi kutoka kwa kila polynomial.

    9. \(6m+9\)

    Jibu

    \(3(2m+3)\)

    10. \(14p+35\)

    11. \(9n−63\)

    Jibu

    \(9(n−7)\)

    12. \(45b−18\)

    13. \(3x^2+6x−9\)

    Jibu

    \(3(x^2+2x−3)\)

    14. \(4y^2+8y−4\)

    15. \(8p^2+4p+2\)

    Jibu

    \(2(4p^2+2p+1)\)

    16. \(10q^2+14q+20\)

    17. \(8y^3+16y^2\)

    Jibu

    \(8y^2(y+2)\)

    18. \(12x^3−10x\)

    19. \(5x^3−15x^2+20x\)

    Jibu

    \(5x(x^2−3x+4)\)

    20. \(8m^2−40m+16\)

    21. \(24x^3−12x^2+15x\)

    Jibu

    \(3x(8x^2−4x+5)\)

    22. \(24y^3−18y^2−30y\)

    23. \(12xy^2+18x^2y^2−30y^3\)

    Jibu

    \(6y^2(2x+3x^2−5y)\)

    24. \(21pq^2+35p^2q^2−28q^3\)

    25. \(20x^3y−4x^2y^2+12xy^3\)

    Jibu

    \(4xy(5x^2−xy+3y^2)\)

    26. \(24a^3b+6a^2b^2−18ab^3\)

    27. \(−2x−4\)

    Jibu

    \(−2(x+4)\)

    28. \(−3b+12\)

    29. \(−2x^3+18x^2−8x\)

    Jibu

    \(−2x(x^2−9x+4)\)

    30. \(−5y^3+35y^2−15y\)

    31. \(−4p^3q−12p^2q^2+16pq^2\)

    Jibu

    \(−4pq(p^2+3pq−4q)\)

    32. \(−6a^3b−12a^2b^2+18ab^2\)

    33. \(5x(x+1)+3(x+1)\)

    Jibu

    \((x+1)(5x+3)\)

    34. \(2x(x−1)+9(x−1)\)

    35. \(3b(b−2)−13(b−2)\)

    Jibu

    \((b−2)(3b−13)\)

    36. \(6m(m−5)−7(m−5)\)

    Kipengele kwa Kundi

    Katika mazoezi yafuatayo, sababu kwa kikundi.

    37. \(ab+5a+3b+15\)

    Jibu

    \((b+5)(a+3)\)

    38. \(cd+6c+4d+24\)

    39. \(8y^2+y+40y+5\)

    Jibu

    \((y+5)(8y+1)\)

    40. \(6y^2+7y+24y+28\)

    41. \(uv−9u+2v−18\)

    Jibu

    \((u+2)(v−9)\)

    42. \(pq−10p+8q−80\)

    43. \(u^2−u+6u−6\)

    Jibu

    \((u−1)(u+6)\)

    44. \(x^2−x+4x−4\)

    45. \(9p^2−15p+12p−20\)

    Jibu

    \((3p−5)(3p+4)\)

    46. \(16q^2+20q−28q−35\)

    47. \(mn−6m−4n+24\)

    Jibu

    \((n−6)(m−4)\)

    48. \(r^2−3r−r+3\)

    49. \(2x^2−14x−5x+35\)

    Jibu

    \((x−7)(2x−5)\)

    50. \(4x^2−36x−3x+27\)

    Mazoezi ya mchanganyiko

    Katika mazoezi yafuatayo, sababu.

    51. \(−18xy^2−27x^2y\)

    Jibu

    \(−9xy(3x+2y)\)

    52. \(−4x^3y^5−x^2y^3+12xy^4\)

    53. \(3x^3−7x^2+6x−14\)

    Jibu

    \((x^2+2)(3x−7)\)

    54. \(x^3+x^2−x−1\)

    55. \(x^2+xy+5x+5y\)

    Jibu

    \((x+y)(x+5)\)

    56. \(5x^3−3x^2+5x−3\)

    Mazoezi ya kuandika

    57. Ina maana gani kusema polynomial iko katika fomu iliyosababishwa?

    Jibu

    Majibu yatatofautiana.

    58. Je, wewe kuangalia matokeo baada ya factoring polynomial?

    59. Sababu kubwa ya kawaida ya\(36\) na\(60\) ni\(12\). Eleza nini hii inamaanisha.

    Jibu

    Majibu yatatofautiana.

    60. ni GCF ya nini\(y^4,\space y^5\), na\(y^{10}\)? Andika kanuni ya jumla kwamba atakwambia jinsi ya kupata GCF ya\(y^a,\space y^b\), na\(y^c\).

    Self Check

    ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

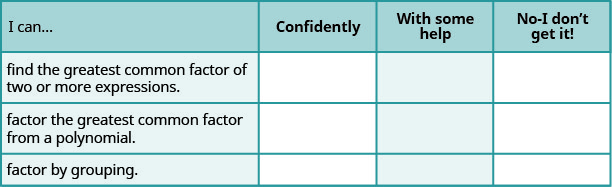
    Jedwali hili lina nguzo 4, safu 3 na mstari wa kichwa. Mstari wa kichwa huandika kila safu ninayoweza, kwa ujasiri, kwa msaada fulani na hapana siipate. Safu ya kwanza ina kauli zifuatazo: tafuta sababu kubwa zaidi ya maneno 2 au zaidi, sababu ya sababu kubwa zaidi kutoka kwa polynomial, sababu kwa kikundi. Nguzo zilizobaki ni tupu.

    ⓑ Kama wengi wa hundi yako walikuwa:

    ... kwa ujasiri. Hongera! Umefanikiwa malengo yako katika sehemu hii! Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum!

    ... kwa msaada fulani. Hii lazima kushughulikiwa haraka kama mada wewe si bwana kuwa mashimo katika barabara yako ya mafanikio. Math ni mtiririko - kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha kuwa na msingi imara kabla ya kuendelea. Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?

    ... hapana - Siipati! Hii ni muhimu na haipaswi kupuuza. Unahitaji kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo ili kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.