6.3: Sababu Trinomials

Last updated
Save as PDF

Page ID: 176050

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Factor trinomials ya fomu$x^2+bx+c$
Vipengele vya trinomials ya fomu kwa$ax^2+bx+c$ kutumia jaribio na hitilafu
Factor trinomials ya fomu$ax^2+bx+c$ kwa kutumia '$ac$' njia
Sababu ya kutumia badala

Kabla ya kuanza, fanya jaribio hili la utayari.

Kupata mambo yote ya 72.
Ikiwa umekosa tatizo hili, tathmini [kiungo].
Pata bidhaa:$(3y+4)(2y+5)$.
Ikiwa umekosa tatizo hili, tathmini [kiungo].
Kurahisisha:$−9(6);\space −9(−6)$.
Ikiwa umekosa tatizo hili, tathmini [kiungo].

Sababu Trinomials ya Fomu$x^2+bx+c$

Tayari umejifunza jinsi ya kuzidisha binomials kwa kutumia FOIL. Sasa utahitaji “kurekebisha” kuzidisha hii. Ili kuzingatia njia ya trinomial kuanza na bidhaa, na kuishia na mambo.

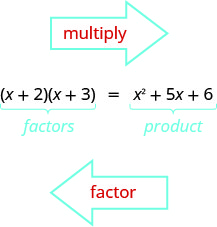
$Kielelezo inaonyesha equation wazi mabano x plus 2 karibu mabano wazi x plus 3 karibu mabano sawa x squared pamoja 5 x plus 6. Upande wa kushoto wa equation ni kinachoitwa sababu na haki ni kinachoitwa bidhaa. mshale akizungumzia haki ni kinachoitwa kuzidisha. mshale akizungumzia kushoto ni kinachoitwa sababu.$

Ili kujua jinsi tutaweza kuzingatia trinomial ya fomu$x^2+bx+c$, kama vile$x^2+5x+6$ na kuzingatia$(x+2)(x+3)$, hebu tuanze na binomials mbili za jumla za fomu$(x+m)$ na$(x+n)$.

	$(x+m)(x+n)$
Foil kupata bidhaa.	$x^{2}+m x+n x+m n$
Factor GCF kutoka suala la kati.	$x^{2}+(m+n) x+m n$
Trinomial yetu ni ya fomu$x^2+bx+c$.	$\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}$

Hii inatuambia kwamba kwa sababu ya trinomial ya fomu$x^2+bx+c$, tunahitaji mambo mawili$(x+m)$ na$(x+n)$ ambapo namba mbili$m$ na$n$ kuzidisha$c$ na kuongeza$b$.

Mfano$\PageIndex{1}$: How to Factor a Trinomial of the form $x^2+bx+c$

Sababu:$x^2+11x+24$.

Jibu: $Hatua ya 1 ni kuandika sababu za x squared plus 11x plus 24 kama binomials mbili na maneno ya kwanza x Andika seti mbili za mabano na kuweka x kama muda wa kwanza.$ $Hatua ya 2 ni kupata namba mbili m na n kwamba kuzidisha kwa c, m mara n ni c na kuongeza b, m plus n ni b Hivyo, kupata namba mbili kwamba kuzidisha kwa 24 na kuongeza 11. Mambo ya 24 ni 1 na 24, 2 na 12, 3 na 8, 4 na 6. Jumla ya mambo: 1 pamoja na 24 ni 25, 2 pamoja na 12 ni 14, 3 pamoja na 8 ni 11 na 4 pamoja na 6 ni 10.$ $Hatua ya 3 ni kutumia m na n, katika kesi hii, 3 na 8, kama masharti ya mwisho ya binomials. Kwa hiyo tunapata mabano ya wazi x pamoja na 3 mabano ya karibu: kufungua mabano x pamoja na 8 mabano ya karibu.$ $Hatua ya 4 ni kuangalia kwa kuzidisha mambo ya kupata polynomial ya awali.$

Mfano$\PageIndex{2}$

Sababu:$q^2+10q+24$.

Jibu: $(q+4)(q+6)$

Mfano$\PageIndex{3}$

Sababu:$t^2+14t+24$.

Jibu: $(t+2)(t+12)$

Hebu tufupishe muhtasari hatua tulizotumia kupata mambo.

Andika mambo kama binomials mbili na maneno ya kwanza x. $\quad \begin{array} {l} x^2+bx+c \\ (x\quad)(x\quad) \end{array} $
Kupata namba mbili$m$ na$n$ kwamba
- kuzidisha kwa$c$,$m·n=c$
- ongeza kwa$b$,$m+n=b$
Tumia$m$ na$n$ kama masharti ya mwisho ya mambo. $\quad (x+m)(x+n)$
Angalia kwa kuzidisha mambo.

Katika mfano wa kwanza, maneno yote katika trinomial yalikuwa chanya. Ni nini kinachotokea wakati kuna maneno mabaya? Naam, inategemea muda gani ni hasi. Hebu tuangalie kwanza katika trinomials na tu ya muda wa kati hasi.

Je, unapataje bidhaa nzuri na jumla hasi? Tunatumia namba mbili hasi.

Mfano$\PageIndex{4}$

Sababu:$y^2−11y+28$.

Jibu

Tena, kwa chanya mrefu mwisho$28$,, na hasi katikati mrefu$−11y$, tunahitaji sababu mbili hasi. Pata namba mbili zinazozidisha$28$ na kuongeza$−11$.
$\begin{array} {ll} &y^2−11y+28 \\ \text{Write the factors as two binomials with first terms }y. &( y \quad )( y \quad ) \\ \text{Find two numbers that: multiply to }28\text{ and add to }−11.\end{array}$

Mambo ya$28$	Jumla ya mambo
\ (28\)” data-valign="top">$−1,\space −28$ $−2,\space −14$ $−4,\space −7$	$−1+(−28)=−29$ $−2+(−14)=−16$ $−4+(−7)=−11^∗$

$\begin{array} {ll} \text{Use }−4,\space −7\text{ as the last terms of the binomials.} &(y−4)(y−7) \\ \text{Check:} & \\ \hspace{30mm} (y−4)(y−7) & \\ \hspace{25mm} y^2−7y−4y+28 & \\ \hspace{30mm} y^2−11y+28\checkmark & \end{array} $

Mfano$\PageIndex{5}$

Sababu:$u^2−9u+18$.

Jibu: $(u−3)(u−6)$

Mfano$\PageIndex{6}$

Sababu:$y^2−16y+63$.

Jibu: $(y−7)(y−9)$

Sasa, vipi ikiwa muda wa mwisho katika trinomial ni hasi? Fikiria kuhusu FOIL. Muda wa mwisho ni bidhaa ya maneno ya mwisho katika binomials mbili. Matokeo ya bidhaa hasi kutokana na kuzidisha namba mbili na ishara tofauti. Unapaswa kuwa makini sana kuchagua mambo ili kuhakikisha unapata ishara sahihi kwa muda wa kati, pia.

Je, unapataje bidhaa hasi na jumla chanya? Tunatumia nambari moja nzuri na moja hasi.

Wakati sisi sababu trinomials, ni lazima kuwa na maneno yaliyoandikwa katika kushuka mpango-ili kutoka shahada ya juu hadi shahada ya chini.

Mfano$\PageIndex{7}$

Sababu:$2x+x^2−48$.

Jibu

$\begin{array} {ll} &2x+x^2−48 \\ \text{First we put the terms in decreasing degree order.} &x^2+2x−48 \\ \text{Factors will be two binomials with first terms }x. &(x\quad)(x\quad) \end{array} $

Mambo ya -48—48	Jumla ya mambo
$−1,\space 48$ $−2,\space 24$ $−3,\space 16$ $−4,\space 12$ $−6,\space 8$	$−1+48=47$ $−2+24=22$ $−3+16=13$ $−4+12=8$ $−6+8=2^∗$

$\begin{array} {ll} \text{Use }−6,\space 8\text{ as the last terms of the binomials.} &(x−6)(x+8) \\ \text{Check:} & \\ \hspace{30mm} (x−6)(x+8) & \\ \hspace{25mm} x^2−6q+8q−48 & \\ \hspace{30mm} x^2+2x−48\checkmark & \end{array} $

Mfano$\PageIndex{8}$

Sababu:$9m+m^2+18$.

Jibu: $(m+3)(m+6)$

Mfano$\PageIndex{9}$

Sababu:$−7n+12+n^2$.

Jibu: $(n−3)(n−4)$

Wakati mwingine itabidi sababu trinomials ya fomu$x^2+bxy+cy^2$ na vigezo mbili, kama vile$x^2+12xy+36y^2$. Neno la kwanza$x^2$,, ni bidhaa ya maneno ya kwanza ya mambo ya binomial,$x·x$. Ya$y^2$ katika muda wa mwisho ina maana kwamba maneno ya pili ya mambo ya binomial lazima kila mmoja yana$y$. Ili kupata coefficients$b$ na$c$, unatumia mchakato huo muhtasari katika Jinsi ya Factor trinomials.

Mfano$\PageIndex{10}$

Sababu:$r^2−8rs−9s^2$.

Jibu

Tunahitaji$r$ katika muda wa kwanza wa kila binomial na$s$ katika muda wa pili. Muda wa mwisho wa trinomial ni hasi, hivyo sababu lazima ziwe na ishara tofauti.
$\begin{array} {ll} &r^2−8rs−9s^2 \\ \text{Note that the first terms are }r,\text{last terms contain }s. &(r\quad s)(r\quad s) \\ \text{Find the numbers that multiply to }−9\text{ and add to }−8. \end{array}$

Mambo ya$−9$	Jumla ya mambo
\ (-9-9\)” data-valign="top">$1,\space −9$	$−1+9=8$
\ (-9-9\)” data-valign="top">$−1,\space 9$	$1+(−9)=−8^∗$
\ (-9-9\)” data-valign="top">$3,\space −3$	$3+(−3)=0$

$\begin{array} {ll} \text{Use }1,\space -9\text{ as coefficients of the last terms.} &(r+s)(r−9s) \\ \text{Check:} & \\ \hspace{30mm} (r−9s)(r+s) & \\ \hspace{25mm} r^2+rs−9rs−9s^2 & \\ \hspace{30mm} r^2−8rs−9s^2\checkmark & \end{array} $

Mfano$\PageIndex{11}$

Sababu:$a^2−11ab+10b^2$.

Jibu: $(a−b)(a−10b)$

Mfano$\PageIndex{12}$

Sababu:$m^2−13mn+12n^2$.

Jibu: $(m−n)(m−12n)$

Baadhi ya trinomials ni mkuu. Njia pekee ya kuwa na uhakika wa trinomial ni mkuu ni kuorodhesha uwezekano wote na kuonyesha kwamba hakuna hata mmoja wao anayefanya kazi.

Mfano$\PageIndex{13}$

Sababu:$u^2−9uv−12v^2$.

Jibu

Tunahitaji$u$ katika muda wa kwanza wa kila binomial na$v$ katika muda wa pili. Muda wa mwisho wa trinomial ni hasi, hivyo sababu lazima ziwe na ishara tofauti.
$\begin{array} {ll} &u^2−9uv−12v^2 \\ \text{Note that the first terms are }u,\text{ last terms contain }v. &(u\quad v)(u\quad v) \\ \text{Find the numbers that multiply to }−12\text{ and add to }−9. & \end{array} $

Mambo ya$−12$	Jumla ya mambo
\ (-12\)” data-valign="top">$1,−12$ $−1,12$ $2,−6$ $−2,6$ $3,−4$ $−3,4$	$1+(−12)=−11$ $−1+12=11$ $2+(−6)=−4$ $−2+6=4$ $3+(−4)=−1$ $−3+4=1$

Kumbuka hakuna jozi sababu kwamba kutupa$−9$ kama jumla. The trinomial ni mkuu.

Mfano$\PageIndex{14}$

Sababu:$x^2−7xy−10y^2$.

Jibu: mkuu

Mfano$\PageIndex{15}$

Sababu:$p^2+15pq+20q^2$.

Jibu: mkuu

Hebu tufupishe njia tuliyoendeleza tu ili kuzingatia trinomials ya fomu$x^2+bx+c$.

MKAKATI WA KUFAFANUA TRINOMIALS YA FOMU$x^2+bx+c$

Tunapofanya trinomial, tunaangalia ishara za maneno yake kwanza kuamua ishara za mambo ya binomial.

	$ x^{2}+b x+c $
	$ (x+m)(x+n) $
Wakati$ c $ ni chanya,$ m $ na$ n $ uwe na ishara sawa.
$ b $chanya		$ b $hasi
$ m,n $chanya		$ m,n $hasi
$ x^{2}+5 x+6 $		$ x^{2}-6 x+8 $
$ (x+2)(x+3) $		$ (x-4)(x-2) $
ishara sawa		ishara sawa
Wakati$ c $ ni hasi,$ m $ na$ n $ uwe na ishara tofauti.
$ x^{2}+x-12 $		$ x^{2}-2 x-15 $
$ (x+4)(x-3) $		$ (x-5)(x+3) $
ishara za kinyume		ishara za kinyume

Kumbuka kwamba, katika kesi wakati$m$ na$n$ kuwa na ishara tofauti, ishara ya moja yenye thamani kubwa kabisa inafanana na ishara ya$b$.

Factor Trinomials ya fomu shaba ² + bx + c kutumia Jaribio na Hitilafu

Hatua yetu inayofuata ni kuzingatia trinomials ambao mgawo wa kuongoza sio 1, trinomials ya fomu$ax^2+bx+c$.

Kumbuka daima kuangalia kwa GCF kwanza! Wakati mwingine, baada ya kuzingatia GCF, mgawo wa kuongoza wa trinomial unakuwa$1$ na unaweza kuifanya kwa njia ambazo tumetumia hadi sasa. Hebu tufanye mfano ili kuona jinsi hii inavyofanya kazi.

Mfano$\PageIndex{16}$

Sababu kabisa:$4x^3+16x^2−20x$.

Jibu

$\begin{array} {lll} \text{Is there a greatest common factor?} &\qquad &4x^3+16x^2−20x \\ \quad \text{Yes, }GCF=4x.\text{ Factor it.} & &4x(x^2+4x−5) \\ & & \\ & & \\ \text{Binomial, trinomial, or more than three terms?} & & \\ \quad \text{It is a trinomial. So “undo FOIL.”} & &4x(x\quad)(x\quad) \\ & & \\ & & \\ \text{Use a table like the one shown to find two numbers that} & &4x(x−1)(x+5) \\ \text{multiply to }−5\text{ and add to }4. & & \\ & & \\ & & \end{array} $

Mambo ya$−5$	Jumla ya mambo
\ (-5\)” data-valign="top">$−1,5$ $1,−5$	$−1+5=4^∗$ $1+(−5)=−4$

$\begin{array} {l} \text{Check:}\\ \hspace{27mm}4x(x−1)(x+5) \\ \hspace{25mm} 4x(x^2+5x−x−5) \\ \hspace{30mm} 4x(x^2+4x−5) \\ \hspace{25mm} 4x^3+16x2−20x\checkmark \end{array} $

Mfano$\PageIndex{17}$

Sababu kabisa:$5x^3+15x^2−20x$.

Jibu: $5x(x−1)(x+4)$

Mfano$\PageIndex{18}$

Sababu kabisa:$6y^3+18y^2−60y$.

Jibu: $6y(y−2)(y+5)$

Ni nini kinachotokea wakati mgawo wa kuongoza sio$1$ na hakuna GCF? Kuna mbinu kadhaa ambazo zinaweza kutumiwa kuzingatia hizi trinomials. Kwanza tutatumia njia ya Jaribio na Hitilafu.

Hebu tuchunguze trinomial$3x^2+5x+2$.

Kutoka kwa kazi yetu ya awali, tunatarajia hii itafanyika katika binomials mbili.

\[3x^2+5x+2\nonumber\]\[(\quad)(\quad)\nonumber\]

Tunajua maneno ya kwanza ya mambo ya binomial yatazidisha kutupa$3x^2$. Sababu tu ya$3x^2$ ni$1x,\space 3x$. Tunaweza kuwaweka katika binomials.

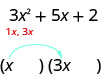
$Polynomial ni 3x mraba pamoja na 5x pamoja na 2. Kuna jozi mbili za mabano, na maneno ya kwanza ndani yao kuwa x na 3x.$

Angalia: Je$1x·3x=3x^2$?

Tunajua masharti ya mwisho ya binomials itazidisha kwa$2$. Kwa kuwa hii trinomial ina maneno yote mazuri, tunahitaji tu kuzingatia mambo mazuri. Sababu pekee za$2$ ni$1$ na$2$. Lakini sasa tuna kesi mbili za kuzingatia kama itafanya tofauti ikiwa tunaandika$1$,$2$ au$2$,$1$.

Ni mambo gani sahihi? Kuamua kwamba, tunazidisha maneno ya ndani na nje.

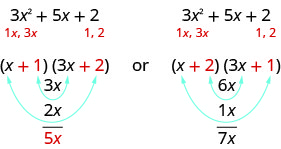
$Kielelezo kinaonyesha 3x mraba wa polynomial pamoja na 5x pamoja na 2 na jozi mbili zinazowezekana za sababu. Moja ni wazi mabano x plus 1 karibu mabano wazi 3x pamoja 2 karibu mabano. Nyingine ni wazi mabano x plus 2 karibu mabano wazi 3x pamoja 1 karibu mabano. Katika kila kesi, mishale inavyoonyeshwa kuunganisha muda wa kwanza wa sababu ya kwanza na muda wa mwisho wa sababu ya pili na muda wa kwanza wa sababu ya pili na muda wa mwisho wa sababu ya kwanza.$

Tangu muda wa kati wa trinomial ni$5x$, sababu katika kesi ya kwanza itafanya kazi. Hebu tumia FOIL ili uangalie.

\[(x+1)(3x+2)\nonumber\]\[3x^2+2x+3x+2\nonumber\]\[3x^2+5x+2\checkmark\nonumber\]

Matokeo yetu ya factoring ni:

\[3x^2+5x+2\nonumber\]\[(x+1)(3x+2)\nonumber\]

Mfano$\PageIndex{19}$: How to Factor a Trinomial Using Trial and Error

Sababu kabisa kutumia jaribio na hitilafu:$3y^2+22y+7$.

Jibu: $Hatua ya 1 ni kuandika trinomial katika utaratibu wa kushuka. Ya trinomial 3 y squared pamoja na 22y pamoja na 7 tayari iko katika utaratibu wa kushuka.$ $Hatua ya 2 ni sababu GCF. Hapa, hakuna.$ $Hatua ya 3 ni Kupata jozi zote sababu ya muda wa kwanza. Sababu pekee hapa ni 1y na 3y. Kwa kuwa kuna jozi moja tu, tunaweza kuweka kila mmoja kama muda wa kwanza katika mabano.$ $Hatua ya 4 ni kupata jozi zote za muda wa tatu. Hapa, jozi pekee ni 1 na 7.$ $Hatua ya 5 ni kupima mchanganyiko wote unaowezekana wa mambo mpaka bidhaa sahihi inapatikana. Kwa sababu zinazowezekana kufungua mabano y pamoja na 1 mabano ya karibu ya wazi mabano 37 pamoja na 7 mabano ya karibu, bidhaa ni 3 y squared pamoja na 10y pamoja na 7. Kwa sababu zinazowezekana kufungua mabano y plus 7 karibu mabano wazi 3y pamoja 1 karibu mabano, bidhaa ni 3 y squared pamoja 22y pamoja na 7, ambayo ni bidhaa sahihi. Kwa hiyo, mambo sahihi ni mabano ya wazi y pamoja na mabano 7 ya karibu ya kufungua mabano 3y pamoja na 1 mabano ya karibu.$ $Hatua ya 6 ni kuangalia kwa kuzidisha.$

Mfano$\PageIndex{20}$

Sababu kabisa kutumia jaribio na hitilafu:$2a^2+5a+3$.

Jibu: $(a+1)(2a+3)$

Mfano$\PageIndex{21}$

Sababu kabisa kutumia jaribio na hitilafu:$4b^2+5b+1$.

Jibu: $(b+1)(4b+1)$

VIPENGELE VYA TRINOMIALS YA FOMU$ax^2+bx+c$ USING TRIAL AND ERROR.

Andika trinomial katika utaratibu wa kushuka kwa digrii kama inahitajika.
Sababu yoyote GCF.
Pata jozi zote za muda wa kwanza.
Pata jozi zote za muda wa tatu.
Jaribu mchanganyiko wote unaowezekana wa mambo mpaka bidhaa sahihi inapatikana.
Angalia kwa kuzidisha.

Kumbuka, wakati muda wa kati ni hasi na muda wa mwisho ni chanya, ishara katika binomials lazima zote ziwe hasi.

Mfano$\PageIndex{22}$

Sababu kabisa kutumia jaribio na hitilafu:$6b^2−13b+5$.

Jibu

The trinomial tayari iko katika utaratibu wa kushuka.	$.$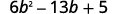
Pata sababu za muda wa kwanza.	$.$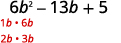
Pata sababu za muda wa mwisho. Fikiria ishara. Tangu muda wa mwisho,$5$, ni chanya mambo yake lazima wote kuwa chanya au wote kuwa hasi. Mgawo wa muda wa kati ni hasi, kwa hiyo tunatumia sababu hasi.	$.$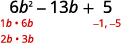

Fikiria mchanganyiko wote wa mambo.

$6b^2−13b+5$
Sababu zinazowezekana	Bidhaa
\ (6b ^ 2,113b+5\) Sababu zinazowezekana” data-valign="top">$(b−1)(6b−5)$	\ (6b ^ 2,113b+5\) Bidhaa” data-valign="top">$6b^2−11b+5$
\ (6b ^ 2,113b+5\) Sababu zinazowezekana” data-valign="top">$(b−5)(6b−1)$	\ (6b ^ 2,113b+5\) Bidhaa” data-valign="top">$6b^2−31b+5$
\ (6b ^ 2,113b+5\) Sababu zinazowezekana” data-valign="top">$(2b−1)(3b−5)$	\ (6b ^ 2,113b+5\) Bidhaa” data-valign="middle">$6b^2−13b+5^∗$
\ (6b ^ 2,113b+5\) Sababu zinazowezekana” data-valign="top">$(2b−5)(3b−1)$	\ (6b ^ 2,113b+5\) Bidhaa” data-valign="middle">$6b^2−17b+5$

$\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial.} &(2b−1)(3b−5) \\ \text{Check by multiplying:} & \\ \hspace{50mm} (2b−1)(3b−5) & \\ \hspace{47mm} 6b^2−10b−3b+5 & \\ \hspace{50mm} 6b^2−13b+5\checkmark & \end{array} $

Mfano$\PageIndex{23}$

Sababu kabisa kutumia jaribio na hitilafu:$8x^2−14x+3$.

Jibu: $(2x−3)(4x−1)$

Mfano$\PageIndex{24}$

Sababu kabisa kutumia jaribio na hitilafu:$10y^2−37y+7$.

Jibu: $(2y−7)(5y−1)$

Wakati sisi sababu kujieleza, sisi daima kuangalia kwa sababu kubwa ya kawaida kwanza. Ikiwa maneno hayana sababu kubwa ya kawaida, hawezi kuwa na moja katika mambo yake ama. Hii inaweza kutusaidia kuondoa baadhi ya mchanganyiko wa sababu zinazowezekana.

Mfano$\PageIndex{25}$

Sababu kabisa kutumia jaribio na hitilafu:$18x^2−37xy+15y^2$.

Jibu

The trinomial tayari iko katika utaratibu wa kushuka.	$.$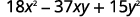
Pata sababu za muda wa kwanza.	$.$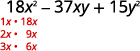
Pata sababu za muda wa mwisho. Fikiria ishara. Kwa kuwa 15 ni chanya na mgawo wa muda wa kati ni hasi, tunatumia sababu hasi.	$.$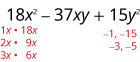

Fikiria mchanganyiko wote wa mambo.

$Jedwali hili linaonyesha sababu zinazowezekana na bidhaa zinazofanana za trinomial 18 x squared minus 37xy pamoja na 15 y squared. Katika baadhi ya jozi ya mambo, wakati sababu moja ina maneno mawili na sababu ya kawaida, jambo hilo linaonyeshwa. Katika hali hiyo, bidhaa sio chaguo kwa sababu ikiwa trinomial haina mambo ya kawaida, basi hakuna sababu inaweza kuwa na sababu ya kawaida. Sababu: wazi mabano x minus 1y karibu mabano wazi mabano 18x minus 15y karibu mabano, yalionyesha. Sababu, mabano ya wazi x minus 15y karibu mabano wazi mabano 18x minus 1y karibu mabano; bidhaa: 18 x squared minus 271xy pamoja 15 y squared. Factor wazi mabano x minus 3y karibu mabano wazi mabano 18x minus 5 y karibu mabano; bidhaa: 18 x squared minus 59xy pamoja 15 y squared. Sababu: wazi mabano x minus 5y karibu mabano wazi mabano 18x minus 3y karibu mabano yalionyesha. Sababu: wazi mabano 2x minus 1y karibu mabano wazi mabano 9x minus 15y karibu mabano yalionyesha. Sababu: wazi mabano 2x minus 15y karibu mabano wazi mabano 9x minus 1y karibu mabano; bidhaa 18 x squared minus 137 xy pamoja 15y mraba. Sababu: wazi mabano 2x minus 3y karibu mabano wazi mabano 9x bala 5y karibu mabano; bidhaa: 18 x squared minus 37xy pamoja 15 y squared, ambayo ni ya awali trinomial. Sababu: wazi mabano 2x minus 57 karibu mabano wazi mabano 9x minus 3y karibu mabano yalionyesha. Sababu: wazi mabano 3x minus 1y karibu mabano wazi mabano 6x minus 15y karibu mabano yalionyesha. Sababu: wazi mabano 3x minus 15y karibu mabano yalionyesha wazi mabano 6x minus 1y karibu mabano. Sababu: wazi mabano 3x minus 3y karibu mabano yalionyesha wazi mabano 6x minus 5y.$

$\begin{array} {ll} \text{The correct factors are those whose product is} & \\ \text{the original trinomial.} &(2x−3y)(9x−5y) \\ \text{Check by multiplying:} & \\ & \\ & \\ & \\ \hspace{50mm} (2x−3y)(9x−5y) & \\ \hspace{45mm}18x^2−10xy−27xy+15y^2 & \\ \hspace{47mm}18x^2−37xy+15y^2\checkmark & \end{array} $

Mfano$\PageIndex{26}$

Sababu kabisa kutumia jaribio na hitilafu$18x^2−3xy−10y^2$.

Jibu: $(3x+2y)(6x−5y)$

Mfano$\PageIndex{27}$

Sababu kabisa kutumia jaribio na hitilafu:$30x^2−53xy−21y^2$.

Jibu: $(3x+y)(10x−21y)$

Usisahau kuangalia GCF kwanza na kumbuka kama mgawo wa kuongoza ni hasi, hivyo ni GCF.

Mfano$\PageIndex{28}$

Sababu kabisa kutumia jaribio na hitilafu:$−10y^4−55y^3−60y^2$.

Jibu

	$.$
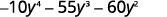
Angalia sababu kubwa ya kawaida, hivyo fikiria kwanza.	$.$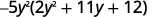
Sababu ya trinomial.	$.$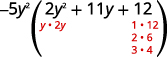

Fikiria mchanganyiko wote.

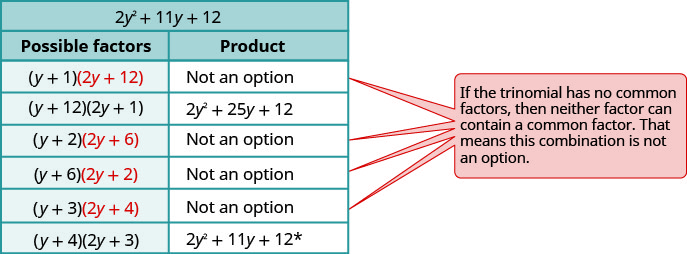
$Jedwali hili linaonyesha sababu zinazowezekana na bidhaa za trinomial 2 y squared pamoja na 11y pamoja na 12. Katika baadhi ya jozi ya mambo, wakati sababu moja ina maneno mawili na sababu ya kawaida, jambo hilo linaonyeshwa. Katika hali hiyo, bidhaa sio chaguo kwa sababu ikiwa trinomial haina mambo ya kawaida, basi hakuna sababu inaweza kuwa na sababu ya kawaida. sababu: y pamoja 1, 2y pamoja na 12 yalionyesha. Sababu: y pamoja na 12, 2y pamoja na 1; bidhaa: 2 y squared pamoja 25y pamoja na 12. sababu: y pamoja na 2, 2y pamoja na 6 yalionyesha. sababu: y pamoja na 6, 2y pamoja na 2 yalionyesha. sababu: y pamoja 3, 2y pamoja na 4 yalionyesha. Sababu: y pamoja na 4, 2y pamoja na 3; bidhaa: 2 y squared pamoja na 11y pamoja na 12. Hii ni trinomial ya awali.$

$\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial. Remember to include} & \\ \text{the factor }−5^y2. &−5y^2(y+4)(2y+3) \\ \text{Check by multiplying:} & \\ \hspace{50mm} −5y^2(y+4)(2y+3) & \\ \hspace{45mm} −5y^2(2y^2+8y+3y+12) & \\ \hspace{47mm}−10y^4−55y^3−60y^2\checkmark & \end{array} $

Mfano$\PageIndex{29}$

Sababu kabisa kutumia jaribio na hitilafu:$15n^3−85n^2+100n$.

Jibu: $5n(n−4)(3n−5)$

Mfano$\PageIndex{30}$

Sababu kabisa kutumia jaribio na hitilafu:$56q^3+320q^2−96q$.

Jibu: $8q(q+6)(7q−2)$

Factor Trinomials ya Fomu$ax^2+bx+c$ kwa kutumia “$ac$” Njia

Njia nyingine ya kuzingatia trinomials ya fomu$ax^2+bx+c$ ni njia “$ac$”. (Njia “$ac$” wakati mwingine huitwa njia ya makundi.) Njia “$ac$” ni kweli ugani wa mbinu ulizotumia katika sehemu ya mwisho ili kuzingatia trinomials na mgawo wa kuongoza moja. Njia hii imeundwa sana (hiyo ni hatua kwa hatua), na inafanya kazi daima!

Mfano$\PageIndex{31}$: How to Factor Trinomials using the “ac” Method

Sababu kwa kutumia “$ac$” njia:$6x^2+7x+2$.

Jibu: $Hatua ya 1 ni sababu GCF. Hakuna katika 6 x squared pamoja 7x pamoja 2.$ $Hatua ya 2 ni kupata bidhaa ya a na c. bidhaa ya 6 na 2 ni 12.$ $Hatua ya 3 ni kupata namba 2 m na n vile kwamba mn ni ac na m plus n ni b Hivyo tunahitaji idadi kwamba kuzidisha kwa 12 na kuongeza 7. Sababu zote mbili lazima ziwe chanya. Mara 3 4 ni 12 na 3 pamoja na 4 ni 7.$ $Hatua ya 4 ni kupasuliwa muda wa kati kwa kutumia m na n Hivyo sisi kuandika upya 7 x kama 3x pamoja 4x. Itakuwa kutoa matokeo sawa kama sisi kutumika 4x pamoja 3x. Kuandika upya, tunapata 6 x mraba pamoja na 3x pamoja na 4x pamoja na 2. Angalia kwamba hii ni sawa na polynomial ya awali. Sisi tu mgawanyiko wa muda wa kati ili kupata fomu muhimu zaidi$ $Hatua ya 5 ni kuzingatia kwa kikundi. Hivyo, sisi kupata, 3x wazi mabano 2x pamoja 1 karibu mabano pamoja 2 wazi mabano 2x pamoja 1 karibu mabano. Hii ni sawa na 2x plus 1, 3x plus 2.$ $Hatua ya 6 ni kuangalia kwa kuzidisha mambo.$

Mfano$\PageIndex{32}$

Sababu kwa kutumia “$ac$” njia:$6x^2+13x+2$.

Jibu: $(x+2)(6x+1)$

Mfano$\PageIndex{33}$

Sababu kwa kutumia “$ac$” njia:$4y^2+8y+3$.

Jibu: $(2y+1)(2y+3)$

Njia “$ac$” inafupishwa hapa.

VIPENGELE VYA TRINOMIALS YA FOMU$ax^2+bx+c$ USING THE “$ac$” METHOD.

Sababu yoyote GCF.
Pata bidhaa$ac$.
Pata namba mbili$m$ na$n$ kwamba:
$\begin{array} {ll} \text{Multiply to }ac &m·n=a·c \\ \text{Add to }b &m+n=b \\ &ax^2+bx+c \end{array} $
Split muda wa kati kwa kutumia$m$ na$n$. $ax^2+mx+nx+c$
Sababu kwa kikundi.
Angalia kwa kuzidisha mambo.

Usisahau kuangalia kwa sababu ya kawaida!

Mfano$\PageIndex{34}$

Sababu kwa kutumia njia ya '“$ac$”:$10y^2−55y+70$.

Jibu

Je, kuna sababu kubwa ya kawaida?
Ndiyo. GCF ni$5$.		$.$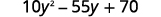
Factor yake.		$.$
Ya trinomial ndani ya mabano ina mgawo wa kuongoza ambao sio$1$.		$.$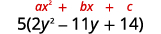
Pata bidhaa$ac$.	$ac=28$
Pata namba mbili zinazozidisha$ac$	$(−4)(−7)=28$
na uongeze kwenye$b$.	$−4(−7)=−11$
Split muda wa kati.		$.$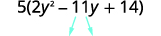
		$.$
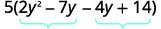
Fanya trinomial kwa kikundi.		$.$
		$.$
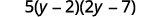
Angalia kwa kuzidisha mambo yote matatu. $\hspace{50mm} 5(y−2)(2y−7)$ $\hspace{45mm} 5(2y^2−7y−4y+14)$ $\hspace{48mm} 5(2y^2−11y+14)$ $\hspace{49mm} 10y^2−55y+70\checkmark$

Mfano$\PageIndex{35}$

Sababu kwa kutumia “$ac$” njia:$16x^2−32x+12$.

Jibu: $4(2x−3)(2x−1)$

Mfano$\PageIndex{36}$

Sababu kwa kutumia “$ac$” njia:$18w^2−39w+18$.

Jibu: $3(3w−2)(2w−3)$

Sababu Kutumia Kubadilisha

Wakati mwingine trinomial haionekani kuwa katika$ax^2+bx+c$ fomu. Hata hivyo, tunaweza mara nyingi kufanya badala ya kufikiri ambayo itatuwezesha kuifanya$ax^2+bx+c$ fomu hiyo. Hii inaitwa factoring na badala. Ni kiwango cha kutumia$u$ kwa ajili ya kubadilisha.

Katika$ax^2+bx+c$, muda wa kati ina variable,$x$, na mraba wake,$x^2$, ni sehemu ya kutofautiana ya muda wa kwanza. Angalia uhusiano huu unapojaribu kupata nafasi.

Mfano$\PageIndex{37}$

Sababu kwa badala:$x^4−4x^2−5$.

Jibu

Sehemu ya kutofautiana ya muda wa kati ni$x^2$ na mraba wake,$x^4$, ni sehemu ya kutofautiana ya muda wa kwanza. (Tunajua$(x^2)^2=x^4)$. Ikiwa tunaruhusu$u=x^2$, tunaweza kuweka trinomial yetu kwa$ax^2+bx+c$ fomu tunayohitaji kuifanya.

	$x^4−4x^2−5$
Andika upya trinomial kujiandaa kwa ajili ya ubadilishaji.	$(x^2)^2−4(x^2)-5$
Hebu$u=x^2$ na mbadala.	$(u)^2−4(u)-5$
Sababu ya trinomial.	$(u+1)(u-5)$
Badilisha nafasi$u$ na$x^2$.	$(x^2+1)(x^2-5)$
Angalia: $\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}$

Mfano$\PageIndex{38}$

Sababu kwa badala:$h^4+4h^2−12$.

Jibu: $(h^2−2)(h^2+6)$

Mfano$\PageIndex{39}$

Sababu kwa badala:$y^4−y^2−20$.

Jibu: $(y^2+4)(y^2−5)$

Wakati mwingine maneno ya kubadilishwa sio monomial.

Mfano$\PageIndex{40}$

Sababu kwa badala:$(x−2)^2+7(x−2)+12$

Jibu

Binomial katika muda wa kati,$(x−2)$ ni mraba katika muda wa kwanza. Kama sisi basi$u=x−2$ na mbadala, trinomial yetu itakuwa katika$ax^2+bx+c$ fomu.

	$.$
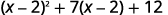
Andika upya trinomial kujiandaa kwa ajili ya ubadilishaji.	$.$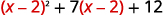
Hebu$u=x−2$ na mbadala.	$.$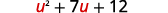
Sababu ya trinomial.	$.$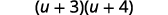
Badilisha nafasi$u$ na$x−2$.	$.$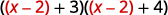
Kurahisisha ndani ya mabano.	$.$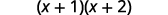

Hii inaweza pia kuwa factored na kwanza kuzidisha nje$(x−2)^2$$7(x−2)$ na kisha kuchanganya kama maneno na kisha factoring. Wanafunzi wengi wanapendelea njia ya kubadilisha.

Mfano$\PageIndex{41}$

Sababu kwa badala:$(x−5)^2+6(x−5)+8$.

Jibu: $(x−3)(x−1)$

Mfano$\PageIndex{42}$

Sababu kwa badala:$(y−4)^2+8(y−4)+15$.

Jibu: $(y−1)(y+1)$

Tazama video hii kwa maelekezo ya ziada na mazoezi na kuzingatia.

Dhana muhimu

Jinsi ya kuzingatia trinomials ya fomu$x^2+bx+c$.
1. Andika mambo kama binomials mbili na maneno ya kwanza x. $\quad \begin{array} (l) x^2+bx+c \\ (x\quad)(x\quad)\end{array}$
2. Kupata namba mbili$m$ na$n$ kwamba
  $\begin{array} {ll} \text{multiply to} &c,\space m·n=c \\ \text{add to} &b,\space m+n=b\end{array}$
3. Tumia$m$ na$n$ kama masharti ya mwisho ya mambo. $\qquad (x+m)(x+n)$
4. Angalia kwa kuzidisha mambo.
Mkakati wa Kuzingatia Trinomials ya Fomu$x^2+bx+c$: Tunapofanya trinomial, tunaangalia ishara za masharti yake kwanza kuamua ishara za mambo ya binomial.

Kwa trinomials ya fomu:$x^2+bx+c = (x+m)(x+n)$

Wakati$c$ ni chanya,$m$ na$n$ lazima uwe na ishara sawa (na hii itakuwa ishara ya$b$ ).

Mifano:$x^2+5x+6=(x+2)(x+3)$,$x^2−6x+8 = (x−4)(x−2)$

Wakati$c$ ni hasi,$m$ na$n$ kuwa na ishara kinyume. kubwa ya$m$ na$n$ itakuwa na ishara ya$b$.

Mifano:$x^2+x−12=(x+4)(x−3)$,$x^2−2x−15=(x−5)(x+3)$

Angalia kwamba, katika kesi wakati$m$ na$n$ kuwa na ishara tofauti, ishara ya moja yenye thamani kubwa kabisa inafanana na ishara ya$b$.
Jinsi ya kuzingatia trinomials ya fomu kwa$ax^2+bx+c$ kutumia jaribio na hitilafu.
1. Andika trinomial katika utaratibu wa kushuka kwa digrii kama inahitajika.
2. Sababu yoyote GCF.
3. Pata jozi zote za muda wa kwanza.
4. Pata jozi zote za muda wa tatu.
5. Jaribu mchanganyiko wote unaowezekana wa mambo mpaka bidhaa sahihi inapatikana.
6. Angalia kwa kuzidisha.
Jinsi ya kuzingatia trinomials ya fomu$ax^2+bx+c$ kwa kutumia njia “$ac$”.
1. Sababu yoyote GCF.
2. Pata bidhaa$ac$.
3. Pata namba mbili$m$ na$n$ kwamba:
  $\begin{array} {ll} \text{Multiply to }ac. &m·n=a·c \\ \text{Add to }b. &m+n=b \\ &ax^2+bx+c\end{array}$
4. Split muda wa kati kwa kutumia$m$ na$n$. $\quad ax^2+mx+nx+c$
5. Sababu kwa kikundi.
6. Angalia kwa kuzidisha mambo.

	\((x+m)(x+n)\)
Foil kupata bidhaa.	\(x^{2}+m x+n x+m n\)
Factor GCF kutoka suala la kati.	\(x^{2}+(m+n) x+m n\)
Trinomial yetu ni ya fomu\(x^2+bx+c\).	\(\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}\)

Mambo ya\(−9\)	Jumla ya mambo
\ (-9-9\)” data-valign="top">\(1,\space −9\)	\(−1+9=8\)
\ (-9-9\)” data-valign="top">\(−1,\space 9\)	\(1+(−9)=−8^∗\)
\ (-9-9\)” data-valign="top">\(3,\space −3\)	\(3+(−3)=0\)

	\( x^{2}+b x+c \)
	\( (x+m)(x+n) \)
Wakati\( c \) ni chanya,\( m \) na\( n \) uwe na ishara sawa.
\( b \)chanya		\( b \)hasi
\( m,n \)chanya		\( m,n \)hasi
\( x^{2}+5 x+6 \)		\( x^{2}-6 x+8 \)
\( (x+2)(x+3) \)		\( (x-4)(x-2) \)
ishara sawa		ishara sawa
Wakati\( c \) ni hasi,\( m \) na\( n \) uwe na ishara tofauti.
\( x^{2}+x-12 \)		\( x^{2}-2 x-15 \)
\( (x+4)(x-3) \)		\( (x-5)(x+3) \)
ishara za kinyume		ishara za kinyume

\(6b^2−13b+5\)
Sababu zinazowezekana	Bidhaa
\ (6b ^ 2,113b+5\) Sababu zinazowezekana” data-valign="top">\((b−1)(6b−5)\)	\ (6b ^ 2,113b+5\) Bidhaa” data-valign="top">\(6b^2−11b+5\)
\ (6b ^ 2,113b+5\) Sababu zinazowezekana” data-valign="top">\((b−5)(6b−1)\)	\ (6b ^ 2,113b+5\) Bidhaa” data-valign="top">\(6b^2−31b+5\)
\ (6b ^ 2,113b+5\) Sababu zinazowezekana” data-valign="top">\((2b−1)(3b−5)\)	\ (6b ^ 2,113b+5\) Bidhaa” data-valign="middle">\(6b^2−13b+5^∗\)
\ (6b ^ 2,113b+5\) Sababu zinazowezekana” data-valign="top">\((2b−5)(3b−1)\)	\ (6b ^ 2,113b+5\) Bidhaa” data-valign="middle">\(6b^2−17b+5\)

	\(x^4−4x^2−5\)
Andika upya trinomial kujiandaa kwa ajili ya ubadilishaji.	\((x^2)^2−4(x^2)-5\)
Hebu\(u=x^2\) na mbadala.	\((u)^2−4(u)-5\)
Sababu ya trinomial.	\((u+1)(u-5)\)
Badilisha nafasi\(u\) na\(x^2\).	\((x^2+1)(x^2-5)\)
Angalia: \(\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}\)

Je, kuna sababu kubwa ya kawaida?
Ndiyo. GCF ni\(5\).		$.$
Factor yake.		$.$
Ya trinomial ndani ya mabano ina mgawo wa kuongoza ambao sio\(1\).		$.$
Pata bidhaa\(ac\).	\(ac=28\)
Pata namba mbili zinazozidisha\(ac\)	\((−4)(−7)=28\)
na uongeze kwenye\(b\).	\(−4(−7)=−11\)
Split muda wa kati.		$.$
		$.$
Fanya trinomial kwa kikundi.		$.$
		$.$
Angalia kwa kuzidisha mambo yote matatu. \(\hspace{50mm} 5(y−2)(2y−7)\) \(\hspace{45mm} 5(2y^2−7y−4y+14)\) \(\hspace{48mm} 5(2y^2−11y+14)\) \(\hspace{49mm} 10y^2−55y+70\checkmark\)

	$.$
Andika upya trinomial kujiandaa kwa ajili ya ubadilishaji.	$.$
Hebu\(u=x−2\) na mbadala.	$.$
Sababu ya trinomial.	$.$
Badilisha nafasi\(u\) na\(x−2\).	$.$
Kurahisisha ndani ya mabano.	$.$

Malengo ya kujifunza

Sababu Trinomials ya Fomu\(x^2+bx+c\)

Mfano\(\PageIndex{1}\): How to Factor a Trinomial of the form \(x^2+bx+c\)

Mfano\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\)

Mfano\(\PageIndex{4}\)

Mfano\(\PageIndex{5}\)

Mfano\(\PageIndex{6}\)

Mfano\(\PageIndex{7}\)

Mfano\(\PageIndex{8}\)

Mfano\(\PageIndex{9}\)

Mfano\(\PageIndex{10}\)

Mfano\(\PageIndex{11}\)

Mfano\(\PageIndex{12}\)

Mfano\(\PageIndex{13}\)

Mfano\(\PageIndex{14}\)

Mfano\(\PageIndex{15}\)

MKAKATI WA KUFAFANUA TRINOMIALS YA FOMU\(x^2+bx+c\)

Factor Trinomials ya fomu shaba 2 + bx + c kutumia Jaribio na Hitilafu

Mfano\(\PageIndex{16}\)

Mfano\(\PageIndex{17}\)

Mfano\(\PageIndex{18}\)

Mfano\(\PageIndex{19}\): How to Factor a Trinomial Using Trial and Error

Mfano\(\PageIndex{20}\)

Mfano\(\PageIndex{21}\)

VIPENGELE VYA TRINOMIALS YA FOMU\(ax^2+bx+c\) USING TRIAL AND ERROR.

Mfano\(\PageIndex{22}\)

Mfano\(\PageIndex{23}\)

Mfano\(\PageIndex{24}\)

Mfano\(\PageIndex{25}\)

Mfano\(\PageIndex{26}\)

Mfano\(\PageIndex{27}\)

Mfano\(\PageIndex{28}\)

Mfano\(\PageIndex{29}\)

Mfano\(\PageIndex{30}\)

Factor Trinomials ya Fomu\(ax^2+bx+c\) kwa kutumia “\(ac\)” Njia

Mfano\(\PageIndex{31}\): How to Factor Trinomials using the “ac” Method

Mfano\(\PageIndex{32}\)

Mfano\(\PageIndex{33}\)

VIPENGELE VYA TRINOMIALS YA FOMU\(ax^2+bx+c\) USING THE “\(ac\)” METHOD.

Mfano\(\PageIndex{34}\)

Mfano\(\PageIndex{35}\)

Mfano\(\PageIndex{36}\)

Sababu Kutumia Kubadilisha

Mfano\(\PageIndex{37}\)

Mfano\(\PageIndex{38}\)

Mfano\(\PageIndex{39}\)

Mfano\(\PageIndex{40}\)

Mfano\(\PageIndex{41}\)

Mfano\(\PageIndex{42}\)

Dhana muhimu

Factor Trinomials ya fomu shaba ² + bx + c kutumia Jaribio na Hitilafu