6.2: Sababu kubwa ya kawaida na Factor kwa Kundi
- Page ID
- 176113
Mwishoni mwa sehemu hii, utaweza:
- Pata sababu kubwa ya kawaida ya maneno mawili au zaidi
- Sababu kubwa ya kawaida sababu kutoka polynomial
- Sababu kwa kikundi
Pata sababu kubwa ya kawaida ya maneno mawili au Zaidi
Mapema tuliongeza mambo pamoja ili kupata bidhaa. Sasa, tutabadilisha mchakato huu; tutaanza na bidhaa na kisha kuivunja ndani ya mambo yake. Kugawanyika bidhaa katika mambo inaitwa factoring.
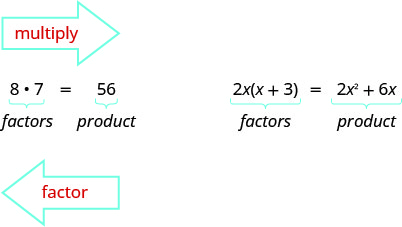
Tumejifunza jinsi ya kuhesabu namba ili kupata angalau ya kawaida (LCM) ya namba mbili au zaidi. Sasa tutazingatia maneno na kupata sababu kubwa ya kawaida ya maneno mawili au zaidi. Njia tunayotumia ni sawa na kile tulichotumia kupata LCM.
Sababu kubwa zaidi ya kawaida (GCF) ya maneno mawili au zaidi ni usemi mkubwa ambao ni sababu ya maneno yote.
Tunafupisha hatua tunazotumia ili kupata sababu kubwa zaidi ya kawaida.
- Factor kila mgawo katika primes. Andika vigezo vyote na vielelezo katika fomu iliyopanuliwa.
- Orodha ya mambo yote-vinavyolingana mambo ya kawaida katika safu. Katika kila safu, duru mambo ya kawaida.
- Kuleta mambo ya kawaida ambayo maneno yote hushiriki.
- Kuzidisha mambo.
Mfano unaofuata utatuonyesha hatua za kupata sababu kubwa zaidi ya maneno matatu.
Kupata kubwa ya kawaida sababu ya\(21x^3,\space 9x^2,\space 15x\).
- Jibu
-
Factor kila mgawo katika primes na kuandika vigezo na exponents katika fomu kupanua. Circle mambo ya kawaida katika kila safu. Kuleta mambo ya kawaida. 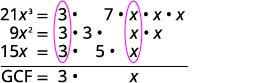
Kuzidisha mambo. GCF\(=3x\) GCF ya\(21x^3\),\(9x^2\) na\(15x\) ni\(3x\).
Pata sababu kubwa zaidi ya kawaida:\(25m^4,\space 35m^3,\space 20m^2.\)
- Jibu
-
\(5m^2\)
Kupata kubwa ya kawaida sababu:\(14x^3,\space 70x^2,\space 105x\).
- Jibu
-
\(7x\)
Sababu ya Sababu kuu ya kawaida kutoka kwa Polynomial
Wakati mwingine ni muhimu kuwakilisha idadi kama bidhaa ya mambo, kwa mfano, 12 kama\(2·6\) au\(3·4\). Katika algebra, inaweza pia kuwa na manufaa kuwakilisha polynomial katika fomu iliyopangwa. Tutaanza na bidhaa, kama vile\(3x^2+15x\), na kuishia na mambo yake,\(3x(x+5)\). Ili kufanya hivyo tunatumia Mali ya Usambazaji “kwa reverse.”
Tunasema Mali ya Distributive hapa kama ulivyoiona katika sura za awali na “kinyume chake.”
Ikiwa a, b, na c ni namba halisi, basi
\[a(b+c)=ab+ac \quad \text{and} \quad ab+ac=a(b+c)\nonumber\]
Fomu upande wa kushoto hutumiwa kuzidi. Fomu ya haki hutumiwa kuzingatia.
Kwa hiyo unatumiaje Mali ya Distributive kwa sababu ya polynomial? Wewe tu kupata GCF ya maneno yote na kuandika polynomial kama bidhaa!
Sababu:\(8m^3−12m^2n+20mn^2\).
- Jibu
-




Sababu:\(9xy^2+6x^2y^2+21y^3\).
- Jibu
-
\(3y^2(3x+2x^2+7y)\)
Sababu:\(3p^3−6p^2q+9pq^3\).
- Jibu
-
\(3p(p^2−2pq+3q^3)\)
- Pata GCF ya masharti yote ya polynomial.
- Andika upya kila neno kama bidhaa kwa kutumia GCF.
- Tumia “reverse” Mali ya Distributive kwa sababu ya kujieleza.
- Angalia kwa kuzidisha mambo.
Tunatumia “factor” kama nomino na kitenzi:
\[\begin{array} {ll} \text{Noun:} &\hspace{50mm} 7 \text{ is a factor of }14 \\ \text{Verb:} &\hspace{50mm} \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
Sababu:\(5x^3−25x^2\).
- Jibu
-
Kupata GCF ya\(5x^3\) na\(25x^2\). 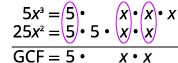
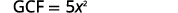
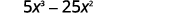
Andika upya kila neno. 
Sababu ya GCF. 
Angalia:
\[5x^2(x−5) \nonumber\]\[5x^2·x−5x^2·5 \nonumber\]
\[5x^3−25x^2 \checkmark\nonumber\]
Sababu:\(2x^3+12x^2\).
- Jibu
-
\(2x^2(x+6)\)
Sababu:\(6y^3−15y^2\).
- Jibu
-
\(3y^2(2y−5)\)
Sababu:\(8x^3y−10x^2y^2+12xy^3\).
- Jibu
-
GCF ya\(8x^3y,\space −10x^2y^2,\) na\(12xy^3\)
ni\(2xy\).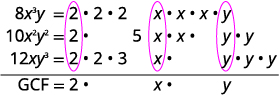

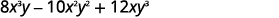
Andika upya kila neno kwa kutumia GCF,\(2xy\). 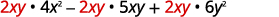
Sababu ya GCF. 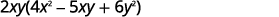
Angalia:
\[2xy(4x^2−5xy+6y^2)\nonumber\]\[2xy·4x^2−2xy·5xy+2xy·6y^2\nonumber\]
\[8x^3y−10x^2y^2+12xy^3\checkmark\nonumber\]
Sababu:\(15x^3y−3x^2y^2+6xy^3\).
- Jibu
-
\(3xy(5x^2−xy+2y^2)\)
Sababu:\(8a^3b+2a^2b^2−6ab^3\).
- Jibu
-
\(2ab(4a^2+ab−3b^2)\)
Wakati mgawo wa kuongoza ni hasi, tunaona hasi nje kama sehemu ya GCF.
Sababu:\(−4a^3+36a^2−8a\).
- Jibu
-
Mgawo wa kuongoza ni hasi, hivyo GCF itakuwa hasi.
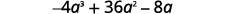
Andika upya kila neno kwa kutumia GCF,\(−4a\). 
Sababu ya GCF. 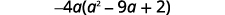
Angalia:
\[−4a(a^2−9a+2)\nonumber\]\[−4a·a^2−(−4a)·9a+(−4a)·2\nonumber\]
\[−4a^3+36a^2−8a\checkmark\nonumber\]
Sababu:\(−4b^3+16b^2−8b\).
- Jibu
-
\(−4b(b^2−4b+2)\)
Sababu:\(−7a^3+21a^2−14a\).
- Jibu
-
\(−7a(a^2−3a+2)\)
Hadi sasa mambo yetu makubwa ya kawaida yamekuwa monomials. Katika mfano unaofuata, sababu kubwa zaidi ni binomial.
Sababu:\(3y(y+7)−4(y+7)\).
- Jibu
-
GCF ni binomial\(y+7\).
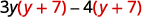
Sababu ya GCF,\((y+7)\). \((y+7)(3 y-4)\) Angalia mwenyewe kwa kuzidisha.
Sababu:\(4m(m+3)−7(m+3)\).
- Jibu
-
\((m+3)(4m−7)\)
Sababu:\(8n(n−4)+5(n−4)\).
- Jibu
-
\((n−4)(8n+5)\)
Kipengele kwa Kundi
Wakati mwingine hakuna sababu ya kawaida ya masharti yote ya polynomial. Wakati kuna maneno manne tunatenganisha polynomial katika sehemu mbili na maneno mawili katika kila sehemu. Kisha angalia GCF katika kila sehemu. Ikiwa polynomial inaweza kuzingatiwa, utapata sababu ya kawaida inatoka kutoka sehemu zote mbili. Sio polynomials zote zinaweza kuzingatiwa. Kama idadi fulani ni mkuu, baadhi ya polynomials ni mkuu.
Sababu kwa kikundi:\(xy+3y+2x+6\).
- Jibu
-




Sababu kwa kikundi:\(xy+8y+3x+24\).
- Jibu
-
\((x+8)(y+3)\)
Sababu kwa kikundi:\(ab+7b+8a+56\).
- Jibu
-
\((a+7)(b+8)\)
- Masharti ya kikundi na mambo ya kawaida.
- Factor nje sababu ya kawaida katika kila kikundi.
- Fanya sababu ya kawaida kutoka kwa maneno.
- Angalia kwa kuzidisha mambo.
Sababu kwa kikundi: ⓐ\(x^2+3x−2x−6\) ⓑ\(6x^2−3x−4x+2\).
- Jibu
-
ⓐ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &x^2+3x−2x−6 \\ \text{Separate into two parts.} &x^2+3x\quad −2x−6 \\ \begin{array} {l} \text{Factor the GCF from both parts. Be careful} \\ \text{with the signs when factoring the GCF from} \\ \text{the last two terms.} \end{array} &x(x+3)−2(x+3) \\ \text{Factor out the common factor.} &(x+3)(x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
ⓑ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &6x^2−3x−4x+2 \\ \text{Separate into two parts.} &6x^2−3x\quad −4x+2\\ \text{Factor the GCF from both parts.} &3x(2x−1)−2(2x−1) \\ \text{Factor out the common factor.} &(2x−1)(3x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
Sababu kwa kikundi: ⓐ\(x^2+2x−5x−10\) ⓑ\(20x^2−16x−15x+12\).
- Jibu
-
ⓐ\((x−5)(x+2)\)
ⓑ\((5x−4)(4x−3)\)
Sababu kwa kikundi: ⓐ\(y^2+4y−7y−28\) ⓑ\(42m^2−18m−35m+15\).
- Jibu
-
ⓐ\((y+4)(y−7)\)
ⓑ\((7m−3)(6m−5)\)
Dhana muhimu
- Jinsi ya kupata sababu kubwa ya kawaida (GCF) ya maneno mawili.
- Factor kila mgawo katika primes. Andika vigezo vyote na vielelezo katika fomu iliyopanuliwa.
- Orodha ya mambo yote-vinavyolingana mambo ya kawaida katika safu. Katika kila safu, duru mambo ya kawaida.
- Kuleta mambo ya kawaida ambayo maneno yote hushiriki.
- Kuzidisha mambo.
- Distributive Mali: Kama\(a\),\(b\) na\(c\) ni idadi halisi, basi
\[a(b+c)=ab+ac\quad \text{and}\quad ab+ac=a(b+c)\nonumber\]
Fomu upande wa kushoto hutumiwa kuzidi. Fomu ya haki hutumiwa kuzingatia. - Jinsi ya kuzingatia sababu kubwa zaidi kutoka kwa polynomial.
- Pata GCF ya masharti yote ya polynomial.
- Andika upya kila neno kama bidhaa kwa kutumia GCF.
- Tumia “reverse” Mali ya Distributive kwa sababu ya kujieleza.
- Angalia kwa kuzidisha mambo.
- Kipengele kama Nomino na Kitenzi: Tunatumia “factor” kama nomino na kitenzi.
\[\begin{array} {ll} \text{Noun:} &\quad 7 \text{ is a factor of } 14\\ \text{Verb:} &\quad \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
- Jinsi ya kuzingatia kwa kikundi.
- Masharti ya kikundi na mambo ya kawaida.
- Factor nje sababu ya kawaida katika kila kikundi.
- Fanya sababu ya kawaida kutoka kwa maneno.
- Angalia kwa kuzidisha mambo.
faharasa
- kuchanganua
- Kugawanyika bidhaa katika mambo inaitwa factoring.
- sababu kubwa ya kawaida
- Sababu kubwa zaidi ya kawaida (GCF) ya maneno mawili au zaidi ni usemi mkubwa ambao ni sababu ya maneno yote.


