Skip to main content
Global

Sura ya 3 Mazoezi Mapitio

  1. Last updated
  2. Save as PDF
  • Page ID
    175634

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Sura ya Mapitio ya mazoezi

    Grafu ya Ulinganisho wa mstari katika Vigezo viwili

    Plot Pointi katika mfumo wa Kuratibu Rectangular

    Katika mazoezi yafuatayo, njama kila hatua katika mfumo wa kuratibu mstatili.

    1. ⓐ\((−1,−5)\)
    ⓑ\((−3,4)\)
    ⓒ\((2,−3)\)
    ⓓ\((1,\frac{5}{2})\)

    Jibu

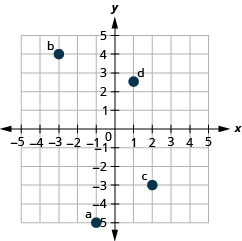
    Takwimu hii inaonyesha pointi zilizopangwa kwenye ndege ya kuratibu x y. Axes x na y huendesha kutoka hasi 5 hadi 5. Hatua iliyoandikwa a ni vitengo 1 upande wa kushoto wa asili na vitengo 5 chini ya asili na iko katika quadrant III. Hatua iliyoandikwa b ni vitengo 3 upande wa kushoto wa asili na vitengo 4 juu ya asili na iko katika quadrant II. Hatua iliyoandikwa c ni vitengo 2 kwa haki ya asili na vitengo 3 chini ya asili na iko katika quadrant IV. Hatua iliyoandikwa d ni kitengo 1 cha haki ya asili na vitengo 2.5 juu ya asili na iko katika quadrant I.

    2. ⓐ\((−2,0)\)
    ⓑ\((0,−4)\)
    ⓒ\((0,5)\)
    ⓓ\((3,0)\)

    Katika mazoezi yafuatayo, tambua ambayo jozi zilizoamriwa ni ufumbuzi wa equations iliyotolewa.

    3. \(5x+y=10\);

    ⓐ\((5,1)\)
    ⓑ\((2,0)\)
    ⓒ\((4,−10)\)

    Jibu

    ⓑ, ⓒ

    4. \(y=6x−2\);

    ⓐ\((1,4)\)
    ⓑ\((13,0)\)
    ⓒ\((6,−2)\)

    Grafu Ulinganisho wa Mstari na Pointi za Kupanga

    Katika mazoezi yafuatayo, grafu kwa pointi za kupanga.

    5. \(y=4x−3\)

    Jibu

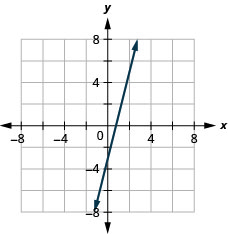
    Takwimu hii inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 1, hasi 7), (0, hasi 3), (1, hasi 1), na (2, 3).

    6. \(y=−3x\)

    7. \(y=\frac{1}{2}x+3\)

    Jibu

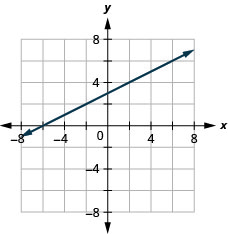
    Takwimu hii inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 6, 0), (0, 3), (2, 4), na (4, 5).

    8. \(y=−\frac{4}{5}|x−1\)

    9. \(x−y=6\)

    Jibu

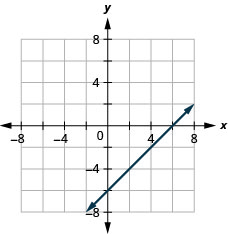
    Takwimu hii inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 1, hasi 7), (0, hasi 6), (3, hasi 3), na (6, 0).

    10. \(2x+y=7\)

    11. \(3x−2y=6\)

    Jibu

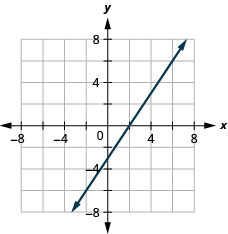
    Takwimu hii inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 2, hasi 6), (0, hasi 3), (2, 0), na (4, 3).

    Grafu mistari ya wima na ya usawa

    Katika mazoezi yafuatayo, graph kila equation.

    12. \(y=−2\)

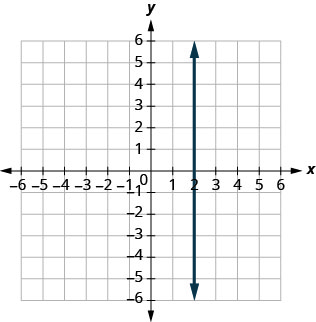
    13. \(x=3\)

    Jibu

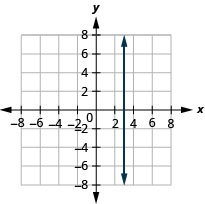
    Takwimu hii inaonyesha mstari wa moja kwa moja wa wima uliowekwa kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (3, hasi 1), (3, 0), na (3, 1).

    Katika mazoezi yafuatayo, grafu kila jozi ya equations katika mfumo huo wa kuratibu mstatili.

    14. \(y=−2x\)na\(y=−2\)

    15. \(y=\frac{4}{3}x\)na\(y=\frac{4}{3}\)

    Jibu

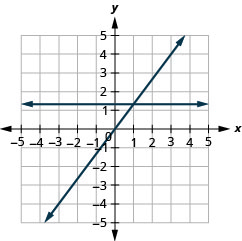
    Takwimu inaonyesha grafu ya mstari wa moja kwa moja usawa na mstari wa moja kwa moja uliopandwa kwenye ndege sawa ya kuratibu x y. Axes x na y huendesha kutoka hasi 5 hadi 5. Mstari wa usawa unaendelea kupitia pointi (0, 4 imegawanywa na 3), (1, 4 imegawanywa na 3), na (2, 4 imegawanywa na 3). Mstari uliopandwa unapitia pointi (0, 0), (1, 4 imegawanywa na 3), na (2, 8 imegawanywa na 3).

    Kupata x- na y- Intercepts

    Katika mazoezi yafuatayo, tafuta x - na y -intercepts.

    16.
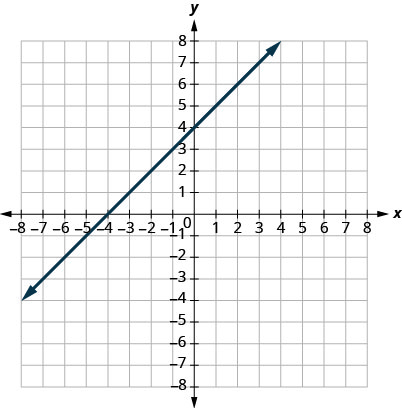
    Takwimu inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Axes x na y huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 6, hasi 2), (hasi 4, 0), (hasi 2, 2), (0, 4), (2, 6), na (4, 8).

    17.
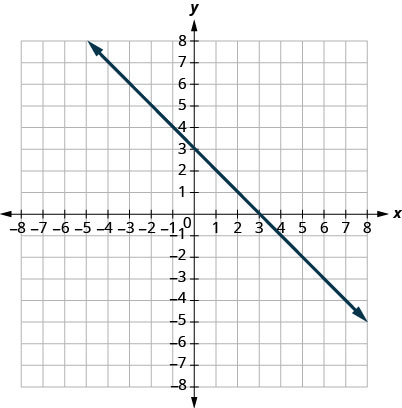
    Takwimu inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Axes x na y huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 2, 5), (hasi 1, 4), (0, 3), (3, 0), na (6, hasi 3).

    Jibu

    \((0,3)(3,0)\)

    Katika mazoezi yafuatayo, pata maingiliano ya kila equation.

    18. \(x−y=−1\)

    19. \(x+2y=6\)

    Jibu

    \((6,0),\space (0,3)\)

    20. \(2x+3y=12\)

    21. \(y=\frac{3}{4}x−12\)

    Jibu

    \((16,0),\space (0,−12)\)

    22. \(y=3x\)

    Grafu Mstari Kutumia Intercepts

    Katika mazoezi yafuatayo, grafu kwa kutumia intercepts.

    23. \(−x+3y=3\)

    Jibu

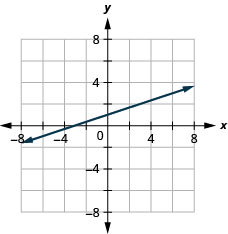
    Takwimu inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Axes x na y huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 3, 0), (0, 1), (3, 2), na (6, 3).

    24. \(x−y=4\)

    25. \(2x−y=5\)

    Jibu

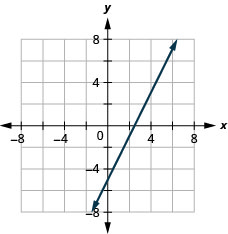
    Takwimu inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Axes x na y huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (0, hasi 5), (1, hasi 3), (2, hasi 1), na (3, 1).

    26. \(2x−4y=8\)

    27. \(y=4x\)

    Jibu

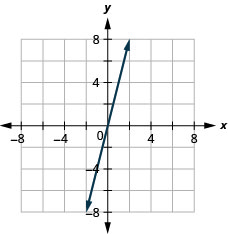
    Takwimu inaonyesha mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Axes x na y huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 1, 4), (0, 0), na (1, hasi 4).

    Mteremko wa Mstari

    Pata mteremko wa Mstari

    Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari umeonyeshwa.

    28.
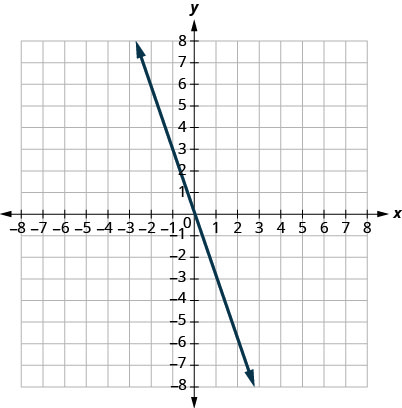
    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari unaendelea kupitia pointi (0, 0) na (1, hasi 3).

    29.
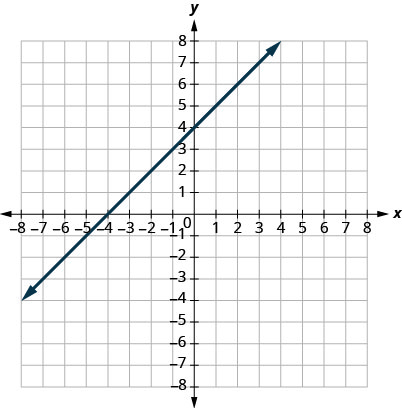
    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari unaendelea kupitia pointi (hasi 4, 0) na (0, 4).

    Jibu

    1

    30.
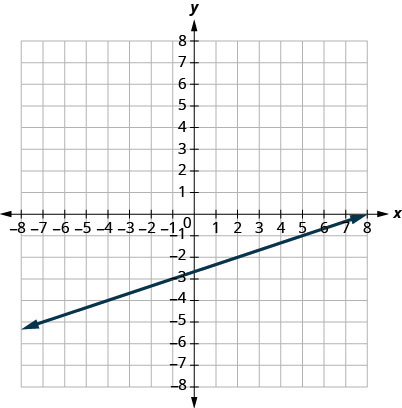
    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari unaendelea kupitia pointi (hasi 4, hasi 4) na (2, hasi 2).

    31.
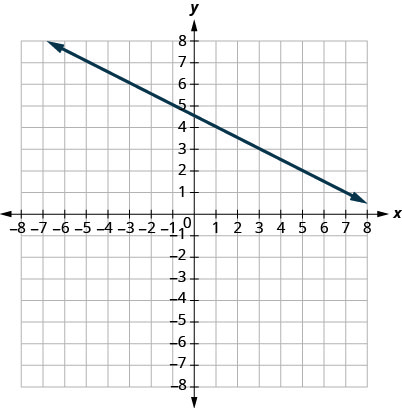
    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari unaendelea kupitia pointi (1, 4) na (5, 2).

    Jibu

    \(−12\)

    Katika mazoezi yafuatayo, tafuta mteremko wa kila mstari.

    32. \(y=2\)

    33. \(x=5\)

    Jibu

    haijafafanuliwa

    34. \(x=−3\)

    35. \(y=−1\)

    Jibu

    0

    Tumia Mfumo wa Slope ili kupata mteremko wa Mstari kati ya Pointi mbili

    Katika mazoezi yafuatayo, tumia fomu ya mteremko ili kupata mteremko wa mstari kati ya kila jozi ya pointi.

    36. \((−1,−1),(0,5)\)

    37. \((3.5),(4,−1)\)

    Jibu

    \(−6\)

    38. \((−5,−2),(3,2)\)

    39. \((2,1),(4,6)\)

    Jibu

    \(52\)

    Grafu Mstari Kutolewa Point na Slope

    Katika mazoezi yafuatayo, grafu kila mstari na hatua iliyotolewa na mteremko.

    40. \((2,−2);\space m=52\)

    41. \((−3,4);\space m=−13\)

    Jibu

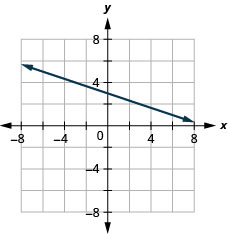
    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 8 hadi 8. Mhimili wa y huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 3, 4) na (0, 3).

    42. \(x\)-kukatiza\(−4; m=3\)

    43. \(y\)-kukatiza\(1; m=−34\)

    Jibu

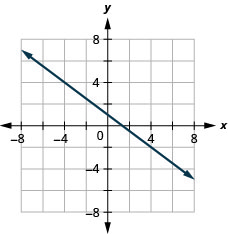
    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 8 hadi 8. Mhimili wa y huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (0, 1) na (4, hasi 2).

    Grafu ya Mstari Kutumia mteremko wake na Ukataji

    Katika mazoezi yafuatayo, tambua mteremko na\(y\) -intercept ya kila mstari.

    44. \(y=−4x+9\)

    45. \(y=53x−6\)

    Jibu

    \(m=53;\space (0,−6)\)

    46. \(5x+y=10\)

    47. \(4x−5y=8\)

    Jibu

    \(m=\frac{4}{5};\space (0,−\frac{8}{5})\)

    Katika mazoezi yafuatayo, graph mstari wa kila equation kwa kutumia mteremko wake na y -intercept.

    48. \(y=2x+3\)

    49. \(y=−x−1\)

    Jibu

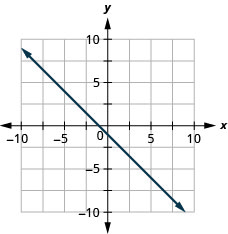
    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (0, hasi 1) na (1, hasi 2).

    50. \(y=−25x+3\)

    51. \(4x−3y=12\)

    Jibu

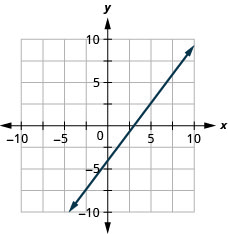
    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (0, hasi 4) na (3, 0).

    Katika mazoezi yafuatayo, tambua njia rahisi zaidi ya kuchora kila mstari.

    52. \(x=5\)

    53. \(y=−3\)

    Jibu

    mstari usio na usawa

    54. \(2x+y=5\)

    55. \(x−y=2\)

    Jibu

    ingilia kati

    56. \(y=22x+2\)

    57. \(y=34x−1\)

    Jibu

    pointi za kupanga njama

    Grafu na Kutafsiri Matumizi ya Slope-Intercept

    58. Katherine ni chef binafsi. equation\(C=6.5m+42\) mifano uhusiano kati ya gharama yake ya kila wiki, C, katika dola na idadi ya chakula, m, kwamba yeye mtumishi.

    ⓐ Kupata gharama Katherine kwa wiki wakati yeye mtumishi hakuna milo.
    ⓑ Kupata gharama kwa wiki wakati yeye mtumishi 14 milo.
    ⓒ Tafsiri mteremko na C -intercept ya equation.
    ⓓ Graph equation.

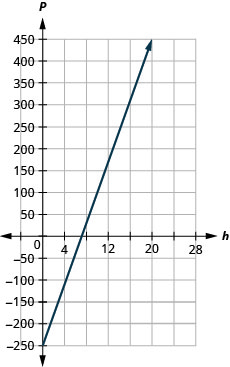
    59. Marjorie inafundisha piano. equation\(P=35h−250\) mfano uhusiano kati ya faida yake ya kila wiki, P, katika dola na idadi ya masomo ya wanafunzi, s, kwamba yeye kufundisha.

    ⓐ Kupata faida Marjorie kwa wiki wakati yeye anafundisha hakuna masomo mwanafunzi.
    ⓑ Pata faida kwa wiki wakati anafundisha masomo ya wanafunzi wa 20.
    ⓒ Tafsiri mteremko na P -intercept ya equation.
    ⓓ Graph equation.

    Jibu

    ⓐ\(−$250\)
    ⓑ\($450\)
    ⓒ mteremko, 35, ina maana kwamba Marjorie ya kila wiki faida, P, kuongezeka kwa $35 kwa kila ziada mwanafunzi somo yeye anafundisha.
    P -intercept ina maana kwamba wakati idadi ya masomo ni 0, Marjorie hupoteza $250.
    ⓓ

    Takwimu hii inaonyesha grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 4 hadi 28. Mhimili wa y huendesha kutoka hasi 250 hadi 450. Mstari unaendelea kupitia pointi (0, hasi 250) na (20, 450).

    Tumia Materemko ya Kutambua Mipangilio ya Sambamba na

    Katika mazoezi yafuatayo, tumia mteremko na\(y\) -intercepts kuamua kama mistari ni sambamba, perpendicular, au wala.

    60. \(4x−3y=−1;\quad y=43x−3\)

    61. \(y=5x−1;\quad 10x+2y=0\)

    Jibu

    hata

    62. \(3x−2y=5;\quad 2x+3y=6\)

    63. \(2x−y=8;\quad x−2y=4\)

    Jibu

    si sambamba

    Pata Equation ya Mstari

    Kupata Equation ya Line Kutokana na mteremko na y -Intercept

    Katika mazoezi yafuatayo, pata usawa wa mstari na mteremko uliopewa na y-intercept. Andika equation katika mteremka-intercept fomu.

    64. Mteremko\(\frac{1}{3}\) na\(y\) -intercept\((0,−6)\)

    65. Mteremko\(−5\) na\(y\) -intercept\((0,−3)\)

    Jibu

    \(y=−5x−3\)

    66. Mteremko\(0\) na\(y\) -intercept\((0,4)\)

    67. Mteremko\(−2\) na\(y\) -intercept\((0,0)\)

    Jibu

    \(y=−2x\)

    Katika mazoezi yafuatayo, pata usawa wa mstari ulioonyeshwa kwenye kila grafu. Andika equation katika mteremka-intercept fomu.

    68.
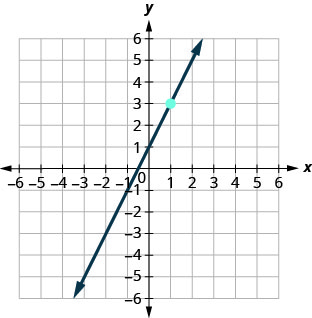
    Takwimu hii ina grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (0, 1), (1, 3), na (2, 5).

    69.
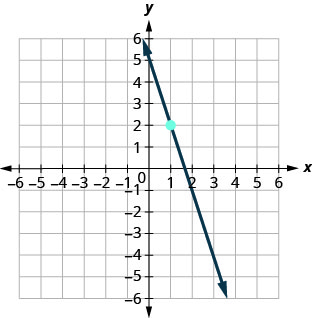
    Takwimu hii ina grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (0, 5), (1, 2), na (2, hasi 1).

    Jibu

    \(y=−3x+5\)

    70.
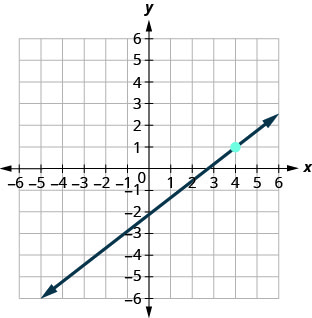
    Takwimu hii ina grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (0, hasi 2), (4, 1), na (8, 4).

    71.
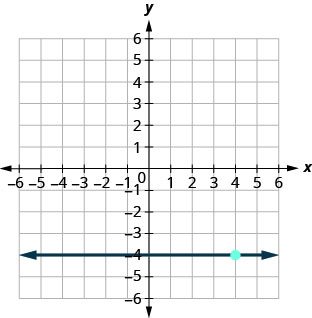
    Takwimu hii ina grafu ya mstari wa moja kwa moja usawa kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (0, hasi 4), (1, hasi 4), na (2, hasi 4).

    Jibu

    \(y=−4\)

    Kupata Equation ya Line Kutokana na mteremko na Point

    Katika mazoezi yafuatayo, pata usawa wa mstari na mteremko uliopewa na una uhakika uliopewa. Andika equation katika mteremka-intercept fomu.

    72. \(m=−\frac{1}{4}\), uhakika\((−8,3)\)

    73. \(m=\frac{3}{5}\), uhakika\((10,6)\)

    Jibu

    \(y=\frac{3}{5}x\)

    74. Mstari wa usawa ulio na\((−2,7)\)

    75. \(m=−2\), uhakika\((−1,−3)\)

    Jibu

    \(y=−2x−5\)

    Kupata Equation ya Line Kutokana Pointi mbili

    Katika mazoezi yafuatayo, pata usawa wa mstari ulio na pointi zilizopewa. Andika equation katika mteremka-intercept fomu.

    76. \((2,10)\)na\((−2,−2)\)

    77. \((7,1)\)na\((5,0)\)

    Jibu

    \(y=\frac{1}{2}x−\frac{5}{2}\)

    78. \((3,8)\)na\((3,−4)\)

    79. \((5,2)\)na\((−1,2)\)

    Jibu

    \(y=2\)

    Pata Equation ya Mstari Sambamba na Line Iliyopewa

    Katika mazoezi yafuatayo, pata usawa wa mstari unaofanana na mstari uliopewa na una uhakika uliopewa. Andika equation katika mteremka-intercept fomu.

    80. mstari\(y=−3x+6\), uhakika\((1,−5)\)

    81. mstari\(2x+5y=−10\), uhakika\((10,4)\)

    Jibu

    \(y=−\frac{2}{5}x+8\)

    82. mstari\(x=4\), uhakika\((−2,−1)\)

    83. mstari\(y=−5\), uhakika\((−4,3)\)

    Jibu

    \(y=3\)

    Kupata Equation ya Line Perpendicular kwa Line Kutokana

    Katika mazoezi yafuatayo, pata equation ya mstari perpendicular kwa mstari uliopewa na ina uhakika fulani. Andika equation katika mteremka-intercept fomu.

    84. mstari\(y=−\frac{4}{5}x+2\), uhakika\((8,9)\)

    85. mstari\(2x−3y=9\), uhakika\((−4,0)\)

    Jibu

    \(y=−\frac{3}{2}x−6\)

    86. mstari\(y=3\), uhakika\((−1,−3)\)

    87. line\(x=−5\) uhakika\((2,1)\)

    Jibu

    \(y=1\)

    Graph Linear kutofautiana katika vigezo viwili

    Thibitisha Ufumbuzi wa Ukosefu wa kutofautiana katika Vigezo viwili

    Katika mazoezi yafuatayo, onyesha kama kila jozi iliyoamriwa ni suluhisho la usawa uliotolewa.

    88. Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(y<x−3\):

    ⓐ\((0,1)\) ⓑ\((−2,−4)\) ⓒ\((5,2)\) ⓓ\((3,−1)\)
    ⓔ\((−1,−5)\)

    89. Kuamua kama kila jozi iliyoamriwa ni suluhisho la kutofautiana\(x+y>4\):

    ⓐ\((6,1)\) ⓑ\((−3,6)\) ⓒ\((3,2)\) ⓓ\((−5,10)\) ⓔ\((0,0)\)

    Jibu

    ⓐ ndiyo ⓑ hapana ⓒ ndiyo ⓓ ndiyo; ⓔ nom

    Tambua Uhusiano Kati ya Ufumbuzi wa Usawa na Grafu yake

    Katika mazoezi yafuatayo, weka usawa unaoonyeshwa na eneo la kivuli.

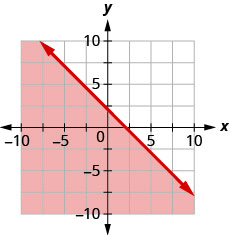
    90. Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=−x+2.\)

    Takwimu hii ina grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Ya x na y axes huendesha kutoka hasi 10 hadi 10. Mstari hutolewa kupitia pointi (0, 2), (1, 1), na (2, 0). Mstari hugawanya ndege ya kuratibu x y katika nusu mbili. Mstari na nusu ya kushoto ya chini ni kivuli nyekundu ili kuonyesha kwamba hii ndio ambapo ufumbuzi wa usawa ni.

    91. Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=\frac{2}{3}x−3\).

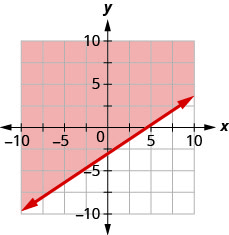
    Takwimu hii ina grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Ya x na y axes huendesha kutoka hasi 10 hadi 10. Mstari hutolewa kupitia pointi (0, hasi 3), (3, hasi 1), na (6, 1). Mstari hugawanya ndege ya kuratibu x y katika nusu mbili. Mstari na nusu ya juu kushoto ni kivuli nyekundu kuonyesha kwamba hii ndio ambapo ufumbuzi wa usawa ni.

    Jibu

    \(y>\frac{2}{3}x−3\)

    92. Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(x+y=−4\).

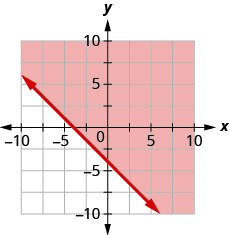
    Takwimu hii ina grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Ya x na y axes huendesha kutoka hasi 10 hadi 10. Mstari hutolewa kupitia pointi (0, hasi 4), (hasi 2, hasi 2), na (hasi 4, 0). Mstari hugawanya ndege ya kuratibu x y katika nusu mbili. Mstari na nusu ya juu ya kulia ni kivuli nyekundu ili kuonyesha kwamba hii ndio ambapo ufumbuzi wa usawa ni.

    93. Andika usawa unaoonyeshwa na eneo la kivuli kwenye grafu na mstari wa mipaka\(x−2y=6\).

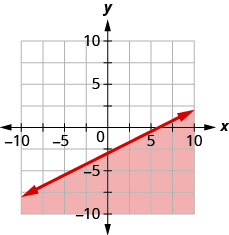
    Takwimu hii ina grafu ya mstari wa moja kwa moja kwenye ndege ya kuratibu x y. Ya x na y axes huendesha kutoka hasi 10 hadi 10. Mstari hutolewa kupitia pointi (0, hasi 3), (2, hasi 2), na (6, 0). Mstari hugawanya ndege ya kuratibu x y katika nusu mbili. Mstari na nusu ya chini ya kulia ni kivuli nyekundu ili kuonyesha kwamba hii ndio ambapo ufumbuzi wa usawa ni.

    Jibu

    \(x−2y\geq 6\)

    Graph Linear kutofautiana katika Vigezo mbili

    Katika mazoezi yafuatayo, grafu kila usawa wa mstari.

    94. Grafu usawa wa mstari\(y>\frac{2}{5}x−4\).

    95. Grafu usawa wa mstari\(y\leq −\frac{1}{4}x+3\).

    Jibu

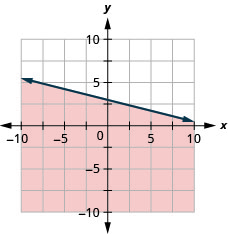
    Takwimu hii ina grafu ya mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Ya x na y axes huendesha kutoka hasi 10 hadi 10. Mstari wa moja kwa moja uliopigwa hutolewa kupitia pointi (0, 3), (4, 2), na (8, 1). Mstari hugawanya ndege ya kuratibu x y katika nusu mbili. Nusu ya chini kushoto ni kivuli nyekundu kuonyesha kwamba hii ndio ambapo ufumbuzi wa usawa ni.

    96. Grafu usawa wa mstari\(x−y\leq 5\).

    97. Grafu usawa wa mstari\(3x+2y>10.\)

    Jibu

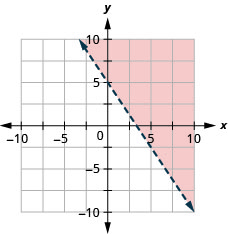
    Takwimu hii ina grafu ya mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Ya x na y axes huendesha kutoka hasi 10 hadi 10. Mstari wa moja kwa moja uliopigwa hutolewa kupitia pointi (0, 5), (2, 2), na (4, hasi 1). Mstari hugawanya ndege ya kuratibu x y katika nusu mbili. Nusu ya juu ya kulia ni kivuli nyekundu ili kuonyesha kwamba hii ndio ambapo ufumbuzi wa usawa ni.

    98. Grafu usawa wa mstari\(y\leq −3x\).

    99. Grafu usawa wa mstari\(y<6.\)

    Jibu

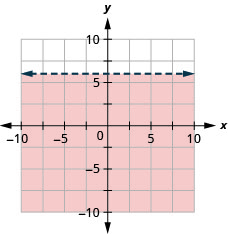
    Takwimu hii ina grafu ya mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Ya x na y axes huendesha kutoka hasi 10 hadi 10. Mstari wa moja kwa moja uliopigwa hutolewa kupitia pointi (0, 6), (1, 6), na (2, 6). Mstari hugawanya ndege ya kuratibu x y katika nusu mbili. Nusu ya chini ni kivuli nyekundu kuonyesha kwamba hii ndio ambapo ufumbuzi wa usawa ni.

    Tatua Maombi kwa kutumia Usawa wa mstari katika Vigezo viwili

    100. Shanthie anahitaji kupata angalau $500 kwa wiki wakati wa mapumziko yake ya majira ya joto ili kulipia chuo. Yeye anafanya kazi mbili. Moja kama mwalimu kuogelea ambayo inalipa $10 saa na nyingine kama Intern katika ofisi ya sheria kwa $25 saa. Shanthie anahitaji saa ngapi kufanya kazi katika kila kazi ili kupata angalau $500 kwa wiki?

    ⓐ Hebu x kuwa idadi ya masaa yeye kazi kufundisha kuogelea na basi y kuwa idadi ya masaa yeye kazi kama Intern. Andika usawa ambayo ingekuwa mfano wa hali hii.
    ⓑ Graph usawa.
    ⓒ Pata jozi tatu zilizoamriwa\((x,y)\) ambazo zitakuwa ufumbuzi wa usawa. Kisha, kueleza nini maana kwa Shanthie.

    101. Ataksushi anahitaji zoezi la kutosha kuchoma\(600\) kalori kila siku. Yeye anapendelea ama kukimbia au baiskeli na nzito\(20\) kalori kwa dakika wakati mbio na\(15\) kalori dakika wakati baiskeli.

    ⓐ Kama x ni idadi ya dakika kwamba Atsushi anaendesha na y ni idadi ya dakika yeye baiskeli, kupata usawa kwamba mifano ya hali.
    ⓑ Graph usawa.
    ⓒ Orodha ya ufumbuzi wa tatu kwa usawa. Ni chaguo gani ambazo ufumbuzi hutoa Atsushi?

    Jibu

    ⓐ\(20x+15y\geq 60020x+15y\geq 600\)
    ⓑ

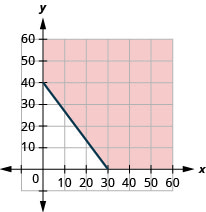
    Takwimu ina mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka 0 hadi 50. Mhimili wa y huendesha kutoka 0 hadi 50. Mstari unaendelea kupitia pointi (0, 40) na (30, 0). Mstari hugawanya ndege ya kuratibu katika nusu mbili. Nusu ya juu ya kulia na mstari ni rangi nyekundu ili kuonyesha kwamba hii ni kuweka suluhisho.

    ⓒ Majibu yatatofautiana.

    Mahusiano na Kazi

    Pata Domain na Upeo wa Uhusiano

    Katika mazoezi yafuatayo, kwa kila uhusiano, ⓐ kupata uwanja wa uhusiano ⓑ kupata aina mbalimbali ya uhusiano.

    102. \({\{(5,−2),\,(5,−4),\,(7,−6),\,(8,−8),\,(9,−10)}\}\)

    103. \({\{(−3,7),\,(−2,3),\,(−1,9), \,(0,−3),\,(−1,8)}\}\)

    Jibu

    ⓐ\(D: {−3, −2, −1, 0}\)
    ⓑ\(R: {7, 3, 9, −3, 8}\)

    Katika zoezi zifuatazo, tumia ramani ya uhusiano na ⓐ orodha ya jozi zilizoamriwa za uhusiano ⓑ kupata uwanja wa uhusiano ⓒ pata mahusiano mbalimbali.

    104. Ramani hapa chini inaonyesha uzito wa mtoto kulingana na umri.

    Takwimu hii inaonyesha meza mbili ambazo kila mmoja ana safu moja. Jedwali upande wa kushoto lina kichwa “Umri (yrs)” na huorodhesha namba 1, 2, 3, 4, 5, 6, na 7. Jedwali upande wa kulia lina kichwa “Uzito (paundi)” na huorodhesha namba 20, 35, 30, 45, 40, 25, na 50. Kuna mishale inayoanzia namba katika meza ya umri na kuelekeza namba katika meza ya uzito. Mshale wa kwanza unatoka 1 hadi 20. Mshale wa pili unatoka 2 hadi 25. Mshale wa tatu unatoka 3 hadi 30. Mshale wa nne unakwenda kutoka 4 hadi 35. Mshale wa tano unatoka 5 hadi 40. Mshale wa sita unakwenda kutoka 6 hadi 45. Mshale wa saba unakwenda kutoka 7 hadi 50.

    Katika zoezi zifuatazo, tumia grafu ya uhusiano na ⓐ orodha ya jozi zilizoamriwa za uhusiano ⓑ kupata uwanja wa uhusiano ⓒ pata mahusiano mbalimbali.

    105.
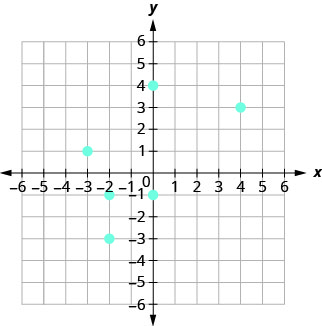
    Takwimu inaonyesha grafu ya pointi fulani kwenye ndege ya kuratibu x y. Ya x na y-axes huendesha kutoka hasi 6 hadi 6. Pointi (hasi 3, 1), (hasi 2, hasi 1), (hasi 2, hasi 3), (0, hasi 1), (0, 4), na (4, 3).

    Jibu

    ⓐ\((4, 3), \,(−2, −3), \,(−2, −1), \,(−3, 1), \,(0, −1), \,(0, 4)\)
    ⓑ\(D: {−3, −2, 0, 4}\)
    ⓒ\(R: {−3, −1, 1, 3, 4}\)

    Kuamua kama Uhusiano ni Kazi

    Katika mazoezi yafuatayo, tumia seti ya jozi zilizoamriwa ili ⓐ kuamua kama uhusiano ni kazi ⓑ kupata uwanja wa uhusiano ⓒ kupata mahusiano mbalimbali.

    106. \({\{(9,−5),\,(4,−3),\,(1,−1),\,(0,0),\,(1,1),\,(4,3),\,(9,5)}\}\)

    107. \({\{(−3,27),\,(−2,8),\,(−1,1),\,(0,0),\,(1,1),\,(2,8),\,(3,27)}\}\)

    Jibu

    ⓐ ndiyo ⓑ\({−3, −2, −1, 0, 1, 2, 3}\)
    ⓒ\({0, 1, 8, 27}\)

    Katika mazoezi yafuatayo, tumia ramani ya ⓐ kuamua kama uhusiano ni kazi ⓑ kupata uwanja wa kazi ⓒ kupata kazi mbalimbali.

    108.
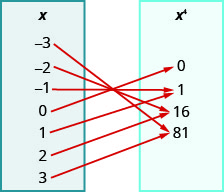
    Takwimu hii inaonyesha meza mbili ambazo kila mmoja ana safu moja. Jedwali upande wa kushoto lina kichwa “x” na huorodhesha namba hasi 3, hasi 2, hasi 1, 0, 1, 2, na 3. Jedwali upande wa kulia lina kichwa “x kwa nguvu ya nne” na inaorodhesha namba 0, 1, 16, na 81. Kuna mishale kuanzia kwa idadi katika meza x na kuelekeza kuelekea namba katika x kwa meza ya nne nguvu. Mshale wa kwanza unatoka hasi 3 hadi 81. Mshale wa pili huenda kutoka hasi 2 hadi 16. Mshale wa tatu unatoka hasi 1 hadi 1. Mshale wa nne unakwenda kutoka 0 hadi 0. Mshale wa tano unatoka 1 hadi 1. Mshale wa sita unakwenda kutoka 2 hadi 16. Mshale wa saba unatoka 3 hadi 81.

    109.
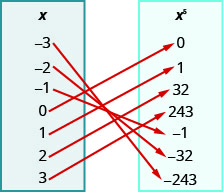
    Takwimu hii inaonyesha meza mbili ambazo kila mmoja ana safu moja. Jedwali upande wa kushoto lina kichwa “x” na huorodhesha namba hasi 3, hasi 2, hasi 1, 0, 1, 2, na 3. Jedwali upande wa kulia lina kichwa “x hadi nguvu ya tano” na inaorodhesha namba 0, 1, 32, 243, hasi 1, hasi 32, na hasi 243. Kuna mishale kuanzia kwa idadi katika meza x na kuelekeza kuelekea namba katika x kwa meza ya tano nguvu. Mshale wa kwanza unatoka hasi 3 hadi hasi 243. Mshale wa pili huenda kutoka hasi 2 hadi hasi 32. Mshale wa tatu unatoka hasi 1 hadi 1. Mshale wa nne unakwenda kutoka 0 hadi 0. Mshale wa tano unatoka 1 hadi 1. Mshale wa sita unakwenda kutoka 2 hadi 32. Mshale wa saba unatoka 3 hadi 243.

    Jibu

    ⓐ\({−3, −2, −1, 0, 1, 2, 3}\)
    ⓑ\({−3, −2, −1, 0, 1, 2, 3}\)
    ⓒ\({−243, −32, −1, 0, 1, 32, 243}\)

    Katika mazoezi yafuatayo, onyesha kama kila equation ni kazi.

    110. \(2x+y=−3\)

    111. \(y=x^2\)

    Jibu

    ndiyo

    112. \(y=3x−5\)

    113. \(y=x^3\)

    Jibu

    ndiyo

    114. \(2x+y2=4\)

    Pata Thamani ya Kazi

    Katika mazoezi yafuatayo, tathmini kazi:

    ⓐ\(f(−2)\) ⓑ\(f(3)\) ⓒ\(f(a)\).

    115. \(f(x)=3x−4\)

    Jibu

    ⓐ\(f(−2)=−10\) ⓑ\(f(3)=5\) ⓒ\(f(a)=3a−4\)

    116. \(f(x)=−2x+5\)

    117. \(f(x)=x^2−5x+6\)

    Jibu

    ⓐ\(f(−2)=20\) ⓑ\(f(3)=0\) ⓒ\(f(a)=a^2−5a+6\)

    118. \(f(x)=3x^2−2x+1\)

    Katika mazoezi yafuatayo, tathmini kazi.

    119. \(g(x)=3x2−5x;\space g(2)\)

    Jibu

    \(2\)

    120. \(F(x)=2x2−3x+1;\space F(−1)\)

    121. \(h(t)=4|t−1|+2;\space h(t)=4\)

    Jibu

    \(18\)

    122. \(f(x)=x+2x−1;\space f(3)\)

    Grafu ya Kazi

    Tumia Mtihani wa mstari wa Wima

    Katika mazoezi yafuatayo, onyesha kama kila grafu ni grafu ya kazi.

    123.
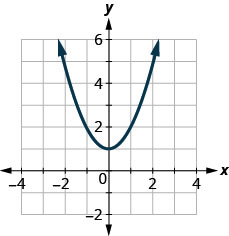
    Takwimu ina kazi ya mraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 2 hadi 10. Parabola hupitia pointi (hasi 2, 5), (hasi 1, 2), (0, 1), (1, 2), na (2, 5). Hatua ya chini kabisa kwenye grafu ni (0, 1).

    Jibu

    ndiyo

    124.
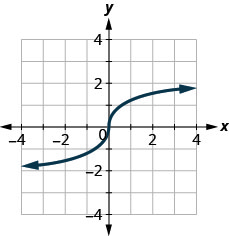
    Takwimu ina kazi ya umbo la s iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Curve hupitia pointi (hasi 1, hasi 1), (0, 0), na (1, 1).

    125.
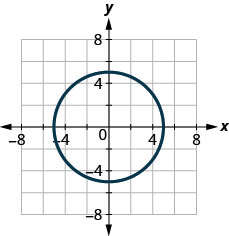
    Takwimu ina mduara uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mzunguko unaendelea kupitia pointi (hasi 5, 0), (5, 0), (0, hasi 5), na (0, 5).

    Jibu

    hapana

    126.
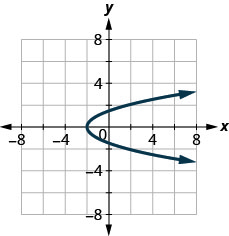
    Takwimu ina ufunguzi wa parabola kwa haki iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 2 hadi 10. Parabola hupitia pointi (hasi 2, 0), (hasi 1, 1), (hasi 1, hasi 1), (2, 2), na (2, hasi 2). Hatua ya kushoto zaidi kwenye grafu ni (hasi 2, 0).

    127.
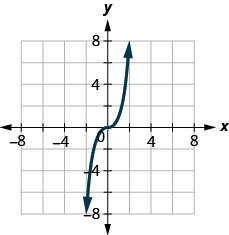
    Takwimu ina kazi ya mchemraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari wa mviringo unapitia pointi (hasi 1, hasi 1), (0, 0), na (1, 1).

    Jibu

    ndiyo

    128.
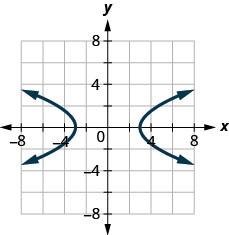
    Takwimu ina mistari miwili iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari wa mviringo upande wa kushoto unaendelea kupitia pointi (hasi 3, 0), (hasi 4, 2), na (hasi 4, hasi 2). Mstari wa mviringo upande wa kulia unaendelea kupitia pointi (3, 0), (4, 2), na (4, hasi 2).

    129.
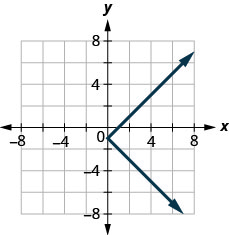
    takwimu ina sideways kabisa thamani kazi graphed juu ya x y-kuratibu ndege. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari hupiga hatua (0, hasi 1) na huenda kwa haki. Mstari unaendelea kupitia pointi (1, 0), (1, hasi 2), (2, 1), na (2, hasi 3).

    Jibu

    hapana

    Tambua Grafu za Kazi za Msingi

    Katika mazoezi yafuatayo, ⓐ grafu kila kazi ⓑ hali ya kikoa na upeo wake. Andika kikoa na upeo katika maelezo ya muda.

    130. \(f(x)=5x+1\)

    131. \(f(x)=−4x−2\)

    Jibu

    ⓐ

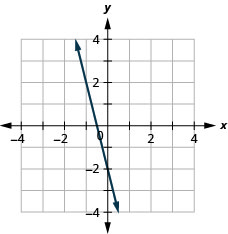
    Takwimu ina kazi ya mstari iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari unaendelea kupitia pointi (hasi 2, 6), (hasi 1, 2), na (0, hasi 2).

    ⓑ\(D: (-\inf ,\inf ), R: (-\inf ,\inf )\)

    132. \(f(x)=\frac{2}{3}x−1\)

    133. \(f(x)=−6\)

    Jibu

    ⓐ

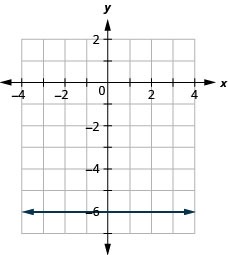
    Takwimu ina kazi ya mara kwa mara iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 8 hadi 4. Mstari unaendelea kupitia pointi (0, hasi 6), (1, hasi 6), na (2, hasi 6).

    ⓑ\(D: (-\inf ,\inf ), R: (-\inf ,\inf )\)

    134. \(f(x)=2x\)

    135. \(f(x)=3x^2\)

    Jibu

    ⓐ

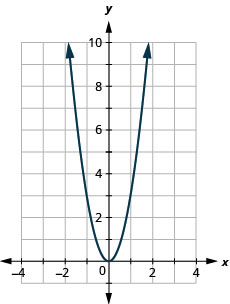
    Takwimu ina kazi ya mraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 2 hadi 10. Parabola hupitia pointi (hasi 1, 3), (0, 0), na (1, 3). Hatua ya chini kabisa kwenye grafu ni (0, 0).

    ⓑ\(D: (-\inf ,\inf ), R: (-\inf ,0]\)

    136. \(f(x)=−12x^2\)

    137. \(f(x)=x^2+2\)

    Jibu

    ⓐ

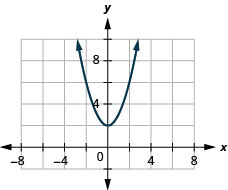
    Takwimu ina kazi ya mraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 4 hadi 8. Parabola hupitia pointi (hasi 2, 6), (hasi 1, 3), (0, 2), (1, 3), na (2, 6). Hatua ya chini kabisa kwenye grafu ni (0, 2).

    ⓑ\(D: (-\inf ,\inf ), R: (-\inf ,\inf )\)

    138. \(f(x)=x^3−2\)

    139. \(f(x)=\sqrt{x+2}\)

    Jibu

    ⓐ

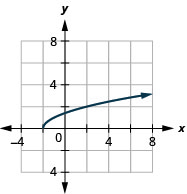
    Takwimu ina kazi ya mizizi ya mraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 4 hadi 8. Mhimili wa y huendesha kutoka hasi 2 hadi 10. Mstari wa nusu huanza kwa hatua (hasi 2, 0) na huenda kupitia pointi (hasi 1, 1) na (2, 2).

    ⓑ\(D: [−2,−2, \inf ), \space R: [0,\inf )\)

    140. \(f(x)=−|x|\)

    141. \(f(x)=|x|+1\)

    Jibu

    ⓐ

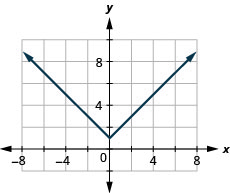
    Takwimu ina kazi ya thamani kamili iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 2 hadi 10. Vertex iko kwenye hatua (0, 1). Mstari unaendelea kupitia pointi (hasi 1, 2) na (1, 2).

    ⓑ\(D: (-\inf ,\inf ), \space R: [1,\inf )\)

    Soma Taarifa kutoka kwa Graph ya Kazi

    Katika mazoezi yafuatayo, tumia grafu ya kazi ili kupata uwanja na upeo wake. Andika kikoa na upeo katika maelezo ya muda

    142.
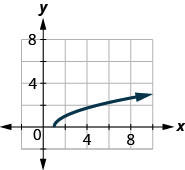
    Takwimu ina kazi ya mizizi ya mraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka 0 hadi 10. Mhimili wa y huendesha kutoka 0 hadi 10. Mstari wa nusu huanza kwa hatua (1, 0) na huenda kupitia pointi (2, 1) na (5, 2).

    143.
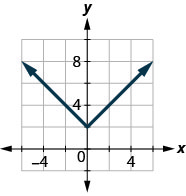
    Takwimu ina kazi ya thamani kamili iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 2 hadi 10. Vertex iko kwenye hatua (0, 2). Mstari unaendelea kupitia pointi (hasi 1, 3) na (1, 3).

    Jibu

    \(D: (-\inf ,\inf ), R: [2,\inf )\)

    144.
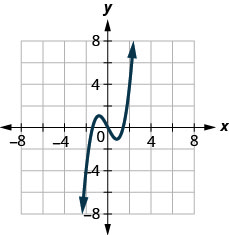
    Takwimu ina kazi ya ujazo iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari wa mviringo unapitia pointi (hasi 2, hasi 4), (0, 0), na (2, 4).

    Katika mazoezi yafuatayo, tumia grafu ya kazi ili kupata maadili yaliyoonyeshwa.

    145.
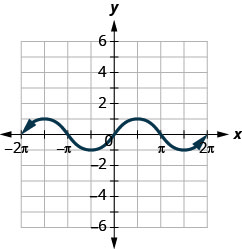
    Takwimu hii ina mstari wa mviringo wa wavy uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka mara 2 hasi pi hadi mara 2 pi. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Sehemu ya mstari wa mviringo hupitia pointi (hasi 2 mara pi, 0), (hasi 3 imegawanywa na mara 2 pi, 1), (hasi pi, 0), (hasi 1 imegawanywa na mara 2 pi, hasi 1), (1 imegawanywa na mara 2 pi, 0), (3 imegawanywa na mara 2 pi, hasi 1), na (mara 2 pi, 0). Pointi (hasi 3 imegawanywa na mara 2 pi, 1) na (1 imegawanywa na mara 2 pi, 1) ni pointi za juu kwenye grafu. Pointi (hasi 1 imegawanywa na mara 2 pi, hasi 1) na (3 imegawanywa na mara 2 pi, hasi 1) ni pointi za chini kabisa kwenye grafu. Mfano unaendelea kwa kiasi kikubwa upande wa kushoto na wa kulia.

    ⓐ Tafuta\(f(0)\).
    ⓑ Tafuta\(f(12\pi )\).
    ⓒ Tafuta\(f(−32\pi )\).
    ⓓ Kupata maadili kwa\(x\) wakati\(f(x)=0\).
    ⓔ Kupata\(x\) -intercepts.
    ⓕ Pata\(y\) -intercept (s).
    ⓖ Pata uwanja. Andika kwa ubaguzi wa muda.
    ⓗ Pata upeo. Andika kwa ubaguzi wa muda.

    Jibu

    ⓐ\(f(x)=0\) ⓑ\(f(\pi /2)=1\)
    ⓒ\(f(−3\pi /2)=1\) ⓓ\(f(x)=0\) for\(x=−2\pi ,−\pi ,0,\pi ,2\pi\)
    ⓔ\((−2\pi ,0), (−\pi ,0), (0,0), (\pi ,0), (2\pi ,0)\) ⓕ\((0,0)\)
    ⓖ\([−2\pi ,2\pi ]\) ⓗ\([−1,1]\)

    146.
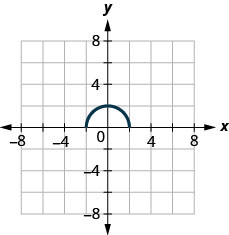
    Takwimu ina mduara wa nusu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Sehemu ya mstari wa mstari huanza kwa hatua (hasi 2, 0). Mstari unaendelea kupitia hatua (0, 2) na kuishia kwa uhakika (2, 0). Hatua (0, 2) ni hatua ya juu kwenye grafu.

    ⓐ Tafuta\(f(0)\).
    ⓑ Kupata maadili kwa\(x\) wakati\(f(x)=0\).
    ⓒ Kupata\(x\) -intercepts.
    ⓓ Pata\(y\) -intercept (s).
    ⓔ Pata uwanja. Andika kwa ubaguzi wa muda.
    ⓕ Pata upeo. Andika kwa ubaguzi wa muda.

    Mazoezi mtihani

    1. Panda kila hatua katika mfumo wa kuratibu mstatili.

    ⓐ\((2,5)\)
    ⓑ\((−1,−3)\)
    ⓒ\((0,2)\)
    ⓓ\((−4,32)\)
    ⓔ\((5,0)\)

    Jibu

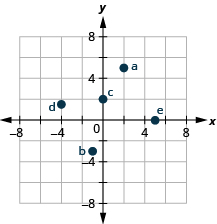
    Takwimu hii inaonyesha pointi zilizopangwa kwenye ndege ya kuratibu x y. Ya x na y axes huendesha kutoka hasi 10 hadi 10. uhakika kinachoitwa a ni 2 vitengo na haki ya asili na vitengo 5 juu ya asili na iko katika roboduara I. uhakika kinachoitwa b ni 1 kitengo upande wa kushoto wa asili na vitengo 3 chini ya asili na iko katika roboduara III. Hatua iliyoandikwa c ni vitengo 2 juu ya asili na iko kwenye mhimili wa y. Hatua iliyoandikwa d ni vitengo 4 upande wa kushoto wa asili na vitengo 1.5 juu ya asili na iko katika quadrant II. Hatua iliyoandikwa e ni vitengo 5 kwa haki ya asili na iko kwenye mhimili wa x.

    2. Ni ipi kati ya jozi zilizopewa zilizoamriwa ni ufumbuzi wa equation\(3x−y=6\)?

    ⓐ\((3,3)\) ⓑ\((2,0)\) ⓒ\((4,−6)\)

    3. Pata mteremko wa kila mstari umeonyeshwa.

    ⓐ

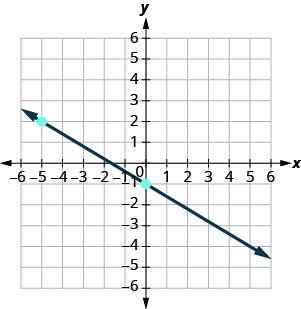
    Takwimu ina mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (hasi 5, 2) (0, hasi 1), na (5, hasi 4).

    ⓑ

    Takwimu ina mstari wa wima wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (2, 0) (2, hasi 1), na (2, 1).
    Jibu

    ⓐ\(−\frac{3}{5}\) ⓑ haijafafanuliwa

    4. Pata mteremko wa mstari kati ya pointi\((5,2)\) na\((−1,−4)\).

    5. Grafu mstari na mteremko\(\frac{1}{2}\) ulio na uhakika\((−3,−4)\).

    Jibu

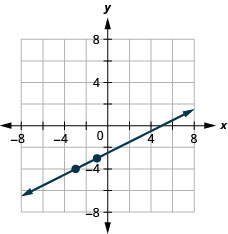
    Takwimu ina mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (hasi 3, hasi 4) (hasi 1, hasi 3), na (1, hasi 2).

    6. Kupata intercepts ya\(4x+2y=−8\) na grafu.

    Grafu mstari kwa kila moja ya equations zifuatazo.

    7. \(y=\frac{5}{3}x−1\)

    Jibu

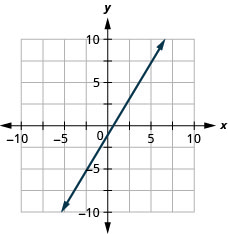
    Takwimu ina mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (hasi 3, hasi 6) (0, hasi 1), na (3, 4).

    8. \(y=−x\)

    9. \(y=2\)

    Jibu

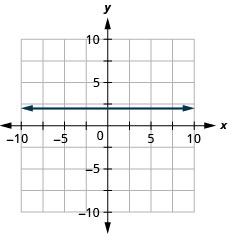
    Takwimu ina mstari wa usawa wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (hasi 1, 2) (0, 2), na (1, 2).

    Kupata equation ya kila mstari. Andika equation katika fomu ya mteremka-intercept.

    10. mteremko\(−\frac{3}{4}\) na\(y\) -intercept\((0,−2)\)

    11. \(m=2\), uhakika\((−3,−1)\)

    Jibu

    \(y=2x+5\)

    12. zenye\((10,1)\) na\((6,−1)\)

    13. perpendicular kwa mstari\(y=\frac{5}{4}x+2\), iliyo na uhakika\((−10,3)\)

    Jibu

    \(y=−\frac{4}{5}x−5\)

    14. Andika usawa unaoonyeshwa na grafu na mstari wa mipaka\(y=−x−3\).

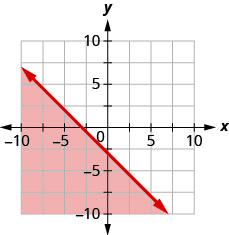
    Takwimu ina mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (hasi 3, 0), (0, hasi 3), na (1, hasi 4). Mstari hugawanya ndege ya kuratibu katika nusu mbili. Nusu ya kushoto ya chini na mstari ni rangi nyekundu ili kuonyesha kwamba hii ni kuweka suluhisho.

    Graph kila usawa linear.

    15. \(y>\frac{3}{2}x+5\)

    Jibu

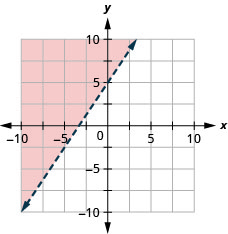
    Takwimu ina mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 10 hadi 10. Mhimili wa y huendesha kutoka hasi 10 hadi 10. Mstari unaendelea kupitia pointi (hasi 2, 2), (0, 5), na (2, 8). Mstari hugawanya ndege ya kuratibu katika nusu mbili. Nusu ya kushoto ya juu ni rangi nyekundu ili kuonyesha kwamba hii ni kuweka suluhisho.

    16. \(x−y\geq −4\)

    17. \(y\leq −5x\)

    Jibu

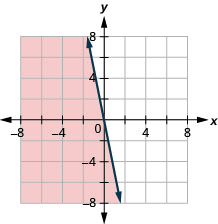
    Takwimu ina mstari wa moja kwa moja uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 8 hadi 8. Mhimili wa y huendesha kutoka hasi 8 hadi 8. Mstari unaendelea kupitia pointi (hasi 1, 5), (0, 0), na (1, hasi 5). Mstari hugawanya ndege ya kuratibu katika nusu mbili. Nusu ya kushoto ya chini na mstari ni rangi nyekundu ili kuonyesha kwamba hii ni kuweka suluhisho.

    18. Hiro anafanya kazi za muda wa sehemu mbili ili kupata pesa za kutosha ili kukidhi majukumu yake ya angalau $450 kwa wiki. Kazi yake katika maduka hulipa $10 saa na kazi yake ya utawala msaidizi kwenye chuo inalipa $15 saa. Hiro anahitaji saa ngapi kufanya kazi katika kila kazi ili kupata angalau $450?

    ⓐ Hebu x kuwa idadi ya masaa yeye anafanya kazi katika maduka na basi y kuwa idadi ya masaa yeye kazi kama msaidizi wa utawala. Andika usawa ambayo ingekuwa mfano wa hali hii.
    ⓑ Graph usawa.
    ⓒ Pata jozi tatu zilizoamriwa\((x,y)\) ambazo zitakuwa ufumbuzi wa usawa. Kisha kueleza nini maana yake kwa Hiro.

    19. Tumia seti ya jozi zilizoamriwa ⓐ kuamua kama uhusiano ni kazi, ⓑ kupata uwanja wa uhusiano, na ⓒ kupata aina mbalimbali ya uhusiano.

    \ ({\ {(-3,27), (-2,8), (-1,1), (0,0),
    (1,1), (2,8), (3,27)}\}\)

    Jibu

    ⓐ ndiyo ⓑ\({\{−3,−2,−1,0,1,2,3}\}\) ⓒ\({\{0, 1, 8, 27}\}\)

    20. Tathmini kazi: ⓐ\(f(−1)\) ⓑ\(f(2)\) ⓒ\(f(c)\).

    \(f(x)=4x^2−2x−3\)

    21. Kwa\(h(y)=3|y−1|−3\), tathmini\(h(−4)\).

    Jibu

    \(12\)

    22. Kuamua kama grafu ni grafu ya kazi. Eleza jibu lako.

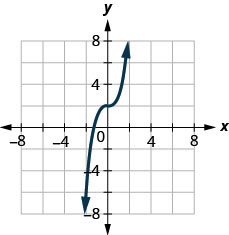
    Takwimu ina kazi ya mchemraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Mstari wa mviringo unapitia pointi (hasi 1, 1), (0, 2), na (1, 3).

    Katika mazoezi yafuatayo, ⓐ grafu kila kazi ⓑ hali ya kikoa na upeo wake.
    Andika kikoa na upeo katika maelezo ya muda.

    23. \(f(x)=x^2+1\)

    Jibu

    ⓐ

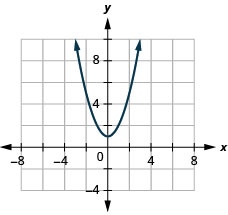
    Takwimu ina kazi ya mraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 2 hadi 10. Parabola hupitia pointi (hasi 2, 5), (hasi 1, 2), (0, 1), (1, 2), na (2, 5). Hatua ya chini kabisa kwenye grafu ni (0, 1).

    ⓑ\(D: (-\inf ,\inf ), R: [1,\inf )\)

    24. \(f(x)=\sqrt{x+1}\)

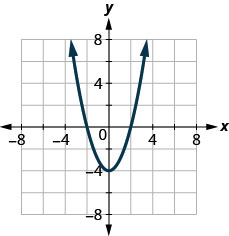
    Takwimu ina kazi ya mraba iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-huendesha kutoka hasi 6 hadi 6. Mhimili wa y huendesha kutoka hasi 6 hadi 6. Parabola hupitia pointi (hasi 2, 0), (hasi 1, hasi 3), (0, hasi 4), (1, hasi 3), na (2, 0). Hatua ya chini kabisa kwenye grafu ni (0, hasi 4).

    ⓑ Kupata\(y\) -intercepts.
    ⓒ Tafuta\(f(−1)\).
    ⓓ Tafuta\(f(1)\).
    ⓔ Pata uwanja. Andika kwa ubaguzi wa muda.
    ⓕ Pata upeo. Andika kwa ubaguzi wa muda.

    Jibu

    ⓐ\(x=−2,2\) ⓑ\(y=−4\)
    ⓒ\(f(−1)=−3\) ⓓ\(f(1)=−3\)
    ⓔ\(D: (-\inf ,\inf )\) ⓕ\(R: [−4, \inf)\)