Skip to main content
Global

2.7: Kutatua Usawa wa Kiwanja

  1. Last updated
  2. Save as PDF
  • Page ID
    176788

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kutatua usawa kiwanja na “na”
    • Kutatua usawa kiwanja na “au”
    • Tatua programu na kutofautiana kwa kiwanja

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kurahisisha:\(\frac{2}{5}(x+10)\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    2. Kurahisisha:\(−(x−4)\).
      Ikiwa umekosa tatizo hili, tathmini [kiungo].

    Kutatua Usawa wa Kiwanja na “na”

    Sasa kwa kuwa tunajua jinsi ya kutatua usawa wa mstari, hatua inayofuata ni kuangalia usawa wa kiwanja. Ukosefu wa usawa wa kiwanja unajumuisha kutofautiana mbili zinazounganishwa na neno “na” au neno “au.” Kwa mfano, zifuatazo ni kutofautiana kwa kiwanja.

    \[\begin{array} {lll} {x+3>−4} &{\text{and}} &{4x−5\leq 3} \\ {2(y+1)<0} &{\text{or}} &{y−5\geq −2} \\ \end{array} \nonumber\]

    KIWANJA USAWA

    Ukosefu wa usawa wa kiwanja unajumuisha kutofautiana mbili zinazounganishwa na neno “na” au neno “au.”

    Ili kutatua usawa wa kiwanja inamaanisha kupata maadili yote ya kutofautiana ambayo hufanya usawa wa kiwanja kuwa taarifa ya kweli. Sisi kutatua kutofautiana kiwanja kwa kutumia mbinu sawa sisi kutumika kutatua usawa linear. Sisi kutatua kila usawa tofauti na kisha kufikiria ufumbuzi mbili.

    Ili kutatua usawa wa kiwanja na neno “na,” tunatafuta namba zote zinazofanya kutofautiana kwa kweli. Ili kutatua usawa wa kiwanja na neno “au,” tunatafuta namba zote zinazofanya usawa wa kweli.

    Hebu tuanze na kutofautiana kwa kiwanja na “na.” Suluhisho letu litakuwa namba ambazo ni ufumbuzi wa kutofautiana kwa wote unaojulikana kama makutano ya kutofautiana mbili. Fikiria makutano ya mitaa miwili-sehemu ambapo mitaa huingilia—ni ya mitaa yote miwili.

    Takwimu ni mfano wa mitaa miwili na makutano yao yamevuliwa.

    Ili kupata suluhisho la usawa wa “na” wa kiwanja, tunaangalia grafu za kila usawa na kisha kupata namba ambazo ni za grafu zote mbili-ambapo grafu zinaingiliana.

    Kwa usawa wa kiwanja\(x>−3\) na\(x\leq 2\), sisi grafu kila usawa. Sisi kisha kuangalia kwa ambapo grafu “kuingiliana”. Nambari ambazo zimefunikwa kwenye grafu zote mbili, zitakuwa kivuli kwenye grafu ya suluhisho la usawa wa kiwanja. Angalia Kielelezo\(\PageIndex{1}\).

    Takwimu inaonyesha grafu ya x ni kubwa kuliko hasi 3 na mabano ya kushoto kwa hasi 3 na kivuli kwa haki yake, grafu ya x ni chini ya au sawa na 2 na bracket saa 2 na kivuli upande wa kushoto, na grafu ya x ni kubwa kuliko hasi 3 na x ni chini ya au sawa na 2 na mabano ya kushoto katika hasi 3 na mabano sahihi katika 2 na shading kati ya hasi 3 na 2. Hasi 3 na 2 ni alama na mistari kwenye kila mstari wa nambari.
    Kielelezo\(\PageIndex{1}\)

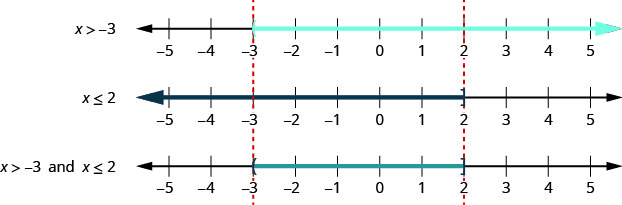
    Tunaweza kuona kwamba idadi kati ya\(−3\) na\(2\) ni kivuli juu ya wote wa grafu mbili za kwanza. Wao kisha kuwa kivuli kwenye grafu ya suluhisho.

    Nambari\(−3\) haipatikani kwenye grafu ya kwanza na hivyo kwa kuwa haijavuliwa kwenye grafu zote mbili, haijaingizwa kwenye grafu ya suluhisho.

    Nambari mbili ni kivuli kwenye grafu zote za kwanza na za pili. Kwa hiyo, ni kivuli kwenye grafu ya suluhisho.

    Hii ndio jinsi tutakavyoonyesha suluhisho letu katika mifano inayofuata.

    Mfano\(\PageIndex{1}\)

    Kutatua\(6x−3<9\) na\(2x+7\geq 3\). Grafu suluhisho na uandike suluhisho katika maelezo ya muda.

    Jibu
      \(6x−3<9\) na \(2x+9\geq 3\)
    Hatua ya 1. Kutatua kila
    kukosekana kwa usawa.    		 \(6x−3<9\)   \(2x+9\geq 3\)
      \(6x<12\)   \(2x\geq −6\)
      \(x<2\) na \(x\geq −3\)
    Hatua ya 2. Grafu kila suluhisho. Kisha grafu namba zinazofanya kutofautiana kwa kweli. Grafu ya mwisho itaonyesha namba zote zinazofanya kutofautiana kwa kweli - namba zimefunikwa kwenye grafu mbili za kwanza. .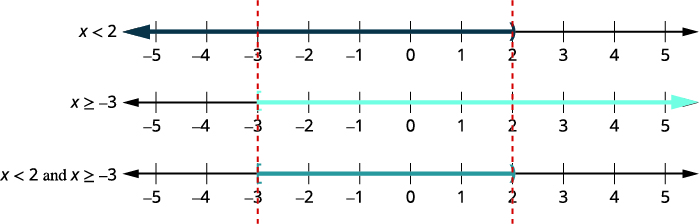
    Hatua ya 3. Andika suluhisho katika maelezo ya muda. \([−3,2)\)
    Nambari zote zinazofanya kutofautiana kwa kweli ni suluhisho la usawa wa kiwanja.
    Mfano\(\PageIndex{2}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(4x−7<9\) na\(5x+8\geq 3\).

    Jibu

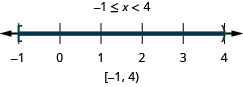
    Suluhisho ni hasi 1 ni chini ya au sawa na x ambayo ni chini ya 4. Katika mstari wa nambari huonyeshwa kwa mduara uliofungwa kwenye hasi 1 na mduara wazi saa 4 na kivuli kati ya miduara iliyofungwa na ya wazi. Uthibitishaji wake wa muda ni hasi 1 hadi 4 ndani ya bracket na mabano.

    Mfano\(\PageIndex{3}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(3x−4<5\) na\(4x+9\geq 1\).

    Jibu

    Suluhisho ni hasi 2 ni chini ya au sawa na x ambayo ni chini ya 3. Katika mstari wa nambari huonyeshwa kwa mduara uliofungwa kwenye hasi 2 na mduara wazi saa 3 na kivuli kati ya miduara iliyofungwa na ya wazi. Uthibitishaji wake wa muda ni hasi 2 hadi 3 ndani ya bracket na mabano.

    KUTATUA USAWA KIWANJA NA “NA.”
    1. Kutatua kila usawa.
    2. Grafu kila suluhisho. Kisha grafu namba zinazofanya kutofautiana kwa kweli.
      Grafu hii inaonyesha suluhisho la usawa wa kiwanja.
    3. Andika suluhisho katika maelezo ya muda.
    Mfano\(\PageIndex{4}\)

    Kutatua\(3(2x+5)\leq 18\) na\(2(x−7)<−6\). Grafu suluhisho na uandike suluhisho katika maelezo ya muda.

    Jibu
      \(3(2x+5)\leq 18\) na \(2(x−7)<−6\)
    Kutatua kila
    kukosekana kwa usawa.    		 \(6x+15\leq 18\)   \(2x−14<−6\)
      \(6x\leq 3\)   \(2x<8\)
      \(x\leq \frac{1}{2}\) na \(x<4\)
    Grafu kila
    suluhisho.    		 .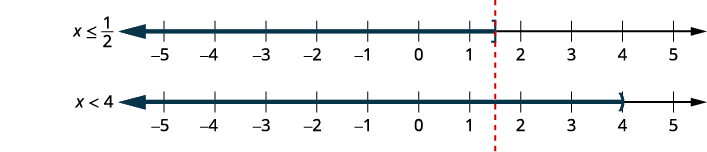
    Grafu namba
    zinazofanya
    kutofautiana kwa kweli.    		 .
    Andika suluhisho
    katika maelezo ya muda.    		 \((−\infty, \frac{1}{2}]\)
    Mfano\(\PageIndex{5}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(2(3x+1)\leq 20\) na\(4(x−1)<2\).

    Jibu

    Suluhisho ni x ni chini ya nusu tatu. Kwenye mstari wa nambari huonyeshwa kwa mduara wazi kwa nusu tatu na shading upande wa kushoto. Nukuu yake ya muda ni infinity hasi kwa nusu tatu ndani ya mabano.

    Mfano\(\PageIndex{6}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(5(3x−1)\leq 10\) na\(4(x+3)<8\).

    Jibu

    Suluhisho ni x ni chini ya hasi 1. Kwenye mstari wa nambari huonyeshwa kwa mduara wazi saa 1 na kivuli upande wa kushoto. Muda wake nukuu ni infinity hasi kwa hasi 1 ndani ya mabano.

    Mfano\(\PageIndex{7}\)

    Kutatua\(\frac{1}{3}x−4\geq −2\) na\(−2(x−3)\geq 4\). Grafu suluhisho na uandike suluhisho katika maelezo ya muda.

    Jibu
      \(\frac{1}{3}x−4\geq −2\) na \(−2(x−3)\geq 4\)
    Kutatua kila usawa. \(\frac{1}{3}x−4\geq −2\)   \(−2x+6\geq 4\)
      \(\frac{1}{3}x\geq 2\)   \(−2x\geq −2\)
      \(x\geq 6\) na \(x\leq 1\)
    Grafu kila suluhisho. ...
    Grafu namba
    zinazofanya kutofautiana kwa
    kweli.    		 ...
      Hakuna namba zinazofanya kutofautiana kwa wote kuwa kweli.

    Hii ni utata kwa hiyo hakuna suluhisho. Hakuna namba zinazofanya kutofautiana kwa kweli.

    Hii ni utata kwa hiyo hakuna suluhisho. Hakuna namba zinazofanya kutofautiana kwa kweli.

    Hii ni utata kwa hiyo hakuna suluhisho.
    Mfano\(\PageIndex{8}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(\frac{1}{4}x−3\geq −1\) na\(−3(x−2)\geq 2\).

    Jibu

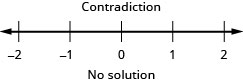
    Ukosefu wa usawa ni utata. Kwa hiyo, hakuna suluhisho. Matokeo yake, hakuna grafu ya mstari wa nambari au notation ya muda.

    Mfano\(\PageIndex{9}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(\frac{1}{5}x−5\geq −3\) na\(−4(x−1)\geq −2\).

    Jibu

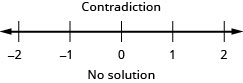
    Ukosefu wa usawa ni utata. Kwa hiyo, hakuna suluhisho. Matokeo yake, hakuna grafu au mstari wa nambari au notation ya muda.

    Wakati mwingine tuna usawa wa kiwanja ambao unaweza kuandikwa kwa ufupi zaidi. Kwa mfano,\(a<x\) na\(x<b\) inaweza kuandikwa tu kama\(a<x<b\) na kisha tunaiita usawa mara mbili. Aina mbili ni sawa.

    USAWA MARA MBILI

    Ukosefu wa usawa mara mbili ni usawa wa kiwanja kama vile\(a<x<b\). Ni sawa na\(a<x\) na\(x<b\).

    \[\text{Other forms:} \quad \begin{array} {lllll} {a<x<b} &{\text{is equivalent to }} &{a<x} &{\text{and}} &{x<b} \\ {a\leq x\leq b} &{\text{is equivalent to }} &{a\leq x} &{\text{and}} &{x\leq b} \\ {a>x>b} &{\text{is equivalent to }} &{a>x} &{\text{and}} &{x>b} \\ {a\geq x\geq b} &{\text{is equivalent to }} &{a\geq x} &{\text{and}} &{x\geq b} \\ \end{array} \nonumber\]

    Ili kutatua usawa mara mbili tunafanya operesheni sawa kwenye “sehemu” zote tatu za usawa mara mbili kwa lengo la kutenganisha kutofautiana katikati.

    Mfano\(\PageIndex{10}\)

    Kutatua\(−4\leq 3x−7<8\). Grafu suluhisho na uandike suluhisho katika maelezo ya muda.

    Jibu
      \(-4 \leq 3x - 7 < 8\)
    Ongeza 7 hadi sehemu zote tatu. \( -4 \,{\color{red}{+\, 7}} \leq 3x - 7 \,{\color{red}{+ \,7}} < 8 \,{\color{red}{+ \,7}}\)
    Kurahisisha. \( 3 \le 3x < 15 \)
    Gawanya kila sehemu kwa tatu. \( \dfrac{3}{\color{red}{3}} \leq \dfrac{3x}{\color{red}{3}} < \dfrac{15}{\color{red}{3}} \)
    Kurahisisha. \( 1 \leq x < 5 \)
    Graph suluhisho. .
    Andika suluhisho katika maelezo ya muda. \( [1, 5) \)

    Wakati imeandikwa kama kukosekana kwa usawa mara mbili\(1\leq x<5\),, ni rahisi kuona kwamba ufumbuzi ni idadi hawakupata kati ya moja na tano, ikiwa ni pamoja na moja, lakini si tano. Tunaweza kisha grafu suluhisho mara moja kama tulivyofanya hapo juu.

    Njia nyingine ya grafu ufumbuzi wa\(1\leq x<5\) ni graph wote ufumbuzi wa\(x\geq 1\) na ufumbuzi wa\(x<5\). Tungependa kisha kupata idadi kwamba kufanya wote usawa kweli kama tulivyofanya katika mifano ya awali.

    Mfano\(\PageIndex{11}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(−5\leq 4x−1<7\).

    Jibu

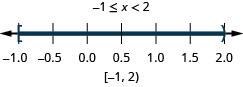
    Suluhisho ni hasi 1 ni chini ya au sawa na x ambayo ni chini ya 2. Grafu yake ina mduara uliofungwa kwenye hasi 1 na mduara wazi saa 2 na kivuli kati ya miduara iliyofungwa na ya wazi. Uthibitishaji wake wa muda ni hasi 1 hadi 2 ndani ya bracket na mabano.

    Mfano\(\PageIndex{12}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(−3<2x−5\leq 1\).

    Jibu

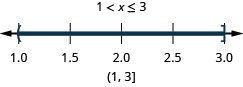
    ufumbuzi ni 1 ni chini ya x ambayo ni chini ya au sawa na 3. Grafu yake ina mduara wazi saa 1 na mduara uliofungwa saa 3 na kivuli kati ya miduara iliyofungwa na ya wazi. Uthibitishaji wake wa muda ni hasi 1 hadi 3 ndani ya mabano na bracket.

    Tatua Usawa wa Kiwanja na “au”

    Ili kutatua usawa wa kiwanja na “au”, tunaanza tu kama tulivyofanya na kutofautiana kwa kiwanja na “na” - sisi kutatua kutofautiana mbili. Kisha sisi kupata namba zote kwamba kufanya ama kukosekana kwa usawa kweli.

    Kama vile Marekani ni muungano wa majimbo yote 50, suluhisho litakuwa muungano wa namba zote zinazofanya usawa wa kweli. Ili kupata suluhisho la usawa wa kiwanja, tunaangalia grafu za kila usawa, tafuta namba ambazo ni za grafu na kuweka namba hizo zote pamoja.

    Kuandika ufumbuzi katika notation ya muda, sisi mara nyingi kutumia ishara ya muungano\(\cup\), kuonyesha muungano wa ufumbuzi inavyoonekana katika grafu.

    KUTATUA USAWA KIWANJA NA “AU.”
    1. Kutatua kila usawa.
    2. Grafu kila suluhisho. Kisha graph idadi kwamba kufanya ama usawa kweli.
    3. Andika suluhisho katika maelezo ya muda.
    Mfano\(\PageIndex{13}\)

    Kutatua\(5−3x\leq −1\) au\(8+2x\leq 5\). Grafu suluhisho na uandike suluhisho katika maelezo ya muda.

    Jibu
      \(5−3x\leq −1\) au \(8+2x\leq 5\)
    Kutatua kila usawa. \(5−3x\leq −1\)   \(8+2x\leq 5\)
      \(−3x\leq −6\)   \(2x\leq −3\)
      \(x\geq 2\) au \(x\leq −\frac{3}{2}\)
    Grafu kila suluhisho. .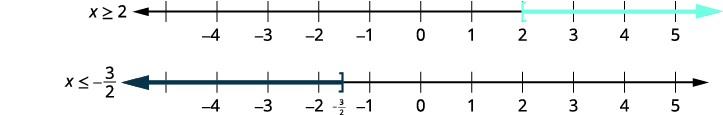
    Nambari za grafu ambazo
    hufanya usawa wa
    kweli.    		 .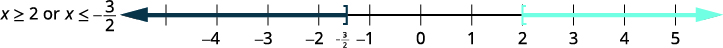
      \((−\infty,−32]\cup[2,\infty)\)
    Mfano\(\PageIndex{14}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(1−2x\leq −3\) au\(7+3x\leq 4\).

    Jibu

    Suluhisho ni x ni kubwa kuliko au sawa na 2 au x ni chini ya au sawa na 1. Grafu ya ufumbuzi kwenye mstari wa nambari ina mduara uliofungwa kwenye hasi 1 na kivuli upande wa kushoto na mduara uliofungwa saa 2 na shading kwa haki. Muda nukuu ni muungano wa infinity hasi kwa hasi 1 ndani ya mabano na bracket na 2 na infinity ndani ya bracket na mabano.

    Mfano\(\PageIndex{15}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(2−5x\leq −3\) au\(5+2x\leq 3\).

    Jibu

    Suluhisho ni x ni kubwa kuliko au sawa na 1 au x ni chini ya au sawa na hasi 1. Grafu ya ufumbuzi kwenye mstari wa nambari ina mduara uliofungwa kwenye hasi 1 na kivuli upande wa kushoto na mduara uliofungwa saa 1 na shading kwa haki. Muda nukuu ni muungano wa infinity hasi kwa hasi 1 ndani ya mabano na bracket na 1 na infinity ndani ya bracket na mabano.

    Mfano\(\PageIndex{16}\)

    Kutatua\(\frac{2}{3}x−4\leq 3\) au\(\frac{1}{4}(x+8)\geq −1\). Grafu suluhisho na uandike suluhisho katika maelezo ya muda.

    Jibu
      \(\frac{2}{3}x−4\leq 3\) au \(\frac{1}{4}(x+8)\geq −1\)
    Kutatua kila
    kukosekana kwa usawa.    		 \(3(\frac{2}{3}x−4)\leq 3(3)\)   \(4⋅\frac{1}{4}(x+8)\geq 4⋅(−1)\)
      \(2x−12\leq 9\)   \(x+8\geq −4\)
      \(2x\leq 21\)   \(x\geq −12\)
      \(x\leq \frac{21}{2}\)    
      \(x\leq \frac{21}{2}\) au \(x\geq −12\)
    Grafu kila
    suluhisho.    		 .
    Nambari za grafu
    ambazo hufanya
    usawa wa kweli.    		 .
      Suluhisho linashughulikia namba zote halisi.
      \((−\infty ,\infty )\)
    Mfano\(\PageIndex{17}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(\frac{3}{5}x−7\leq −1\) au\(\frac{1}{3}(x+6)\geq −2\).

    Jibu

    Suluhisho ni utambulisho. Suluhisho lake kwenye mstari wa nambari ni kivuli kwa maadili yote. Suluhisho katika notation ya muda ni infinity hasi kwa infinity ndani ya mabano.

    Mfano\(\PageIndex{18}\)

    Tatua usawa wa kiwanja. Grafu suluhisho na uandike suluhisho katika maelezo ya muda:\(\frac{3}{4}x−3\leq 3\) au\(\frac{2}{5}(x+10)\geq 0\).

    Jibu

    Suluhisho ni utambulisho. Suluhisho lake kwenye mstari wa nambari ni kivuli kwa maadili yote. Suluhisho katika notation ya muda ni infinity hasi kwa infinity ndani ya mabano.

    Tatua Maombi na Usawa wa Kiwanja

    Hali katika ulimwengu wa kweli pia huhusisha kutofautiana kwa kiwanja. Tutatumia huo kutatua tatizo mkakati kwamba sisi kutumika kutatua linear equation na maombi usawa.

    Kumbuka mikakati ya kutatua tatizo ni ya kwanza kusoma tatizo na kuhakikisha maneno yote yanaeleweka. Kisha, kutambua nini sisi ni kuangalia kwa na kuwapa variable kuwakilisha ni. Ifuatayo, rejesha tatizo katika sentensi moja ili iwe rahisi kutafsiri katika usawa wa kiwanja. Mwisho, sisi kutatua usawa kiwanja.

    Mfano\(\PageIndex{19}\)

    Kutokana na ukame huko California, jamii nyingi zina viwango vya maji vya tiered. Kuna viwango tofauti vya Matumizi ya Uhifadhi, Matumizi ya kawaida na Matumizi makubwa. Matumizi hupimwa kwa idadi ya miguu mia za ujazo (hcf) mmiliki wa mali anatumia.

    Wakati wa majira ya joto, mmiliki wa mali atalipa $24.72 pamoja na $1.54 kwa hcf kwa Matumizi ya kawaida. Muswada wa Matumizi ya kawaida utakuwa kati au sawa na $57.06 na $171.02. Ni hcf ngapi anayeweza kutumia mmiliki ikiwa anataka matumizi yake kukaa katika aina ya kawaida?

    Jibu
    Tambua kile tunachotafuta. Idadi ya hcf anaweza kutumia na kukaa katika “matumizi ya kawaida” bili mbalimbali.
    Jina kile tunachotafuta. Hebu x=x= idadi ya hcf anaweza kutumia.
    Tafsiri kwa usawa. Bill ni $24.72 pamoja $1.54 mara idadi ya HCF anatumia au\(24.72+1.54x\).
     

    \(\color{Cerulean}{\underbrace{\color{black}{\text{His bill will be between or equal to }$57.06\text{ and }$171.02.}}}\)

    \(57.06 \leq 24.74 + 1.54x \leq 171.02 \)
    Kutatua kukosekana kwa usawa.

    \(57.06 \leq 24.74 + 1.54x \leq 171.02\)

    \(57.06 \,{\color{red}{- \,24.72}}\leq 24.74 \,{\color{red}{- \,24.72}} + 1.54x \leq 171.02 \,{\color{red}{- \,24.72}}\)

    \( 32.34 \leq 1.54x \leq 146.3\)

    \( \dfrac{32.34}{\color{red}{1.54}} \leq \dfrac{1.54x}{\color{red}{1.54}} \leq \dfrac{146.3}{\color{red}{1.54}}\)

    \( 21 \leq x \leq 95 \)
    Jibu swali. Mmiliki wa mali anaweza kutumia\(21–95\) hcf na bado huanguka ndani ya “matumizi ya kawaida” ya bili.
    Mfano\(\PageIndex{20}\)

    Kutokana na ukame huko California, jamii nyingi sasa zina viwango vya maji vya tiered. Kuna viwango tofauti vya Matumizi ya Uhifadhi, Matumizi ya kawaida na Matumizi makubwa. Matumizi hupimwa kwa idadi ya miguu mia za ujazo (hcf) mmiliki wa mali anatumia.

    Wakati wa majira ya joto, mmiliki wa mali atalipa $24.72 pamoja na $1.32 kwa hcf kwa Matumizi ya Uhifadhi. Muswada wa Matumizi ya Uhifadhi utakuwa kati au sawa na $31.32 na $52.12. Ni hcf ngapi anayeweza kutumia mmiliki ikiwa anataka matumizi yake kukaa katika aina ya uhifadhi?

    Jibu

    Mmiliki wa nyumba anaweza kutumia\(5–20\) hcf na bado huanguka ndani ya “matumizi ya uhifadhi” wa bili.

    Mfano\(\PageIndex{21}\)

    Kutokana na ukame huko California, jamii nyingi zina viwango vya maji vya tiered. Kuna viwango tofauti vya Matumizi ya Uhifadhi, Matumizi ya kawaida na Matumizi makubwa. Matumizi hupimwa kwa idadi ya miguu mia za ujazo (hcf) mmiliki wa mali anatumia.

    Wakati wa majira ya baridi, mmiliki wa mali atalipa $24.72 pamoja na $1.54 kwa hcf kwa Matumizi ya kawaida. Muswada wa Matumizi ya kawaida utakuwa kati au sawa na $49.36 na $86.32. Ni ngapi hcf ataruhusiwa kutumia kama anataka matumizi yake kukaa katika aina ya kawaida?

    Jibu

    Mmiliki wa nyumba anaweza kutumia\(16–40\) hcf na bado huanguka ndani ya “matumizi ya kawaida” ya bili.

    Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na kutatua usawa wa kiwanja.

    • Kiwanja usawa

    Dhana muhimu

    • Jinsi ya kutatua usawa wa kiwanja na “na”
      1. Kutatua kila usawa.
      2. Grafu kila suluhisho. Kisha grafu namba zinazofanya kutofautiana kwa kweli. Grafu hii inaonyesha suluhisho la usawa wa kiwanja.
      3. Andika suluhisho katika maelezo ya muda.
    • Mara mbili kukosekana usawa
      • Ukosefu wa usawa mara mbili ni usawa wa kiwanja kama vile\(a<x<b\). Ni sawa\(a<x\) na na aina\(x<b.\)

        nyingine:\ [kuanza {align*} a<x<b & &\ maandishi {ni sawa na} & a<x\;\ maandishi {na}\; x<b\\
        a≤ x≤ b & &\ maandishi {ni sawa na} & a≤ x\;\ maandishi {na}\; x≤ b\ \
        a>x>b & &\ maandishi {ni sawa na} & a>x\;\ maandishi {na}\; x>b\\
        a≥ x≥ b & &\ maandishi {ni sawa na} & & a≥ x\;\ maandishi {na}\; x≥ b\ mwisho {align*}\]
    • Jinsi ya kutatua usawa wa kiwanja na “au”
      1. Kutatua kila usawa.
      2. Grafu kila suluhisho. Kisha graph idadi kwamba kufanya ama usawa kweli.
      3. Andika suluhisho katika maelezo ya muda.

    faharasa

    usawa wa kiwanja
    Ukosefu wa usawa wa kiwanja unajumuisha kutofautiana mbili zinazounganishwa na neno “na” au neno “au.”