2.6: Kutatua Usawa wa Linear

Last updated

Nov 1, 2022
Page ID
176733
Save as PDF
- 2.5E: Mazoezi
- 2.6E: Mazoezi

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Usawa wa Grafu kwenye mstari wa nambari
Kutatua usawa linear
Tafsiri maneno kwa usawa na kutatua
Tatua programu na kutofautiana kwa mstari

Kabla ya kuanza, fanya jaribio hili la utayari.

Tafsiri kutoka algebra hadi Kiingereza: $15>x$ .
Ikiwa umekosa tatizo hili, tathmini [kiungo].
Tafsiri kwa kujieleza algebraic: $15$ ni chini ya $x$ .
Ikiwa umekosa tatizo hili, tathmini [kiungo].

Usawa wa Grafu kwenye Mstari wa Idadi

Nambari gani ingeweza kufanya usawa $x>3$ kuwa kweli? Je, unafikiri, " $x$ inaweza kuwa nne”? Hiyo ni sahihi, lakini $x$ inaweza kuwa 6, pia, au 37, au hata 3.001. Nambari yoyote kubwa kuliko tatu ni suluhisho la kutofautiana $x>3$ . Tunaonyesha ufumbuzi wote wa kutofautiana $x>3$ kwenye mstari wa namba kwa kuzingatia namba zote kwa haki ya tatu, kuonyesha kwamba namba zote kubwa kuliko tatu ni ufumbuzi. Kwa sababu namba tatu yenyewe sio suluhisho, tunaweka mabano ya wazi kwa tatu.

Tunaweza pia kuwakilisha usawa kwa kutumia muda nukuu. Hakuna mwisho juu ya ufumbuzi wa usawa huu. Katika nukuu ya muda, tunaelezea $x>3$ kama $(3,\infty)$ . Ishara $\infty$ inasomewa kama “infinity.” Si idadi halisi. Kielelezo $\PageIndex{1}$ kinaonyesha mstari wa nambari na notation ya muda.

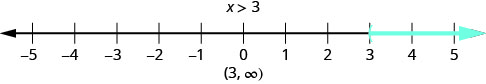
Takwimu inaonyesha kutofautiana, x ni kubwa kuliko 3, iliyowekwa kwenye mstari wa nambari kutoka hasi 5 hadi 5. Kuna shading inayoanza saa 3 na inaendelea kwa idadi kwa haki yake. Suluhisho la kukosekana kwa usawa limeandikwa katika maelezo ya muda. Ni muda kutoka 3 hadi infinity, si ikiwa ni pamoja na 3. — Kielelezo $\PageIndex{1}$ : Ukosefu wa usawa $x>3$ umewekwa kwenye mstari huu wa nambari na imeandikwa katika nukuu ya muda.

Tunatumia alama ya mabano ya kushoto, (, ili kuonyesha kwamba mwisho wa usawa haujajumuishwa. kushoto mabano ishara, [, inaonyesha kwamba endpoint ni pamoja na.

Ukosefu wa usawa $x\leq 1$ unamaanisha namba zote chini au sawa na moja. Hapa tunahitaji kuonyesha kwamba moja ni suluhisho, pia. Sisi kufanya hivyo kwa kuweka mabano katika $x=1$ . Sisi kisha kivuli katika namba zote upande wa kushoto wa moja, ili kuonyesha kwamba namba zote chini ya moja ni ufumbuzi (Kielelezo $\PageIndex{2}$ ). Hakuna mwisho chini ya idadi hizo. Tunaandika $x\leq 1x\leq 1$ katika nukuu ya muda kama $(−\infty,1]$ . Ishara $−\infty$ inasomewa kama “infinity hasi.”

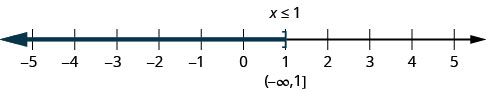
Takwimu inaonyesha kutofautiana, x ni chini ya au sawa na l, iliyowekwa kwenye mstari wa nambari kutoka hasi 5 hadi 5. Kuna kivuli kinachoanza saa 1 na kinaendelea kwa namba upande wa kushoto. Suluhisho la kukosekana kwa usawa limeandikwa katika maelezo ya muda. Ni muda kutoka infinity hasi kwa moja, Ikiwa ni pamoja na 1. — Kielelezo $\PageIndex{2}$ : Ukosefu wa usawa $x\leq 1$ umewekwa kwenye mstari huu wa nambari na imeandikwa katika nukuu ya muda.

Kielelezo $\PageIndex{3}$ kinaonyesha mstari wa nambari na notation ya muda.

USAWA, MISTARI YA NAMBA, NA NOTATION YA MUDA

$Takwimu inaonyesha kwamba ufumbuzi wa usawa x ni mkubwa kuliko unahitajika kwenye mstari wa namba na mabano ya kushoto kwenye na kivuli kwa haki, na kwamba suluhisho katika nukuu ya muda ni muda kutoka kwa infinity iliyoambatanishwa katika mabano. Inaonyesha ufumbuzi wa kukosekana kwa usawa x ni kubwa kuliko au sawa na unahitajika kwenye mstari namba na mabano kushoto katika na shading na haki, na kwamba ufumbuzi katika muda nukuu ni muda a kwa infinity ndani ya mabano kushoto na mabano haki. Inaonyesha kwamba ufumbuzi wa kukosekana kwa usawa x ni chini ya unahitajika kwenye mstari namba na mabano haki katika na shading upande wa kushoto, na kwamba ufumbuzi katika muda nukuu ni muda infinity hasi kwa ndani ya mabano. Inaonyesha kwamba ufumbuzi wa kukosekana kwa usawa x ni chini ya au sawa na unahitajika kwenye mstari number na mabano haki katika na shading upande wa kushoto, na kwamba ufumbuzi katika muda nukuu ni hasi infinity ndani ya mabano kushoto na mabano haki.$

Nukuu ya kutofautiana kwenye mstari wa nambari na katika nukuu ya muda hutumia alama sawa ili kuelezea mwisho wa vipindi.

Mfano $\PageIndex{1}$

Grafu kila usawa kwenye mstari wa nambari na uandike katika nukuu ya muda.

$x\geq −3$
$x<2.5$
$x\leq −\frac{3}{5}$

Jibu

ⓐ

	$x \geq -3$
Kivuli na haki ya $−3$ , na kuweka mabano katika $−3$ .	$.$
Andika katika notation ya muda.	$[-3, \infty)$

ⓑ

	$x < 2.5$
Shade upande wa kushoto wa 2.5 na kuweka mabano saa 2.5.	$.$
Andika katika notation ya muda.	$(-\infty, 2.5)$

ⓒ

	$x \leq -\dfrac{3}{5}$
Kivuli upande wa kushoto wa $−\frac{3}{5}$ , na kuweka mabano katika $−\frac{3}{5}$ .	$.$
Andika katika notation ya muda.	$\bigg( -\infty, \dfrac{3}{5}\bigg]$

Grafu kila usawa kwenye mstari wa nambari na uandike kwa nukuu ya muda:

$x>2$
$x\leq −1.5$
$x\geq \frac{3}{4}$ .

Jibu

ⓐ

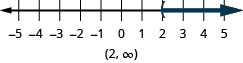
$Grafu ya usawa x ni kubwa kuliko 2 inavyoonyeshwa kwenye mstari wa nambari na mabano ya kushoto saa 2 na kushona kwa haki. Suluhisho katika notation ya muda ni muda kutoka 2 hadi infinity iliyofungwa ndani ya mabano.$

ⓑ

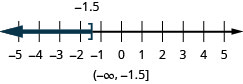
$Grafu ya usawa x ni chini ya au sawa na 1.5 hasi inavyoonyeshwa kwenye mstari wa namba na bracket sahihi katika hasi 1.5 na shading upande wa kushoto. Suluhisho katika maelezo ya muda ni muda kutoka kwa infinity hasi hadi hasi 1.5 iliyofungwa ndani ya mabano ya kushoto na bracket ya kulia.$

ⓒ

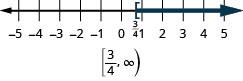
$Grafu ya usawa x ni kubwa kuliko au sawa na nne tatu inavyoonyeshwa kwenye mstari wa nambari na bracket ya kushoto saa tatu na shading kwa haki. Suluhisho katika maelezo ya muda ni muda kutoka kwa nne tatu hadi infinity iliyofungwa ndani ya bracket ya kushoto na mabano ya kushoto.$

Mfano $\PageIndex{3}$

Grafu kila usawa kwenye mstari wa nambari na uandike kwa nukuu ya muda:

$x\leq −4$
$x\geq 0.5$
$x<−\frac{2}{3}$ .

Jibu

ⓐ

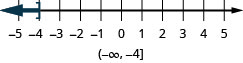
$Grafu ya usawa x ni chini ya au sawa na hasi 4 inavyoonyeshwa kwenye mstari wa namba na bracket sahihi katika hasi 4 na shading upande wa kushoto. Suluhisho katika maelezo ya muda ni muda kutoka kwa infinity hasi hadi hasi 4 iliyofungwa ndani ya mabano ya kushoto na bracket ya kulia.$

ⓑ

$Grafu ya usawa x ni kubwa kuliko au sawa na 0.5 inavyoonyeshwa kwenye mstari wa namba na bracket ya kushoto saa 0.5 na kivuli kwa haki. Suluhisho katika maelezo ya muda ni muda kutoka 0.5 hadi infinity iliyofungwa ndani ya bracket ya kushoto na mabano ya kulia.$

ⓒ

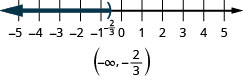
$Grafu ya usawa x ni chini ya theluthi mbili hasi inavyoonyeshwa kwenye mstari wa namba na mabano sahihi kwa theluthi mbili hasi na kivuli upande wa kushoto. Suluhisho katika maelezo ya muda ni muda kutoka kwa infinity hasi hadi theluthi mbili hasi iliyofungwa ndani ya mabano.$

Nambari gani ni kubwa kuliko mbili lakini chini ya tano? Je, unafikiri kusema, $2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99$ ? Tunaweza kuwakilisha namba zote kati ya mbili na tano na usawa $2<x<5$ . Tunaweza kuonyesha $2<x<5$ kwenye mstari wa nambari kwa kufungia namba zote kati ya mbili na tano. Tena, tunatumia mabano kuonyesha namba mbili na tano hazijumuishwa. Angalia Kielelezo.

Grafu ya usawa 2 ni chini ya x ambayo ni chini ya 5 inaonyesha duru wazi 2 na 5 na shading katikati. — Kielelezo $\PageIndex{3}$

Grafu kila usawa kwenye mstari wa nambari na uandike katika nukuu ya muda.

ⓐ $−3<x<4$ ⓑ $−6\leq x<−1$ ⓒ $0\leq x\leq 2.5$

Jibu

ⓐ

		$-3 < x < 4$
Kivuli kati $−3$ na 4. Weka mabano katika $−3$ na 4.		$.$
Andika katika notation ya muda.		$(-3,4)$

ⓑ

			$-6 \leq x < -1$
Kivuli kati $−6$ na -1. Weka bracket saa $−6$ , na mabano katika -1.			$.$
Andika katika notation ya muda.			$[-6,1)$

ⓒ

			$0 \leq x \leq 2.5$
Kivuli kati ya 0 na 2.5. Weka bracket saa 0 na saa 2.5.			$.$
Andika katika notation ya muda.			$[0, 2.5]$

Mfano $\PageIndex{5}$

Grafu kila usawa kwenye mstari wa nambari na uandike kwa nukuu ya muda:

ⓐ $−2<x<1$ ⓑ $−5\leq x<−4$ ⓒ $1\leq x\leq 4.25$

Jibu

ⓐ

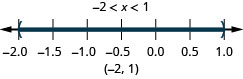
$hasi 2 ni chini x ambayo ni chini ya 1. Kuna miduara ya wazi katika hasi 2 na 1 na kivuli kati ya hasi 2 na 1 kwenye mstari wa namba. Weka mabano kwa hasi 2 na 1. Andika katika notation ya muda.$

ⓑ

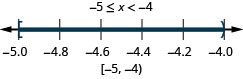
$Hasi 5 ni chini ya au sawa na x ambayo ni chini ya hasi 4. Kuna mduara uliofungwa kwenye hasi 6 na mduara wazi kwenye hasi 4 na kivuli kati ya hasi 5 na hasi 4 kwenye mstari wa namba. Weka bracket katika hasi 5 na mabano katika hasi 4. Andika katika notation ya muda.$

ⓒ

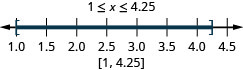
$1 ni chini ya au sawa na x ambayo ni chini ya 4.25. Kuna mduara uliofungwa saa 1 na mduara uliofungwa saa 4.25 na kivuli kati ya 1 na 4.25 kwenye mstari wa namba. Weka mabano saa 1 na 4.25. Andika katika notation ya muda.$

Mfano $\PageIndex{6}$

Grafu kila usawa kwenye mstari wa nambari na uandike kwa nukuu ya muda:

ⓐ $−6<x<2$ ⓑ $−3\leq x< −1$ ⓒ $2.5\leq x\leq 6$

Jibu

ⓐ

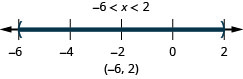
$hasi 6 ni chini ya x ambayo ni chini ya 2. Kuna mduara wazi katika hasi 6 na mduara wazi saa 2 na kivuli kati ya hasi 6 na 2 kwenye mstari wa nambari. Weka mabano kwa hasi 6 na 2. Andika katika notation ya muda.$

ⓑ

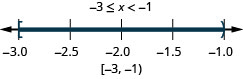
$Hasi 3 ni chini ya au sawa na x ambayo ni chini ya hasi 1. Kuna mduara uliofungwa kwenye hasi 3 na mduara wazi kwenye hasi 1 na kivuli kati ya hasi 3 na hasi 1 kwenye mstari wa namba. Weka bracket katika hasi 3 na mabano katika hasi 1. Andika katika notation ya muda.$

ⓒ

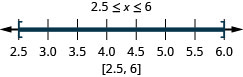
$2.5 ni chini ya au sawa na x ambayo ni chini ya au sawa na 6. Kuna mduara uliofungwa saa 2.5 na mduara uliofungwa saa 6 na kivuli kati ya 2.5 na 6 kwenye mstari wa namba. Weka mabano saa 2.5 na 6. Andika katika notation ya muda.$

Kutatua Usawa Linear

Ukosefu wa usawa wa mstari ni sawa na usawa wa linear—lakini ishara sawa inabadilishwa na ishara ya usawa. Ukosefu wa usawa wa mstari ni usawa katika kutofautiana moja ambayo inaweza kuandikwa katika moja ya fomu $ax+b<c$ , $ax+b\leq c$ , $ax+b>c$ , au $ax+b\geq c$ .

USAWA WA MSTARI

Ukosefu wa usawa wa mstari ni usawa katika variable moja ambayo inaweza kuandikwa katika mojawapo ya fomu zifuatazo ambapo $a, \, b,$ na $c$ ni namba halisi na $a≠0$ :

$\begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}$

Tulipotatua equations linear, tuliweza kutumia mali ya usawa kuongeza, kuondoa, kuzidisha, au kugawanya pande zote mbili na bado kuweka usawa. Sawa mali kushikilia kweli kwa kukosekana kwa usawa.

Tunaweza kuongeza au kuondoa kiasi sawa kutoka pande zote mbili za usawa na bado kuweka usawa. Kwa mfano:

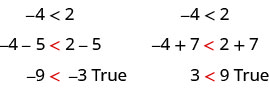
$Hasi 4 ni chini ya 2. Hasi 4 minus 5 ni chini ya 2 minus 5. Hasi 9 ni chini ya hasi 3, ambayo ni kweli. Hasi 4 ni chini ya 2. Hasi 4 pamoja na 7 ni chini ya 2 pamoja na 7. 3 ni chini ya 9, ambayo ni kweli.$

Angalia kwamba ishara ya kukosekana kwa usawa ilikaa sawa.

Hii inatuongoza kwenye Mali ya Kuongeza na Kuondoa ya Usawa.

KUONGEZA NA KUTOA MALI YA KUTOFAUTIANA

Kwa idadi yoyote $a, \, b,$ na $c,$ kama $a<b$ , basi

$\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}$

Tunaweza kuongeza au kuondoa kiasi sawa kutoka pande zote mbili za usawa na bado kuweka usawa

Ni nini kinachotokea kwa kukosekana kwa usawa tunapogawanya au kuzidisha pande zote mbili kwa mara?

Hebu kwanza tuongeze na kugawanya pande zote mbili kwa idadi nzuri.

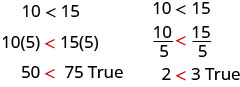
$10 ni chini ya 15. Mara 10 ni chini ya mara 15 5. 50 ni chini ya 75 ni kweli. 10 ni chini ya 15. 10 imegawanywa na 5 ni chini ya 15 imegawanywa na 5. 2 ni chini ya 3 ni kweli.$

Ishara za kutofautiana zilikaa sawa.

Je, usawa hukaa sawa wakati tunapogawanya au kuzidisha kwa idadi hasi?

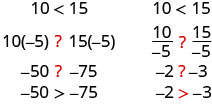
$10 ni chini ya 15 mara 10 hasi 5 ni tupu mara 15 hasi 5? Hasi 50 ni tupu hasi 75. Hasi 50 ni kubwa kuliko hasi 75. 10 ni chini ya 15. 10 imegawanywa na hasi 5 ni tupu 15 imegawanywa na hasi 5. Hasi 2 ni tupu hasi 3. Hasi 2 ni tupu hasi 3.$

Angalia kwamba tulipojaza ishara za kutofautiana, ishara za kutofautiana zilibadilisha mwelekeo wao.

Tunapogawanya au kuzidisha usawa kwa idadi nzuri, ishara ya usawa inabakia sawa. Tunapogawanya au kuzidisha usawa kwa idadi hasi, ishara ya usawa inarudi.

Hii inatupa Kuzidisha na Idara ya Mali ya Ukosefu wa usawa.

KUZIDISHA NA MGAWANYIKO MALI YA USAWA

Kwa idadi yoyote $a, \, b,$ na $c,$

$\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}$

Tunapogawanya au kuzidisha usawa kwa $a$ :

idadi chanya, kukosekana kwa usawa anakaa sawa.
idadi hasi, kukosekana kwa usawa reverses.

Wakati mwingine wakati wa kutatua usawa, kama katika mfano unaofuata, kutofautiana huisha juu ya haki. Tunaweza kuandika upya kukosekana kwa usawa katika reverse kupata variable kwa upande wa kushoto.

$x>a \text{ has the same meaning as } a<x \nonumber$

Fikiria juu yake kama “Ikiwa Xander ni mrefu kuliko Andy, basi Andy ni mfupi kuliko Xander.”

Mfano $\PageIndex{7}$

Kutatua kila usawa. Grafu suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

ⓐ $x−\frac{3}{8}\leq \frac{3}{4}$ ⓑ $9y<54$ ⓒ $−15<\frac{3}{5}z$

Jibu

ⓐ

	$.$
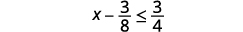
Ongeza 3838 kwa pande zote mbili za usawa.	$.$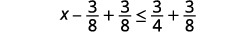
Kurahisisha.	$.$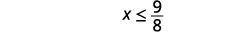
Grafu suluhisho kwenye mstari wa nambari.	$.$
Andika suluhisho katika maelezo ya muda.	$.$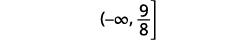

ⓑ

	$.$
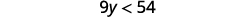
Gawanya pande zote mbili za usawa na 9; tangu 9 ni chanya, usawa unakaa sawa.	$.$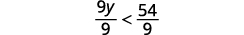
Kurahisisha.	$.$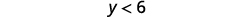
Grafu suluhisho kwenye mstari wa nambari.	$.$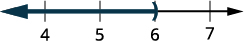
Andika suluhisho katika maelezo ya muda.	$.$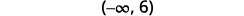

ⓒ

	$.$
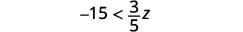
Kuzidisha pande zote mbili za kukosekana kwa usawa na $\frac{5}{3}$ . Kwa kuwa $\frac{5}{3}$ ni chanya, ukosefu wa usawa unakaa sawa.	$.$
Kurahisisha.	$.$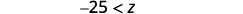
Andika upya na kutofautiana upande wa kushoto.	$.$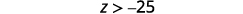
Grafu suluhisho kwenye mstari wa nambari.	$.$
Andika suluhisho katika maelezo ya muda.	$.$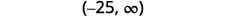

Tatua kila usawa, graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda:

ⓐ $p−\frac{3}{4}\geq \frac{1}{6}$ ⓑ $9c>72$ ⓒ $24\leq \frac{3}{8}m$

Jibu

ⓐ

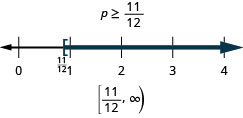
$p ni chini ya kumi na moja na kumi na mbili. Suluhisho kwenye mstari wa nambari ina bracket sahihi katika kumi na moja na kumi na mbili na shading kwa haki. Suluhisho katika maelezo ya muda ni, kumi na moja na kumi na mbili hadi infinity ndani ya bracket na mabano.$

ⓑ

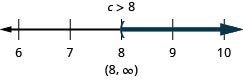
$c ni chini ya 8. Suluhisho kwenye mstari wa nambari ina bracket ya kushoto saa 8 na shading kwa haki. Suluhisho katika maelezo ya muda ni, 8 hadi infinity ndani ya mabano.$

ⓒ

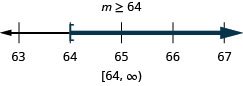
$m ni kubwa kuliko au sawa na 8. Suluhisho kwenye mstari wa nambari ina bracket sahihi saa 64 na shading kwa haki. ufumbuzi katika nukuu ya muda ni, 64 kwa infinity ndani ya bracket na mabano.$

Mfano $\PageIndex{9}$

Tatua kila usawa, graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda:

ⓐ $r−\frac{1}{3}\leq \frac{7}{12}$ ⓑ $12d\leq 60$ ⓒ $−24<\frac{4}{3}n$

Jibu

ⓐ

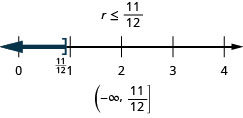
$r ni chini ya au sawa na kumi na moja na kumi na mbili. Suluhisho kwenye mstari wa nambari ina bracket ya kushoto saa kumi na moja na kumi na mbili na shading upande wa kushoto. Suluhisho katika maelezo ya muda ni infinity hasi kwa kumi na moja na kumi na mbili ndani ya mabano na bracket.$

ⓑ

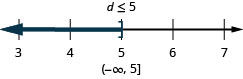
$c ni chini ya au sawa na 5. Suluhisho kwenye mstari wa nambari ina bracket sahihi saa 5 na shading upande wa kushoto. Suluhisho katika notation ya muda ni infinity hasi kwa 5 ndani ya mabano na bracket.$

ⓒ

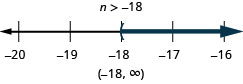
$n ni kubwa kuliko hasi 18. Suluhisho kwenye mstari wa nambari ina mabano ya kushoto katika hasi 18 na shading kwa haki. Suluhisho katika notation ya muda ni hasi 18 hadi infinity ndani ya mabano.$

Kuwa makini wakati unapozidisha au ugawanye na nambari hasi - kumbuka kubadili ishara ya usawa.

Mfano $\PageIndex{10}$

Tatua kila usawa, graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

ⓐ $−\frac{1}{3}m\geq \frac{6}{5}$ ⓑ $\frac{n}{−2} \geq 8$

Jibu

ⓐ

	$.$
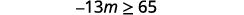
Gawanya pande zote mbili za usawa na $−\frac{1}{3}$ . Kwa kuwa $−\frac{1}{3}$ ni hasi, ukosefu wa usawa unarudi.	$.$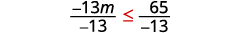
Kurahisisha.	$.$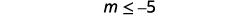
Grafu suluhisho kwenye mstari wa nambari.	$.$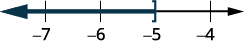
Andika suluhisho katika maelezo ya muda.	$.$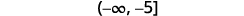

ⓑ

	$.$
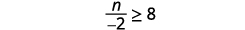
Kuzidisha pande zote mbili za kukosekana kwa usawa na $−2$ . Kwa kuwa $−2$ ni hasi, ukosefu wa usawa unarudi.	$.$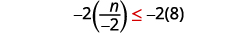
Kurahisisha.	$.$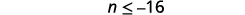
Grafu suluhisho kwenye mstari wa nambari.	$.$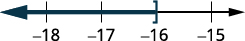
Andika suluhisho katika maelezo ya muda.	$.$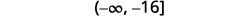

Mfano $\PageIndex{11}$

Tatua kila usawa, graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda:

ⓐ $−8q<32$ ⓑ $\frac{k}{−12} \leq 15$ .

Jibu

ⓐ

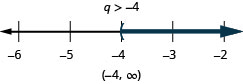
$q ni kubwa kuliko au sawa na hasi 4. Suluhisho kwenye mstari wa nambari ina mabano ya kushoto katika hasi 4 na shading kwa haki. Suluhisho katika notation ya muda ni hasi 4 hadi infinity ndani ya mabano.$

ⓑ

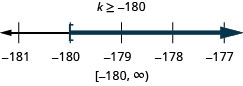
$k ni kubwa kuliko au sawa na hasi 180. Suluhisho kwenye mstari wa nambari ina bracket ya kushoto katika hasi 180 na shading kwa haki. Suluhisho katika maelezo ya muda ni hasi 180 hadi infinity ndani ya bracket na mabano.$

Mfano $\PageIndex{12}$

Tatua kila usawa, graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda:

ⓐ $−7r\leq −70$ ⓑ $\frac{u}{−4}\geq −16$ .

Jibu

ⓐ

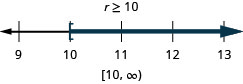
$r ni kubwa kuliko au sawa na 10. Suluhisho kwenye mstari wa nambari ina bracket ya kushoto saa 10 na shading kwa haki. Suluhisho katika notation ya muda ni 10 hadi infinity ndani ya bracket na mabano.$

ⓑ

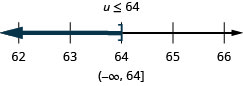
$u ni chini ya au sawa na 64. Suluhisho kwenye mstari wa nambari ina bracket sahihi saa 64 na shading upande wa kushoto. Suluhisho katika notation ya muda ni infinity hasi kwa 64 ndani ya mabano na bracket.$

Ukosefu wa usawa zaidi utachukua hatua zaidi ya moja kutatua. Tunafuata hatua sawa tulizotumia katika mkakati wa jumla wa kutatua equations linear, lakini hakikisha kulipa kipaumbele karibu wakati tunapozidisha au kugawanya ili kutenganisha kutofautiana.

Tatua usawa $6y\leq 11y+17$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

Jibu

	$.$
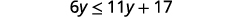
Ondoa 11y11y kutoka pande zote mbili kukusanya vigezo upande wa kushoto.	$.$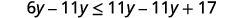
Kurahisisha.	$.$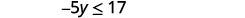
Gawanya pande zote mbili za usawa kwa -5, -5, na urekebishe usawa.	$.$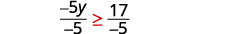
Kurahisisha.	$.$
Grafu suluhisho kwenye mstari wa nambari.	$.$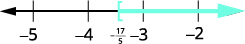
Andika suluhisho katika maelezo ya muda.	$.$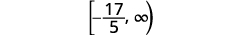

Tatua usawa, graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda: $3q\geq 7q−23$ .

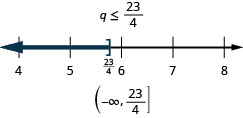
Jibu: $q ni chini ya au sawa na 23 kugawanywa na 4. Suluhisho kwenye mstari wa nambari ina bracket sahihi saa 23 imegawanywa na 4 na shading upande wa kushoto. Suluhisho katika maelezo ya muda ni infinity hasi hadi 23 imegawanywa na 4 ndani ya mabano na bracket.$

Mfano $\PageIndex{15}$

Tatua usawa, graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda: $6x<10x+19$ .

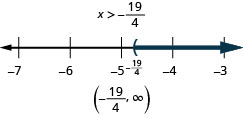
Jibu: $x ni kubwa kuliko hasi 19 imegawanywa na 4. Suluhisho kwenye mstari wa nambari ina mabano ya kushoto katika hasi 19 imegawanywa na 4 na shading kwa haki. Suluhisho katika notation ya muda ni hasi 19 imegawanywa na 4 hadi infinity ndani ya mabano.$

Wakati wa kutatua kutofautiana, kwa kawaida ni rahisi kukusanya vigezo upande ambapo mgawo wa kutofautiana ni mkubwa zaidi. Hii hupunguza coefficients hasi na hivyo hatuna kuzidisha au kugawanya na hasi - ambayo ina maana hatuna kukumbuka kubadili ishara ya usawa.

Mfano $\PageIndex{16}$

Tatua usawa $8p+3(p−12)>7p−28$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

Jibu

	$8p+3(p−12)>7p−28$
Kurahisisha kila upande iwezekanavyo.
Kusambaza.	$8p+3p−36>7p−28$
Kuchanganya kama maneno.	$11p−36>7p−28$
Ondoa $7p$ kutoka pande zote mbili kukusanya vigezo upande wa kushoto, tangu $11>7$ .	$11p−36−7p>7p−28−7p$
Kurahisisha.	$4p−36>−28$
$36$ Ongeza pande zote mbili kukusanya mara kwa mara upande wa kulia.	$4p−36+36>−28+36$
Kurahisisha.	$4p>8$
Gawanya pande zote mbili za usawa na $4$ ; usawa unakaa sawa.	$\dfrac{4p}{4}>\dfrac{8}{4}$
Kurahisisha.	$p>2$
Grafu suluhisho kwenye mstari wa nambari.	$.$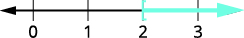
Andika suluhisho katika maelezo ya muda.	$(2,\infty)$

Mfano $\PageIndex{17}$

Tatua usawa $9y+2(y+6)>5y−24$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

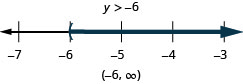
Jibu: $y ni kubwa kuliko hasi 6. Suluhisho kwenye mstari wa nambari ina mabano ya kushoto katika hasi 6 na shading kwa haki. Suluhisho katika notation ya muda ni hasi 6 hadi infinity ndani ya mabano.$

Mfano $\PageIndex{18}$

Tatua usawa $6u+8(u−1)>10u+32$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

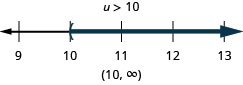
Jibu: $u ni kubwa kuliko hasi 10. Suluhisho kwenye mstari wa nambari ina mabano ya kushoto saa 10 na shading kwa haki. Suluhisho katika maelezo ya muda ni 10 hadi infinity ndani ya mabano.$

Kama vile baadhi ya equations ni utambulisho na baadhi ni utata, kutofautiana inaweza kuwa utambulisho au utata, pia. Tunatambua aina hizi wakati sisi ni wa kushoto na constants tu kama sisi kutatua usawa. Ikiwa matokeo ni taarifa ya kweli, tuna utambulisho. Ikiwa matokeo ni taarifa ya uongo, tuna utata.

Mfano $\PageIndex{19}$

Tatua usawa $8x−2(5−x)<4(x+9)+6x$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

Jibu

Kurahisisha kila upande iwezekanavyo.		$8x−2(5−x)<4(x+9)+6x$
Kusambaza.		$8x−10+2x<4x+36+6x$
Kuchanganya kama maneno.		$10x−10<10x+36$
Ondoa ${\color{red}{10x}}$ kutoka pande zote mbili kukusanya vigezo upande wa kushoto.		$10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}$
Kurahisisha.		$−10<36$
Ya $x$ ni gone, na tuna taarifa ya kweli.		Ukosefu wa usawa ni utambulisho. Suluhisho ni namba zote halisi.
Grafu suluhisho kwenye mstari wa nambari.		$.$
Andika suluhisho katika maelezo ya muda.		$(−\infty,\infty)$

Mfano $\PageIndex{20}$

Tatua usawa $4b−3(3−b)>5(b−6)+2b$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

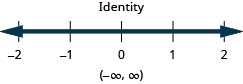
Jibu: $Ukosefu wa usawa ni utambulisho. Suluhisho lake kwenye mstari wa nambari ni kivuli kwa maadili yote. Suluhisho katika notation ya muda ni infinity hasi kwa infinity ndani ya mabano.$

Mfano $\PageIndex{21}$

Tatua usawa $9h−7(2−h)<8(h+11)+8h$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

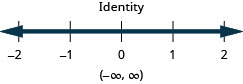
Jibu: $Ukosefu wa usawa ni utambulisho. Suluhisho lake kwenye mstari wa nambari ni kivuli kwa maadili yote. Suluhisho katika notation ya muda ni infinity hasi kwa infinity ndani ya mabano.$

Tunaweza kufuta sehemu ndogo katika kutofautiana kama tulivyofanya katika equations. Tena, kuwa makini na ishara wakati unapozidisha au kugawa kwa hasi.

Mfano $\PageIndex{22}$

Tatua usawa $\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

Jibu

	$\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$
Kuzidisha pande zote mbili na LCD, 24, ili kufuta sehemu ndogo.	${\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)$
Kurahisisha.	$8a - 3a > 5a + 18$
Kuchanganya kama maneno.	$5a > 5a + 18$
Ondoa $5a$ kutoka pande zote mbili kukusanya vigezo upande wa kushoto.	$5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18$
Kurahisisha.	$0 > 18$
Taarifa hiyo ni ya uongo.	Ukosefu wa usawa ni utata. Hakuna suluhisho.
Grafu suluhisho kwenye mstari wa nambari.	$.$
Andika suluhisho katika maelezo ya muda.	Hakuna suluhisho.

Mfano $\PageIndex{23}$

Tatua usawa $\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

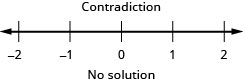
Jibu: $Ukosefu wa usawa ni utata. Kwa hiyo, hakuna suluhisho. Matokeo yake, hakuna grafu kwenye mstari wa nambari au notation ya muda.$

Mfano $\PageIndex{24}$

Tatua usawa $\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}$ , graph suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

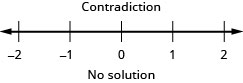
Jibu: $Ukosefu wa usawa ni utata. Kwa hiyo, hakuna suluhisho. Matokeo yake, hakuna grafu kwenye mstari wa nambari au notation ya muda.$

Tafsiri kwa Usawa na Kutatua

Ili kutafsiri sentensi za Kiingereza kwa kutofautiana, tunahitaji kutambua misemo inayoonyesha usawa. Maneno mengine ni rahisi, kama “zaidi ya” na “chini ya.” Lakini wengine si kama dhahiri. Jedwali linaonyesha baadhi ya misemo ya kawaida ambayo yanaonyesha kutofautiana.

$>$	$\geq$	$<$	$\leq$
\ (>\) ">\)” data-valign="middle” class="lt-math-17389">ni kubwa kuliko iliyo kubwa kuliko iliyo kubwa kuliko inazidi	\ (\ geq\)” data-valign="middle">ni kubwa kuliko au sawa na ni angalau si chini ya ni kiwango cha chini	\ ni <\)” data-valign="middle"> chini ya ni ndogo kuliko ina wachache kuliko ni chini kuliko	\ (\ leq\)” data-valign="middle">ni chini ya au sawa na ni kwa zaidi si zaidi ya kiwango cha juu

Mfano $\PageIndex{25}$

Tafsiri na kutatua. Kisha grafu suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

$\text{Twenty-seven less than }x\text{ is at least }48.\nonumber$

Jibu

	$.$
Tafsiri.	$x - 27 \geq 48$
Kutatua - Ongeza 27 kwa pande zote mbili.	$x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}$
Kurahisisha.	$x \geq 75$
Grafu kwenye mstari wa nambari.	$.$
Andika katika notation ya muda.	$[75, \infty)$

Tafsiri na kutatua. Kisha grafu suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

$\text{Nineteen less than } p \text{ is no less than }47.\nonumber$

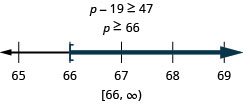
Jibu: $p minus 19 ni kubwa kuliko au sawa na 47. Suluhisho lake ni p ni kubwa kuliko au sawa na 66. Suluhisho kwenye mstari wa nambari ina bracket ya kushoto saa 66 na shading kwa haki. Suluhisho katika maelezo ya muda ni 66 hadi infinity ndani ya bracket na mabano.$

Mfano $\PageIndex{27}$

Tafsiri na kutatua. Kisha grafu suluhisho kwenye mstari wa nambari, na uandike suluhisho katika maelezo ya muda.

$\text{Four more than }a\text{ is at most }15.\nonumber$

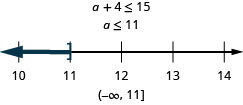
Jibu: $pamoja 4 ni chini ya au sawa na 15. Suluhisho lake ni chini ya au sawa na 11. Suluhisho kwenye mstari wa nambari ina bracket sahihi saa 11na kivuli upande wa kushoto. Suluhisho katika notation ya muda ni infinity hasi kwa 11 ndani ya mabano na bracket.$

Tatua Maombi na Usawa wa Mstari

Hali nyingi za maisha halisi zinahitaji sisi kutatua kutofautiana. Njia tutakayotumia kutatua programu na kutofautiana kwa mstari ni kama ile tuliyotumia wakati tulitatua programu na equations.

Tutasoma tatizo na kuhakikisha maneno yote yanaeleweka. Ifuatayo, tutatambua kile tunachotafuta na kugawa variable ili kuiwakilisha. Tutaelezea tena tatizo katika sentensi moja ili iwe rahisi kutafsiri kwa usawa. Kisha, sisi kutatua kukosekana kwa usawa.

Wakati mwingine maombi inahitaji ufumbuzi kuwa namba nzima, lakini suluhisho la algebraic kwa usawa sio namba nzima. Katika hali hiyo, tunapaswa kuzunguka suluhisho la algebraic kwa idadi nzima. muktadha wa maombi itaamua kama sisi pande zote juu au chini.

Mfano $\PageIndex{28}$

Dawn alishinda ruzuku mini-ya $4,000 kununua kompyuta kibao kwa ajili ya darasa lake. Vidonge ambavyo angependa kununua gharama $254.12 kila mmoja, ikiwa ni pamoja na kodi na utoaji. Nambari ya juu ya vidonge Dawn inaweza kununua nini?

Jibu: $\begin{array} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Choose a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{information to find it.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$4,000.} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15} \\{\text{But }n\text{ must be a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{Rounding down the price to } $250, 15} &{} \\ {\space\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\space\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Answer }\text{the question with a complete sentence.}} &{\text{Dawn can buy a maximum of 15 tablets.}} \\ \end{array}$

Mfano $\PageIndex{29}$

Angie ina $20 kutumia kwenye masanduku ya juisi kwa picnic ya mapema ya mtoto wake. Kila pakiti ya masanduku ya juisi hupunguza $2.63. Nambari ya juu ya pakiti ambazo anaweza kununua ni nini?

Jibu: Angie anaweza kununua pakiti 7 za juisi.

Mfano $\PageIndex{30}$

Daniel anataka kumshangaa mpenzi wake na chama cha kuzaliwa kwenye mgahawa wake unaopenda. Itakuwa gharama $42.75 kwa kila mtu kwa chakula cha jioni, ikiwa ni pamoja na ncha na kodi. Bajeti yake kwa ajili ya chama ni $500. Idadi ya juu ya watu Daniel anaweza kuwa nayo katika chama gani?

Jibu: Danieli anaweza kuwa na watu 11 kwenye chama.

Mfano $\PageIndex{31}$

Mpango wa simu wa Taleisha unamgharimu $28.80 kwa mwezi pamoja na $0.20 kwa kila ujumbe wa maandishi. Jinsi ujumbe wa maandishi wengi anaweza kutuma/kupokea na kuweka simu yake ya kila mwezi muswada si zaidi ya $50?

Jibu: $\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can make}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to represent that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step 4. Translate }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.80+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 0.2t\leq 21.2} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\space\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text messages to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}$

Mfano $\PageIndex{32}$

Sergio na Lizeth wana bajeti ya likizo kali sana. Wanapanga kukodisha gari kutoka kampuni inayoshutumu $75 kwa wiki pamoja na $0.25 kwa maili. Jinsi maili wengi wanaweza kusafiri wakati wa wiki na bado kuweka ndani yao $200 bajeti?

Jibu: Sergio na Lizeth wanaweza kusafiri si zaidi ya maili 500.

Mfano $\PageIndex{33}$

Muswada wa joto wa Rameen ni $5.42 kwa mwezi pamoja na $1.08 kwa therm. Wangapi therms unaweza Rameen kutumia kama anataka muswada wake inapokanzwa kuwa upeo wa $87.50.

Jibu: Muswada wa joto wa Rameen ni $5.42 kwa mwezi pamoja na $1.08 kwa therm. Wangapi therms unaweza Rameen kutumia kama anataka muswada wake inapokanzwa kuwa upeo wa $87.50.

Faida ni pesa iliyobaki wakati gharama zimeondolewa kutoka mapato. Katika mfano unaofuata, tutapata idadi ya ajira ambayo mwanamke mdogo anahitaji kufanya kila mwezi ili kufanya kiasi fulani cha faida.

Mfano $\PageIndex{34}$

Felicity ina biashara ya calligraphy. Yeye mashtaka $2.50 kwa mwaliko harusi. Gharama zake za kila mwezi ni $650. Ni mialiko ngapi lazima aandike ili kupata faida ya angalau $2,800 kwa mwezi?

Jibu: $\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\space\space\space\text{Choose a variable to represent it.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$2.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\space\space\space 2.50j−650\geq 2,800} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 2.5j\geq 3,450} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space j\geq 1,380 \text{ invitations}} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\space\space\space \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\space\space\space $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Felicity must write at least }1,380\text{ invitations.}} \\ \end{array}$

Mfano $\PageIndex{35}$

Caleb ana mnyama ameketi biashara. Yeye mashtaka $32 kwa saa. Gharama zake za kila mwezi ni $2,272. Ni masaa ngapi anapaswa kufanya kazi ili kupata faida ya angalau $800 kwa mwezi?

Jibu: Caleb lazima afanye kazi angalau masaa 96.

Mfano $\PageIndex{36}$

Elliot ina mazingira ya matengenezo ya biashara. Gharama zake za kila mwezi ni $1,100. Ikiwa anadai $60 kwa kazi, ni ajira ngapi lazima afanye ili kupata faida ya angalau $4,000 kwa mwezi?

Jibu: Elliot lazima kazi angalau 85 ajira.

Kuna hali nyingi ambazo kiasi kadhaa huchangia gharama zote. Lazima tuhakikishe akaunti kwa gharama zote za mtu binafsi wakati tunatatua matatizo kama haya.

Mfano $\PageIndex{37}$

Malik anapanga safari ya likizo ya majira ya joto ya siku sita. ana $840 katika akiba, naye chuma $45 kwa saa kwa ajili ya Tutoring. Safari hiyo itamlipa $525 kwa ndege, $780 kwa chakula na kuona, na $95 kwa usiku kwa hoteli. Ni saa ngapi anapaswa kufundisha kuwa na pesa za kutosha kulipa safari?

Jibu: $\begin{array} {ll} {} &{} \\ {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\space \text{Choose a variable to represent that}} &{} \\ {\space\space\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The cost of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must be less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space \text{Translate into an inequality.}} &{525+780+95(6)\leq 840+45h} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,875\leq 840+45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,035\leq 45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 23\leq h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45h} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45(23)} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at least }23\text{ hours.}} \\ \end{array}$

Mfano $\PageIndex{38}$

Brenda rafiki bora ni kuwa marudio harusi na tukio mwisho siku tatu. Brenda ina $500 katika akiba na wanaweza kupata $15 saa babysitting. Anatarajia kulipa dola 350 za ndege, $375 kwa ajili ya chakula na burudani na $60 usiku kwa sehemu yake ya chumba cha hoteli. Ni saa ngapi lazima yeye babysit kuwa na fedha za kutosha kulipa kwa ajili ya safari?

Jibu: Brenda lazima babysit angalau 27 masaa.

Mfano $\PageIndex{39}$

Josue anataka kwenda safari ya barabara ya usiku 10 na marafiki ijayo spring. Itakuwa gharama yake $180 kwa ajili ya gesi, $450 kwa ajili ya chakula, na $49 kwa usiku kushiriki chumba motel. ana $520 katika akiba na wanaweza kupata $30 kwa driveway shoveling theluji. Jinsi driveways wengi lazima yeye koleo kuwa na fedha za kutosha kulipa kwa ajili ya safari?

Jibu: Josue lazima koleo angalau 20 driveways.

Dhana muhimu

Ukosefu wa usawa, Mistari ya Nambari, na Uthibitishaji wa
$x>a \quad x\geq a\quad x<a\quad x\leq a$
$Takwimu inaonyesha kwamba ufumbuzi wa usawa x ni mkubwa kuliko unahitajika kwenye mstari wa namba na mabano ya kushoto kwenye na kivuli kwa haki, na kwamba suluhisho katika nukuu ya muda ni muda kutoka kwa infinity iliyoambatanishwa katika mabano. Inaonyesha ufumbuzi wa kukosekana kwa usawa x ni kubwa kuliko au sawa na unahitajika kwenye mstari namba na mabano kushoto katika na shading na haki, na kwamba ufumbuzi katika muda nukuu ni muda a kwa infinity ndani ya mabano kushoto na mabano haki. Inaonyesha kwamba ufumbuzi wa kukosekana kwa usawa x ni chini ya unahitajika kwenye mstari namba na mabano haki katika na shading upande wa kushoto, na kwamba ufumbuzi katika muda nukuu ni muda infinity hasi kwa ndani ya mabano. Inaonyesha kwamba ufumbuzi wa kukosekana kwa usawa x ni chini ya au sawa na unahitajika kwenye mstari number na mabano haki katika na shading upande wa kushoto, na kwamba ufumbuzi katika muda nukuu ni hasi infinity ndani ya mabano kushoto na mabano haki.$
Ukosefu wa usawa wa mstari
- Ukosefu wa usawa wa mstari ni usawa katika kutofautiana moja ambayo inaweza kuandikwa katika mojawapo ya fomu zifuatazo ambapo a, b, na c ni namba halisi na $a\neq 0$ :
  $ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber$
Kuongeza na Kuondoa Mali ya Ukosefu wa usawa
- Kwa idadi yoyote a, b, na c, kama a<b, basi <b, basi
  $\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber$
- Tunaweza kuongeza au kuondoa kiasi sawa kutoka pande zote mbili za usawa na bado kuweka usawa.
Kuzidisha na Idara ya Mali ya Usawa
- Kwa idadi yoyote a, b, na c,
  $\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}$

Maneno ambayo yanaonyesha kutofautiana

$>$	$\geq$	$<$	$\leq$
\ (>\) "> ni kubwa kuliko ni zaidi ya ni kubwa kuliko unazidi	\ (\ geq\)” data-valign="middle">ni kubwa kuliko au sawa na ni angalau si chini ya ni kiwango cha chini	\ ni <\)” data-valign="middle"> chini ya ni ndogo kuliko ina wachache kuliko ni chini kuliko	\ (\ leq\)” data-valign="middle">ni chini ya au sawa na ni kwa zaidi si zaidi ya kiwango cha juu

Malengo ya kujifunza

Usawa wa Grafu kwenye Mstari wa Idadi

USAWA, MISTARI YA NAMBA, NA NOTATION YA MUDA

Mfano2.6.1\PageIndex{1}

Mfano2.6.3\PageIndex{3}

Mfano2.6.5\PageIndex{5}

Mfano2.6.6\PageIndex{6}

Kutatua Usawa Linear

USAWA WA MSTARI

KUONGEZA NA KUTOA MALI YA KUTOFAUTIANA

KUZIDISHA NA MGAWANYIKO MALI YA USAWA

Mfano2.6.7\PageIndex{7}

Mfano2.6.9\PageIndex{9}

Mfano2.6.10\PageIndex{10}

Mfano2.6.11\PageIndex{11}

Mfano2.6.12\PageIndex{12}

Mfano2.6.15\PageIndex{15}

Mfano2.6.16\PageIndex{16}

Mfano2.6.17\PageIndex{17}

Mfano2.6.18\PageIndex{18}

Mfano2.6.19\PageIndex{19}

Mfano2.6.20\PageIndex{20}

Mfano2.6.21\PageIndex{21}

Mfano2.6.22\PageIndex{22}

Mfano2.6.23\PageIndex{23}

Mfano2.6.24\PageIndex{24}

Tafsiri kwa Usawa na Kutatua

Mfano2.6.25\PageIndex{25}

Mfano2.6.27\PageIndex{27}

Tatua Maombi na Usawa wa Mstari

Mfano2.6.28\PageIndex{28}

Mfano2.6.29\PageIndex{29}

Mfano2.6.30\PageIndex{30}

Mfano2.6.31\PageIndex{31}

Mfano2.6.32\PageIndex{32}

Mfano2.6.33\PageIndex{33}

Mfano2.6.34\PageIndex{34}

Mfano2.6.35\PageIndex{35}

Mfano2.6.36\PageIndex{36}

Mfano2.6.37\PageIndex{37}

Mfano2.6.38\PageIndex{38}

Mfano2.6.39\PageIndex{39}

Dhana muhimu

Mfano $\PageIndex{1}$

Mfano $\PageIndex{3}$

Mfano $\PageIndex{5}$

Mfano $\PageIndex{6}$

Mfano $\PageIndex{7}$

Mfano $\PageIndex{9}$

Mfano $\PageIndex{10}$

Mfano $\PageIndex{11}$

Mfano $\PageIndex{12}$

Mfano $\PageIndex{15}$

Mfano $\PageIndex{16}$

Mfano $\PageIndex{17}$

Mfano $\PageIndex{18}$

Mfano $\PageIndex{19}$

Mfano $\PageIndex{20}$

Mfano $\PageIndex{21}$

Mfano $\PageIndex{22}$

Mfano $\PageIndex{23}$

Mfano $\PageIndex{24}$

Mfano $\PageIndex{25}$

Mfano $\PageIndex{27}$

Mfano $\PageIndex{28}$

Mfano $\PageIndex{29}$

Mfano $\PageIndex{30}$

Mfano $\PageIndex{31}$

Mfano $\PageIndex{32}$

Mfano $\PageIndex{33}$

Mfano $\PageIndex{34}$

Mfano $\PageIndex{35}$

Mfano $\PageIndex{36}$

Mfano $\PageIndex{37}$

Mfano $\PageIndex{38}$

Mfano $\PageIndex{39}$