Skip to main content
Global

1.6E: Mazoezi

  1. Last updated
  2. Save as PDF
  • Page ID
    176185

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mazoezi hufanya kamili

    Tumia Mali za Comutative na Associative

    Katika mazoezi yafuatayo, kurahisisha.

    1. \(43m+(−12n)+(−16m)+(−9n)\)

    Jibu

    \(27m+(−21n)\)

    2. \(−22p+17q+(−35p)+(−27q)\)

    3. \(\frac{3}{8}g+\frac{1}{12}h+\frac{7}{8}g+\frac{5}{12}h\)

    Jibu

    \(\frac{5}{4}g+\frac{1}{2}h\)

    4. \(\frac{5}{6}a+\frac{3}{10}b+\frac{1}{6}a+\frac{9}{10}b\)

    5. \(6.8p+9.14q+(−4.37p)+(−0.88q)\)

    Jibu

    \(2.43p+8.26q\)

    6. \(9.6m+7.22n+(−2.19m)+(−0.65n)\)

    7. \(−24·7·\frac{3}{8}\)

    Jibu

    \(−63\)

    8. \(−36·11·\frac{4}{9}\)

    9. \(\left(\frac{5}{6}+\frac{8}{15}\right)+\frac{7}{15}\)

    Jibu

    \(1\frac{5}{6}\)

    10. \(\left(\frac{11}{12}+\frac{4}{9}\right)+\frac{5}{9}\)

    11. \(17(0.25)(4)\)

    Jibu

    \(17\)

    12. \(36(0.2)(5)\)

    13. \([2.48(12)](0.5)\)

    Jibu

    \(14.88\)

    14. \([9.731(4)](0.75)\)

    15. \(12\left(\frac{5}{6}p\right)\)

    Jibu

    \(10p\)

    16. \(20\left(\frac{3}{5}q\right)\)

    Tumia Mali ya Identity, Inverse na Zero

    Katika mazoezi yafuatayo, kurahisisha.

    17. \(19a+44−19a\)

    Jibu

    \(44\)

    18. \(27c+16−27c\)

    19. \(\frac{1}{2}+\frac{7}{8}+\left(−\frac{1}{2}\right)\)

    Jibu

    \(\frac{7}{8}\)

    20. \(\frac{2}{5}+\frac{5}{12}+\left(−\frac{2}{5}\right)\)

    21. \(10(0.1d)\)

    Jibu

    \(d\)

    22. \(100(0.01p)\)

    23. \(\frac{3}{20}·\frac{49}{11}·\frac{20}{3}\)

    Jibu

    \(\frac{49}{11}\)

    24. \(\frac{13}{18}·\frac{25}{7}·\frac{18}{13}\)

    25. \(\frac{0}{u−4.99}\), wapi\(u\neq 4.99\)

    Jibu

    \(0\)

    26. \(0÷(y−\frac{1}{6})\), wapi\(x \neq 16\)

    27. \(\frac{32−5a}{0}\), wapi\(32−5a\neq 0\)

    Jibu

    haijafafanuliwa

    28. \(\frac{28−9b}{0}\), wapi\(28−9b\neq 0\)

    29. \(\left(\frac{3}{4}+\frac{9}{10}m\right)÷0\), wapi\(\frac{3}{4}+\frac{9}{10}m\neq 0\)

    Jibu

    haijafafanuliwa

    30. \(\left(\frac{5}{16}n−\frac{3}{7}\right)÷0\), wapi\(\frac{5}{16}n−\frac{3}{7}\neq 0\)

    Rahisisha Maneno Kutumia Mali ya Kusambaza

    Katika mazoezi yafuatayo, kurahisisha kutumia Mali ya Usambazaji.

    31. \(8(4y+9)\)

    Jibu

    \(32y+72\)

    32. \(9(3w+7)\)

    33. \(6(c−13)\)

    Jibu

    \(6c−78\)

    34. \(7(y−13)\)

    35. \(\frac{1}{4}(3q+12)\)

    Jibu

    \(\frac{3}{4}q+3\)

    36. \(\frac{1}{5}(4m+20)\)

    37. \(9(\frac{5}{9}y−\frac{1}{3})\)

    Jibu

    \(5y−3\)

    38. \(10(\frac{3}{10}x−\frac{2}{5})\)

    39. \(12(\frac{1}{4}+\frac{2}{3}r)\)

    Jibu

    \(3+8r\)

    40. \(12(\frac{1}{6}+\frac{3}{4}s)\)

    41. \(15⋅\frac{3}{5}(4d+10)\)

    Jibu

    \(36d+90\)

    42. \(18⋅\frac{5}{6}(15h+24)\)

    43. \(r(s−18)\)

    Jibu

    \(rs−18r\)

    44. \(u(v−10)\)

    45. \((y+4)p\)

    Jibu

    \(yp+4p\)

    46. \((a+7)x\)

    47. \(−7(4p+1)\)

    Jibu

    \(−28p−7\)

    48. \(−9(9a+4)\)

    49. \(−3(x−6)\)

    Jibu

    \(−3x+18\)

    50. \(−4(q−7)\)

    51. \(−(3x−7)\)

    Jibu

    \(−3x+7\)

    52. \(−(5p−4)\)

    53. \(16−3(y+8)\)

    Jibu

    \(−3y−8\)

    54. \(18−4(x+2)\)

    55. \(4−11(3c−2)\)

    Jibu

    \(−33c+26\)

    56. \(9−6(7n−5)\)

    57. \(22−(a+3)\)

    Jibu

    \(−a+19\)

    58. \(8−(r−7)\)

    59. \((5m−3)−(m+7)\)

    Jibu

    \(4m−10\)

    60. \((4y−1)−(y−2)\)

    61. \(9(8x−3)−(−2)\)

    Jibu

    \(72x−25\)

    62. \(4(6x−1)−(−8)\)

    63. \(5(2n+9)+12(n−3)\)

    Jibu

    \(22n+9\)

    64. \(9(5u+8)+2(u−6)\)

    65. \(14(c−1)−8(c−6)\)

    Jibu

    \(6c+34\)

    66. \(11(n−7)−5(n−1)\)

    67. \(6(7y+8)−(30y−15)\)

    Jibu

    \(12y+63\)

    68. \(7(3n+9)−(4n−13)\)

    Mazoezi ya kuandika

    69. Kwa maneno yako mwenyewe, sema Mali ya Associative ya kuongeza.

    Jibu

    Majibu yatatofautiana.

    70. Ni tofauti gani kati ya inverse ya kuongezea na inverse ya multiplicative ya idadi

    71. Kurahisisha\(8(x−\frac{1}{4})\) kutumia Mali Distributive na kueleza kila hatua.

    Jibu

    Majibu yatatofautiana.

    72. Eleza jinsi unavyoweza kuzidisha\(4($5.97)\) bila karatasi au calculator kwa kufikiria\($5.97\) kama\(6−0.03\) na kisha kutumia Mali ya Usambazaji.

    Self Check

    Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

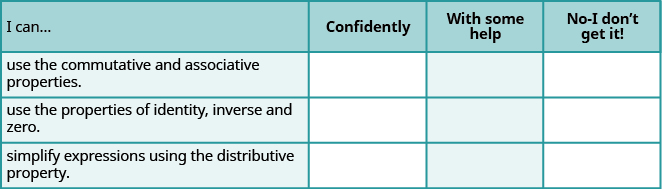
    Jedwali hili lina nguzo 4, safu 3 na mstari wa kichwa. Mstari wa kichwa huandika kila safu ninayoweza, kwa ujasiri, kwa msaada na hapana, siipati. Safu ya kwanza ina kauli zifuatazo: tumia mali za kubadilisha na za ushirika, tumia mali ya utambulisho, inverse na sifuri, kurahisisha maneno kwa kutumia Mali ya Distributive. Nguzo zilizobaki ni tupu.

    b Baada ya kuchunguza orodha hii, utafanya nini ili uwe na ujasiri kwa malengo yote?