Sura ya 1 Mazoezi Mapitio

Sura ya Mapitio ya mazoezi

Tumia Lugha ya Algebra

Tambua Multiples na Mambo

1. Tumia vipimo vya mgawanyiko ili kuamua kama 180 inagawanyika na 2, na 3, na 5, na 6, na kwa 10.

Jibu

Imegawanyika na$2,3,5,6$

2. Kupata factorization mkuu wa 252.

3. Kupata angalau ya kawaida nyingi ya 24 na 40.

Jibu

120

Katika mazoezi yafuatayo, kurahisisha kila kujieleza.

4. $24÷3+4(5−2)$

5. $7+3[6−4(5−4)]−3^2$

Jibu

4

Tathmini ya Kuelezea

Katika mazoezi yafuatayo, tathmini maneno yafuatayo.

6. Wakati$x=4$, ⓐ $x^3$ ⓑ $5x$ ⓒ $2x^2−5x+3$

7. $2x^2−4xy−3y^2$lini$x=3$ na$y=1$

Jibu

3

Kurahisisha Maneno kwa Kuchanganya Kama Masharti

Katika mazoezi yafuatayo, kurahisisha maneno yafuatayo kwa kuchanganya maneno kama hayo.

8. $12y+7+2y−5$

9. $14x^2−9x+11−8x^2+8x−6$

Jibu

$6x^2−x+5$

Tafsiri Maneno ya Kiingereza kwa kujieleza kwa Kialgebraic

Katika mazoezi yafuatayo, tafsiri maneno katika maneno ya algebraic.

10. ⓐ jumla ya$4ab^2$$7a3b24ab^2$ na$7a^3b^2$

ⓑ bidhaa ya$6y^2$ na$3y$

ⓒ kumi na mbili zaidi$5x$

ⓓ$5y$ chini ya$8y^2$

11. ⓐ mara kumi na moja tofauti ya$y$ na mbili

ⓑ tofauti ya mara kumi na moja$y$ na mbili

Jibu

ⓐ$11(y−2)$
ⓑ$11y−2$

12. Dushko ina nickels na pennies katika mfuko wake. Idadi ya pennies ni nne chini ya tano idadi ya nickels. Hebu nn kuwakilisha idadi ya nickels. Andika maneno kwa idadi ya pennies.

Nambari kamili

Kurahisisha Maneno na Thamani kamili

Katika zoezi zifuatazo, jaza$<,>,$ au$=$ kwa kila jozi zifuatazo za namba.

13. ⓐ$−|7| \_\_\_−|−7|$

ⓑ$−8 \_\_\_−|−8|$

ⓒ$|−13| \_\_\_−13$

ⓓ$|−12| \_\_\_−(−12)$

Jibu

ⓐ$=$
ⓑ$=$
ⓒ$>$
ⓓ$=$

Katika mazoezi yafuatayo, kurahisisha.

14. $9−|3(4−8)|$

15. $12−3|1−4(4−2)|$

Jibu

$−9$

Kuongeza na Ondoa Integers

Katika mazoezi yafuatayo, kurahisisha kila kujieleza.

16. $−12+(−8)+7$

17. ⓐ$15−7$

ⓑ$−15−(−7)$

ⓒ$−15−7$

ⓓ$15−(−7)$

Jibu

ⓐ$8$
ⓑ$−8$
ⓒ$−22$
ⓓ$22$

18. $−11−(−12)+5$

19. ⓐ$23−(−17)$ ⓑ$23+17$

Jibu

ⓐ 40 ⓑ 40

20. $−(7−11)−(3−5)$

Kuzidisha na Gawanya Integers

Katika zoezi zifuatazo, kuzidisha au kugawanya.

21. ⓐ$−27÷9$ ⓑ$120÷(−8)$ ⓒ$4(−14)$ ⓓ$−1(−17)$

Jibu

ⓐ$−3$ ⓑ$−15$ ⓒ$−56$ ⓓ$17$

Kurahisisha na Tathmini Maneno na Integers

Katika mazoezi yafuatayo, kurahisisha kila kujieleza.

22. ⓐ$(−7)^3$ ⓑ$−7^3$

23. $(7−11)(6−13)$

Jibu

16

24. $63÷(−9)+(−36)÷(−4)$

25. $6−3|4(1−2)−(7−5)|$

Jibu

$−12$

26. $(−2)^4−24÷(13−5)$

Kwa mazoezi yafuatayo, tathmini kila kujieleza.

27. $(y+z)^2$lini$y=−4$ na$z=7$

Jibu

9

28. $3x^2−2xy+4y^2$lini$x=−2$ na$y=−3$

Tafsiri Maneno ya Kiingereza kwa Maneno ya Algebraic

Katika mazoezi yafuatayo, tafsiri kwa kujieleza kwa algebraic na kurahisisha ikiwa inawezekana.

29. jumla ya$−4$ na$−9$, iliongezeka kwa$23$

Jibu

$(−4+(−9))+23;10$

30. ⓐ tofauti ya 17 na -8 ⓑ Ondoa 17 kutoka -25

Tumia Integers katika Maombi

Katika zoezi zifuatazo, tatua.

31. Joto Mnamo Julai 10, halijoto ya juu huko Phoenix, Arizona, ilikuwa 109°, na halijoto ya juu mnamo Juneau, Alaska, ilikuwa 63°. Ni tofauti gani kati ya joto katika Palm Springs na joto huko Whitefield?

Jibu

$46°$

FRACTIONS

Kurahisisha Fractions

Katika mazoezi yafuatayo, kurahisisha.

32. $\dfrac{204}{228}$

33. $−\dfrac{270x^3}{198y^2}$

Jibu

$−\dfrac{15x^3}{11y^2}$

Kuzidisha na Kugawanya sehemu

Katika mazoezi yafuatayo, fanya operesheni iliyoonyeshwa.

34. $\left(−\dfrac{14}{15}\right)\left(\dfrac{10}{21}\right)$

35. $\dfrac{6x}{25}÷\dfrac{9y}{20}$

Jibu

$\dfrac{8x}{15y}$

36. $\dfrac{−\frac{4}{9}}{\dfrac{8}{21}}$

Ongeza na Ondoa sehemu

Katika mazoezi yafuatayo, fanya operesheni iliyoonyeshwa.

37. $\dfrac{5}{18}+\dfrac{7}{12}$

Jibu

$\dfrac{31}{36}$

38. $\dfrac{11}{36}−\dfrac{15}{48}$

39. ⓐ$\dfrac{5}{8}+\dfrac{3}{4}$ ⓑ$\dfrac{5}{8}÷\dfrac{3}{4}$

Jibu

ⓐ$\dfrac{11}{8}$ ⓑ$\dfrac{5}{6}$

40. ⓐ$−\dfrac{3y}{10}−\dfrac{5}{6}$ ⓑ$−\dfrac{3y}{10}·\dfrac{5}{6}$

Tumia Utaratibu wa Uendeshaji ili kurahisisha Fractions

Katika mazoezi yafuatayo, kurahisisha.

41. $\dfrac{4·3−2·5}{−6·3+2·3}$

Jibu

$−\dfrac{1}{6}$

42. $\dfrac{4(7−3)−2(4−9)}{−3(4+2)+7(3−6)}$

43. $\dfrac{4^3−4^2}{(\dfrac{4}{5})^2}$

Jibu

75

Tathmini Maneno ya kutofautiana na FRACTIONS

Katika mazoezi yafuatayo, tathmini.

44. $4x^2y^2$lini$x=\dfrac{2}{3}$ na$y=−\dfrac{3}{4}$

45. $\dfrac{a+b}{a−b}$lini$a=−4$ na$b=6$

Jibu

$−15$

Desimali

Decimals pande zote

46. $6.738$Pande zote kwa karibu ⓐ mia ⓑ kumi ⓒ idadi nzima.

Kuongeza na Ondoa Decimals

Katika mazoezi yafuatayo, fanya operesheni iliyoonyeshwa.

47. $−23.67+29.84$

Jibu

$6.17$

48. $54.3−100$

49. $79.38−(−17.598)$

Jibu

$96.978$

Kuzidisha na Gawanya Decimals

Katika mazoezi yafuatayo, fanya operesheni iliyoonyeshwa.

50. $(−2.8)(3.97)$

51. $(−8.43)(−57.91)$

Jibu

488.1813

52. $(53.48)(10)$

53. $(0.563)(100)$

Jibu

$56.3$

54. $\$ 118.35÷2.6$

55. $1.84÷(−0.8)$

Jibu

$−23$

Geuza Decimals, Fractions na asilimia

Katika mazoezi yafuatayo, andika kila decimal kama sehemu.

56. $\dfrac{13}{20}$

57. $−\dfrac{240}{25}$

Jibu

$−9.6$

Katika mazoezi yafuatayo, kubadilisha kila sehemu kwa decimal.

58. $−\dfrac{5}{8}$

59. $\dfrac{14}{11}$

Jibu

$1.\overline{27}$

Katika mazoezi yafuatayo, kubadilisha kila decimal kwa asilimia.

60. $2.43$

61. $0.0475$

Jibu

$4.75 \%$

Punguza Maneno na Mizizi ya Mraba

Katika mazoezi yafuatayo, kurahisisha.

62. $\sqrt{289}$

63. $\sqrt{−121}$

Jibu

hakuna idadi halisi

Tambua Integers, Nambari za busara, Hesabu zisizofaa, na Hesabu halisi

Katika zoezi zifuatazo, orodha ya ⓐ namba nzima ⓑ integers ⓒ namba za busara ⓓ namba zisizo na maana ⓔ namba halisi kwa kila seti ya namba

64. $−8,0,1.95286...,\dfrac{12}{5},\sqrt{36},9$

Pata sehemu ndogo na Decimals kwenye Mstari wa Idadi

Katika mazoezi yafuatayo, Pata namba kwenye mstari wa nambari.

65. $\dfrac{3}{4},−\dfrac{3}{4},1\dfrac{1}{3},−1\dfrac{2}{3},\dfrac{7}{2},−\dfrac{5}{2}$

Jibu

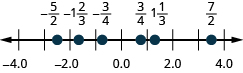
66. ⓐ$3.2$ ⓑ$−1.35$

Mali ya Hesabu halisi

Tumia Mali za Comutative na Associative

Katika mazoezi yafuatayo, kurahisisha.

67. $\dfrac{5}{8}x+\dfrac{5}{12}y+\dfrac{1}{8}x+\dfrac{7}{12}y$

Jibu

$\dfrac{3}{4}x+y$

68. $−32·9·\dfrac{5}{8}$

69. $\left(\dfrac{11}{15}+\dfrac{3}{8}\right)+\dfrac{5}{8}$

Jibu

$1\dfrac{11}{15}$

Tumia Mali ya Identity, Inverse na Zero

Katika mazoezi yafuatayo, kurahisisha.

70. $\dfrac{4}{7}+\dfrac{8}{15}+\left(−\dfrac{4}{7}\right)$

71. $\dfrac{13}{15}·\dfrac{9}{17}·\dfrac{15}{13}$

Jibu

$\dfrac{9}{17}$

72. $\dfrac{0}{x−3},x\neq 3$

73. $\dfrac{5x−7}{0},5x−7\neq 0$

Jibu

haijafafanuliwa

Kurahisisha Maneno Kutumia Mali ya Usambazaji

Katika mazoezi yafuatayo, kurahisisha kutumia Mali ya Usambazaji.

74. $8(a−4)$

75. $12\left(\dfrac{2}{3}b+\dfrac{5}{6}\right)$

Jibu

$8b+10$

76. $18·\dfrac{5}{6}(2x−5)$

77. $(x−5)p$

Jibu

$xp−5p$

78. $−4(y−3)$

79. $12−6(x+3)$

Jibu

$−6x−6$

80. $6(3x−4)−(−5)$

81. $5(2y+3)−(4y−1)$

Jibu

$y+16$

Mazoezi mtihani

1. Kupata factorization mkuu wa$756$.

2. Kuchanganya kama maneno:$5n+8+2n−1$

Jibu

$7n+7$

3. Tathmini lini$x=−2$ na$y=3: \dfrac{|3x−4y|}{6}$

4. Tafsiri kwa kujieleza algebraic na kurahisisha:

ⓐ kumi na moja chini ya nane hasi

ⓑ tofauti ya$−8$ na$−3$, iliongezeka kwa 5

Jibu

$−8−11 = −19$
$(−8−(−3))+5 = 0$

5. Dushko ina nickels na pennies katika mfuko wake. Idadi ya pennies ni saba chini ya mara nne idadi ya nickels. Hebu nn kuwakilisha idadi ya nickels. Andika maneno kwa idadi ya pennies.

6. $28.1458$Pande zote kwa karibu

ⓐ mia ⓑ elfu

Jibu

ⓐ$28.15$ ⓑ$28.146$

7. Geuza

ⓐ$\dfrac{5}{11}$ kwa decimal ⓑ$1.15$ kwa asilimia

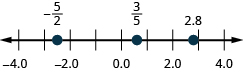
8. Machapisho$\dfrac{3}{5},2.8,and−\dfrac{5}{2}$ kwenye mstari namba.

Jibu

Katika mazoezi yafuatayo, kurahisisha kila kujieleza.

9. $8+3[6−3(5−2)]−4^2$

10. $−(4−9)−(9−5)$

Jibu

1

11. $56÷(−8)+(−27)÷(−3)$

12. $16−2|3(1−4)−(8−5)|$

Jibu

$−8$

13. $−5+2(−3)^2−9$

14. $\dfrac{180}{204}$

Jibu

$\dfrac{15}{17}$

15. $−\dfrac{7}{18}+\dfrac{5}{12}$

16. $\dfrac{4}{5}÷(−\dfrac{12}{25})$

Jibu

$−\dfrac{5}{3}$

17. $\dfrac{9−3·9}{15−9}$

18. $\dfrac{4(−3+2(3−6))}{3(11−3(2+3))}$

Jibu

$3$

19. $\dfrac{5}{13}⋅\dfrac{4}{7}⋅\dfrac{13}{5}$

20. $\dfrac{−\dfrac{5}{9}}{\dfrac{10}{21}}$

Jibu

$−\dfrac{7}{6}$

21. $−4.8+(−6.7)$

22. $34.6−100$

Jibu

$−65.4$

23. $−12.04⋅(4.2)$

24. $−8÷0.05$

Jibu

160

25. $−\sqrt{121}$

26. $(\dfrac{8}{13}+\dfrac{5}{7})+\dfrac{2}{7}$

Jibu

$1\dfrac{8}{13}$

27. $5x+(−8y)−6x+3y$

28. ⓐ$\dfrac{0}{9}$ ⓑ$\dfrac{11}{0}$

Jibu

ⓐ 0 ⓑ haijafafanuliwa

29. $−3(8x−5)$

30. $6(3y−1)−(5y−3)$

Jibu

$13y−3$