1.4E: Mazoezi

Last updated
Save as PDF

Page ID: 176144

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Mazoezi hufanya kamili

Kurahisisha sehemu

Katika mazoezi yafuatayo, kurahisisha.

1. $−\dfrac{108}{63}$

Jibu: $−\dfrac{12}{7}$

2. $−\dfrac{104}{48}$

3. $\dfrac{120}{252}$

Jibu: $\dfrac{10}{21}$

4. $\dfrac{182}{294}$

5. $\dfrac{14x^2}{21y}$

Jibu: $\dfrac{2x^2}{3y}$

6. $\dfrac{24a}{32b^2}$

7. $−\dfrac{210a^2}{110b^2}$

Jibu: $−\dfrac{21a^2}{11b^2}$

8. $−\dfrac{30x^2}{105y^2}$

Kuzidisha na Kugawanya sehemu

Katika mazoezi yafuatayo, fanya operesheni iliyoonyeshwa.

9. $−\dfrac{3}{4}\left(−\dfrac{4}{9}\right)$

Jibu: $\dfrac{1}{3}$

10. $−\dfrac{3}{8}⋅\dfrac{4}{15}$

11. $\left(−\dfrac{14}{15}\right)\left(\dfrac{9}{20}\right)$

Jibu: $−\dfrac{21}{50}$

12. $\left(−\dfrac{9}{10}\right)\left(\dfrac{25}{33}\right)$

13. $\left(−\dfrac{63}{84}\right)\left(−\dfrac{44}{90}\right)$

Jibu: $\dfrac{11}{30}$

14. $\left(−\dfrac{33}{60}\right)\left(−\dfrac{40}{88}\right)$

15. $\dfrac{3}{7}⋅21n$

Jibu: $9n$

16. $\dfrac{5}{6}⋅30m$

17. $\dfrac{3}{4}÷\dfrac{x}{11}$

Jibu: $\dfrac{33}{4x}$

18. $\dfrac{2}{5}÷\dfrac{y}{9}$

19. $\dfrac{5}{18}÷\left(−\dfrac{15}{24}\right)$

Jibu: $−\dfrac{4}{9}$

20. $\dfrac{7}{18}÷\left(−\dfrac{14}{27}\right)$

21. $\dfrac{8u}{15}÷\dfrac{12v}{25}$

Jibu: $\dfrac{10u}{9v}$

22. $\dfrac{12r}{25}÷\dfrac{18s}{35}$

23. $\dfrac{3}{4}÷(−12)$

Jibu: $−\dfrac{1}{16}$

24. $−15÷\left(−\dfrac{5}{3}\right)$

Katika mazoezi yafuatayo, kurahisisha.

25. $−\dfrac{\dfrac{8}{21} }{\dfrac{12}{35}}$

Jibu: $−\dfrac{10}{9}$

26. $− \dfrac{\dfrac{9}{16} }{\dfrac{33}{40}}$

27. $−\dfrac{\dfrac{4}{5}}{2}$

Jibu: $−\dfrac{2}{5}$

28. $\dfrac{\dfrac{5}{3}}{10}$

29. $\dfrac{\dfrac{m}{3}}{\dfrac{n}{2}}$

Jibu: $\dfrac{2m}{3n}$

30. $\dfrac{−\dfrac{3}{8}}{−\dfrac{y}{12}}$

Kuongeza na Ondoa Fractions

Katika mazoezi yafuatayo, ongeza au uondoe.

31. $\dfrac{7}{12}+\dfrac{5}{8}$

Jibu: $\dfrac{29}{24}$

32. $\dfrac{5}{12}+\dfrac{3}{8}$

33. $\dfrac{7}{12}−\dfrac{9}{16}$

Jibu: $\dfrac{1}{48}$

34. $\dfrac{7}{16}−\dfrac{5}{12}$

35. $−\dfrac{13}{30}+\dfrac{25}{42}$

Jibu: $\dfrac{17}{105}$

36. $−\dfrac{23}{30}+\dfrac{5}{48}$

37. $−\dfrac{39}{56}−\dfrac{22}{35}$

Jibu: $−\dfrac{53}{40}$

38. $−\dfrac{33}{49}−\dfrac{18}{35}$

39. $−\dfrac{2}{3}−\left(−\dfrac{3}{4}\right)$

Jibu: $\dfrac{1}{12}$

40. $−\dfrac{3}{4}−\left(−\dfrac{4}{5}\right)$

41. $\dfrac{x}{3}+\dfrac{1}{4}$

Jibu: $\dfrac{4x+3}{12}$

42. $\dfrac{x}{5}−\dfrac{1}{4}$

43. ⓐ$\dfrac{2}{3}+\dfrac{1}{6}$

ⓑ$\dfrac{2}{3}÷\dfrac{1}{6}$

Jibu: ⓐ$\dfrac{5}{6}$ ⓑ$4$

44. ⓐ$−\dfrac{2}{5}−\dfrac{1}{8}$

ⓑ$−\dfrac{2}{5}·\dfrac{1}{8}$

45. ⓐ$\dfrac{5n}{6}÷\dfrac{8}{15}$

ⓑ$\dfrac{5n}{6}−\dfrac{8}{15}$

Jibu: ⓐ$\dfrac{25n}{16}$ ⓑ$\dfrac{25n−16}{30}$

46. ⓐ$\dfrac{3a}{8}÷\dfrac{7}{12}$

ⓑ$\dfrac{3a}{8}−\dfrac{7}{12}$

47. ⓐ$−\dfrac{4x}{9}−\dfrac{5}{6}$

ⓑ$−\dfrac{4k}{9}⋅\dfrac{5}{6}$

Jibu: ⓐ$\dfrac{−8x−15}{18}$ ⓑ$−\dfrac{10k}{27}$

48. ⓐ$−\dfrac{3y}{8}−\dfrac{4}{3}$

ⓑ$−\dfrac{3y}{8}⋅\dfrac{4}{3}$

49. ⓐ$−\dfrac{5a}{3}+\left(−\dfrac{10}{6}\right)$

ⓑ$−\dfrac{5a}{3}÷\left(−\dfrac{10}{6}\right)$

Jibu: ⓐ$\dfrac{−5(a+1)}{3}$ ⓑ$a$

50. ⓐ$\dfrac{2b}{5}+\dfrac{8}{15}$

ⓑ$\dfrac{2b}{5}÷\dfrac{8}{15}$

Tumia Utaratibu wa Uendeshaji ili kurahisisha sehemu ndogo

Katika mazoezi yafuatayo, kurahisisha.

51. $\dfrac{5⋅6−3⋅4}{4⋅5−2⋅3}$

Jibu: $\dfrac{9}{7}$

52. $\dfrac{8⋅9−7⋅6}{5⋅6−9⋅2}$

53. $\dfrac{5^2−3^2}{3−5}$

Jibu: $−8$

54. $\dfrac{6^2−4^2}{4−6}$

55. $\dfrac{7⋅4−2(8−5)}{9⋅3−3⋅5}$

Jibu: $\dfrac{11}{6}$

56. $\dfrac{9⋅7−3(12−8)}{8⋅7−6⋅6}$

57. $\dfrac{9(8−2)−3(15−7)}{6(7−1)−3(17−9)}$

Jibu: $\dfrac{5}{2}$

58. $\dfrac{8(9−2)−4(14−9)}{7(8−3)−3(16−9)}$

59. $\dfrac{2^3+4^2}{\left(\dfrac{2}{3}\right)^2}$

Jibu: $54$

60. $\dfrac{3^3−3^2}{\left(\dfrac{3}{4}\right)^2}$

61. $\dfrac{\left(\dfrac{3}{5}\right)^2}{\left(\dfrac{3}{7}\right)^2}$

Jibu: $\dfrac{49}{25}$

62. $\dfrac{\left(\dfrac{3}{4}\right)^2}{\left(\dfrac{5}{8}\right)^2}$

63. $\dfrac{2}{\dfrac{1}{3}+\dfrac{1}{5}}$

Jibu: $\dfrac{15}{4}$

64. $\dfrac{5}{\dfrac{1}{4}+\dfrac{1}{3}}$

65. $\dfrac{\dfrac{7}{8}−\dfrac{2}{3}}{\dfrac{1}{2}+\dfrac{3}{8}}$

Jibu: $\dfrac{5}{21}$

66. $\dfrac{\dfrac{3}{4}−\dfrac{3}{5}}{\dfrac{1}{4}+\dfrac{2}{5}}$

Mazoezi ya mchanganyiko

Katika mazoezi yafuatayo, kurahisisha.

67. $−\dfrac{3}{8}÷\left(−\dfrac{3}{10}\right)$

Jibu: $\dfrac{5}{4}$

68. $−\dfrac{3}{12}÷\left(−\dfrac{5}{9}\right)$

69. $−\dfrac{3}{8}+\dfrac{5}{12}$

Jibu: $\dfrac{1}{24}$

70. $−\dfrac{1}{8}+\dfrac{7}{12}$

71. $−\dfrac{7}{15}−\dfrac{y}{4}$

Jibu: $\dfrac{−28−15y}{60}$

72. $−\dfrac{3}{8}−\dfrac{x}{11}$

73. $\dfrac{11}{12a}⋅\dfrac{9a}{16}$

Jibu: $\dfrac{33}{64}$

74. $\dfrac{10y}{13}⋅\dfrac{8}{15y}$

75. $\dfrac{1}{2}+\dfrac{2}{3}⋅\dfrac{5}{12}$

Jibu: $\dfrac{7}{9}$

76. $\dfrac{1}{3}+\dfrac{2}{5}⋅\dfrac{3}{4}$

77. $1−\dfrac{3}{5}÷\dfrac{1}{10}$

Jibu: $−5$

78. $1−\dfrac{5}{6}÷\dfrac{1}{12}$

79. $\dfrac{3}{8}−\dfrac{1}{6}+\dfrac{3}{4}$

Jibu: $\dfrac{23}{24}$

80. $\dfrac{2}{5}+\dfrac{5}{8}−\dfrac{3}{4}$

81. $12\left(\dfrac{9}{20}−\dfrac{4}{15}\right)$

Jibu: $\dfrac{11}{5}$

82. $8\left(\dfrac{15}{16}−\dfrac{5}{6}\right)$

83. $\dfrac{\dfrac{5}{8}+\dfrac{1}{6}}{\dfrac{19}{24}}$

Jibu: $1$

84. $\dfrac{\dfrac{1}{6}+\dfrac{3}{10}}{\dfrac{14}{30}}$

85. $\left(\dfrac{5}{9}+\dfrac{1}{6}\right)÷\left(\dfrac{2}{3}−\dfrac{1}{2}\right)$

Jibu: $\dfrac{13}{3}$

86. $\left(\dfrac{3}{4}+\dfrac{1}{6}\right)÷\left(\dfrac{5}{8}−\dfrac{1}{3}\right)$

Tathmini Maneno ya kutofautiana na FRACTIONS

Katika mazoezi yafuatayo, tathmini.

87. $\dfrac{7}{10}−w$wakati ⓐ$w=\dfrac{1}{2}$ ⓑ$w=−\dfrac{1}{2}$

Jibu: ⓐ$\dfrac{1}{5}$ ⓑ$\dfrac{6}{5}$

88. $512−w$wakati ⓐ$w=\dfrac{1}{4}$ ⓑ$w=−\dfrac{1}{4}$

89. $2x^2y^3$lini$x=−\dfrac{2}{3}$ na$y=−\dfrac{1}{2}$

Jibu: $−\dfrac{1}{9}$

90. $8u^2v^3$lini$u=−\dfrac{3}{4}$ na$v=−\dfrac{1}{2}$

91. $\dfrac{a+b}{a−b}$lini$a=−3$ na$b=8$

Jibu: $−\dfrac{5}{11}$

92. $\dfrac{r−s}{r+s}$lini$r=10$ na$s=−5$

Mazoezi ya kuandika

93. Kwa nini unahitaji denominator ya kawaida ili kuongeza au kuondoa sehemu ndogo? Eleza.

Jibu: Majibu yatatofautiana.

94. Je, unapataaje LCD ya vipande viwili?

95. Eleza jinsi unavyopata usawa wa sehemu.

Jibu: Majibu yatatofautiana.

96. Eleza jinsi unavyopata usawa wa nambari hasi.

Self Check

ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

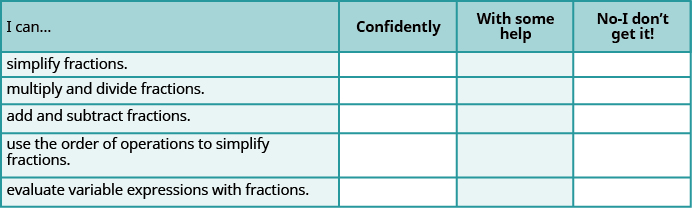
$Jedwali hili lina nguzo 4, safu 5 na mstari wa kichwa. Mstari wa kichwa huandika kila safu ninayoweza, kwa ujasiri, kwa msaada na hapana, siipati. Safu ya kwanza ina kauli zifuatazo: kurahisisha vipande, kuzidisha na kugawanya sehemu ndogo, kuongeza na kuondoa sehemu ndogo, tumia utaratibu wa shughuli ili kurahisisha sehemu ndogo, kutathmini maneno ya kutofautiana na sehemu ndogo. Nguzo zilizobaki ni tupu.$

ⓑ Orodha hii inakuambia nini kuhusu ujuzi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?