1.5: Decimals

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Duru ya decimals
• Ongeza na uondoe decimals
• Kuzidisha na kugawanya decimals
• Badilisha decimals, fractions, na percents
• Punguza maneno na mizizi ya mraba
• Tambua integers, namba za busara, nambari zisizo na maana, na namba halisi
• Pata sehemu ndogo na decimals kwenye mstari wa nambari

Utangulizi wa kina zaidi wa mada yaliyofunikwa katika sehemu hii unaweza kupatikana katika sura ya Elementary Algebra, Misingi.

Decimals pande zote

Decimals ni njia nyingine ya kuandika sehemu ambazo denominators ni nguvu ya kumi.

\[\begin{array}{rcll} 0.1 & = & \dfrac{1}{10} & \text{is “one tenth”} \\ 0.01 & = & \dfrac{1}{100} & \text{is “one hundredth”} \\ 0.001 & = & \dfrac{1}{1000} & \text{is “one thousandth”} \\ 0.0001 & = & \dfrac{1}{10,000} & \text{is “one ten-thousandth”} \end{array}\]

Kama ilivyo kwa idadi nzima, kila tarakimu ya decimal inalingana na thamani ya mahali kulingana na nguvu za kumi. Kielelezo kinaonyesha majina ya maadili ya mahali upande wa kushoto na wa kulia wa hatua ya decimal.

Kielelezo 1.

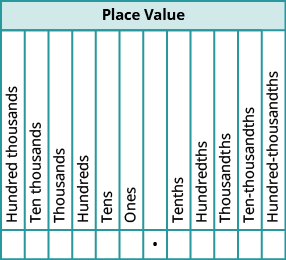
Tunapofanya kazi na decimals, mara nyingi ni muhimu kuzunguka nambari kwa thamani ya karibu ya mahali. Sisi muhtasari hatua za kuzunguka decimal hapa.

DESIMALS PANDE ZOTE.

1. Pata thamani ya mahali uliyopewa na uiangalie kwa mshale.
2. Weka tarakimu kwa haki ya thamani ya mahali.
3. Je, tarakimu iliyopigwa mstari ni kubwa kuliko au sawa na 5?
   • Ndiyo: ongeza 1 kwa tarakimu katika thamani ya mahali uliyopewa.
   • Hapana: usibadili tarakimu katika thamani ya mahali uliyopewa
4. Andika upya nambari, uondoe tarakimu zote kwa haki ya tarakimu inayozunguka.

MFANO\(\PageIndex{1}\)

\(18.379\)Pande zote kwa karibu ⓐ mia ⓑ kumi ⓒ idadi nzima.

Jibu

Round\(18.379.\)

ⓐ kwa karibu mia

Machapisho mahali hundredths na mshale.
Weka tarakimu kwa haki ya thamani ya mahali.
Kwa sababu 9 ni kubwa kuliko au sawa na 5, kuongeza 1 kwa 7.
Andika upya nambari, uondoe tarakimu zote kwa haki ya tarakimu inayozunguka.
Angalia kwamba tarakimu zilizofutwa hazikubadilishwa na zero.

ⓑ kwa kumi ya karibu

Pata sehemu ya kumi na mshale.
Weka tarakimu kwa haki ya thamani ya mahali.
Kwa sababu 7 ni kubwa kuliko au sawa na 5, kuongeza 1 kwa 3.
Andika upya nambari, uondoe tarakimu zote kwa haki ya tarakimu inayozunguka.
Angalia kwamba tarakimu zilizofutwa hazikubadilishwa na zero.

ⓒ kwa nambari nzima iliyo karibu

Machapisho mahali wale na mshale.
Weka tarakimu kwa haki ya thamani ya mahali.
Tangu 3 si kubwa kuliko au sawa na 5, usiongeze 1 kwa 8.
Andika upya nambari, uondoe tarakimu zote kwa haki ya tarakimu inayozunguka.

MFANO\(\PageIndex{2}\)

\(6.582\)Pande zote kwa karibu ⓐ mia ⓑ kumi ⓒ idadi nzima.

Jibu

ⓐ\(6.58\) ⓑ\(6.6\) ⓒ\(7\)

MFANO\(\PageIndex{3}\)

\(15.2175\)Pande zote kwa karibu ⓐ elfu ⓑ mia ⓒ kumi.

Jibu

ⓐ\(15.218\) ⓑ\(15.22\)

ⓒ\(15.2\)

Kuongeza na Ondoa Decimals

Ili kuongeza au kuondoa decimals, tunasimamia pointi za decimal. Kwa kuunganisha pointi za decimal kwa njia hii, tunaweza kuongeza au kuondoa maadili ya mahali yanayofanana. Sisi kisha kuongeza au Ondoa idadi kama walikuwa idadi nzima na kisha mahali uhakika decimal katika jumla.

ONGEZA AU ONDOA DECIMALS.

1. Kuamua ishara ya jumla au tofauti.
2. Andika namba ili pointi decimal line up wima.
3. Tumia zero kama mahali placeholders, kama inahitajika.
4. Ongeza au uondoe namba kama zilikuwa namba nzima. Kisha weka hatua ya
   decimal katika jibu chini ya pointi za decimal katika namba zilizotolewa.
5. Andika jumla au tofauti na ishara sahihi.

MFANO\(\PageIndex{4}\)

Kuongeza au Ondoa: ⓐ\(−23.5−41.38\) ⓑ\(14.65−20.\)

Jibu

ⓐ

\(\begin{array}{ll} \text{} & −23.5−41.38 \\ \\ \\ {\text{The difference will be negative. To subtract, we add the} \\ \text{numerals. Write the numbers so the decimal points line} \\ \text{up vertically.}} & { \; \; 23.5 \\ \underline{+41.38}} \\ \\ \\ { \text{Put 0 as a placeholder after the 5 in 23.5.} \\ \text{Remember, } \frac{5}{10}=\frac{50}{100} \text{ so } 0.5=0.50.} & { \; \; 23.50 \\ \underline{+41.38}} \\ \\ \\ {\text{Add the numbers as if they were whole numbers.} \\ \text{Then place the decimal point in the sum.}} & {\; \; 23.50 \\ \underline{+41.38} \\ \; \; 64.88 } \\ \\ \\ \text{ Write the result with the correct sign.} & 64.88−23.5−41.38=−64.88 \end{array}\)

ⓑ

\(\begin{array}{ll} \text{} & 14.65−20 \\ \\ \\ {\text{The difference will be negative. To subtract, we} \\ \text{subtract 14.65 from 20.}} \\ \\ \\ {\text{Write the numbers so the decimal points line up} \\ \text{vertically.}} & { \; \; 20 \\ \underline{−14.65}} \\ \\ \\ {\text{Remember, 20 is a whole number, so place the} \\ \text{decimal point after the 0.}} \\ \\ \\ \text{Put in zeros to the right as placeholders.} & { \; \; 20.00 \\ \underline{−14.65}} \\ \\ \\ \text{Subtract and place the decimal point in the answer.} & {\begin{array}{lcccc} {} & 9 & {} & 9 & {} \\ 1 & \cancel{10} & {} & \cancel{10} & 10 \\ 2 & 0 & . & 0 & 0 \\ −1 & 4 & . & 6 & 5 \end{array} \\ \text{______________________} \\ \begin{array}{lcccc} {\; \; \; \; \; \; \; \; \; } & 5 & . & 3 & 5 \end{array}} \\ \\ \\ \text{Write the result with the correct sign.} & 14.65−20=−5.35 \end{array} \)

MFANO\(\PageIndex{5}\)

Kuongeza au Ondoa: ⓐ\(−4.8−11.69\) ⓑ\(9.58−10\).

Jibu

ⓐ\(−16.49\) ⓑ\(−0.42\)

MFANO\(\PageIndex{6}\)

Kuongeza au Ondoa: ⓐ\(−5.123−18.47\) ⓑ\(37.42−50\).

Jibu

ⓐ\(−23.593\) ⓑ\(−12.58\)

Kuzidisha na Gawanya Decimals

Tunapozidisha decimals zilizosainiwa, kwanza tunaamua ishara ya bidhaa na kisha kuzidisha kama namba zilikuwa chanya. Sisi kuzidisha idadi kwa muda kupuuza uhakika decimal na kisha kuhesabu idadi ya pointi decimal katika mambo na kwamba jumla inatuambia idadi ya maeneo decimal katika bidhaa. Hatimaye, tunaandika bidhaa kwa ishara sahihi.

KUZIDISHA DESIMALS.

1. Tambua ishara ya bidhaa.
2. Andika katika muundo wa wima, ukiweka namba upande wa kulia. Panua nambari kama zilikuwa namba nzima, kwa muda kupuuza pointi za decimal.
3. Weka hatua ya decimal. Idadi ya maeneo ya decimal katika bidhaa ni jumla ya idadi
   ya maeneo ya decimal katika mambo.
4. Andika bidhaa na ishara sahihi.

Kuzidisha:\((−3.9)(4.075)\).

Jibu

	\((−3.9)(4.075)\)
Ishara ni tofauti. Bidhaa itakuwa hasi.	Bidhaa itakuwa hasi.
Andika katika muundo wa wima, ukiweka namba upande wa kulia.
Kuzidisha.
Ongeza idadi ya maeneo ya decimal katika mambo (1 + 3). Weka sehemu ya decimal 4 maeneo kutoka kulia.
Ishara ni tofauti, hivyo bidhaa ni hasi.	\((−3.9)(4.075)=−15.8925\)

Kuzidisha:\(−4.5(6.107)\).

Jibu

\(−27.4815\)

MFANO\(\PageIndex{9}\)

Kuzidisha:\(−10.79(8.12)\).

Jibu

\(−87.6148\)

Mara nyingi, hasa katika sayansi, utazidisha decimals kwa nguvu za 10 (10, 100, 1000, nk). Ikiwa unazidisha bidhaa chache kwenye karatasi, unaweza kuona mfano unaohusiana na idadi ya zero katika nguvu ya 10 hadi idadi ya maeneo ya decimal tunahamisha hatua ya decimal kwa haki ya kupata bidhaa.

PANUA DECIMAL KWA NGUVU YA KUMI.

1. Hoja hatua ya decimal kwa haki idadi sawa ya maeneo kama
   idadi ya zero katika nguvu ya 10.
2. Ongeza zero mwishoni mwa nambari kama inahitajika.

MFANO\(\PageIndex{10}\)

Kuzidisha: 5.63 na ⓐ 10 ⓑ 100 ⓒ 1000.

Jibu

Kwa kuangalia idadi ya zeros katika nyingi ya kumi, tunaona idadi ya maeneo tunahitaji hoja decimal na haki.

ⓐ

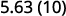
Kuna 1 sifuri katika 10, hivyo hoja decimal uhakika 1 mahali pa kulia.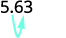

ⓑ

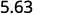
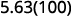
Kuna zero 2 katika 100, hivyo songa sehemu ya decimal 2 kwa haki.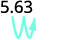

ⓒ

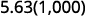
Kuna zeroes 3 katika 1,000, hivyo hoja decimal uhakika 3 mahali na haki.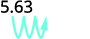
Zero lazima iongezwe hadi mwisho.

MFANO\(\PageIndex{11}\)

Kuzidisha 2.58 na ⓐ 10 ⓑ 100 ⓒ 1000.

Jibu

ⓐ 25.8 ⓑ 258 ⓒ 2,580

MFANO\(\PageIndex{12}\)

Panua 14.2 na ⓐ 10 ⓑ 100 ⓒ 1000.

Jibu

ⓐ 142 ⓑ 1,420 ⓒ 14,200

Kama ilivyo kwa kuzidisha, mgawanyiko wa decimals zilizosainiwa ni sawa na kugawa namba nzima. Tunapaswa tu kujua ambapo hatua ya decimal inapaswa kuwekwa na ishara ya quotient. Unapogawanya decimals zilizosainiwa, kwanza onyesha ishara ya quotient na kisha ugawanye kama namba zilikuwa chanya. Hatimaye, andika quotient na ishara sahihi.

Tunaangalia maelezo na msamiati wa mgawanyiko:

Tutaandika hatua za kuchukua wakati wa kugawa decimals kwa kumbukumbu rahisi.

GAWANYA DESICIMALS.

1. Tambua ishara ya quotient.
2. Fanya mgawanyiko namba nzima kwa “kusonga” hatua ya decimal njia yote ya kulia. “Hoja” hatua decimal katika mgao idadi sawa ya maeneo-kuongeza zero kama inahitajika.
3. Gawanya. Weka alama ya decimal katika quotient juu ya hatua ya decimal katika mgao.
4. Andika quotient na ishara sahihi.

MFANO\(\PageIndex{13}\)

Gawanya:\(−25.65÷(−0.06)\).

Jibu

Kumbuka, unaweza “hoja” decimals katika mgawanyiko na mgao kwa sababu ya sawa FRACTIONS Mali.

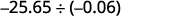
Ishara ni sawa.	Quotient ni chanya.
Fanya mgawanyiko namba nzima kwa “kusonga” hatua ya decimal njia yote ya kulia.
“Hoja” hatua decimal katika mgao idadi sawa ya maeneo.
Gawanya. Weka alama ya decimal katika quotient juu ya hatua ya decimal katika mgao.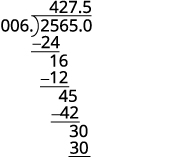
Andika quotient na ishara sahihi.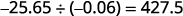

MFANO\(\PageIndex{14}\)

Gawanya:\(−23.492÷(−0.04)\).

Jibu

\(587.3\)

MFANO\(\PageIndex{15}\)

Gawanya:\(−4.11÷(−0.12)\).

Jibu

\(34.25\)

Badilisha Decimals, Fractions, na asilimia

Katika kazi yetu, mara nyingi ni muhimu kubadili fomu ya namba. Tunaweza kuwa na mabadiliko ya sehemu decimals au decimals kwa asilimia.

Tunabadilisha decimals katika sehemu ndogo kwa kutambua thamani ya mahali ya tarakimu ya mwisho (mbali kabisa). Katika decimal 0.03. 3 iko katika sehemu ya hundredths, hivyo 100 ni denominator ya sehemu sawa na 0.03.

\[0.03=\dfrac{3}{100}\]

Hatua za kuchukua ili kubadilisha decimal kwa sehemu zinafupishwa katika sanduku la utaratibu.

BADILISHA DECIMAL KWA SEHEMU SAHIHI NA SEHEMU KWA DECIMAL.

1. Ili kubadilisha decimal kwa sehemu sahihi, tambua thamani ya mahali ya tarakimu ya mwisho.
2. Andika sehemu.
   • nambari - “nambari” kwa haki ya hatua ya decimal
   • denominator-thamani mahali sambamba na tarakimu ya mwisho
3. Ili kubadilisha sehemu kwa decimal, ugawanye nambari ya sehemu na denominator ya sehemu.

MFANO\(\PageIndex{16}\)

Andika: ⓐ\(0.374\) kama sehemu ⓑ\(−\frac{5}{8}\) kama decimal.

Jibu

ⓐ

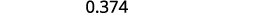
Tambua thamani ya mahali ya tarakimu ya mwisho.
Andika sehemu ya 0.374: Nambari ni 374. Denominator ni 1,000.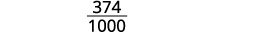
Kurahisisha sehemu.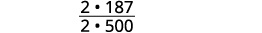
Gawanya mambo ya kawaida.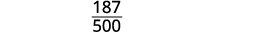

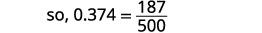
ⓑ Tangu sehemu bar ina maana mgawanyiko, sisi kuanza kwa kuandika sehemu\(\frac{5}{8}\) kama\(8\sqrt{5}\). Sasa ugawanye.

MFANO\(\PageIndex{17}\)

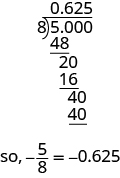
Andika: ⓐ\(0.234\) kama sehemu ⓑ\(−\frac{7}{8}\) kama decimal.

Jibu

ⓐ\(\frac{117}{500}\) ⓑ\(−0.875\)

MFANO\(\PageIndex{18}\)

Andika: ⓐ\(0.024\) kama sehemu ⓑ\(−\frac{3}{8}\) kama decimal.

Jibu

ⓐ\(\frac{3}{125}\) ⓑ\(−0.375\)

Asilimia ni uwiano ambao denominator yake ni 100. Asilimia ina maana kwa mia moja. Tunatumia alama ya asilimia,%, ili kuonyesha asilimia. Kwa kuwa asilimia ni uwiano, inaweza kuelezwa kwa urahisi kama sehemu. Asilimia ina maana kwa 100, hivyo denominator ya sehemu ni 100. Sisi kisha kubadilisha sehemu kwa decimal kwa kugawanya nambari na denominator. Baada ya kufanya hivyo mara nyingi, unaweza kuona mfano.

Ili kubadilisha idadi ya asilimia kwa idadi ya decimal, tunahamisha sehemu ya decimal mbili upande wa kushoto.

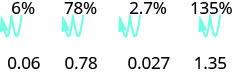
Ili kubadilisha decimal kwa asilimia, kumbuka kwamba asilimia ina maana kwa mia moja. Ikiwa tunabadilisha decimal kuwa sehemu ambayo denominator ni 100, ni rahisi kubadili sehemu hiyo kwa asilimia. Baada ya mabadiliko mengi, unaweza kutambua ruwaza.

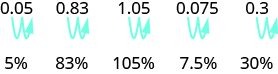
Kubadili decimal kwa asilimia, sisi hoja decimal uhakika maeneo mawili na haki na kisha kuongeza asilimia ishara.

BADILISHA ASILIMIA KWA DECIMAL NA DECIMAL KWA ASILIMIA.

1. Ili kubadilisha asilimia kwa decimal, songa sehemu ya decimal sehemu mbili upande wa kushoto baada ya kuondoa ishara ya asilimia.
2. Kubadili decimal kwa asilimia, hoja decimal uhakika sehemu mbili kwa haki na kisha kuongeza asilimia ishara.

MFANO\(\PageIndex{19}\)

Badilisha kila mmoja:

ⓐ asilimia kwa decimal: 62%, 135%, na 13.7%.

ⓑ decimal kwa asilimia: 0.51, 1.25, na 0.093.

Jibu

ⓐ

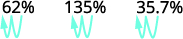
Hoja alama ya decimal sehemu mbili upande wa kushoto.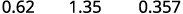

ⓑ

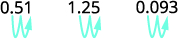
Hoja alama ya decimal sehemu mbili kwa haki.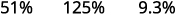

MFANO\(\PageIndex{20}\)

Badilisha kila mmoja:

ⓐ asilimia kwa decimal: 9%, 87%, na 3.9%.

ⓑ decimal kwa asilimia: 0.17, 1.75, na 0.0825.

Jibu

ⓐ 0.09, 0.87, 0.039 ⓑ 17%, 175%, 8.25%

MFANO\(\PageIndex{21}\)

Badilisha kila mmoja:

ⓐ asilimia kwa decimal: 3%, 91%, na 8.3%.

ⓑ decimal kwa asilimia: 0.41, 2.25, na 0.0925.

Jibu

ⓐ 0.03, 0.91, 0.083 ⓑ 41%, 225%, 9.25%

Rahisisha maneno na Mizizi ya Mraba

Kumbuka kwamba wakati idadi\(n\) imeongezeka kwa yenyewe, tunaandika\(n^2\) na kuisoma “\(n\)mraba.” Matokeo huitwa mraba wa nambari n. Kwa mfano,\(\frac{8}{2}\) inasoma “8 squared” na 64 inaitwa mraba wa 8. Vilevile, 121 ni mraba wa 11 kwa sababu\(11^2\) ni 121. Itakuwa na manufaa kujifunza kutambua namba kamili za mraba.

MRABA WA IDADI

Ikiwa\(n^2=m\), basi m ni mraba wa n.

Nini kuhusu mraba wa idadi hasi? Tunajua kwamba wakati ishara za namba mbili ni sawa, bidhaa zao ni chanya. Hivyo mraba wa idadi yoyote hasi pia ni chanya.

\[(−3)^2=9 \; \; \; \; \; \; \; \; \; (−8)^2=64 \; \; \; \; \; \; \; \; \; (−11)^2=121 \; \; \; \; \; \; \; \; \; (−15)^2=225\]

Kwa sababu\(10^2=100\), tunasema 100 ni mraba wa 10. Tunasema pia kwamba 10 ni mizizi ya mraba ya 100. Nambari ambayo mraba ni m inaitwa mizizi ya mraba ya namba m.

MIZIZI YA MRABA YA IDADI

Ikiwa\(n^2=m\), basi n ni mizizi ya mraba ya m.

Angalia\((−10)^2=100\) pia, hivyo -10 pia ni mzizi wa mraba wa 100. Kwa hiyo, wote 10 na -10 ni mizizi ya mraba ya 100. Kwa hiyo, kila idadi nzuri ina mizizi miwili ya mraba-moja chanya na moja hasi. Ishara kubwa\(\sqrt{m}\), inaashiria mizizi nzuri ya mraba. Mizizi nzuri ya mraba inaitwa mizizi kuu ya mraba. Tunapotumia ishara kali ambayo daima inamaanisha tunataka mizizi kuu ya mraba.

MRABA MIZIZI NOTATION

\(\sqrt{m}\)inasoma “mizizi ya mraba ya mm.”

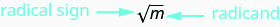
Ikiwa\(m=n^2\), basi\(\sqrt{m}=n\), kwa\(n≥0\).

Mzizi wa mraba wa m\(\sqrt{m}\),, ni idadi nzuri ambayo mraba ni m.

Tunajua kwamba kila nambari nzuri ina mizizi miwili ya mraba na ishara kubwa inaonyesha moja nzuri. Tunaandika\(\sqrt{100}=10\). Ikiwa tunataka kupata mizizi ya mraba hasi ya nambari, tunaweka hasi mbele ya ishara kubwa. Kwa mfano,\(−\sqrt{100}=−10\). Tunasoma\(−\sqrt{100}\) kama “kinyume cha mizizi kuu ya mraba ya 10.”

Zoezi\(\PageIndex{22}\)

Kurahisisha: ⓐ\(\sqrt{25}\) ⓑ\(\sqrt{121}\) ⓒ\(−\sqrt{144}\).

Jibu

ⓐ

\(\begin{array}{ll} \text{} & \sqrt{25} \\ \text{Since }5^2=25 & 5 \end{array}\)

ⓑ

\(\begin{array}{ll} \text{} & \sqrt{121} \\ \text{Since }11^2=121 & 11 \end{array}\)

ⓒ

\(\begin{array}{ll} {} & −\sqrt{144} \\ \text{The negative is in front of} & −12 \\ \text{the radical sign.} \end{array}\)

Zoezi\(\PageIndex{23}\)

Kurahisisha: ⓐ\(\sqrt{36}\) ⓑ\(\sqrt{169}\) ⓒ\(−\sqrt{225}\)

Jibu

ⓐ 6 ⓑ 13 ⓒ -15

Zoezi\(\PageIndex{24}\)

Kurahisisha: ⓐ\(\sqrt{16}\) ⓑ\(\sqrt{196}\) ⓒ\(−\sqrt{100}\)

Jibu

ⓐ 4 ⓑ 14 ⓒ -10

Tambua Integers, Nambari za busara, Hesabu zisizofaa, na Hesabu halisi

Sisi tayari ilivyoelezwa idadi kama kuhesabu s idadi, idadi nzima s, na integers. Ni tofauti gani kati ya aina hizi za namba? Tofauti inaweza kuchanganyikiwa na kuondoa. Vipi kuhusu kuuliza jinsi tunavyofautisha kati ya aina hizi za namba?

\[\begin{array}{ll} \text{Counting numbers} & 1,2,3,4,….. \\ \text{Whole numbers} & 0,1,2,3,4,…. \\ \text{Integers} & ….−3,−2,−1,0,1,2,3,…. \end{array}\]

Ni aina gani ya idadi bila sisi kupata kama sisi ilianza na integers wote na kisha ni pamoja na FRACTIONS wote? Nambari ambazo tungependa kuunda seti ya namba za busara. Nambari ya busara ni namba ambayo inaweza kuandikwa kama uwiano wa integers mbili.

Kwa ujumla, decimal yoyote inayoishia baada ya tarakimu kadhaa (kama vile 7.3 au -1.2684) ni namba ya busara. Tunaweza kutumia thamani ya mahali ya tarakimu ya mwisho kama denominator wakati wa kuandika decimal kama sehemu. Nambari ya decimal\(\frac{1}{3}\) ni namba\(0.\overline{3}\). Bar juu ya 3 inaonyesha kwamba namba 3 inarudia sana. Kuendelea ina maana muhimu katika calculus. Nambari (s) chini ya bar inaitwa kuzuia kurudia na inarudia kuendelea.

Kwa kuwa integers zote zinaweza kuandikwa kama sehemu ambayo denominator ni 1, integers (na hivyo pia idadi ya kuhesabu na nzima. ni namba za busara.

Kila idadi ya busara inaweza kuandikwa wote kama uwiano wa integers\(\frac{p}{q}\), ambapo p na q ni integers na\(q≠0\), na kama decimal kwamba ataacha au kurudia.

IDADI YA BUSARA

Nambari ya busara ni idadi ya fomu\(\frac{p}{q}\), ambapo p na q ni integers na\(q≠0\).

Fomu yake ya decimal inacha au kurudia.

Je, kuna decimals yoyote ambayo haina kuacha au kurudia? Ndiyo! Nambari ππ (herufi ya Kigiriki pi, inayojulikana “pie”), ambayo ni muhimu sana katika kuelezea miduara, ina umbo la decimal isiyoacha wala kurudia. Tunatumia dots tatu (...) kuonyesha decimal haina kuacha au kurudia.

\[π=3.141592654...\]

Mzizi wa mraba wa namba ambayo si mraba kamilifu ni decimal ambayo haina kuacha au kurudia.

Nambari ambazo fomu ya decimal haina kuacha au kurudia haiwezi kuandikwa kama sehemu ya integers. Tunaita hii namba isiyo ya maana.

NAMBARI ISIYO NA MAANA

Nambari isiyo na maana ni namba ambayo haiwezi kuandikwa kama uwiano wa integers mbili.

Fomu yake ya decimal haina kuacha na haina kurudia.

Hebu tufanye muhtasari njia tunayoweza kutumia ili kuamua kama namba ni ya busara au isiyo ya maana.

BUSARA AU ISIYO NA MAANA

Kama fomu decimal ya idadi

• kurudia au ataacha, idadi ni idadi ya busara.
• haina kurudia na haina kuacha, idadi ni idadi irrational.

Tumeona kwamba namba zote za kuhesabu ni namba nzima, namba zote ni integers, na integers zote ni namba za busara. Nambari zisizo na maana ni namba ambazo fomu ya decimal haina kuacha na haina kurudia. Wakati sisi kuweka pamoja idadi ya busara na idadi irrational, sisi kupata seti ya idadi halisi s.

NAMBARI HALISI

Nambari halisi ni namba ambayo ni ya busara au isiyo ya maana.

Baadaye katika kozi hii tutaanzisha namba zaidi ya idadi halisi. Kielelezo unaeleza jinsi seti idadi tumekuwa kutumika hadi sasa fit pamoja.

Kielelezo 2. Chati hii inaonyesha seti za namba zinazounda seti ya namba halisi.

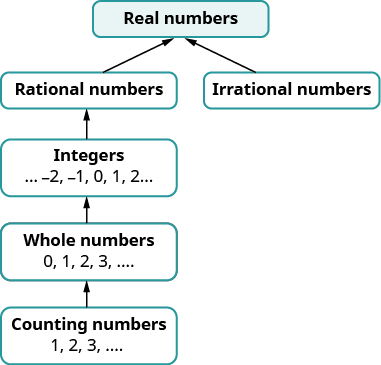
Je! Neno “namba halisi” linaonekana kuwa la ajabu kwako? Je, kuna idadi yoyote ambayo si “halisi,” na, ikiwa ni hivyo, inaweza kuwa nini? Je, tunaweza kurahisisha\(−\sqrt{25}\)? Je, kuna idadi ambayo mraba ni\(−25\)?

\[()^2=−25?\]

Hakuna hata idadi kwamba sisi kushughulikiwa na hadi sasa ina mraba yaani\(−25\). Kwa nini? Nambari yoyote nzuri ya mraba ni chanya. Nambari yoyote mbaya ya mraba ni chanya. Kwa hiyo tunasema hakuna idadi halisi sawa na\(\sqrt{−25}\). Mzizi wa mraba wa nambari hasi sio namba halisi.

Zoezi\(\PageIndex{25}\)

Kutokana na idadi\(−7,\frac{14}{5},8,\sqrt{5},5.9,−\sqrt{64}\), orodha ⓐ namba nzima ⓑ integers ⓒ namba za busara ⓓ nambari zisizo na maana ⓔ namba halisi.

Jibu

ⓐ Kumbuka, namba nzima ni\(0,1,2,3,…,\) hivyo 8 ni namba nzima pekee iliyotolewa.

ⓑ integers ni idadi nzima na kinyume yao (ambayo ni pamoja na 0). Hivyo idadi nzima 8 ni integer, na -7 ni kinyume cha idadi nzima hivyo ni integer, pia. Pia, angalia kwamba 64 ni mraba wa 8 hivyo\(−\sqrt{64}=−8\). Hivyo integers ni\(−7,8,\) na\(−\sqrt{64}\).

ⓒ Kwa kuwa integers zote ni busara, basi\(−7,8,\) na\(−\sqrt{64}\) ni busara. Nambari za busara pia zinajumuisha sehemu ndogo na decimals ambazo hurudia au kuacha, hivyo\(\frac{14}{5}\) na\(5.9\) ni busara. Hivyo orodha ya namba za busara ni\(−7,\frac{14}{5},8,5.9,\) na\(−\sqrt{64}\).

ⓓ Kumbuka kwamba 5 si mraba kamili, hivyo\(\sqrt{5}\) ni irrational.

ⓔ Nambari zote zilizoorodheshwa ni namba halisi.

Zoezi\(\PageIndex{26}\)

Kutokana na idadi\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49},\) orodha ⓐ namba nzima ⓑ integers ⓒ namba za busara

ⓓ namba irrational ⓔ namba halisi.

Jibu

ⓐ\(4,\sqrt{49}\) ⓑ\(−3,4,\sqrt{49}\)

ⓒ\(−3,0.\overline{3},\frac{9}{5},4,\sqrt{49}\) ⓓ\(−\sqrt{2}\)

ⓔ\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49}\)

Zoezi\(\PageIndex{27}\)

Idadi kutokana na\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...,\) orodha ⓐ namba nzima ⓑ integers ⓒ namba busara ⓓ namba irrational ⓔ namba halisi.

Jibu

ⓐ\(6,\sqrt{121}\)

ⓑ\(−\sqrt{25},−1,6,\sqrt{121}\)

ⓒ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121}\)

ⓓ\(2.041975...\)

ⓔ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...\)

Pata sehemu ndogo na Decimals kwenye Mstari wa Idadi

Sasa tunataka kuingiza sehemu ndogo na decimals kwenye mstari wa namba. Hebu tuanze na sehemu ndogo na upate\(\frac{1}{5},−\frac{4}{5},3,\frac{7}{4},−\frac{9}{2},−5\) na\(\frac{8}{3}\) kwenye mstari wa nambari.

Tutaanza na namba nzima 3 na -5 kwa sababu ni rahisi kupanga njama. Angalia Kielelezo.

FRACTIONS sahihi waliotajwa ni\(\frac{1}{5}\) na\(−\frac{4}{5}.\) Tunajua sehemu sahihi\(\frac{1}{5}\) ina thamani chini ya moja na hivyo itakuwa iko kati ya 0 na 1. Denominator ni 5, kwa hiyo tunagawanya kitengo kutoka 0 hadi 1 hadi sehemu 5 sawa\(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\). Sisi njama\(\frac{1}{5}\).

Vilevile,\(−\frac{4}{5}\) iko kati ya 0 na -1. Baada ya kugawanya kitengo katika sehemu 5 sawa tunapanga njama\(−\frac{4}{5}\).

Hatimaye, angalia sehemu zisizofaa\(\frac{7}{4},\frac{9}{2},\frac{8}{3}\). Kuweka pointi hizi inaweza kuwa rahisi ikiwa utabadilisha kila mmoja kwa namba iliyochanganywa.

\[\dfrac{7}{4}=1\dfrac{3}{4} \; \; \; \; \; \; \; \; \; −\dfrac{9}{2}=−4\dfrac{1}{2} \; \; \; \; \; \; \; \; \; \dfrac{8}{3}=2\dfrac{2}{3}\]

Kielelezo kinaonyesha mstari wa nambari na pointi zote zilizopangwa.

Zoezi\(\PageIndex{28}\)

Machapisho na studio yafuatayo kwenye mstari namba:\(4,\frac{3}{4},−\frac{1}{4},−3,\frac{6}{5},−\frac{5}{2},\) na\(\frac{7}{3}\).

Jibu

Machapisho na njama integers,\(4,−3.\)

Pata sehemu sahihi\(\frac{3}{4}\) kwanza. Sehemu\(\frac{3}{4}\) ni kati ya 0 na 1. Gawanya umbali kati ya 0 na 1 katika sehemu nne sawa, basi tunapanga njama\(\frac{3}{4}\). Vile vile njama\(−\frac{1}{4}\).

Sasa Pata sehemu zisizofaa\(\frac{6}{5},−\frac{5}{2},\) na\(\frac{7}{3}\). Ni rahisi kuwapanga njama ikiwa tunawabadilisha kwa idadi iliyochanganywa na kisha uwapange kama ilivyoelezwa hapo juu:\(\frac{6}{5}=1\frac{1}{5},−\frac{5}{2}=−2\frac{1}{2},\frac{7}{3}=2\frac{1}{3}\).

Zoezi\(\PageIndex{29}\)

Machapisho na lebo zifuatazo kwenye mstari namba:\(−1,\frac{1}{3},\frac{6}{5},−\frac{7}{4},\frac{9}{2},5,−\frac{8}{3}\).

Jibu

Zoezi\(\PageIndex{30}\)

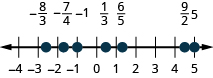
Machapisho na lebo zifuatazo kwenye mstari namba:\(−2,\frac{2}{3},\frac{7}{5},−\frac{7}{4},\frac{7}{2},3,−\frac{7}{3}\).

Jibu

Zoezi\(\PageIndex{31}\)

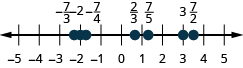
Kwa kuwa decimals ni aina ya sehemu ndogo, kupata decimals kwenye mstari wa nambari ni sawa na kupata sehemu ndogo kwenye mstari wa namba.

Pata kwenye mstari wa nambari: ⓐ 0.4 ⓑ -0.74.

Jibu

ⓐ Nambari ya decimal 0.4 ni sawa na, sehemu sahihi, hivyo 0.4 iko kati ya 0 na 1.\(\frac{4}{10}\) Kwenye mstari wa nambari, fungua muda kati ya 0 na 1 hadi sehemu 10 sawa. Sasa lebo sehemu 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0. Tunaandika 0 kama 0.0 na 1 kama 1.0, ili idadi ni mara kwa mara katika sehemu ya kumi. Hatimaye, alama 0.4 kwenye mstari wa nambari.

ⓑ Decimal\(−0.74\) ni sawa na\(−\frac{74}{100}\), hivyo iko kati ya 0 na .-1. Kwenye mstari wa nambari, alama na uandike alama ya hundredths katika muda kati ya 0 na -1.

Zoezi\(\PageIndex{32}\)

Machapisho kwenye mstari namba: ⓐ\(0.6\) ⓑ\(−0.25.\)

Jibu

ⓐ

ⓑ

Zoezi\(\PageIndex{33}\)

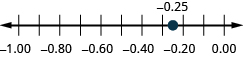
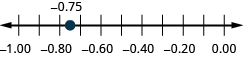
Pata kwenye mstari wa namba: ⓐ 0.90.9 ⓑ -0.75.-0.75.

Jibu

ⓐ

ⓑ

Kupata rasilimali hii online kwa maelekezo ya ziada na mazoezi na decimals.

• Misingi ya Hesabu: Kugawanya Decimals

Dhana muhimu

• Jinsi ya kuzunguka decimals.
  1. Pata thamani ya mahali uliyopewa na uiangalie kwa mshale.
  2. Weka tarakimu kwa haki ya thamani ya mahali.
  3. Je, tarakimu iliyopigwa mstari ni kubwa kuliko au sawa na 5?
     • Ndiyo: ongeza 1 kwa tarakimu katika thamani ya mahali uliyopewa.
     • Hapana: usibadili tarakimu katika thamani ya mahali uliyopewa
  4. Andika upya nambari, uondoe tarakimu zote kwa haki ya tarakimu inayozunguka.
• Jinsi ya kuongeza au kuondoa decimals.
  1. Kuamua ishara ya jumla au tofauti.
  2. Andika namba ili pointi decimal line up wima.
  3. Tumia zero kama mahali placeholders, kama inahitajika.
  4. Ongeza au uondoe namba kama zilikuwa namba nzima. Kisha weka hatua ya decimal katika jibu chini ya pointi za decimal katika namba zilizotolewa.
  5. Andika jumla au tofauti na ishara sahihi
• Jinsi ya kuzidisha decimals.
  1. Tambua ishara ya bidhaa.
  2. Andika katika muundo wa wima, ukiweka namba upande wa kulia. Panua nambari kama zilikuwa namba nzima, kwa muda kupuuza pointi za decimal.
  3. Weka hatua ya decimal. Idadi ya maeneo ya decimal katika bidhaa ni jumla ya idadi ya maeneo ya decimal katika mambo.
  4. Andika bidhaa na ishara sahihi.
• Jinsi ya kuzidisha decimal kwa nguvu ya kumi.
  1. Hoja hatua ya decimal kwa haki idadi sawa ya maeneo kama idadi ya zero katika nguvu ya 10.
  2. Ongeza zero mwishoni mwa nambari kama inahitajika.
• Jinsi ya kugawanya decimals.
  1. Tambua ishara ya quotient.
  2. Fanya mgawanyiko namba nzima kwa “kusonga” hatua ya decimal njia yote ya kulia. “Hoja” hatua decimal katika mgao idadi sawa ya maeneo-kuongeza zero kama inahitajika.
  3. Gawanya. Weka alama ya decimal katika quotient juu ya hatua ya decimal katika mgao.
  4. Andika quotient na ishara sahihi.
• Jinsi ya kubadilisha decimal kwa sehemu sahihi na sehemu kwa decimal.
  1. Ili kubadilisha decimal kwa sehemu sahihi, tambua thamani ya mahali ya tarakimu ya mwisho.
  2. Andika sehemu.
     • nambari - “nambari” kwa haki ya hatua ya decimal
     • denominator-thamani mahali sambamba na tarakimu ya mwisho
  3. Ili kubadilisha sehemu kwa decimal, ugawanye nambari ya sehemu na denominator ya sehemu.
• Jinsi ya kubadilisha asilimia kwa decimal na decimal kwa asilimia.
  1. Ili kubadilisha asilimia kwa decimal, songa sehemu ya decimal sehemu mbili upande wa kushoto baada ya kuondoa ishara ya asilimia.
  2. Kubadili decimal kwa asilimia, hoja decimal uhakika sehemu mbili kwa haki na kisha kuongeza asilimia ishara.
• Mizizi ya Mizizi ya Mraba\(\sqrt{m}\) inasoma “mizizi ya mraba ya m.” Ikiwa\(m=n^2\), basi\(\sqrt{m}=n\), kwa\(n≥0\). Mzizi wa mraba wa m\(\sqrt{m}\),, ni idadi nzuri ambayo mraba ni m.
• Mantiki au irrational Kama fomu decimal ya idadi
  • kurudia au ataacha, idadi ni idadi ya busara.
  • haina kurudia na haina kuacha, idadi ni idadi irrational.
• Hesabu halisi

  

  Kielelezo 4.

faharasa

idadi isiyo ya maana

Nambari isiyo na maana ni namba ambayo haiwezi kuandikwa kama uwiano wa integers mbili. Fomu yake ya decimal haina kuacha na haina kurudia.

asilimia

Asilimia ni uwiano ambao denominator yake ni 100.

mizizi kuu ya mraba

Mizizi nzuri ya mraba inaitwa mizizi kuu ya mraba.

idadi ya busara

Nambari ya busara ni idadi ya fomu\(\frac{p}{q}\), ambapo p na q ni integers na\(q≠0\). Fomu yake ya decimal inacha au kurudia.

nambari halisi

Nambari halisi ni namba ambayo ni ya busara au isiyo ya maana.

mraba wa idadi

Ikiwa\(n^2=m\), basi m ni mraba wa n.

mizizi ya mraba ya idadi

Ikiwa\(n^2=m\), basi n ni mizizi ya mraba ya m.