1.3: Nambari kamili
- Page ID
- 176112
Mwishoni mwa sehemu hii, utaweza:
- Kurahisisha maneno na thamani kamili
- Ongeza na uondoe integers
- Panua na ugawanye integers
- Kurahisisha maneno na integers
- Tathmini maneno ya kutofautiana na integers
- Tafsiri misemo kwa maneno na integers
- Tumia integers katika programu
Utangulizi wa kina zaidi wa mada yaliyofunikwa katika sehemu hii unaweza kupatikana katika sura ya Elementary Algebra, Misingi.
Kurahisisha Maneno na Thamani kamili
Nambari hasi ni namba chini ya 0. Nambari hasi ni upande wa kushoto wa sifuri kwenye mstari wa namba (Kielelezo\(\PageIndex{1}\)).
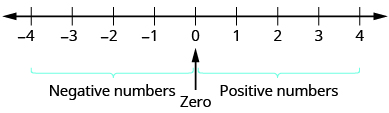
Kielelezo\(\PageIndex{1}\). Mstari wa nambari unaonyesha eneo la namba nzuri na hasi.
Huenda umeona kuwa, kwenye mstari wa nambari, namba hasi ni picha ya kioo ya namba nzuri, na sifuri katikati. Kwa sababu idadi\(2\) na\(−2\) ni umbali sawa kutoka sifuri, kila mmoja inaitwa kinyume cha nyingine. Kinyume cha\(2\) ni\(−2\), na kinyume cha\(−2\) ni\(2\).
Kinyume cha namba ni namba ambayo ni umbali sawa kutoka sifuri kwenye mstari wa namba lakini upande wa pili wa sifuri.
Kielelezo\(\PageIndex{2}\) unaeleza ufafanuzi.

Kielelezo\(\PageIndex{2}\). Kinyume cha 3 ni\(−3\).
\[\begin{align} & -a \text{ means the opposite of the number }a \\ & \text{The notation} -a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
Tuliona kwamba namba kama vile 3 na -3 ni kinyume kwa sababu zina umbali sawa kutoka 0 kwenye mstari wa namba. Wote wawili ni vitengo vitatu kutoka 0. Umbali kati ya 0 na namba yoyote kwenye mstari wa namba inaitwa thamani kamili ya namba hiyo.
Thamani kamili ya namba ni umbali wake kutoka 0 kwenye mstari wa namba.
Thamani kamili ya namba\(n\) imeandikwa kama\(|n|\) na\(|n|≥0\) kwa namba zote.
Maadili kamili daima ni makubwa kuliko au sawa na sifuri.
Kwa mfano,
\[\begin{align} & -5 \text{ is } 5 \text{ units away from 0, so } |-5|=5. \\ & 5 \text{ is }5\text{ units away from 0, so }|5|=5. \end{align}\]
Kielelezo\(\PageIndex{3}\) unaeleza wazo hili.
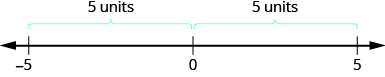
Thamani kamili ya namba haipatikani kamwe kwa sababu umbali hauwezi kuwa hasi. Nambari pekee yenye thamani kamili sawa na sifuri ni namba zero yenyewe kwa sababu umbali kutoka 0 hadi 0 kwenye mstari wa namba ni vitengo vya sifuri.
Katika mfano unaofuata, tutaweza ili maneno na maadili kamili.
Jaza\(<,\,>,\) au\(=\) kwa kila jozi zifuatazo za namba:
- \(\mathrm{|−5|}\_\_\mathrm{−|−5|}\_\_\mathrm{−|5|}\)
- \(\text{8__−|−8|}\)
- \(\text{−9__−|−9|}\)
- (\ maandishi {- (-16) __|16-16|}\).
- Jibu
-
a.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {|−5| \\ 5 \\ 5 \\ |−5|} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−5| \\ −5 \\ −5 \\ −|−5|} \end{array}\)
b.
\(\begin{array}{llcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {8 \\ 8 \\ 8 \\ 8} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−8| \\ −8 \\ −8 \\ −|−8|} \end{array}\)
c.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−9 \\ −9 \\ −9 \\ −9} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−9| \\ −9 \\ −9 \\ −|−9|} \end{array}\)
d.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−(−16) \\ 16 \\ 16 \\ −(−16)} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−16| \\ 16 \\ 16 \\ |−16|} \end{array}\)
Jaza\(<,\,>,\) au\(=\) kwa kila jozi zifuatazo za namba:
ⓐ\(−9 \_\_−|−9|\) ⓑ\(2 \_\_−|−2|\) ⓒ\(−8 \_\_|−8|\) ⓓ\(−(−9) \_\_|−9|.\)
- Jibu
-
ⓐ\(>\) ⓑ\(>\) ⓒ\(<\)
ⓓ\(=\)
Jaza\(<,>,\) au\(=\) kwa kila jozi zifuatazo za namba:
- \(7 \_\_ −|−7|\)
- \(−(−10) \_ \_|−10|\)
- \(|−4| \_\_ −|−4|\)
- \(−1 \_\_ |−1|.\)
- Jibu
-
ⓐ\(>\) ⓑ\(=\) ⓒ\(>\)
ⓓ\(<\)
Sasa tunaongeza baa za thamani kamili kwenye orodha yetu ya alama za makundi. Tunapotumia utaratibu wa shughuli, kwanza tunapunguza ndani ya baa za thamani kamili iwezekanavyo, basi tunachukua thamani kamili ya idadi inayosababisha.
\[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
Katika mfano unaofuata, sisi kurahisisha maneno ndani ya baa thamani kabisa kwanza tu kama sisi kufanya na mabano.
Kurahisisha:\(\mathrm{24−|19−3(6−2)|}\).
- Jibu
-
\(\begin{array}{lc} \text{} & 24−|19−3(6−2)| \\ \text{Work inside parentheses first:} & \text{} \\ \text{subtract 2 from 6.} & 24−|19−3(4)| \\ \text{Multiply 3(4).} & 24−|19−12| \\ \text{Subtract inside the absolute value bars.} & 24−|7| \\ \text{Take the absolute value.} & 24−7 \\ \text{Subtract.} & 17 \end{array}\)
Kurahisisha:\(19−|11−4(3−1)|\).
- Jibu
-
16
Kurahisisha:\(9−|8−4(7−5)|\).
- Jibu
-
9
Kuongeza na Ondoa Integers
Hadi sasa katika mifano yetu, tuna tu kutumika idadi kuhesabu na idadi nzima.
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3… \\ \text{Whole numbers} 0,1,2,3…. \end{array}\]
Kazi yetu na kupinga inatupa njia ya kufafanua integers. Nambari nzima na kupinga kwao huitwa integers. Integers ni idadi\(…−3,−2,−1,0,1,2,3…\)
Nambari nzima na kupinga kwao huitwa integers.
Integers ni idadi
\[…-3,-2,-1,0,1,2,3…,\]
Wanafunzi wengi ni vizuri na kuongeza na kutoa ukweli kwa idadi chanya. Lakini kufanya kuongeza au kuondoa kwa namba zote mbili nzuri na hasi inaweza kuwa changamoto zaidi.
Tutatumia counters mbili za rangi ili kuongezea mfano na uondoaji wa hasi ili uweze kutazama taratibu badala ya kukariri sheria.
Tunaruhusu rangi moja (bluu) inawakilisha chanya. Rangi nyingine (nyekundu) itawakilisha hasi.

Ikiwa tuna counter moja nzuri na counter moja hasi, thamani ya jozi ni sifuri. Wanaunda jozi ya neutral. Thamani ya jozi hii ya neutral ni sifuri.
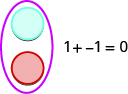
Tutatumia counters kuonyesha jinsi ya kuongeza:
\[5+3 \; \; \; \; \; \; −5+(−3) \; \; \; \; \; \; −5+3 \; \; \; \; \; \; \; 5+(−3)\]
Mfano wa kwanza,\(5+3,\) anaongeza 5 chanya na 3 chanya chanya.
Mfano wa pili,\(−5+(−3),\) anaongeza negatives 5 na 3 hasi - wote hasi.
Wakati ishara ni sawa, counters wote ni rangi sawa, na hivyo tunawaongeza. Katika kila kesi sisi kupata 8-ama 8 chanya au 8 hasi.

Kwa nini kinatokea wakati ishara ni tofauti? Hebu kuongeza\(−5+3\) na\(5+(−3)\).
Tunapotumia counters kwa mfano kuongeza ya integers chanya na hasi, ni rahisi kuona kama kuna counters chanya zaidi au zaidi hasi. Kwa hiyo tunajua kama jumla itakuwa chanya au hasi.
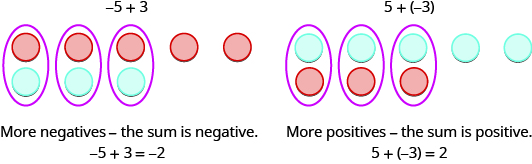
Kuongeza: ⓐ\(−1+(−4)\) ⓑ\(−1+5\) ⓒ\(1+(−5)\).
- Jibu
-
ⓐ
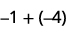

1 hasi pamoja na 4 hasi ni 5 hasi 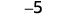
ⓑ
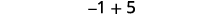

Kuna chanya zaidi, hivyo jumla ni chanya. 
ⓒ
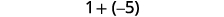

Kuna hasi zaidi, hivyo jumla ni hasi. 
Kuongeza: ⓐ\(−2+(−4)\) ⓑ\(−2+4\) ⓒ\(2+(−4)\).
- Jibu
-
ⓐ\(−6\) ⓑ\(2\) ⓒ\(−2\)
Kuongeza: ⓐ\(−2+(−5)\) ⓑ\(−2+5\) ⓒ\(2+(−5)\).
- Jibu
-
ⓐ\(−7\) ⓑ\(3\) ⓒ\(−3\)
Tutaendelea kutumia counters ili kutengeneza uondoaji. Labda ulipokuwa mdogo, unasoma\(“5−3”\) kama “5 uondoe 3.” Unapotumia counters, unaweza kufikiria kuondoa njia ile ile!
Tutatumia counters kuonyesha ili kuondoa:
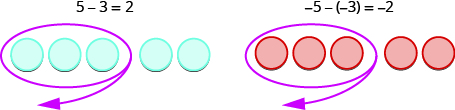
\[5−3 \; \; \; \; \; \; −5−(−3) \; \; \; \; \; \; −5−3 \; \; \; \; \; \; 5−(−3) \]
Mfano wa kwanza\(5−3\), tunaondoa chanya 3 kutoka kwa chanya cha 5 na kuishia na chanya 2.
Katika mfano wa pili,\(−5−(−3),\) tunaondoa hasi 3 kutoka kwa negatives 5 na kuishia na hasi 2.
Kila mfano ulitumia counters ya rangi moja tu, na mfano wa “kuchukua” wa kuondoa ulikuwa rahisi kutumia.
Ni nini kinachotokea wakati tunapaswa kuondoa namba moja nzuri na moja hasi? Tutahitaji kutumia counters zote za bluu na nyekundu pamoja na jozi zisizo na upande wowote. Kama hatuna idadi ya counters zinahitajika kuchukua, sisi kuongeza jozi neutral. Kuongeza jozi ya neutral haina mabadiliko ya thamani. Ni kama kubadilisha robo kwa nickels-thamani ni sawa, lakini inaonekana tofauti.
Hebu tuangalie\(−5−3\) na\(5−(−3)\).
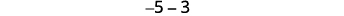 |
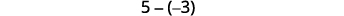 |
|
| Tengeneza nambari ya kwanza. |  |
 |
| Sasa tunaongeza jozi zinazohitajika za neutral. |  |
 |
| Tunaondoa idadi ya counters iliyowekwa na nambari ya pili. | 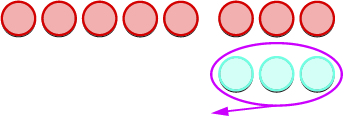 |
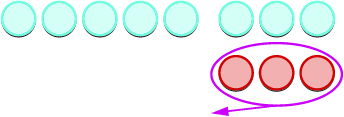 |
| Hesabu kile kilichoachwa. |  |
 |
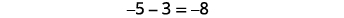 |
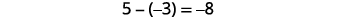 |
|
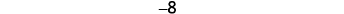 |
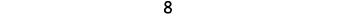 |
Ondoa: ⓐ\(3−1\) ⓑ\(−3−(−1)\) ⓒ\(−3−1\) ⓓ\(3−(−1)\).
- Jibu
-
ⓐ
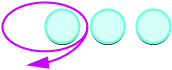
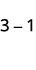
Chukua chanya 1 kutoka kwa chanya cha 3 na kupata chanya 2. 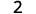
ⓑ

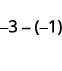
Chukua chanya 1 kutoka kwa hasi 3 na kupata hasi 2. 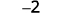
ⓒ

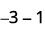
Chukua chanya 1 kutoka kwa jozi moja ya neutral iliyoongezwa. 
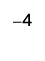
ⓓ

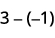
Chukua hasi 1 kutoka kwa jozi moja ya neutral iliyoongezwa. 

Ondoa: ⓐ\(6−4\) ⓑ\(−6−(−4)\) ⓒ\(−6−4\) ⓓ\(6−(−4)\).
- Jibu
-
ⓐ\(2\) ⓑ\(−2\) ⓒ\(−10\) ⓓ\(10\)
Ondoa: ⓐ\(7−4\) ⓑ\(−7−(−4)\) ⓒ\(−7−4\) ⓓ\(7−(−4)\).
- Jibu
-
ⓐ\(3\) ⓑ\(−3\) ⓒ\(−11\) ⓓ\(11\)
Je! Umeona kuwa uondoaji wa namba zilizosainiwa unaweza kufanywa kwa kuongeza kinyume? Katika mfano wa mwisho,\(−3−1\) ni sawa\(−3+(−1)\) na\(3−(−1)\) ni sawa na\(3+1\). Wewe mara nyingi kuona wazo hili, Ondoa Mali, imeandikwa kama ifuatavyo:
\[a−b=a+(−b)\]
Kuondoa namba ni sawa na kuongeza kinyume chake.
Kurahisisha: ⓐ\(13−8\)\(−17−9\) na\(13+(−8)\) ⓑ\(9−(−15)\) na\(−17+(−9)\) ⓒ na\(9+15\) ⓓ\(−7−(−4)\) na\(−7+4\).
- Jibu
-
ⓐ
\(\begin{array}{lccc} \text{} & 13−8 & \text{and} & 13+(−8) \\ \text{Subtract.} & 5 & \text{} & 5 \end{array}\)ⓑ
\(\begin{array}{lccc} \text{} & −17−9 & \text{and} & −17+(−9) \\ \text{Subtract.} & −26 & \text{} & −26 \end{array}\)
ⓒ
\(\begin{array}{lccc} \text{} & 9−(−15) & \text{and} & 9+15 \\ \text{Subtract.} & 24 & \text{} & 24 \end{array}\)
ⓓ
\(\begin{array}{lccc} \text{} & −7−(−4) & \text{and} & −7+4 \\ \text{Subtract.} & −3 & \text{} & −3 \end{array}\)
Kurahisisha: ⓐ\(21−13\)\(−11−7\) na\(21+(−13)\) ⓑ\(6−(−13)\) na\(−11+(−7)\) ⓒ na\(6+13\) ⓓ\(−5−(−1)\) na\(−5+1\).
- Jibu
-
ⓐ\(8,8\) ⓑ\(−18,−18\)
ⓒ\(19,19\) ⓓ\(−4,−4\)
Kurahisisha: ⓐ\(15−7\)\(−14−8\) na\(15+(−7)\) ⓑ\(4−(−19)\) na\(−14+(−8)\) ⓒ na\(4+19\) ⓓ\(−4−(−7)\) na\(−4+7\).
- Jibu
-
ⓐ\(8,8\) ⓑ\(−22,−22\)
ⓒ\(23,23\) ⓓ\(3,3\)
Nini kinatokea wakati kuna integers zaidi ya tatu? Tunatumia tu utaratibu wa shughuli kama kawaida.
Kurahisisha:\(7−(−4−3)−9.\)
- Jibu
-
\(\begin{array}{lc} \text{} & 7−(−4−3)−9 \\ \text{Simplify inside the parentheses first.} & 7−(−7)−9 \\ \text{Subtract left to right.} & 14−9 \\ \text{Subtract.} & 5 \end{array}\)
Kurahisisha:\(8−(−3−1)−9.\)
- Jibu
-
3
Kurahisisha:\(12−(−9−6)−14.\)
- Jibu
-
13
Kuzidisha na Gawanya Integers
Kwa kuwa kuzidisha ni shorthand ya hisabati kwa kuongeza mara kwa mara, mfano wetu unaweza kutumika kwa urahisi ili kuonyesha kuzidisha kwa integers. Hebu tuangalie mfano huu halisi ili uone ni mwelekeo gani tunaoona. Tutatumia mifano sawa ambayo tulitumia kwa kuongeza na kuondoa. Hapa, sisi ni kutumia mfano tu kutusaidia kugundua mfano.
Tunakumbuka kwamba aba·b ina maana kuongeza, mara b.
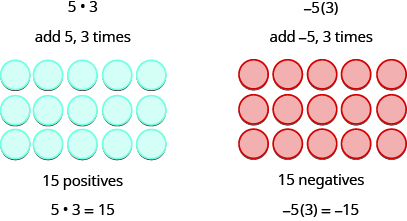
Mifano miwili ijayo ni ya kuvutia zaidi. Ina maana gani kuzidisha 5 na -3? Ina maana Ondoa mara 5,3. Kuangalia uondoaji kama “kuchukua”, inamaanisha kuchukua 5, mara 3. Lakini hakuna kitu cha kuchukua, kwa hiyo tunaanza kwa kuongeza jozi zisizo na upande kwenye nafasi ya kazi.
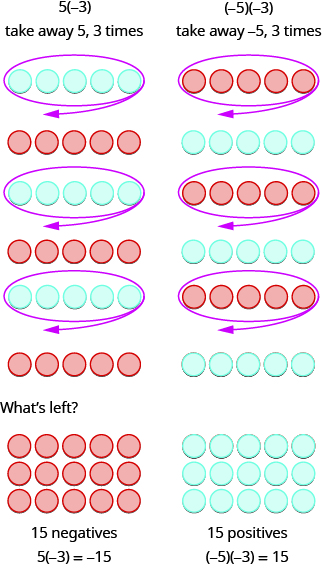
Kwa muhtasari:
\[\begin{array}{ll} 5·3=15 & −5(3)=−15 \\ 5(−3)=−15 & (−5)(−3)=15 \end{array}\]
Kumbuka kwamba kwa kuzidisha namba mbili zilizosainiwa, wakati
\[ \text{signs are the } \textbf{same} \text{, the product is } \textbf{positive.} \\ \text{signs are } \textbf{different} \text{, the product is } \textbf{negative.} \]
Nini kuhusu mgawanyiko? Idara ni operesheni inverse ya kuzidisha. Hivyo,\(15÷3=5\) kwa sababu\(15·3=15\). Kwa maneno, maneno haya yanasema kuwa 15 inaweza kugawanywa katika makundi 3 ya 5 kila mmoja kwa sababu kuongeza tano mara tatu inatoa 15. Ikiwa unatazama mifano fulani ya kuzidisha integers, unaweza kufikiri sheria za kugawa integers.
\[\begin{array}{lclrccl} 5·3=15 & \text{so} & 15÷3=5 & \text{ } −5(3)=−15 & \text{so} & −15÷3=−5 \\ (−5)(−3)=15 & \text{so} & 15÷(−3)=−5 & \text{ } 5(−3)=−15 & \text{so} & −15÷(−3)=5 \end{array}\]
Idara ifuatavyo sheria sawa na kuzidisha kuhusiana na ishara.
Kwa kuzidisha na mgawanyiko wa namba mbili zilizosainiwa:
| Ishara sawa | Matokeo |
|---|---|
| • Chanya mbili | Chanya |
| • Mbili hasi | Chanya |
Ikiwa ishara ni sawa, matokeo ni chanya.
| Ishara tofauti | Matokeo |
|---|---|
| • Chanya na hasi | Hasi |
| • Hasi na chanya | Hasi |
Ikiwa ishara ni tofauti, matokeo ni hasi.
Kuzidisha au kugawanya: ⓐ\(−100÷(−4)\) ⓑ\(7⋅6\) ⓒ\(4(−8)\) ⓓ\(−27÷3.\)
- Jibu
-
ⓐ
\(\begin{array}{lc} \text{} & −100÷(−4) \\ \text{Divide, with signs that are} \\ \text{the same the quotient is positive.} & 25 \end{array}\)
ⓑ
\(\begin{array} {lc} \text{} & 7·6 \\ \text{Multiply, with same signs.} & 42 \end{array}\)
ⓒ
\(\begin{array} {lc} \text{} & 4(−8) \\ \text{Multiply, with different signs.} & −32 \end{array}\)
ⓓ
\(\begin{array}{lc} \text{} & −27÷3 \\ \text{Divide, with different signs,} \\ \text{the quotient is negative.} & −9 \end{array}\)
Kuzidisha au kugawanya: ⓐ\(−115÷(−5)\) ⓑ\(5⋅12\) ⓒ\(9(−7)\) ⓓ\(−63÷7.\)
- Jibu
-
ⓐ 23 ⓑ 60 ⓒ -63 ⓓ -9
Kuzidisha au kugawanya: ⓐ\(−117÷(−3)\) ⓑ\(3⋅13\) ⓒ\(7(−4)\) ⓓ\(−42÷6\).
- Jibu
-
ⓐ 39 ⓑ 39 ⓒ -28 ⓓ -7
Tunapozidisha idadi kwa 1, matokeo ni namba sawa. Kila wakati tunapozidisha idadi kwa -1, tunapata kinyume chake!
\[−1a=−a\]
Kuzidisha idadi kwa\(−1\) anatoa kinyume chake.
Kurahisisha Maneno na Integers
Nini kinatokea wakati kuna idadi zaidi ya mbili katika kujieleza? Utaratibu wa shughuli bado unatumika wakati hasi zinajumuishwa. Kumbuka Tafadhali udhuru Shangazi wangu Mpendwa Sally?
Hebu jaribu mifano fulani. Tutaweza kurahisisha maneno ambayo hutumia shughuli zote nne na integers-Aidha, kutoa, kuzidisha, na mgawanyiko. Kumbuka kufuata utaratibu wa shughuli.
Kurahisisha: ⓐ\((−2)^4\) ⓑ\(−2^4\).
- Jibu
-
Angalia tofauti katika sehemu (a) na (b). Katika sehemu (a), exponent ina maana ya kuongeza yaliyo katika mabano, ya -2 kwa 4 th nguvu. Katika sehemu (b), exponent ina maana ya kuongeza tu 2 kwa 4 th nguvu na kisha kuchukua kinyume.
ⓐ
\(\begin{array}{lc} \text{} & (−2)^4 \\ \text{Write in expanded form.} & (−2)(−2)(−2)(−2) \\ \text{Multiply.} & 4(−2)(−2) \\ \text{Multiply.} & −8(−2) \\ \text{Multiply.} & 16 \end{array}\)ⓑ
\(\begin{array}{lc} \text{} & −2^4 \\ \text{Write in expanded form.} & −(2·2·2·2) \\ \text{We are asked to find} & \text{} \\ \text{the opposite of }24. & \text{} \\ \text{Multiply.} & −(4·2·2) \\ \text{Multiply.} & −(8·2) \\ \text{Multiply.} & −16 \end{array}\)
Kurahisisha: ⓐ\((−3)^4\) ⓑ\(−3^4\).
- Jibu
-
ⓐ 81 ⓑ -81
Kurahisisha: ⓐ\((−7)^2\) ⓑ\(−7^2\).
- Jibu
-
ⓐ 49 ⓑ -49
Mfano wa mwisho ulituonyesha tofauti kati ya\((−2)^4\) na\(−2^4\). Tofauti hii ni muhimu ili kuzuia makosa ya baadaye. Mfano unaofuata unatukumbusha kuzidisha na kugawanya ili kushoto kwenda kulia.
Kurahisisha: ⓐ\(8(−9)÷(−2)^3\) ⓑ\(−30÷2+(−3)(−7)\).
- Jibu
-
ⓐ
\(\begin{array}{lc} \text{} & 8(−9)÷(−2)^3 \\ \text{Exponents first.} & 8(−9)÷(−8) \\ \text{Multiply.} & −72÷(−8) \\ \text{Divide.} & 9 \end{array}\)
ⓑ
\(\begin{array}{lc} \text{} & −30÷2+(−3)(−7) \\ \text{Multiply and divide} \\ \text{left to right, so divide first.} & −15+(−3)(−7) \\ \text{Multiply.} & −15+21 \\ \text{Add.} & 6 \end{array}\)
Kurahisisha: ⓐ\(12(−9)÷(−3)^3\) ⓑ\(−27÷3+(−5)(−6).\)
- Jibu
-
ⓐ 4 ⓑ 21
Kurahisisha: ⓐ\(18(−4)÷(−2)^3\) ⓑ\(−32÷4+(−2)(−7).\)
- Jibu
-
ⓐ 9 ⓑ 6
Tathmini Maneno ya kutofautiana na Integers
Kumbuka kwamba kutathmini maneno ina maana ya kubadilisha idadi kwa variable katika kujieleza. Sasa tunaweza kutumia namba hasi pamoja na idadi nzuri.
Tathmini\(4x^2−2xy+3y^2\) lini\(x=2,y=−1\).
- Jibu
-
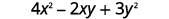
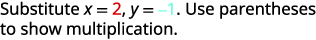
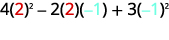
Kurahisisha watetezi. 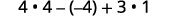
Kuzidisha. 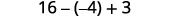
Ondoa. 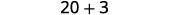
Ongeza. 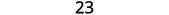
Tathmini:\(3x^2−2xy+6y^2\) wakati\(x=1,y=−2\).
- Jibu
-
31
Tathmini:\(4x^2−xy+5y^2\) wakati\(x=−2,y=3\).
- Jibu
-
67
Tafsiri Maneno kwa Maneno na Integers
Kazi yetu ya awali kutafsiri Kiingereza hadi algebra pia inatumika kwa misemo ambayo ni pamoja na idadi nzuri na hasi.
Tafsiri na kurahisisha: jumla ya 8 na -12, iliongezeka kwa 3.
- Jibu
-
\(\begin{array}{lc} \text{} & \text{the } \textbf{sum } \underline{\text{of}} \; –8 \; \underline{\text{and}} −12 \text{ increased by } 3 \\ \text{Translate.} & [8+(−12)]+3 \\ \text{Simplify. Be careful not to confuse the} \; \; \; \; \; \; \; \; \; \; & (−4)+3 \\ \text{brackets with an absolute value sign.} \\ \text{Add.} & −1 \end{array}\)
Tafsiri na kurahisisha jumla ya 9 na -16, iliongezeka kwa 4.
- Jibu
-
\((9+(−16))+4;−3\)
Tafsiri na kurahisisha jumla ya -8 na -12, iliongezeka kwa 7.
- Jibu
-
\((−8+(−12))+7;−13\)
Tumia Integers katika Maombi
Tutaelezea mpango wa kutatua programu. Ni vigumu kupata kitu kama hatujui nini sisi ni kuangalia kwa au nini kuiita! Kwa hiyo tunapotatua programu, sisi kwanza tunahitaji kuamua ni shida gani inatuuliza tupate. Kisha tutaandika maneno ambayo inatoa taarifa ili kuipata. Tutaweza kutafsiri maneno katika kujieleza na kisha kurahisisha kujieleza ili kupata jibu. Hatimaye, sisi muhtasari jibu katika sentensi ili kuhakikisha ni mantiki.
Joto la Kendallville, Indiana asubuhi moja lilikuwa digrii 11. Kufikia katikati ya mchana, halijoto lilikuwa limeshuka hadi nyuzi -9,19. Ilikuwa tofauti gani katika joto la asubuhi na alasiri?
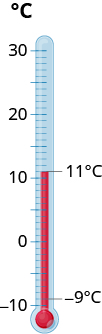
- Jibu
-






Joto la Anchorage, Alaska asubuhi moja lilikuwa digrii 15. Katikati ya mchana joto lilikuwa limeshuka hadi digrii 30 chini ya sifuri. Ilikuwa tofauti gani katika joto la asubuhi na alasiri?
- Jibu
-
Tofauti katika joto ilikuwa nyuzi 45 Fahrenheit.
Joto la Denver lilikuwa -6 digrii wakati wa chakula cha mchana. Kufikia machweo joto lilikuwa limeshuka hadi nyuzi -15. Ilikuwa tofauti gani katika joto la chakula cha mchana na jua?
- Jibu
-
Tofauti katika joto ilikuwa digrii 9.
- Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
- Tambua kile tunachoulizwa kupata.
- Andika maneno ambayo inatoa taarifa ili kuipata.
- Tafsiri maneno kwa kujieleza.
- Kurahisisha usemi.
- Jibu swali kwa sentensi kamili.
Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na integers.
- Kuondoa Integers na Counters
Dhana muhimu
- \[\begin{align} & −a \text{ means the opposite of the number }a \\ & \text{The notation} −a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
- Thamani kamili ya namba ni umbali wake kutoka 0 kwenye mstari wa namba.
Thamani kamili ya nambari n imeandikwa kama\(|n|\) na\(|n|≥0\) kwa namba zote.
Maadili kamili daima ni makubwa kuliko au sawa na sifuri.
- \[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
\(a−b=a+(−b)\)
Ondoa Mali Kutoa idadi ni sawa na kuongeza kinyume chake.- Kwa kuzidisha na mgawanyiko wa namba mbili zilizosainiwa:
Ikiwa ishara ni sawa, matokeo ni chanya.Ishara sawa Matokeo • Chanya mbili Chanya • Mbili hasi Chanya
Ikiwa ishara ni tofauti, matokeo ni hasi.Ishara tofauti Matokeo • Chanya na hasi Hasi • Hasi na chanya Hasi - Kuzidisha kwa\(−1\)
\(−1a=−a\)
Kuzidisha idadi kwa\(−1\) anatoa kinyume chake.
- Jinsi ya kutumia Integers katika Maombi.
- Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka
- Tambua kile tunachoulizwa kupata.
- Andika maneno ambayo inatoa taarifa ili kuipata.
- Tafsiri maneno kwa kujieleza.
- Kurahisisha usemi.
- Jibu swali kwa sentensi kamili.
faharasa
- thamani kamili
- Thamani kamili ya namba ni umbali wake kutoka\(0\) kwenye mstari wa namba.
- namba kamili
- Nambari nzima na kupinga kwao huitwa integers.
- idadi hasi
- Hesabu chini\(0\) ya idadi hasi.
- kinyume
- Kinyume cha namba ni namba ambayo ni umbali sawa kutoka sifuri kwenye mstari wa namba lakini upande wa pili wa sifuri.


