1.2E: Mazoezi

Last updated
Save as PDF

Page ID: 176168

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Mazoezi hufanya kamili

Tambua Multiples na Mambo

Katika mazoezi yafuatayo, tumia vipimo vya mgawanyiko ili kuamua kama kila namba inagawanyika na 2, na 3, na 5, na 6, na 10.

1. $84$

Jibu: Inagawanyika na 2, 3, 6

2. $96$

3. $896$

Jibu: Imegawanyika na 2

4. $942$

5. $22,335$

Jibu: Kugawanyika na 3, 5

6. $39,075$

Kupata factorizations Mkuu na Multiples angalau kawaida

Katika mazoezi yafuatayo, pata factorization kuu.

7. $86$

Jibu: $2⋅43$

8. $78$

9. $455$

Jibu: $5⋅7⋅13$

10. $400$

11. $432$

Jibu: $2⋅2⋅2⋅2⋅3⋅3⋅3$

12. $627$

Katika mazoezi yafuatayo, pata angalau ya kawaida ya kila jozi ya namba kwa kutumia njia kuu ya sababu.

13. $8,\; 12$

Jibu: $24$

14. $12,\; 16$

15. $28,\; 40$

Jibu: $280$

16. $84, \;90$

17. $55, \;88$

Jibu: $440$

18. $60, \;72$

Kurahisisha Maneno Kutumia Utaratibu wa Uendeshaji

Katika mazoezi yafuatayo, kurahisisha kila kujieleza.

19. $2^3−12÷(9−5)$

Jibu: $5$

20. $3^2−18÷(11−5)$

21. $2+8(6+1)$

Jibu: $58$

22. $4+6(3+6)$

23. $20÷4+6(5−1)$

Jibu: $29$

24. $33÷3+4(7−2)$

25. $3(1+9⋅6)−4^2$

Jibu: $149$

26. $5(2+8⋅4)−7^2$

27. $2[1+3(10−2)]$

Jibu: $50$

28. $5[2+4(3−2)]$

29. $8+2[7−2(5−3)]−3^2$

Jibu: $5$

30. $10+3[6−2(4−2)]−2^4$

Tathmini ya Kuelezea

Katika mazoezi yafuatayo, tathmini maneno yafuatayo.

31. Wakati$x=2$,

a.$x^6$

b.$4^x$

c.$2x^2+3x−7$

Jibu: a. 64
b. 16
c. 7

32. Wakati$x=3$,

a.$x^5$

b.$5x$

c.$3x^2−4x−8$

33. Wakati$x=4$ na$y=1$

$x^2+3xy−7y^2$

Jibu: $21$

34. Wakati$x=3$ na$y=2$

$6x^2+3xy−9y^2$

35. Wakati$x=10$ na$y=7$

$(x−y)^2$

Jibu: $9$

36. Wakati$a=3$ na$b=8$

$a^2+b^2$

Kurahisisha Maneno kwa Kuchanganya Kama Masharti

Katika mazoezi yafuatayo, kurahisisha maneno yafuatayo kwa kuchanganya maneno kama hayo.

37. $7x+2+3x+4$

Jibu: $10x+6$

38. $8y+5+2y−4$

39. $10a+7+5a−2+7a−4$

Jibu: $22a+1$

40. $7c+4+6c−3+9c−1$

41. $3x^2+12x+11+14x^2+8x+5$

Jibu: $17x^2+20x+16$

42. $5b^2+9b+10+2b^2+3b−4$

Tafsiri Maneno ya Kiingereza kwa kujieleza Algebraic

Katika mazoezi yafuatayo, tafsiri maneno katika maneno ya algebraic.

43. a. tofauti ya$5x^2$ na$6xy$

b. quotient ya$6y^2$ na$5x$

c. ishirini na moja zaidi$y^2$

d.$6x$ chini ya$81x^2$

Jibu

a.$5x^2−6xy$ b.$\frac{6y^2}{5x}$

c.$y^2+21$ d.$81x^2−6x$

44. a. tofauti ya$17x^2$ na$17x^2$ na$5xy$

b. quotient ya$8y^3$ na$3x$

c. kumi na nane zaidi ya$a^2$;

d.$11b$ chini ya$100b^2$

45. a. jumla ya$4ab^2$ na$3a^2b$

b. bidhaa ya$4y^2$ na$5x$

c. kumi na tano zaidi ya$m$

d.$9x$ chini ya$121x^2$

Jibu

a.$4ab^2+3a^2b$ b.$20xy^2$

c.$m+15$ d.$121x^2−9x$$9x<121x^2$

46. a. jumla ya$3x^2y$ na$7xy^2$

b. bidhaa ya$6xy^2$ na$4z$

c Kumi na mbili zaidi$3x^2$

d.$7x^2$ chini ya$63x^3$

47. a. mara nane tofauti ya$y$ na tisa

b. tofauti ya mara nane$y$ na$9$

Jibu: a.$8(y−9)$
b.$8y−9$

48. a. mara saba tofauti ya$y$ na moja

b. tofauti ya mara saba$y$ na$1$

49. a. mara tano jumla ya$3x$ na$y$

b. jumla ya mara tano$3x$ na$y$

Jibu: a.$5(3x+y)$
b.$15x+y$

50. a. mara kumi na moja jumla ya$4x2$ na$5x$

b. jumla ya mara kumi na moja$4x^2$ na$5x$

51. Eric ina mwamba na nchi nyimbo kwenye orodha ya kucheza yake. Idadi ya nyimbo za mwamba ni 14 zaidi ya mara mbili idadi ya nyimbo za nchi. Hebu c kuwakilisha idadi ya nyimbo za nchi. Andika maneno kwa idadi ya nyimbo za mwamba.

Jibu: $14>2c$

52. Idadi ya wanawake katika darasa la Takwimu ni 8 zaidi ya mara mbili idadi ya wanaume. Hebu$m$ kuwakilisha idadi ya wanaume. Andika maneno kwa idadi ya wanawake.

53. Greg ina nickels na pennies katika mfuko wake. Idadi ya pennies ni saba chini ya tatu idadi ya nickels. Hebu n kuwakilisha idadi ya nickels. Andika maneno kwa idadi ya pennies.

Jibu: $3n-7$

54. Jeannette ina$$5$ na$$10$ bili katika mkoba wake. Idadi ya fives ni tatu zaidi ya mara sita idadi ya makumi. Hebu$t$ kuwakilisha idadi ya makumi. Andika maneno kwa idadi ya fives.

Mazoezi ya kuandika

55. Eleza kwa maneno yako mwenyewe jinsi ya kupata factorization kuu ya nambari ya composite.

Jibu: Majibu yatatofautiana.

56. Kwa nini ni muhimu kutumia utaratibu wa shughuli ili kurahisisha kujieleza?

57. Eleza jinsi unavyotambua maneno kama hayo katika maneno$8a^2+4a+9−a^2−1.$

Jibu: Majibu yatatofautiana.

58. Eleza tofauti kati ya maneno “mara 4 jumla ya x na y” na “jumla ya mara 4 x na y”.

Self Check

Tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

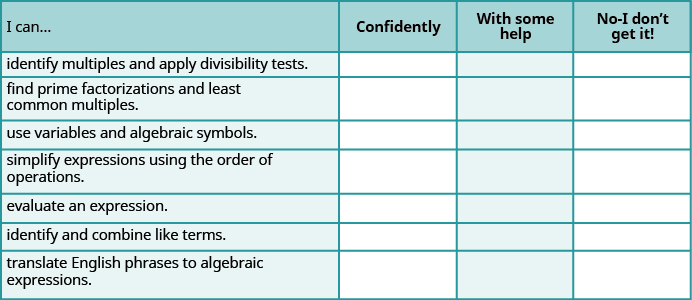
$Jedwali hili lina nguzo 4, safu 7 na mstari wa kichwa. Mstari wa kichwa huandika kila safu ninayoweza, kwa ujasiri, kwa msaada na hapana, siipati. Safu ya kwanza ina kauli zifuatazo: kutambua wingi na kutumia vipimo vya mgawanyiko, kupata factorizations mkuu na mafungu angalau ya kawaida, kutumia vigezo na alama za algebraic, kurahisisha maneno kwa kutumia utaratibu wa shughuli, kutathmini kujieleza, kutambua na kuchanganya kama maneno, kutafsiri Kiingereza misemo kwa maneno ya algebraic. Nguzo zilizobaki ni tupu.$

b Kama wengi wa hundi yako walikuwa:

... kwa ujasiri. Hongera! Umefanikiwa malengo katika sehemu hii. Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum.

... kwa msaada fulani. Hii lazima kushughulikiwa haraka kwa sababu mada huna bwana kuwa mashimo katika barabara yako ya mafanikio. Katika hesabu kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha kuwa na msingi imara kabla ya kuendelea. Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?

... hapana - Siipati! Hii ni ishara ya onyo na haipaswi kupuuza. Unapaswa kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.