1.2: Tumia Lugha ya Algebra
- Page ID
- 176150
Mwishoni mwa sehemu hii, utaweza:
- Kupata sababu, factorizations mkuu, na mafungu angalau ya kawaida
- Tumia vigezo na alama za algebraic
- Kurahisisha maneno kwa kutumia utaratibu wa shughuli
- Tathmini ya kujieleza
- Tambua na kuchanganya maneno kama
- Tafsiri maneno ya Kiingereza kwa kujieleza kwa algebraic
Sura hii inalenga kuwa mapitio mafupi ya dhana ambazo zitahitajika katika kozi ya Kati ya Algebra. Utangulizi wa kina zaidi wa mada yaliyofunikwa katika sura hii inaweza kupatikana katika sura ya Elementary Algebra, Misingi.
Kupata Mambo, Mkuu factorizations, na Multiples angalau kawaida
Nambari 2, 4, 6, 8, 10, 12 huitwa wingi wa 2. nyingi ya 2 inaweza kuandikwa kama bidhaa ya idadi kuhesabu na 2.
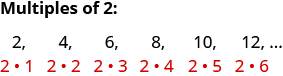
Vile vile, nyingi ya 3 itakuwa bidhaa ya idadi ya kuhesabu na 3.

Tunaweza kupata wingi wa idadi yoyote kwa kuendelea na mchakato huu.
| Idadi ya Kuhesabu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wingi wa 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| Wingi wa 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| Wingi wa 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| Wingi wa 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Wingi wa 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| Wingi wa 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| Wingi wa 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| Wingi wa 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
idadi ni nyingi ya\(n\) kama ni bidhaa ya idadi kuhesabu na\(n\).
Njia nyingine ya kusema kwamba 15 ni nyingi ya 3 ni kusema kwamba 15 ni mgawanyiko na 3. Hiyo ina maana kwamba wakati sisi kugawanya 3 katika 15, sisi kupata idadi kuhesabu. Kwa kweli,\(15÷3\) ni\(5\), hivyo\(15\) ni\(5⋅3\).
Kama idadi\(m\) ni nyingi ya\(n\), basi\(m\) ni mgawanyiko na\(n\).
Kama tungekuwa na kuangalia kwa chati katika wingi wa idadi 2 kwa 9, tungeweza kugundua zifuatazo vipimo mgawanyiko:
Nambari inagawanyika na:
- 2 ikiwa tarakimu ya mwisho ni 0, 2, 4, 6, au 8.
- 3 ikiwa jumla ya tarakimu inagawanyika na 3.
- 5 ikiwa tarakimu ya mwisho ni 5 au 0.
- 6 ikiwa inagawanyika na 2 na 3.
- 10 ikiwa inaisha na 0.
Je 5,625 kugawanyika na
- 2?
- 3?
- 5 au 10?
- 6?
- Jibu
-
a.
\(\text{Is 5,625 divisible by 2?}\)
\( \begin{array}{ll} \text{Does it end in 0, 2, 4, 6 or 8?} & {\text{No.} \\ \text{5,625 is not divisible by 2.}} \end{array}\) - b.
\(\text{5,625 divisible by 3?}\)
\(\begin{array}{ll} {\text{What is the sum of the digits?} \\ \text{Is the sum divisible by 3?}} & {5+6+2+5=18 \\ \text{Yes.} \\ \text{5,625 is divisible by 3.}}\end{array}\) - c.
\(\text{Is 5,625 divisible by 5 or 10?}\)
\(\begin{array}{ll} \text{What is the last digit? It is 5.} & \text{5,625 is divisible by 5 but not by 10.} \end{array}\)d.\(\text{Is 5,625 divisible by 6?}\)
\(\begin{array}{ll}\text{Is it divisible by both 2 and 3?} & {\text{No, 5,625 is not divisible by 2, so 5,625 is} \\ \text{not divisible by 6.}} \end{array}\)
ni 4,962 mgawanyiko na. 2? b. 3? c. 5? d. 6? e. 10?
- Jibu
-
a. ndiyo b. ndiyo c. hapana d. ndiyo e. hapana
ni 3,765 mgawanyiko na. 2? b. 3? c. 5? d. 6? e. 10?
- Jibu
-
a. hakuna b. ndiyo c. ndiyo d. hapana e. hapana
Katika hisabati, mara nyingi kuna njia kadhaa za kuzungumza juu ya mawazo sawa. Hadi sasa, tumeona kwamba kama\(m\) ni nyingi ya\(n\), tunaweza kusema kwamba\(m\) ni mgawanyiko na\(n\). Kwa mfano, tangu 72 ni nyingi ya 8, tunasema 72 inagawanyika na 8. Tangu 72 ni nyingi ya 9, tunasema 72 ni mgawanyiko na 9. Tunaweza kueleza hii bado njia nyingine.
Tangu\(8·9=72\), tunasema kwamba 8 na 9 ni sababu za 72. Tunapoandika\(72=8·9\), tunasema tuna factored 72.
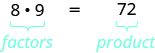
Njia nyingine za kuzingatia\(72\) ni\(1·72, \; 2·36, \; 3·24, \; 4·18,\) na\(6⋅12\). idadi 72 ina mambo mengi:\(1,\,2,\,3,\,4,\,6,\,8,\,9,\,12,\,18,\,24,\,36,\) na\(72\).
Kama\(a\) na\(b\) ni kuhesabu idadi, na\(a·b=m\), basi\(a\) na\(b\) ni sababu ya\(m\).
Nambari zingine, kama vile 72, zina mambo mengi. Nambari nyingine zina sababu mbili tu. Nambari kuu ni namba ya kuhesabu zaidi ya 1 ambayo sababu zake pekee ni 1 na yenyewe.
Nambari kuu ni namba ya kuhesabu zaidi ya 1 ambayo sababu zake pekee ni 1 na namba yenyewe.
Nambari ya composite ni namba ya kuhesabu ambayo si mkuu. Nambari ya composite ina mambo mengine zaidi ya 1 na namba yenyewe.
Nambari za kuhesabu kutoka 2 hadi 20 zimeorodheshwa kwenye meza na mambo yao. Hakikisha kukubaliana na lebo ya “mkuu” au “Composite” kwa kila mmoja!
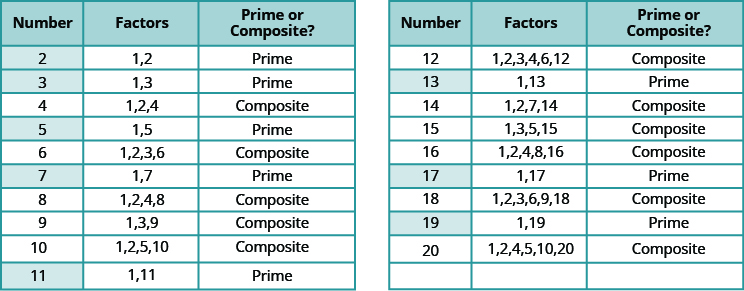
Nambari kuu chini ya 20 ni 2, 3, 5, 7, 11, 13, 17, na 19. Kumbuka kwamba tu hata mkuu idadi ni 2.
Nambari ya composite inaweza kuandikwa kama bidhaa ya kipekee ya primes. Hii inaitwa factorization mkuu wa idadi. Kupata factorization mkuu wa idadi Composite itakuwa muhimu katika mada nyingi katika kozi hii.
Factorization mkuu wa idadi ni bidhaa ya idadi ya mkuu ambayo ni sawa na idadi.
Ili kupata factorization kuu ya nambari ya composite, pata mambo mawili ya nambari na uitumie kuunda matawi mawili. Kama sababu ni mkuu, tawi hilo ni kamili. Circle kwamba mkuu. Vinginevyo ni rahisi kupoteza wimbo wa idadi mkuu.
Ikiwa sababu sio mkuu, pata sababu mbili za nambari na uendelee mchakato. Mara baada ya matawi yote yamezunguka primes mwishoni, factorization imekamilika. Nambari ya composite sasa inaweza kuandikwa kama bidhaa ya namba kuu.
Sababu 48.
- Jibu
-


.jpg)
Tunasema\(2⋅2⋅2⋅2⋅3\) ni factorization mkuu wa 48. Kwa ujumla tunaandika primes katika utaratibu wa kupanda. Hakikisha kuzidisha mambo ili kuthibitisha jibu lako. \(2⋅2⋅2⋅2⋅3\)ni factorization mkuu wa 48. Kwa ujumla tunaandika primes katika utaratibu wa kupanda. Hakikisha kuzidisha mambo ili kuthibitisha jibu lako.
Kama sisi kwanza factored 48 kwa njia tofauti, kwa mfano kama\(6·8\), matokeo bado kuwa sawa. Kumaliza factorization mkuu na uhakikishe hili mwenyewe.
Kupata factorization mkuu wa\(80\).
- Jibu
-
\(2⋅2⋅2⋅2⋅5\)
Kupata factorization mkuu wa\(60\).
- Jibu
-
\(2⋅2⋅3⋅5\)
- Pata mambo mawili ambayo bidhaa ni nambari iliyotolewa, na utumie namba hizi kuunda matawi mawili.
- Kama sababu ni mkuu, tawi hilo ni kamili. Mzunguko mkuu, kama jani kwenye mti.
- Ikiwa jambo sio mkuu, andika kama bidhaa ya mambo mawili na uendelee mchakato.
- Andika nambari ya composite kama bidhaa ya primes zote zilizozunguka.
Moja ya sababu tunayoangalia primes ni kutumia mbinu hizi ili kupata idadi ndogo ya kawaida ya namba mbili. Hii itakuwa na manufaa wakati sisi kuongeza na kuondoa sehemu ndogo na denominators tofauti.
Nyingi ya kawaida (LCM) ya namba mbili ni idadi ndogo zaidi ambayo ni nyingi ya namba zote mbili.
Ili kupata idadi ndogo ya kawaida ya namba mbili tutatumia Njia ya Mambo Mkuu. Hebu tupate LCM ya 12 na 18 kwa kutumia sababu zao kuu.
Kupata angalau kawaida nyingi (LCM) ya 12 na 18 kutumia mkuu sababu mbinu.
- Jibu
-

.jpg)


Angalia kwamba sababu kuu za 12\((2·2·3)\) na sababu kuu za 18\((2⋅3⋅3)\) zinajumuishwa katika LCM\((2·2·3·3)\). Hivyo 36 ni angalau kawaida nyingi ya 12 na 18.
Kwa kulinganisha juu ya primes ya kawaida, kila sababu ya kawaida ya kawaida hutumiwa mara moja tu. Kwa njia hii una uhakika kwamba 36 ni angalau kawaida nyingi.
Pata LCM ya 9 na 12 kwa kutumia Njia ya Mambo Mkuu.
- Jibu
-
36
Kupata LCM ya 18 na 24 kwa kutumia Mkuu Mambo Method.
- Jibu
-
72
- Andika kila nambari kama bidhaa ya primes.
- Orodha ya primes ya kila idadi. Mechi primes wima ikiwezekana.
- Kuleta chini nguzo.
- Kuzidisha mambo.
Tumia Vigezo na Algebraic Algebraic
Katika algebra, tunatumia barua ya alfabeti kuwakilisha namba ambayo thamani yake inaweza kubadilika. Tunaita hii variable na barua kawaida kutumika kwa ajili ya vigezo ni\(x,\,y,\,a,\,b,\) na\(c.\)
Variable ni barua inayowakilisha namba ambayo thamani yake inaweza kubadilika.
Nambari ambayo thamani yake daima inabakia sawa inaitwa mara kwa mara.
Mara kwa mara ni namba ambayo thamani yake daima inakaa sawa.
Kuandika algebraically, tunahitaji baadhi ya alama operesheni kama vile idadi na vigezo. Kuna aina kadhaa za alama tutakayotumia. Kuna shughuli nne za msingi za hesabu: kuongeza, kuondoa, kuzidisha, na mgawanyiko. Tutaorodhesha alama zilizotumiwa kuonyesha shughuli hizi hapa chini.
| Operesheni | Nukuu | Sema: | Matokeo yake ni... |
|---|---|---|---|
| Ongezeko | \(a+b\) | \(a\)pamoja\(b\) | jumla ya\(a\) na\(b\) |
| Kutoa | \(a−b\) | \(a\)minus\(b\) | tofauti ya\(a\) na\(b\) |
| Kuzidisha | \(a⋅b,\,ab,\,(a)(b),\,(a)b,\,a(b)\) | \(a\)mara\(b\) | bidhaa ya\(a\) na\(b\) |
| Mgawanyiko | \(a÷b,\,\space a/b,\,\space\frac{a}{b},\,\space b \overline{\smash{)}a}\) | \(a\)kugawanywa na\(b\) | quotient ya\(a\) na\(b\); \(a\) inaitwa gawio, na\(b\) inaitwa mgawanyiko |
Wakati kiasi mbili zina thamani sawa, tunasema ni sawa na kuunganisha kwa ishara sawa.
\(a=b\)ni kusoma "\(a\)ni sawa na\(b\).”
Ishara “\(=\)” inaitwa ishara sawa.
Kwenye mstari wa nambari, nambari zinaongezeka zaidi wanapoenda kutoka kushoto kwenda kulia. Mstari wa nambari unaweza kutumika kuelezea alama “\(<\)” na “\(>\)”.

Maneno\(a<b\) au\(a>b\) yanaweza kusomwa kutoka kushoto kwenda kulia au kulia kwenda kushoto, ingawa kwa Kiingereza tunasoma kutoka kushoto kwenda kulia. Kwa ujumla,
\[a<b \text{ is equivalent to }b>a. \text{For example, } 7<11 \text{ is equivalent to }11>7.\]
\[a>b \text{ is equivalent to }b<a. \text{For example, } 17>4 \text{ is equivalent to }4<17.\]
| Alama za kukosekana | Maneno |
|---|---|
| \(a\neq b\) | \(a\)si sawa na\(b\). |
| \(a<b\) | \(a\)ni chini ya\(b\). |
| \(a\leq b\) | \(a\)ni chini ya au sawa na\(b\). |
| \(a>b\) | \(a\)ni kubwa kuliko\(b\). |
| \(a\geq b\) | \(a\)ni kubwa kuliko au sawa na\(b\). |
Alama za makundi katika algebra ni sawa na koma, koloni, na alama nyingine za punctuation kwa Kiingereza. Wao kusaidia kutambua kujieleza, ambayo inaweza kuwa na idadi, variable, au mchanganyiko wa idadi na vigezo kwa kutumia alama operesheni. Tutaanzisha aina tatu za alama za makundi sasa.
\[\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\]
Hapa ni baadhi ya mifano ya maneno ambayo yanajumuisha alama za makundi. Sisi kurahisisha maneno kama haya baadaye katika sehemu hii.
\[8(14−8) \qquad 21−3[2+4(9−8)] \qquad 24÷ \{13−2[1(6−5)+4]\}\]
Ni tofauti gani katika Kiingereza kati ya maneno na sentensi? Maneno yanaonyesha mawazo moja ambayo hayajakamilika yenyewe, lakini sentensi hutoa taarifa kamili. Sentensi ina somo na kitenzi. Katika algebra, tuna maneno na equations.
Maneno ni namba, kutofautiana, au mchanganyiko wa namba na vigezo kwa kutumia alama za uendeshaji.
\[\begin{array}{lll} \textbf{Expression} & \textbf{Words} & \textbf{English Phrase} \\ \mathrm{3+5} & \text{3 plus 5} & \text{the sum of three and five} \\ \mathrm{n−1} & n\text{ minus one} & \text{the difference of } n \text{ and one} \\ \mathrm{6·7} & \text{6 times 7} & \text{the product of six and seven} \\ \frac{x}{y} & x \text{ divided by }y & \text{the quotient of }x \text{ and }y \end{array} \]
Angalia kwamba misemo ya Kiingereza hayafanyi sentensi kamili kwa sababu maneno hayana kitenzi.
Equation ni maneno mawili yanayounganishwa na ishara sawa. Unaposoma maneno alama zinawakilisha katika equation, una sentensi kamili kwa Kiingereza. Ishara sawa inatoa kitenzi.
Equation ni maneno mawili yanayounganishwa na ishara sawa.
\[\begin{array}{ll} \textbf{Equation} & \textbf{English Sentence} \\ 3+5=8 & \text{The sum of three and five is equal to eight.} \\ n−1=14 & n \text{ minus one equals fourteen.} \\ 6·7=42 & \text{The product of six and seven is equal to forty-two.} \\ x=53 & x \text{ is equal to fifty-three.} \\ y+9=2y−3 & y \text{ plus nine is equal to two } y \text{ minus three.} \end{array}\]
Tuseme tunahitaji kuzidisha mara 2 tisa. Tunaweza kuandika hii kama\(2·2·2·2·2·2·2·2·2\). Hii ni tedious na inaweza kuwa vigumu kuweka wimbo wa 2s wale wote, hivyo sisi kutumia exponents. Tunaandika\(2·2·2\) kama\(\mathrm{2^3}\) na\(2·2·2·2·2·2·2·2·2\) kama\(2^9\). Katika maneno kama vile\(2^3\), 2 inaitwa msingi na 3 inaitwa exponent. Mtazamaji anatuambia mara ngapi tunahitaji kuzidisha msingi.

Tunasema\(2^3\) ni katika nukuu kielelezo na\(2·2·2\) iko katika nukuu iliyopanuliwa.
\(a^n\)ina maana kuzidisha\(n\) mambo ya idadi\(a\).
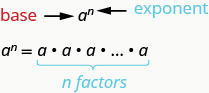
Maneno\(a^n\)\(a\) yanasomewa kwa\(n^{th}\) nguvu.
Wakati sisi kusoma\(a^n\)\(“a\) kuhusu\(n^{th}\) nguvu”, sisi kawaida kusoma:
\[\begin{array}{cc} a^2 & “a \text{ squared}” \\ a^3 & “a \text{ cubed}” \end{array}\]
Tutaona baadaye kwa nini\(a^2\) na\(a^3\) kuwa na majina maalum.
Jedwali linaonyesha jinsi sisi kusoma baadhi ya maneno na exponents.
| Ufafanuzi | Katika Maneno | |
|---|---|---|
| 7 2 | 7 kwa nguvu ya pili au | 7 mraba |
| 5 3 | 5 kwa nguvu ya tatu au | 5 mchemraba |
| 9 4 | 9 kwa nguvu ya nne | |
| 12 5 | 12 kwa nguvu ya tano |
Kurahisisha Maneno Kutumia Utaratibu wa Uendeshaji
Kurahisisha kujieleza ina maana ya kufanya hesabu yote iwezekanavyo. Kwa mfano, ili kurahisisha\(\mathrm{4·2+1}\)\(\mathrm{4⋅2}\) tunataka kwanza kuzidisha kupata 8 na kisha kuongeza 1 kupata 9. Tabia nzuri ya kuendeleza ni kufanya kazi chini ya ukurasa, kuandika kila hatua ya mchakato chini ya hatua ya awali. Mfano ulioelezwa tu utaonekana kama hii:
\[ 4⋅2+1 \\ 8+1 \\ 9\]
Kwa kutotumia ishara sawa unaporahisisha usemi, unaweza kuepuka maneno ya kuchanganyikiwa na milinganyo.
Ili kurahisisha kujieleza, fanya shughuli zote katika maneno.
Tumeanzisha alama nyingi na nukuu zilizotumiwa katika algebra, lakini sasa tunahitaji kufafanua utaratibu wa shughuli. Vinginevyo, maneno yanaweza kuwa na maana tofauti, na inaweza kusababisha maadili tofauti.
Kwa mfano, fikiria maneno\(4+3⋅7\). Baadhi ya wanafunzi kurahisisha hii kupata 49, kwa kuongeza\(4+3\) na kisha kuzidisha matokeo hayo kwa 7. Wengine hupata 25, kwa kuzidisha\(3·7\) kwanza na kisha kuongeza 4.
Maneno sawa yanapaswa kutoa matokeo sawa. Hivyo wanahisabati walianzisha baadhi ya miongozo inayoitwa utaratibu wa shughuli.
- Mabano na Alama Zingine za Kundi
- Kurahisisha maneno yote ndani ya mabano au alama nyingine za makundi, kufanya kazi kwenye mabano ya ndani ya kwanza.
- Watetezi
- Kurahisisha maneno yote na exponents.
- Kuzidisha na Idara
- Fanya kuzidisha na mgawanyiko wote ili kutoka kushoto kwenda kulia. Shughuli hizi zina kipaumbele sawa.
- Kuongeza na Ondoa
- Fanya uongeze wote na uondoe kwa utaratibu kutoka kushoto kwenda kulia. Shughuli hizi zina kipaumbele sawa.
Wanafunzi mara nyingi huuliza, “Nitakumbuka jinsi gani?” Hapa ni njia ya kukusaidia kukumbuka: Chukua barua ya kwanza ya kila neno muhimu na ubadilishe maneno ya silly “Tafadhali udhuru Shangazi My Dear Sally”.
\[\begin{array}{ll} \text{Parentheses} & \text{Please} \\ \text{Exponents} & \text{Excuse} \\ \text{Multiplication Division} & \text{My Dear} \\ \text{Addition Subtraction} & \text{Aunt Sally} \end{array}\]
Ni vizuri kwamba “My y D sikio” huenda pamoja, kwa kuwa hii inatukumbusha kwamba kuzidisha kwangu na mgawanyiko wa d una kipaumbele sawa. Hatuna daima kuzidisha kabla ya mgawanyiko au daima kufanya mgawanyiko kabla ya kuzidisha. Tunawafanya ili kutoka kushoto kwenda kulia.
Vile vile, “Mshirika wa kitengo cha S” huenda pamoja na hivyo hutukumbusha kwamba kuongeza na uondoaji wake pia una kipaumbele sawa na tunawafanya kwa utaratibu kutoka kushoto kwenda kulia.
Kurahisisha:\(18÷6+4(5−2)\).
- Jibu
-
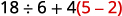
Mabano? Ndiyo, toa kwanza. 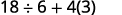
Watetezi? Hapana. Kuzidisha au mgawanyiko? Ndiyo. Gawanya kwanza kwa sababu tunazidisha na kugawanya kushoto kwenda kulia. 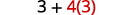
Yoyote kuzidisha nyingine au mgawanyiko? Ndiyo. Kuzidisha. 
Yoyote kuzidisha nyingine ya mgawanyiko? Hapana. Aidha yoyote au kuondoa? Ndiyo. Ongeza. 
Kurahisisha:\(30÷5+10(3−2).\)
- Jibu
-
16
Kurahisisha:\(70÷10+4(6−2).\)
- Jibu
-
23
Wakati kuna alama nyingi kambi, sisi kurahisisha mabano ndani ya kwanza na kufanya kazi nje.
Kurahisisha:\(5+2^3+3[6−3(4−2)].\)
- Jibu
-
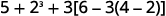
Je, kuna mabano yoyote (au alama nyingine za makundi)? Ndiyo. 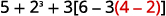
Kuzingatia mabano yaliyo ndani ya mabano. Ondoa. 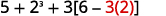
Endelea ndani ya mabano na uongeze. 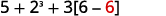
Endelea ndani ya mabano na uondoe. 
Maneno ndani ya mabano hayahitaji kurahisisha zaidi. Je, kuna exponents yoyote? Ndiyo. Kurahisisha watetezi. 
Je, kuna kuzidisha au mgawanyiko wowote? Ndiyo. Kuzidisha. 
Je, kuna kuongeza yoyote ya kuondoa? Ndiyo. Ongeza. 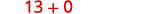
Ongeza. 
Kurahisisha:\(9+5^3−[4(9+3)].\)
- Jibu
-
86
Kurahisisha:\(7^2−2[4(5+1)].\)
- Jibu
-
1
Tathmini ya Kuelezea
Katika mifano michache iliyopita, sisi rahisi maneno kwa kutumia utaratibu wa shughuli. Sasa tutaweza kutathmini baadhi ya kujieleza - tena kufuatia utaratibu wa shughuli. Kutathmini njia ya kujieleza ina maana ya kupata thamani ya kujieleza wakati kutofautiana inabadilishwa na nambari iliyotolewa.
Kutathmini njia ya kujieleza ina maana ya kupata thamani ya kujieleza wakati kutofautiana inabadilishwa na nambari iliyotolewa.
Kutathmini usemi, badala ya idadi hiyo kwa variable katika kujieleza na kisha kurahisisha kujieleza.
Tathmini wakati\(x=4\): a.\(x^2\) b.\(3^x\) c\(2x^2+3x+8\).
- Jibu
-
a.
b.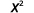
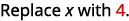

Matumizi ufafanuzi wa exponent. 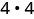
Kurahisisha. 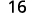
c.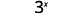
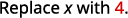

Matumizi ufafanuzi wa exponent. 
Kurahisisha. 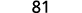
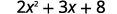
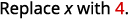
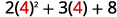
Fuata utaratibu wa shughuli. .jpg)
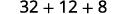
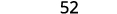
Tathmini wakati\(x=3\), a.\(x^2\) b.\(4^x\) c\(3x^2+4x+1\).
- Jibu
-
a. 9
b. 64
c 40
Tathmini wakati\(x=6\), a.\(x^3\) b.\(2^x\) c\(6x^2−4x−7\).
- Jibu
-
a. 216
b. 64
c 185
Tambua na Unganisha Kama Masharti
Maneno ya algebraic yanajumuishwa na maneno. Neno ni mara kwa mara, au bidhaa ya vigezo vya mara kwa mara na moja au zaidi.
Neno ni mara kwa mara au bidhaa ya vigezo vya mara kwa mara na moja au zaidi.
Mifano ya maneno ni\(7,\,y,\,5x^2,\,9a,\) na\(b^5\).
Mara kwa mara ambayo huzidisha variable inaitwa mgawo.
Mgawo wa neno ni mara kwa mara ambayo huzidisha kutofautiana kwa muda.
Fikiria mgawo kama namba mbele ya kutofautiana. Mgawo wa neno\(3x\) ni 3. Tunapoandika\(x\), mgawo ni 1, tangu\(x=1⋅x\).
Baadhi ya maneno hushiriki sifa za kawaida. Wakati maneno mawili ni constants au kuwa variable sawa na exponent, tunasema wao ni kama maneno.
Angalia masharti 6 yafuatayo. Ambayo inaonekana kuwa na sifa sawa?
\[5x \quad 7 \quad n^2 \quad 4 \quad 3x \quad 9n^2\]
Tunasema,
\(7\)na\(4\) ni kama maneno.
\(5x\)na\(3x\) ni kama maneno.
\(n^2\)na\(9n^2\) ni kama maneno.
Masharti ambayo ni ama constants au kuwa na vigezo sawa kukulia kwa nguvu sawa ni kuitwa kama maneno.
Ikiwa kuna maneno kama hayo katika kujieleza, unaweza kurahisisha maneno kwa kuchanganya maneno kama hayo. Sisi kuongeza coefficients na kuweka variable sawa.
\[\begin{array}{lc} \text{Simplify.} & 4x+7x+x \\ \text{Add the coefficients.} & 12x \end{array}\]
Kurahisisha:\(2x^2+3x+7+x^2+4x+5\).
- Jibu
-



Kurahisisha:\(3x^2+7x+9+7x^2+9x+8\).
- Jibu
-
\(10x^2+16x+17\)
Kurahisisha:\(4y^2+5y+2+8y^2+4y+5.\)
- Jibu
-
\(12y^2+9y+7\)
- Tambua maneno kama hayo.
- Panga upya maneno ili kama maneno ni pamoja.
- Kuongeza au Ondoa coefficients na kuweka variable sawa kwa kila kundi la maneno kama.
Tafsiri Maneno ya Kiingereza kwa kujieleza Algebraic
Sisi waliotajwa alama nyingi operesheni ambayo hutumiwa katika algebra. Sasa, tutatumia kutafsiri misemo ya Kiingereza katika maneno ya algebraic. alama na vigezo tumekuwa kuongelea kutusaidia kufanya hivyo. Jedwali linawafupisha.
| Operesheni | Maneno | Ufafanuzi |
|---|---|---|
| Ongezeko | \(a\)pamoja\(b\)
jumla ya\(a\) na\(b\) \(a\)iliongezeka kwa\(b\) \(b\)zaidi ya\(a\) jumla ya\(a\) na\(b\) \(b\)imeongezwa kwa\(a\) |
\(a+b\) |
| Kutoa | \(a\)minus\(b\)
tofauti ya\(a\) na\(b\) \(a\)ilipungua kwa\(b\) \(b\)chini ya\(a\) \(b\)imetolewa kutoka\(a\) |
\(a−b\) |
| Kuzidisha | \(a\)mara\(b\)
bidhaa ya\(a\) na\(b\) mara mbili\(a\) |
\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\) |
| Idara | \(a\)kugawanywa na\(b\)
quotient ya\(a\) na\(b\) uwiano wa\(a\) na\(b\) \(b\)imegawanywa katika\(a\) |
\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\) |
Angalia kwa karibu maneno haya kwa kutumia shughuli nne:

Kila maneno inatuambia kufanya kazi kwa namba mbili. Angalia maneno ya na kupata idadi.
Kila maneno inatuambia kufanya kazi kwa namba mbili. Angalia maneno ya na kupata idadi.
Tafsiri kila maneno ya Kiingereza katika usemi wa algebraic:
a. tofauti ya\(14x\) na\(9\)
b. quotient ya\(8y^2\) na\(3\)c. kumi na mbili zaidi\(y\)
d. saba chini ya\(49x^2\)
- Jibu
-
a. neno muhimu ni tofauti, ambayo inatuambia operesheni ni Ondoa. Angalia kwa maneno ya na t o kupata idadi ya Ondoa.
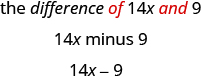
b. neno muhimu ni quotient, ambayo inatuambia operesheni ni mgawanyiko.

c. maneno muhimu ni zaidi ya. Wao kutuambia operesheni ni kuongeza. Zaidi ya maana “aliongeza kwa.”
\[\text{twelve more than }y \\ \text{twelve added to }y \\ y+12\]
d. maneno muhimu ni chini ya. Wanatuambia tuondoe. Chini ya maana “imetolewa kutoka.”
\[\text{seven less than }49x^2 \\ \text{seven subtracted from }49x^2 \\ 49x^2−7\]
Tafsiri maneno ya Kiingereza katika usemi wa algebraic:
a. tofauti ya\(14x^2\) na\(13\)
b. quotient ya\(12x\) na\(2\)
c.\(13\) zaidi\(z\)
d.\(18\) chini ya\(8x\)
- Jibu
-
a.\(14x^2−13\) b.\(12x÷2\)
c.\(z+13\) d.\(8x−18\)
Tafsiri maneno ya Kiingereza katika usemi wa algebraic:
a. jumla ya\(17y^2\) na\(19\)
b. bidhaa ya\(7\) na\(y\)
c. kumi na moja zaidi\(x\)
d. kumi na nne chini ya\(11a\)
- Jibu
-
a.\(17y^2+19\) b.\(7y\)
c.\(x+11\) d.\(11a−14\)
Tunaangalia kwa makini maneno ili kutusaidia kutofautisha kati ya kuzidisha jumla na kuongeza bidhaa.
Tafsiri maneno ya Kiingereza katika usemi wa algebraic:
a. mara nane jumla ya\(x\) na\(y\)
b. jumla ya mara nane\(x\) na\(y\)
- Jibu
-
Kuna operesheni mbili words— mara inatuambia kuzidisha na jumla inatuambia kuongeza.
a. kwa sababu sisi ni kuzidisha\(8\) mara jumla, tunahitaji mabano karibu jumla ya\(x\) na\(y\),\((x+y)\). Hii inatuwezesha kuamua jumla ya kwanza. (Kumbuka utaratibu wa shughuli.)
\[\text{eight times the sum of }x \text{ and }y \\ 8(x+y)\]
b Ili kuchukua jumla, tunatafuta maneno ya na kuona kile kinachoongezwa. Hapa tunachukua jumla ya mara nane\(x\) na\(y\).
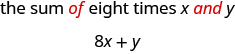
Tafsiri maneno ya Kiingereza katika usemi wa algebraic:
a. mara nne jumla ya\(p\) na\(q\)
b. jumla ya mara nne\(p\) na\(q\)
- Jibu
-
a.\(4(p+q)\) b.\(4p+q\)
Tafsiri maneno ya Kiingereza katika usemi wa algebraic:
a. tofauti ya mara mbili\(x\) na\(8\)
b. mara mbili tofauti ya\(x\) na\(8\)
- Jibu
-
a.\(2x−8\) b.\(2(x−8)\)
Baadaye katika kozi hii, tutaweza kutumia ujuzi wetu katika algebra kutatua maombi. Hatua ya kwanza itakuwa kutafsiri maneno ya Kiingereza kwa kujieleza kwa algebraic. Tutaona jinsi ya kufanya hivyo katika mifano miwili ijayo.
Urefu wa mstatili ni 14 chini ya upana. Hebu\(w\) kuwakilisha upana wa mstatili. Andika maneno kwa urefu wa mstatili.
- Jibu
-
\[\begin{array}{lc} \text{Write a phrase about the length of the rectangle.} & \text{14 less than the width} \\ \text{Substitute }w \text{ for “the width.”} & w \\ \text{Rewrite less than as subtracted from.} & \text{14 subtracted from } w \\ \text{Translate the phrase into algebra.} & w−14 \end{array}\]
Urefu wa mstatili ni 7 chini ya upana. Hebu\(w\) kuwakilisha upana wa mstatili. Andika maneno kwa urefu wa mstatili.
- Jibu
-
\(w−7\)
Upana wa mstatili ni\(6\) chini ya urefu. Hebu\(l\) kuwakilisha urefu wa mstatili. Andika maneno kwa upana wa mstatili.
- Jibu
-
\(l−6\)
maneno katika mfano ya zitatumika katika matatizo ya kawaida sarafu mchanganyiko tutaona hivi karibuni.
Juni ina dimes na robo katika mfuko wake. Idadi ya dimes ni saba chini ya mara nne idadi ya robo. Hebu\(q\) kuwakilisha idadi ya robo. Andika maneno kwa idadi ya dimes.
- Jibu
-
\[\begin{array}{lc} \text{Write a phrase about the number of dimes.} & \text{7 less than 4 times }q \\ \text{Translate 4 times }q. & \text{7 less than 4}q \\ \text{Translate the phrase into algebra.} & 4q−7 \end{array}\]
Geoffrey ana dimes na robo katika mfuko wake. Idadi ya dimes ni nane chini ya mara nne idadi ya robo. Hebu\(q\) kuwakilisha idadi ya robo. Andika maneno kwa idadi ya dimes.
- Jibu
-
\(4q−8\)
Lauren ana dimes na nickels katika mfuko wake. Idadi ya dimes ni tatu zaidi ya mara saba idadi ya nickels. Hebu\(n\) kuwakilisha idadi ya nickels. Andika maneno kwa idadi ya dimes.
- Jibu
-
\(7n+3\)
Dhana muhimu
- Uchunguzi
wa mgawanyiko Nambari inagawanyika na:
2 ikiwa tarakimu ya mwisho ni 0, 2, 4, 6, au 8.
3 ikiwa jumla ya tarakimu inagawanyika na 3.
5 ikiwa tarakimu ya mwisho ni 5 au 0.
6 ikiwa inagawanyika na 2 na 3.
10 ikiwa inaisha na 0. - Jinsi ya kupata factorization mkuu wa idadi Composite.
- Pata mambo mawili ambayo bidhaa ni nambari iliyotolewa, na utumie namba hizi kuunda matawi mawili.
- Kama sababu ni mkuu, tawi hilo ni kamili. Circle mkuu, kama bud juu ya mti.
- Ikiwa jambo sio mkuu, andika kama bidhaa ya mambo mawili na uendelee mchakato.
- Andika nambari ya composite kama bidhaa ya primes zote zilizozunguka.
- Jinsi ya Kupata angalau kawaida nyingi kwa kutumia mkuu sababu mbinu.
- Andika kila namba kama bidhaa ya primes.
- Orodha ya primes ya kila idadi. Mechi primes wima ikiwezekana.
- Kuleta chini nguzo.
- Kuzidisha mambo.
- Usawa Mkono
\(a=b\) ni kusoma “\(a\)ni sawa na\(b\).” Ishara “=” inaitwa ishara sawa. 
- Alama za kukosekana
Alama za kukosekana Maneno \(a≠b\) \(a\)si sawa na\(b\). \(a<b\) \(a\)ni chini ya\(b\). \(a≤b\) \(a\)ni chini ya au sawa na\(b\). \(a>b\) \(a\)ni kubwa kuliko\(b\). \(a≥b\) \(a\)ni kubwa kuliko au sawa na \(b\). - Kundi Alama\(\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\)
- Uthibitishaji wa kielelezo\(a^n\) unamaanisha \(a\)kuzidisha yenyewe, \(n\)mara. Maneno ya an yanasomewa \(a\)kwa\(n^{th}\) nguvu.
- Kurahisisha kujieleza
Ili kurahisisha kujieleza, fanya shughuli zote katika kujieleza. - Jinsi ya kutumia utaratibu wa shughuli.
- Mabano na Alama Zingine za Kundi
- Kurahisisha maneno yote ndani ya mabano au alama nyingine za makundi, kufanya kazi kwenye mabano ya ndani ya kwanza.
- Watetezi
- Kurahisisha maneno yote na exponents.
- Kuzidisha na Idara
- Fanya kuzidisha na mgawanyiko wote ili kutoka kushoto kwenda kulia. Shughuli hizi zina kipaumbele sawa.
- Kuongeza na Ondoa
- Fanya uongeze wote na uondoe kwa utaratibu kutoka kushoto kwenda kulia. Shughuli hizi zina kipaumbele sawa.
- Mabano na Alama Zingine za Kundi
- Jinsi ya kuchanganya maneno kama hayo.
- Tambua maneno kama hayo.
- Panga upya maneno ili kama maneno ni pamoja.
- Kuongeza au Ondoa coefficients na kuweka variable sawa kwa kila kundi la maneno kama.
Operesheni Maneno Ufafanuzi Ongezeko \(a\)pamoja \(b\)
na jumla ya \(a\)na \(b\)
\(a\)kuongezeka kwa \(b\)
\(b\)zaidi ya\(a\)
jumla ya \(a\)na \(b\)
\(b\)aliongeza kwa\(a\)\(a+b\) Kutoa \(a\)minus tofauti \(b\)
ya\(a\) na \(b\)
\(a\)ilipungua kwa \(b\)
\(b\)chini ya\(a\)
\(b\)imetolewa kutoka\(a\)\(a−b\) Kuzidisha \(a\)mara bidhaa \(b\)
ya \(a\)na \(b\)
mara mbili\(a\)\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\)
Idara \(a\)kugawanywa na \(b\)
quotient ya \(a\)na \(b\)
uwiano wa \(a\)na \(b\)
\(b\)imegawanywa\(a\)\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\)
faharasa
- mgawo
- Mgawo wa neno ni mara kwa mara ambayo huzidisha kutofautiana kwa muda.
- idadi ya vipengele
- Nambari ya composite ni namba ya kuhesabu ambayo si mkuu. Ina mambo mengine zaidi ya 1 na idadi yenyewe.
- mara kwa mara
- Mara kwa mara ni namba ambayo thamani yake daima inakaa sawa.
- kugawanyika kwa idadi
- Kama idadi \(m\)ni nyingi ya \(n\), basi \(m\)ni mgawanyiko na \(n\).
- mlinganyo
- Equation ni maneno mawili yanayounganishwa na ishara sawa.
- tathmini ya kujieleza
- Kutathmini kujieleza ina maana ya kupata thamani ya kujieleza wakati vigezo ni kubadilishwa na idadi fulani.
- kujieleza
- Maneno ni namba, kutofautiana, au mchanganyiko wa namba na vigezo kwa kutumia alama za uendeshaji.
- mambo
- Ikiwa\(a·b=m\), basi \(a\)na \(b\)ni sababu za \(m\).
- angalau ya kawaida nyingi
- Nyingi ya kawaida (LCM) ya namba mbili ni idadi ndogo zaidi ambayo ni nyingi ya namba zote mbili.
- kama maneno
- Masharti ambayo ni ama constants au kuwa na vigezo sawa kukulia kwa nguvu sawa ni kuitwa kama maneno.
- nyingi ya idadi
- idadi ni nyingi ya \(n\)kama ni bidhaa ya idadi kuhesabu na \(n\).
- utaratibu wa shughuli
- Utaratibu wa shughuli ni miongozo imara ya kurahisisha kujieleza.
- factorization mkuu
- Factorization mkuu wa idadi ni bidhaa ya idadi ya mkuu ambayo ni sawa na idadi.
- nambari kuu
- Nambari kuu ni namba ya kuhesabu zaidi ya 1 ambayo sababu zake pekee ni 1 na namba yenyewe.
- kurahisisha kujieleza
- Kurahisisha kujieleza ina maana ya kufanya hesabu yote iwezekanavyo.
- kipindi
- Neno ni mara kwa mara, au bidhaa ya vigezo vya mara kwa mara na moja au zaidi.
- kutofautisha
- Variable ni barua inayowakilisha namba ambayo thamani yake inaweza kubadilika.


