8.7: Equações paramétricas - Gráficos
- Page ID
- 189138
- Faça um gráfico de curvas planas descritas por equações paramétricas traçando pontos.
- Representar graficamente equações paramétricas.
É o final da nona entrada, com duas eliminações e dois homens na base. O time da casa está perdendo por duas corridas. O batedor balança e bate na bola a\(140\) pés por segundo e em um ângulo aproximado em relação\(45°\) à horizontal. Até onde a bola vai viajar? Isso abrirá a barreira para um home run vencedor do jogo? O resultado pode depender parcialmente de outros fatores (por exemplo, o vento), mas os matemáticos podem modelar o caminho de um projétil e prever aproximadamente até onde ele viajará usando equações paramétricas. Nesta seção, discutiremos equações paramétricas e algumas aplicações comuns, como problemas de movimento de projéteis.

Figura\(\PageIndex{1}\): Equações paramétricas podem modelar o caminho de um projétil. (crédito: Paul Kreher, Flickr)
Representação gráfica de equações paramétricas traçando pontos
Em vez de uma calculadora gráfica ou de um programa de computação gráfica, traçar pontos para representar o gráfico de uma equação é o método padrão. Desde que tenhamos cuidado ao calcular os valores, a plotagem de pontos é altamente confiável.
- Crie uma tabela com três colunas:\(t\)\(x(t)\),\(y(t)\) e.
- Avalie\(x\) e\(y\) para valores de tt no intervalo para o qual as funções são definidas.
- Faça um gráfico dos pares resultantes\((x,y)\).
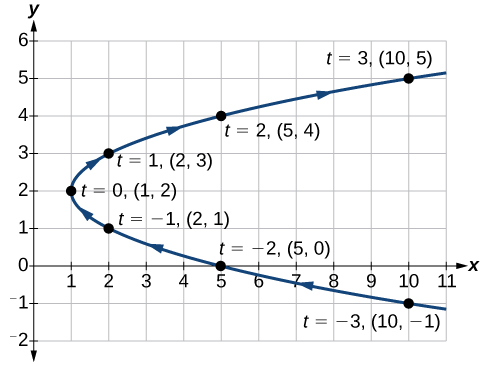
Esboce o gráfico das equações paramétricas\(x(t)=t^2+1\),\( y(t)=2+t\).
Solução
Construa uma tabela de valores para\(t\), e\(x(t)\)\(y(t)\), como em Tabela\(\PageIndex{1}\), e plote os pontos em um plano.
| \(t\) | \(x(t)=t^2+1\) | \(y(t)=2+t\) |
|---|---|---|
| \(−5\) | \(26\) | \(−3\) |
| \(−4\) | \(17\) | \(−2\) |
| \(−3\) | \(10\) | \(−1\) |
| \(−2\) | \(5\) | \(0\) |
| \(−1\) | \(2\) | \(1\) |
| \(0\) | \(1\) | \(2\) |
| \(1\) | \(2\) | \(3\) |
| \(2\) | \(5\) | \(4\) |
| \(3\) | \(10\) | \(5\) |
| \(4\) | \(17\) | \(6\) |
| \(5\) | \(26\) | \(7\) |
O gráfico é uma parábola com vértice no ponto\((1,2)\), abrindo para a direita. Veja a Figura\(\PageIndex{2}\).
Figura\(\PageIndex{2}\)
Análise
Como valores para o\(t\) progresso em uma direção positiva de\(0\) para\(5\), os pontos traçados traçam a metade superior da parábola. Como os valores geralmente se tornam negativos, eles traçam a metade inferior da parábola. Não há restrições no domínio. As setas indicam a direção de acordo com os valores crescentes de\(t\). O gráfico não representa uma função, pois falhará no teste da linha vertical. O gráfico é desenhado em duas partes: os valores positivos para\(t\) e os valores negativos para\(t\).
Esboce o gráfico das equações paramétricas\(x=\sqrt{t}\),\( y=2t+3\),\(0≤t≤3\).
- Resposta
-
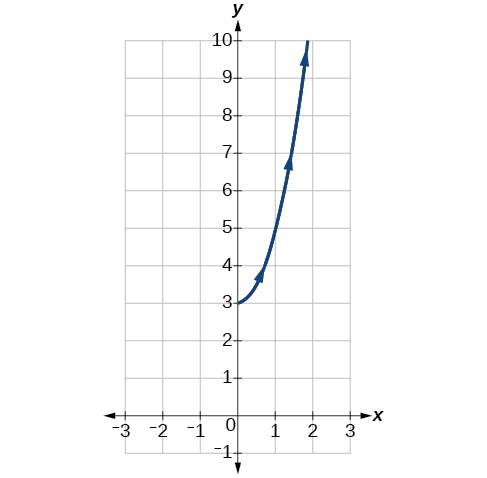
Figura\(\PageIndex{3}\)
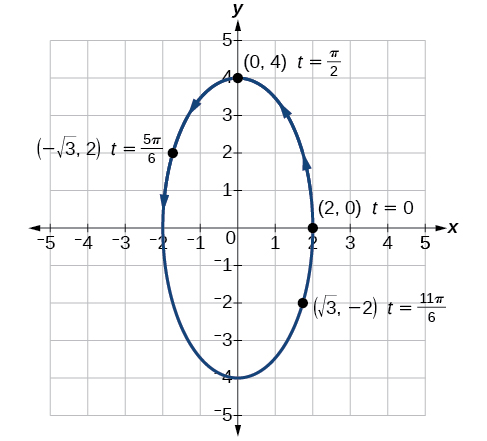
Crie uma tabela de valores para as equações paramétricas fornecidas e esboce o gráfico:
\(x=2 \cos t\)
\(y=4 \sin t\)
Solução
Construa uma tabela como essa na Tabela\(\PageIndex{2}\) usando a medida do ângulo em radianos como entradas para\(t\), e avaliando\(x\)\(y\) e. Usar ângulos com valores de seno e cosseno conhecidos para\(t\) facilita os cálculos.
| \(t\) | \(x=2 \cos t\) | \(y=4 \sin t\) |
|---|---|---|
| \(0\) | \(x=2 \cos(0)=2\) | \(y=4 \sin(0)=0\) |
| \(\dfrac{\pi}{6}\) | \(x=2 \cos(\dfrac{\pi}{6})=\sqrt{3}\) | \(y=4 \sin(\dfrac{π}{6})=2\) |
| \(\dfrac{\pi}{3}\) | \(x=2 \cos(\dfrac{\pi}{3})=1\) | \(y=4 \sin(\dfrac{\pi}{3})=2\sqrt{3}\) |
| \(\dfrac{\pi}{2}\) | \(x=2 \cos(\dfrac{\pi}{2})=0\) | \(y=4 \sin(\dfrac{\pi}{2})=4\) |
| \(\dfrac{2\pi}{3}\) | \(x=2 \cos(\dfrac{2\pi}{3})=−1\) | \(y=4 \sin(\dfrac{2\pi}{3})=2\sqrt{3}\) |
| \(\dfrac{5\pi}{6}\) | \(x=2 \cos(\dfrac{5\pi}{6})=−\sqrt{3}\) | \(y=4 \sin(\dfrac{5\pi}{6})=2\) |
| \(\pi\) | \(x=2 \cos(\pi)=−2\) | \(y=4 \sin(\pi)=0\) |
| \(\dfrac{7\pi}{6}\) | \(x=2 \cos(\dfrac{7\pi}{6})=−\sqrt{3}\) | \(y=4 \sin(\dfrac{7\pi}{6})=−2\) |
| \(\dfrac{4\pi}{3}\) | \(x=2 \cos(\dfrac{4\pi}{3})=−1\) | \(y=4 \sin(\dfrac{4\pi}{3})=−2\sqrt{3}\) |
| \(\dfrac{3\pi}{2}\) | \(x=2 \cos(\dfrac{3\pi}{2})=0\) | \(y=4 \sin(\dfrac{3\pi}{2})=−4\) |
| \(\dfrac{5\pi}{3}\) | \(x=2 \cos(\dfrac{5\pi}{3})=1\) | \(y=4 \sin(\dfrac{5\pi}{3})=−2\sqrt{3}\) |
| \(\dfrac{11\pi}{6}\) | \(x=2 \cos(\dfrac{11\pi}{6})=\sqrt{3}\) | \(y=4 \sin(\dfrac{11\pi}{6})=−2\) |
| \(2\pi\) | \(x=2 \cos(2\pi)=2\) | \(y=4 \sin(2\pi)=0\) |
A figura\(\PageIndex{4}\) mostra o gráfico.
Figura\(\PageIndex{4}\)
Pela simetria mostrada nos valores de\(x\) e\(y\), vemos que as equações paramétricas representam uma elipse. A elipse é mapeada no sentido anti-horário, conforme mostrado pelas setas que indicam\(t\) valores crescentes.
Análise
Vimos que equações paramétricas podem ser representadas graficamente traçando pontos. No entanto, uma calculadora gráfica economizará algum tempo e revelará nuances em um gráfico que podem ser entediantes demais para serem descobertas usando apenas cálculos manuais. Certifique-se de alterar o modo na calculadora para paramétrico (PAR). Para confirmar, a\(Y=\) janela deve mostrar
\[\begin{align*} X_{1T} &= \\ Y_{1T} &= \end{align*}\]
em vez de\(Y_1=\).
Representar graficamente as equações paramétricas:\(x=5 \cos t\),\(y=3 \sin t\).
- Resposta
-
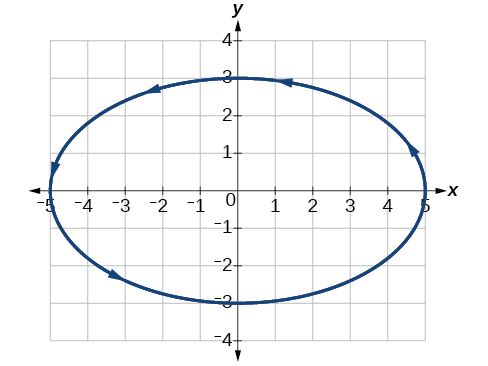
Figura\(\PageIndex{5}\)
Faça um gráfico das equações paramétricas\(x=5 \cos t\)\(y=2 \sin t\) e. Primeiro, construa o gráfico usando pontos de dados gerados a partir do formulário paramétrico. Em seguida, faça um gráfico da forma retangular da equação. Compare os dois gráficos.
Solução
Crie uma tabela de valores como essa na Tabela\(\PageIndex{3}\).
| \(t\) | \(x=5 \cos t\) | \(y=2 \sin t\) |
|---|---|---|
| \(0\) | \(x=5 \cos(0)=5\) | \(y=2 \sin(0)=0\) |
| \(1\) | \(x=5 \cos(1)≈2.7\) | \(y=2 \sin(1)≈1.7\) |
| \(2\) | \(x=5 \cos(2)≈−2.1\) | \(y=2 \sin(2)≈1.8\) |
| \(3\) | \(x=5 \cos(3)≈−4.95\) | \(y=2 \sin(3)≈0.28\) |
| \(4\) | \(x=5 \cos(4)≈−3.3\) | \(y=2 \sin(4)≈−1.5\) |
| \(5\) | \(x=5 \cos(5)≈1.4\) | \(y=2 \sin(5)≈−1.9\) |
| \(−1\) | \(x=5 \cos(−1)≈2.7\) | \(y=2 \sin(−1)≈−1.7\) |
| \(−2\) | \(x=5 \cos(−2)≈−2.1\) | \(y=2 \sin(−2)≈−1.8\) |
| \(−3\) | \(x=5 \cos(−3)≈−4.95\) | \(y=2 \sin(−3)≈−0.28\) |
| \(−4\) | \(x=5 \cos(−4)≈−3.3\) | \(y=2 \sin(−4)≈1.5\) |
| \(−5\) | \(x=5 \cos(−5)≈1.4\) | \(y=2 \sin(−5)≈1.9\) |
Faça um gráfico dos\((x,y)\) valores da tabela (Figura\(\PageIndex{6}\)).
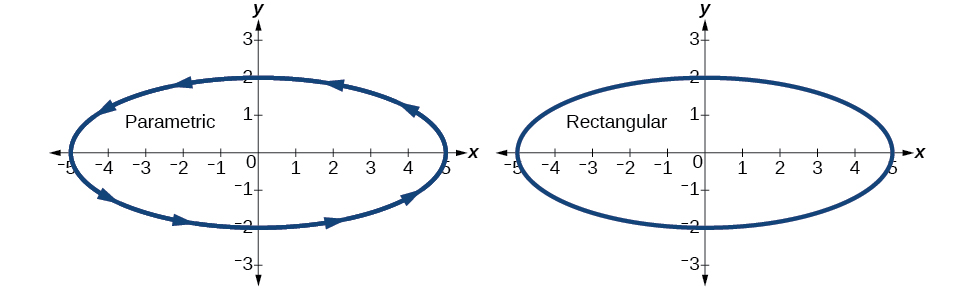
Figura\(\PageIndex{6}\)
Em seguida, traduza as equações paramétricas para a forma retangular. Para fazer isso, resolvemos por\(t\) em\(x(t)\) ou e\(y(t)\), em seguida, substituímos a expressão por\(t\) na outra equação. O resultado será uma função\(y(x)\) se resolver para\(t\) como uma função de\(x\), ou\(x(y)\) se resolver para\(t\) como uma função de\(y\).
\[\begin{align*} x &= 5 \cos t \\ \dfrac{x}{5} &= \cos t \end{align*}\]
Resolva para\(\cos t\).
\(y=2 \sin t\)
Resolva para\(\sin t\).
\(\dfrac{y}{2}=\sin t\)
Em seguida, use o Teorema de Pitágoras.
\[\begin{align*} {\cos}^2 t+{\sin}^2 t &=1 \\ {\left(\dfrac{x}{5}\right)}^2+{\left(\dfrac{y}{2}\right)}^2 &= 1 \\ \dfrac{x^2}{25}+\dfrac{y^2}{4} &=1 \end{align*}\]
Análise
Na Figura\(\PageIndex{7}\), os dados das equações paramétricas e da equação retangular são plotados juntos. As equações paramétricas são plotadas em azul; o gráfico da equação retangular é desenhado sobre a paramétrica em um estilo tracejado colorido em vermelho. Claramente, ambas as formas produzem o mesmo gráfico.
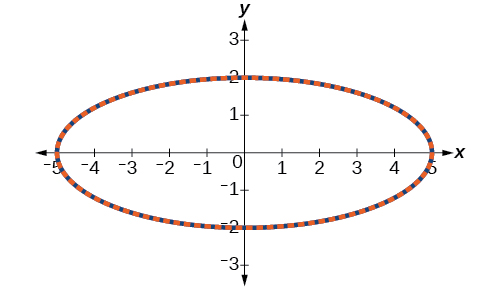
Figura\(\PageIndex{7}\)
Faça um gráfico das equações paramétricas\(x=t+1\) e\(y=\sqrt{t}\)\(t≥0\), e do equivalente retangular\(y=\sqrt{x−1}\) no mesmo sistema de coordenadas.
Solução
Construa uma tabela de valores para as equações paramétricas, como fizemos no exemplo anterior, e faça um gráfico\(y=\sqrt{t}\),\(t≥0\) na mesma grade, como na Figura\(\PageIndex{8}\).
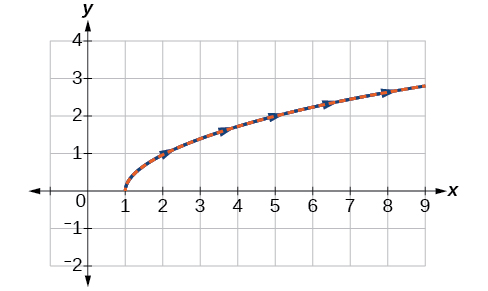
Figura\(\PageIndex{8}\)
Análise
Com o domínio\(t\) restrito, traçamos apenas valores positivos de\(t\). Os dados paramétricos são representados graficamente em azul e o gráfico da equação retangular é tracejado em vermelho. Mais uma vez, vemos que as duas formas se sobrepõem.
Esboce o gráfico das equações paramétricas\(x=2 \cos \theta\) e\(y=4 \sin \theta\), junto com a equação retangular, na mesma grade.
- Resposta
-
O gráfico das equações paramétricas está em vermelho e o gráfico da equação retangular é desenhado em pontos azuis sobre as equações paramétricas.
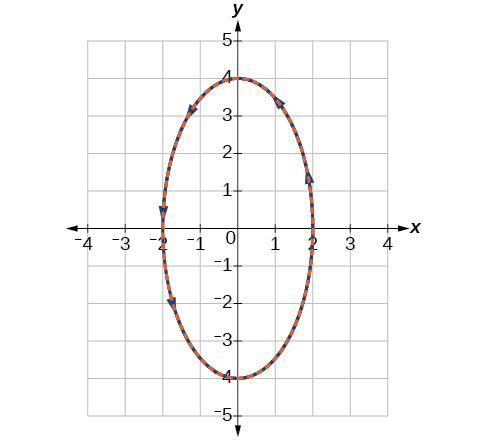
Figura\(\PageIndex{9}\)
Aplicações de equações paramétricas
Muitas das vantagens das equações paramétricas se tornam óbvias quando aplicadas à solução de problemas do mundo real. Embora as equações retangulares\(y\) forneçam uma visão geral do caminho de um objeto, elas não revelam a posição de um objeto em um momento específico.\(x\) As equações paramétricas, no entanto, ilustram como os valores\(x\) e\(y\) mudam dependendo\(t\) da localização de um objeto em movimento em um determinado momento.
Uma aplicação comum de equações paramétricas é resolver problemas envolvendo movimento de projéteis. Nesse tipo de movimento, um objeto é impulsionado para frente em uma direção ascendente formando um ângulo de em relação\(\theta\) à horizontal, com uma velocidade inicial de\(v_0\) e a uma altura\(h\) acima da horizontal.
O caminho de um objeto impulsionado em uma inclinação de\(\theta\) para a horizontal, com velocidade\(v_0\) inicial e a uma altura\(h\) acima da horizontal, é dado por
\[\begin{align*} x &= (v_0 \cos \theta)t \\ y &= −\dfrac{1}{2}gt^2+(v_0 \sin \theta)t+h \end{align*}\]
onde\(g\) explica os efeitos da gravidade e\(h\) é a altura inicial do objeto. Dependendo das unidades envolvidas no problema, use\(g=32 ft / s^2\) ou\(g=9.8 m / s^2\). A equação para\(x\) fornece a distância horizontal e a equação para\(y\) fornece a distância vertical.
- A distância horizontal é dada por\(x=(v_0 \cos \theta)t\). Substitua a velocidade inicial do objeto por\(v_0\).
- A expressão\(\cos \theta\) indica o ângulo no qual o objeto é impulsionado. Substitua esse ângulo em graus por\(\cos \theta\).
- A distância vertical é dada pela fórmula\(y=−\dfrac{1}{2}gt^2+(v_0 \sin \theta)t+h\). O termo\(−\dfrac{1}{2}gt^2\) representa o efeito da gravidade. Dependendo das unidades envolvidas, use\(g=32 ft/s^2\) ou\(g=9.8 m/s^2\). Novamente, substitua a\(v_0\) velocidade inicial e a altura na qual o objeto foi impulsionado\(h\).
- Prossiga calculando cada termo a ser resolvido\(t\).
Resolva o problema apresentado no início desta seção. O batedor acerta o home run vencedor do jogo? Suponha que a bola seja atingida com uma velocidade inicial de\(140\) pés por segundo em um ângulo em relação\(45°\) à horizontal, fazendo contato com\(3\) os pés acima do solo.
- Encontre as equações paramétricas para modelar o caminho da bola de beisebol.
- Onde está a bola depois de\(2\) alguns segundos?
- Quanto tempo a bola está no ar?
- É um home run?
Solução
1. Use as fórmulas para configurar as equações. A posição horizontal é encontrada usando a equação paramétrica para\(x\). Assim,
\[\begin{align*} x &= (v_0 \cos \theta)t \\ x &= (140 \cos(45°))t \end{align*}\]
A posição vertical é encontrada usando a equação paramétrica para\(y\). Assim,
\[\begin{align*} y &=−16t^2+(v_0 \sin \theta)t+h \\ y &= −16t^2+(140 \sin(45°))t+3 \end{align*}\]
2. Substitua\(2\) nas equações para encontrar as posições horizontal e vertical da bola.
\[\begin{align*} x &= (140 \cos(45°))(2) \\ x &= 198\space feet \\ y &= −16{(2)}^2+(140 \sin(45°))(2)+3 \\ y &=137\space feet \end{align*}\]
Depois de\(2\) segundos, a bola está a\(198\) pés da caixa do batedor e\(137\) pés acima do solo.
3. Para calcular quanto tempo a bola está no ar, precisamos descobrir quando ela atingirá o solo ou quando\(y=0\). Assim,
\[\begin{align*} y &= −16t^2+(140\sin(45∘))t+3 \\ y &=0 \text{ Set }y(t)=0 \text{ and solve the quadratic.} \\ t &= 6.2173 \end{align*}\]
Quando\(t=6.2173\) segundos, a bola atinge o chão. (A equação quadrática pode ser resolvida de várias maneiras, mas esse problema foi resolvido usando um programa de matemática de computador.)
4. Não podemos confirmar que a rebatida foi um home run sem considerar o tamanho do campo externo, que varia de campo para campo. No entanto, por uma questão de simplicidade, vamos supor que a parede externa esteja a poucos\(400\) metros da base, na parte mais profunda do parque. Vamos supor também que a parede tenha\(10\) pés de altura. Para determinar se a bola limpa a parede, precisamos calcular a altura da bola quando está em\(x = 400\) pés. Então, vamos definir\(x = 400\), resolver e inserir tt em\(y\).\(t\)
\[\begin{align*} x &= (140 \cos(45°))t \\ 400 &= (140 \cos(45°))t \\ t &= 4.04 \\ y &= −16{(4.04)}^2+(140 \sin(45°))(4.04)+3 \\ y &= 141.8 \end{align*}\]
A bola está com\(141.8\) pés no ar quando sai do estádio. Na verdade, foi um home run. Veja a Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\)
Acesse o seguinte recurso on-line para obter instruções e práticas adicionais com gráficos de equações paramétricas.
Conceitos-chave
- Quando há uma terceira variável, um terceiro parâmetro do qual\(y\) depende\(x\) e do qual depende, equações paramétricas podem ser usadas.
- Para representar graficamente equações paramétricas traçando pontos, crie uma tabela com três colunas rotuladas\(t\)\(x(t)\),\(y(t)\) e. Escolha valores para t em ordem crescente. Faça um gráfico das duas últimas colunas para\(x\)\(y\) e. Veja o exemplo\(\PageIndex{1}\) e o exemplo\(\PageIndex{2}\).
- Ao representar graficamente uma curva paramétrica traçando pontos, observe os valores t associados e mostre setas no gráfico indicando a orientação da curva. Veja o exemplo\(\PageIndex{3}\) e o exemplo\(\PageIndex{4}\).
- As equações paramétricas permitem que a direção ou a orientação da curva sejam mostradas no gráfico. Equações que não são funções podem ser representadas graficamente e usadas em muitas aplicações que envolvem movimento. Veja o exemplo\(\PageIndex{5}\).
- O movimento do projétil depende de duas equações paramétricas:\(x=(v_0 \cos \theta)t\)\(y=−16t^2+(v_0 \sin \theta)t+h\) e. A velocidade inicial é simbolizada como\(v_0\). \(\theta\)representa o ângulo inicial do objeto quando lançado e\(h\) representa a altura na qual o objeto é impulsionado.


