8.6: Equações paramétricas
- Page ID
- 189147
- Parametrize uma curva.
- Elimine o parâmetro.
- Encontre uma equação retangular para uma curva definida parametralmente.
- Encontre equações paramétricas para curvas definidas por equações retangulares.
Considere o caminho que uma lua segue ao orbitar um planeta, que gira simultaneamente em torno do sol, como visto na Figura\(\PageIndex{1}\). A qualquer momento, a lua está localizada em um ponto específico em relação ao planeta. Mas como escrevemos e resolvemos a equação para a posição da lua quando a distância do planeta, a velocidade da órbita da lua ao redor do planeta e a velocidade de rotação ao redor do sol são todas desconhecidas? Só podemos resolver para uma variável por vez.
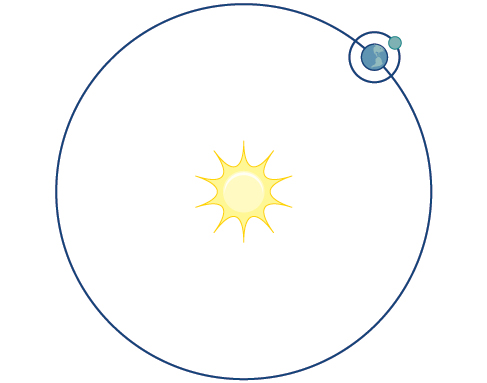
Nesta seção, consideraremos conjuntos de equações dados por\(x(t)\) e\(y(t)\) onde\(t\) está a variável independente do tempo. Podemos usar essas equações paramétricas em várias aplicações quando estamos procurando não apenas uma posição específica, mas também a direção do movimento. À medida que traçamos valores sucessivos de\(t\), a orientação da curva fica clara. Essa é uma das principais vantagens do uso de equações paramétricas: somos capazes de rastrear o movimento de um objeto ao longo de um caminho de acordo com o tempo. Começamos esta seção examinando os componentes básicos das equações paramétricas e o que significa parametrizar uma curva. Em seguida, aprenderemos como eliminar o parâmetro, traduzir as equações de uma curva definida parametricamente em equações retangulares e encontrar as equações paramétricas para curvas definidas por equações retangulares.
Parametrizando uma curva
Quando um objeto se move ao longo de uma curva — ou caminho curvilíneo — em uma determinada direção e em um determinado período de tempo, a posição do objeto no plano é dada pela coordenada\(x\) - e pela coordenada\(y\) -. No entanto, ambos\(x\)\(y\) variam ao longo do tempo, assim como as funções do tempo. Por esse motivo, adicionamos outra variável, o parâmetro, sobre o qual ambas\(x\) e\(y\) são funções dependentes. No exemplo do abridor de seção, o parâmetro é time,\(t\). A\(x\) posição da lua no tempo,\(t\), é representada como a função\(x(t)\), e a\(y\) posição da lua no tempo,\(t\), é representada como a função\(y(t)\). \(x(t)\)Juntos,\(y(t)\) são chamados de equações paramétricas e geram um par ordenado\((x(t), y(t))\). As equações paramétricas descrevem principalmente movimento e direção.
Quando parametrizamos uma curva, estamos traduzindo uma única equação em duas variáveis, como\(x\) e\(y\), em um par equivalente de equações em três variáveis\(x\)\(y\),,\(t\) e. Uma das razões pelas quais parametrizamos uma curva é porque as equações paramétricas fornecem mais informações: especificamente, a direção do movimento do objeto ao longo do tempo.
Quando representamos graficamente equações paramétricas, podemos observar os comportamentos individuais de\(x\) e de\(y\). Há várias formas que não podem ser representadas no formulário\(y=f(x)\), o que significa que elas não são funções. Por exemplo, considere o gráfico de um círculo, dado como\(r^2=x^2+y^2\). Resolução de\(y\) dados\(y=\pm \sqrt{r^2−x^2}\), ou duas equações:\(y_1=\sqrt{r^2−x^2}\)\(y_2=−\sqrt{r^2−x^2}\) e. Se representarmos graficamente\(y_1\) e\(y_2\) juntos, o gráfico não passará no teste da linha vertical, conforme mostrado na Figura\(\PageIndex{2}\). Assim, a equação para o gráfico de uma circunferência não é uma função.
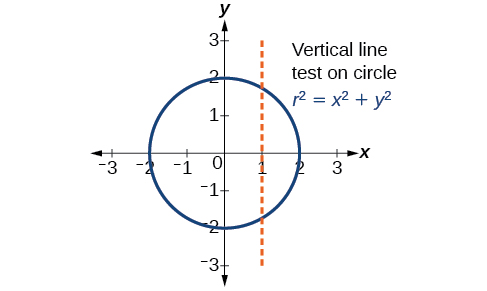
No entanto, se fôssemos representar graficamente cada equação sozinha, cada uma passaria no teste da linha vertical e, portanto, representaria uma função. Em alguns casos, o conceito de dividir a equação de um círculo em duas funções é semelhante ao conceito de criar equações paramétricas, pois usamos duas funções para produzir uma não função. Isso ficará mais claro à medida que avançarmos.
Suponha que\(t\) seja um número em um intervalo,\(I\). O conjunto de pares ordenados\((x(t), y(t))\), onde\(x=f(t)\) e\(y=g(t)\), forma uma curva plana com base no parâmetro\(t\). As equações\(x=f(t)\) e\(y=g(t)\) são as equações paramétricas.
Parametrize a curva\(y=x^2−1\) deixando\(x(t)=t\). Faça um gráfico das duas equações.
Solução
Se\(x(t)=t\), então, para encontrar,\(y(t)\) substituímos a variável\(x\) pela expressão dada em\(x(t)\). Em outras palavras,\(y(t)=t^2−1\) .Faça uma tabela de valores semelhante à Tabela\(\PageIndex{1}\) e desenhe o gráfico.
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t\) ">\(−4\) | \ (x (t)\) ">\(−4\) | \ (y (t)\) ">\(y(−4)={(−4)}^2−1=15\) |
| \ (t\) ">\(−3\) | \ (x (t)\) ">\(−3\) | \ (y (t)\) ">\(y(−3)={(−3)}^2−1=8\) |
| \ (t\) ">\(−2\) | \ (x (t)\) ">\(−2\) | \ (y (t)\) ">\(y(−2)={(−2)}^2−1=3\) |
| \ (t\) ">\(−1\) | \ (x (t)\) ">\(−1\) | \ (y (t)\) ">\(y(−1)={(−1)}^2−1=0\) |
| \ (t\) ">\(0\) | \ (x (t)\) ">\(0\) | \ (y (t)\) ">\(y(0)={(0)}^2−1=−1\) |
| \ (t\) ">\(1\) | \ (x (t)\) ">\(1\) | \ (y (t)\) ">\(y(1)={(1)}^2−1=0\) |
| \ (t\) ">\(2\) | \ (x (t)\) ">\(2\) | \ (y (t)\) ">\(y(2)={(2)}^2−1=3\) |
| \ (t\) ">\(3\) | \ (x (t)\) ">\(3\) | \ (y (t)\) ">\(y(3)={(3)}^2−1=8\) |
| \ (t\) ">\(4\) | \ (x (t)\) ">\(4\) | \ (y (t)\) ">\(y(4)={(4)}^2−1=15\) |
Veja os gráficos na Figura\(\PageIndex{3}\). Pode ser útil usar o recurso TRACE de uma calculadora gráfica para ver como os pontos são gerados como\(t\) aumentos.
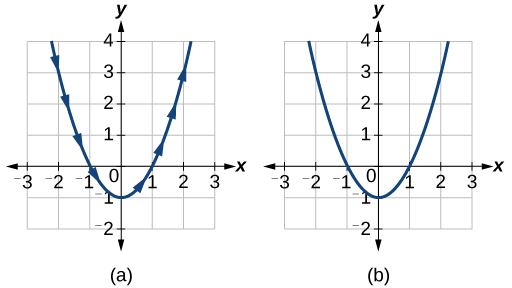
Análise
As setas indicam a direção na qual a curva é gerada. Observe que a curva é idêntica à curva de\(y=x^2−1\).
Construa uma tabela de valores e plote as equações paramétricas:\(x(t)=t−3\),\(y(t)=2t+4\);\(−1≤t≤2\).
- Responda
-
\(t\) \(x(t)\) \(y(t)\) \ (t\) ">\(-1\) \ (x (t)\) ">\(-4\) \ (y (t)\) ">\(2\) \ (t\) ">\(0\) \ (x (t)\) ">\(-3\) \ (y (t)\) ">\(4\) \ (t\) ">\(1\) \ (x (t)\) ">\(-2\) \ (y (t)\) ">\(6\) \ (t\) ">\(2\) \ (x (t)\) ">\(-1\) \ (y (t)\) ">\(8\) 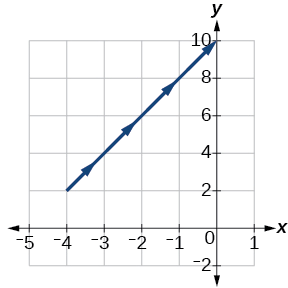
Figura\(\PageIndex{4}\)
Encontre um par de equações paramétricas que modelam o gráfico de\(y=1−x^2\), usando o parâmetro\(x(t)=t\). Faça um gráfico de alguns pontos e desenhe o gráfico.
Solução
Se\(x(t)=t\) e nós substituirmos\(t\) por\(x\) na\(y\) equação, então\(y(t)=1−t^2\). Nosso par de equações paramétricas é
\[\begin{align*} x(t) &=t \\ y(t) &= 1−t^2 \end{align*}\]
Para representar graficamente as equações, primeiro construímos uma tabela de valores como essa na Tabela\(\PageIndex{2}\). Podemos escolher valores ao redor\(t=0\), de\(t=−3\) até\(t=3\). Os valores na\(x(t)\) coluna serão os mesmos que os da\(t\) coluna porque\(x(t)=t\). Calcule valores para a coluna\(y(t)\).
| \ (t) | \(x(t)=t\) | \(y(t)=1−t^2\) |
|---|---|---|
| \ (t) ">\ (−3\) | \ (x (t) =t\) ">\(−3\) | \ (y (t) =1−t^2\) ">\(y(−3)=1−{(−3)}^2=−8\) |
| \ (t) ">\ (−2\) | \ (x (t) =t\) ">\(−2\) | \ (y (t) =1−t^2\) ">\(y(−2)=1−{(−2)}^2=−3\) |
| \ (t) ">\ (−1\) | \ (x (t) =t\) ">\(−1\) | \ (y (t) =1−t^2\) ">\(y(−1)=1−{(−1)}^2=0\) |
| \ (t) ">\ (0\) | \ (x (t) =t\) ">\(0\) | \ (y (t) =1−t^2\) ">\(y(0)=1−0=1\) |
| \ (t) ">\ (1\) | \ (x (t) =t\) ">\(1\) | \ (y (t) =1−t^2\) ">\(y(1)=1−{(1)}^2=0\) |
| \ (t) ">\ (2\) | \ (x (t) =t\) ">\(2\) | \ (y (t) =1−t^2\) ">\(y(2)=1−{(2)}^2=−3\) |
| \ (t) ">\ (3\) | \ (x (t) =t\) ">\(3\) | \ (y (t) =1−t^2\) ">\(y(3)=1−{(3)}^2=−8\) |
O gráfico de\(y=1−t^2\) é uma parábola voltada para baixo, conforme mostrado na Figura\(\PageIndex{5}\). Mapeamos a curva ao longo do intervalo\([−3, 3]\), mostrada como uma linha sólida com setas indicando a orientação da curva de acordo com\(t\). A orientação se refere ao caminho traçado ao longo da curva em termos de valores crescentes de\(t\). Como essa parábola é simétrica em relação à linha\(x=0\), os valores de\(x\) são refletidos no eixo y.
Parametrize a curva dada por\(x=y^3−2y\).
- Responda
-
\(x(t)=t^3−2t\)
\(y(t)=t\)
Um objeto viaja a uma taxa constante ao longo de um caminho reto\((−5, 3)\) até\((3, −1)\) o mesmo plano em quatro segundos. As coordenadas são medidas em metros. Encontre equações paramétricas para a posição do objeto.
Solução
As equações paramétricas são expressões lineares simples, mas precisamos ver esse problema passo a passo. O valor x do objeto começa em\(−5\) metros e vai para\(3\) metros. Isso significa que a distância\(x\) mudou em\(8\) metros em\(4\) segundos, que é uma taxa de\(\dfrac{8\space m}{4\space s}\), ou\(2\space m/s\). Podemos escrever a coordenada x como uma função linear em relação ao tempo como\(x(t)=2t−5\). No modelo de função linear\(y=mx+b\),\(2t=mx\)\(−5=b\) e.
Da mesma forma, o\(y\) valor -do objeto começa em\(3\) e vai para\(−1\), que é uma mudança na distância\(y\) de\(−4\) metros em\(4\) segundos, que é uma taxa de\(\dfrac{−4\space m}{4\space s}\), ou\(−1\space m/s\). Também podemos escrever a coordenada y como função linear\(y(t)=−t+3\). Juntas, essas são as equações paramétricas para a posição do objeto, onde\(x\) e\(y\) são expressas em metros e\(t\) representam o tempo:
\[\begin{align*} x(t) &= 2t−5 \\ y(t) &= −t+3 \end{align*}\]
Usando essas equações, podemos criar uma tabela de valores para\(t\)\(x\), e\(y\) (consulte a Tabela\(\PageIndex{3}\)). Neste exemplo, limitamos os valores de\(t\) a números não negativos. Em geral, qualquer valor de\(t\) pode ser usado.
| \(t\) | \(x(t)=2t−5\) | \(y(t)=−t+3\) |
|---|---|---|
| \ (t\) ">\(0\) | \ (x (t) =2t−5\) ">\(x=2(0)−5=−5\) | \ (y (t) =−t+3\) ">\(y=−(0)+3=3\) |
| \ (t\) ">\(1\) | \ (x (t) =2t−5\) ">\(x=2(1)−5=−3\) | \ (y (t) =−t+3\) ">\(y=−(1)+3=2\) |
| \ (t\) ">\(2\) | \ (x (t) =2t−5\) ">\(x=2(2)−5=−1\) | \ (y (t) =−t+3\) ">\(y=−(2)+3=1\) |
| \ (t\) ">\(3\) | \ (x (t) =2t−5\) ">\(x=2(3)−5=1\) | \ (y (t) =−t+3\) ">\(y=−(3)+3=0\) |
| \ (t\) ">\(4\) | \ (x (t) =2t−5\) ">\(x=2(4)−5=3\) | \ (y (t) =−t+3\) ">\(y=−(4)+3=−1\) |
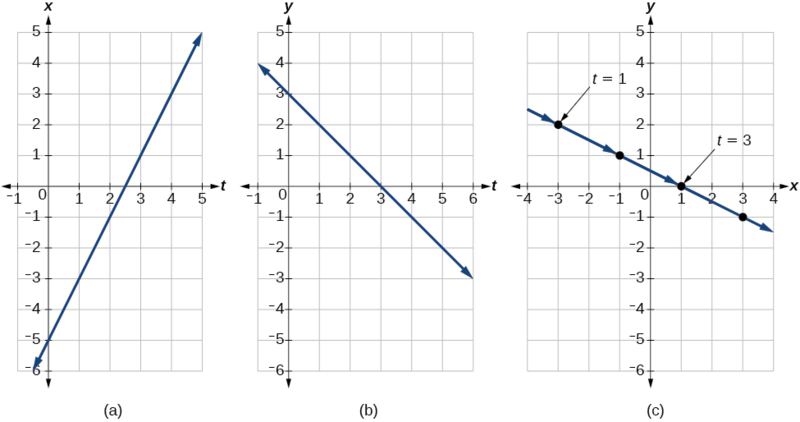
A partir dessa tabela, podemos criar três gráficos, conforme mostrado na Figura\(\PageIndex{6}\).
Análise
Novamente, vemos que, na Figura\(\PageIndex{6}\) (c), quando o parâmetro representa o tempo, podemos indicar o movimento do objeto ao longo do caminho com setas.
Eliminando o parâmetro
Em muitos casos, podemos ter um par de equações paramétricas, mas descobrimos que é mais simples desenhar uma curva se a equação envolver apenas duas variáveis, como\(x\)\(y\) e. A eliminação do parâmetro é um método que pode facilitar a representação gráfica de algumas curvas. No entanto, se estivermos preocupados com o mapeamento da equação de acordo com o tempo, será necessário indicar também a orientação da curva. Existem vários métodos para eliminar o parâmetro\(t\) de um conjunto de equações paramétricas; nem todo método funciona para todo tipo de equação. Aqui, revisaremos os métodos para os tipos mais comuns de equações.
Eliminando o parâmetro de equações polinomiais, exponenciais e logarítmicas
Para equações polinomiais, exponenciais ou logarítmicas expressas como duas equações paramétricas, escolhemos a equação que é mais facilmente manipulada e resolvida\(t\). Substituímos a expressão resultante por\(t\) na segunda equação. Isso fornece uma equação em\(x\)\(y\) e.
Dado\(x(t)=t^2+1\) e\(y(t)=2+t\), elimine o parâmetro e escreva as equações paramétricas como uma equação cartesiana.
Solução
Começaremos com a equação de\(y\) porque a equação linear é mais fácil de resolver\(t\).
\[\begin{align*} y &= 2+t \\ y−2 &=t \end{align*}\]
Em seguida, substitua\(y−2\) por\(t\) in\(x(t)\).
\[\begin{align*} x &= t^2+1 \\ x &= {(y−2)}^2+1 \;\;\;\;\;\;\;\; \text{Substitute the expression for }t \text{ into }x. \\ x &= y^2−4y+4+1 \\ x &= y^2−4y+5 \\ x &= y^2−4y+5 \end{align*}\]
A forma cartesiana é\(x=y^2−4y+5\).
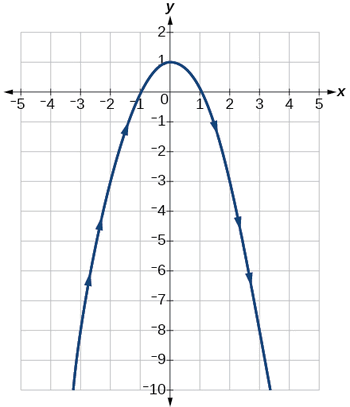
Análise
Essa é uma equação para uma parábola na qual, em termos retangulares,\(x\) depende de\(y\). Do vértice da curva em\((1,2)\), o gráfico se arrasta para a direita. Veja a Figura\(\PageIndex{7}\). Nesta seção, consideramos conjuntos de equações dados pelas funções\(x(t)\) e\(y(t)\), onde\(t\) está a variável independente do tempo. Observe, ambos\(x\) e\(y\) são funções do tempo; então, em geral, não\(y\) é uma função de\(x\).
Dadas as equações abaixo, elimine o parâmetro e escreva como uma equação retangular para\(y\) em função de\(x\).
\[\begin{align*} x(t) &= 2t^2+6 \\ y(t) &= 5−t \end{align*}\]
- Responda
-
\(y=5−\sqrt{\frac{1}{2}x−3}\)
Elimine o parâmetro e escreva como uma equação cartesiana:\(x(t)=e^{−t}\) e\(y(t)=3e^t\),\(t>0\).
Solução
Isolar\(e^t\).
\[\begin{align*} x &=e^{−t} \\ e^t &= \dfrac{1}{x} \end{align*}\]
Substitua a expressão em\(y(t)\).
\[\begin{align*} y &= 3e^t \\ y &= 3 \left(\dfrac{1}{x}\right) \\ y &= \dfrac{3}{x} \end{align*}\]
A forma cartesiana é\(y=\dfrac{3}{x}\).
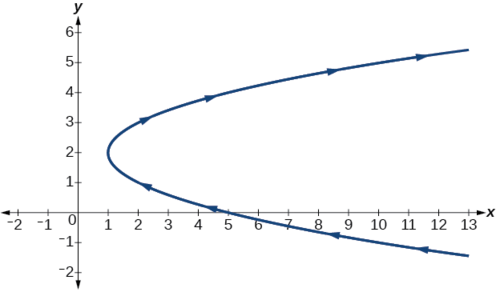
Análise
O gráfico da equação paramétrica é mostrado na Figura\(\PageIndex{8a}\). O domínio está restrito\(t>0\) a. A equação cartesiana,\(y=\dfrac{3}{x}\) é mostrada na Figura\(\PageIndex{8b}\) e tem apenas uma restrição no domínio,\(x≠0\).
Elimine o parâmetro e escreva como uma equação cartesiana:\(x(t)=\sqrt{t}+2\)\(y(t)=\log(t)\) e.
Solução
Resolva a primeira equação para\(t\).
\[\begin{align*} x &= \sqrt{t}+2 \\ x−2 &= \sqrt{t} \\ {(x−2)}^2 &= t \;\;\;\;\;\;\;\; \text{Square both sides.} \end{align*}\]
Em seguida, substitua a expressão por\(t\) na\(y\) equação.
\[\begin{align*} y &= \log(t) \\ y &= \log{(x−2)}^2 \end{align*}\]
A forma cartesiana é\(y=\log{(x−2)}^2\).
Análise
Para ter certeza de que as equações paramétricas são equivalentes à equação cartesiana, verifique os domínios. As equações paramétricas restringem o domínio\(x=\sqrt{t}+2\) a\(t>0\); nós restringimos o domínio\(x>2\) a.\(x\) O domínio da equação paramétrica\(y=\log(t)\) é restrito a\(t>0\); limitamos o domínio\(x>2\) a.\(y=\log{(x−2)}^2\)
Elimine o parâmetro e escreva como uma equação retangular.
\[\begin{align*} x(t) &= t^2 \\ y(t) &= \ln t\text{, } t>0 \end{align*}\]
- Responda
-
\(y=\ln \sqrt{x}\)
Eliminando o parâmetro das equações trigonométricas
A eliminação do parâmetro das equações trigonométricas é uma substituição direta. Podemos usar algumas das identidades trigonométricas familiares e o Teorema de Pitágoras.
Primeiro, usamos as identidades:
\[\begin{align*} x(t) &= a \cos t \\ y(t) &= b \sin t \end{align*}\]
Resolvendo para\(\cos t\) e\(\sin t\), temos
\[\begin{align*} \dfrac{x}{a} &= \cos t \\ \dfrac{y}{b} &= \sin t \end{align*}\]
Em seguida, use o Teorema de Pitágoras:
\({\cos}^2 t+{\sin}^2 t=1\)
Substituindo dá
\({\cos}^2 t+{\sin}^2 t={\left(\dfrac{x}{a}\right)}^2+{\left(\dfrac{y}{b}\right)}^2=1\)
Elimine o parâmetro de um determinado par de equações trigonométricas onde\(0≤t≤2\pi\) e esboce o gráfico.
\[\begin{align*} x(t) &=4 \cos t \\ y(t) &=3 \sin t \end{align*}\]
Solução
Resolvendo para\(\cos t\) e\(\sin t\), temos
\[\begin{align*} x &=4 \cos t \\ \dfrac{x}{4} &= \cos t \\ y &=3 \sin t \\ \dfrac{y}{3} &= \sin t \end{align*}\]
Em seguida, use a identidade pitagórica e faça as substituições.
\[\begin{align*} {\cos}^2 t+{\sin}^2 t &= 1 \\ {\left(\dfrac{x}{4}\right)}^2+{\left(\dfrac{y}{3}\right)}^2 &=1 \\ \dfrac{x^2}{16}+\dfrac{y^2}{9} &=1 \end{align*}\]
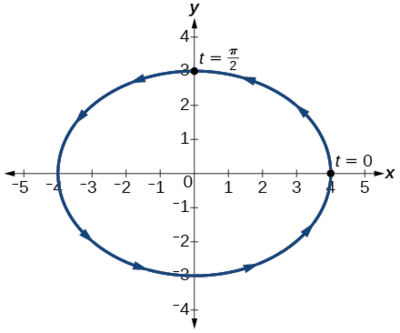
O gráfico da equação é mostrado na Figura\(\PageIndex{9}\).
Análise
Aplicando as equações gerais para seções cônicas (introduzidas na Geometria Analítica), podemos identificar\(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) como uma elipse centrada em\((0,0)\). Observe que quando\(t=0\) as coordenadas são\((4,0)\) e quando\(t=\dfrac{\pi}{2}\) as coordenadas são\((0,3)\). Isso mostra a orientação da curva com valores crescentes de\(t\).
Elimine o parâmetro de um determinado par de equações paramétricas e escreva como uma equação cartesiana:\(x(t)=2 \cos t\)\(y(t)=3 \sin t\) e.
- Responda
-
\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
Encontrando equações cartesianas a partir de curvas definidas parametricamente
Quando recebemos um conjunto de equações paramétricas e precisamos encontrar uma equação cartesiana equivalente, estamos essencialmente “eliminando o parâmetro”. No entanto, existem vários métodos que podemos usar para reescrever um conjunto de equações paramétricas como uma equação cartesiana. O método mais simples é definir uma equação igual ao parâmetro, como\(x(t)=t\). Nesse caso,\(y(t)\) pode ser qualquer expressão. Por exemplo, considere o seguinte par de equações.
\[\begin{align*} x(t) &=t \\ y(t) &= t^2−3 \end{align*}\]
Reescrever esse conjunto de equações paramétricas é uma questão\(x\) de substituir\(t\). Assim, a equação cartesiana é\(y=x^2−3\).
Use dois métodos diferentes para encontrar a equação cartesiana equivalente ao conjunto dado de equações paramétricas.
\[\begin{align*} x(t) &= 3t−2 \\ y(t) &= t+1 \end{align*}\]
Solução
Método 1. Primeiro, vamos resolver a\(x\) equação para\(t\). Então, podemos substituir o resultado na\(y\) equação.
\[\begin{align*} x &= 3t−2 \\ x+2 &= 3t \\ \dfrac{x+2}{3} &= t \end{align*}\]
Agora substitua a expressão por\(t\) na\(y\) equação.
\[\begin{align*} y &= t+1 \\ y & = \left(\dfrac{x+2}{3}\right)+1 \\ y &= \dfrac{x}{3}+\dfrac{2}{3}+1 \\ y &= \dfrac{1}{3}x+\dfrac{5}{3} \end{align*}\]
Método 2. Resolva a\(y\) equação\(t\) e substitua essa expressão na\(x\) equação.
\[\begin{align*} y &= t+1 \\ y−1 &=t \end{align*}\]
Faça a substituição e, em seguida, resolva por\(y\).
\[\begin{align*} x &= 3(y−1)−2 \\ x &= 3y−3−2 \\ x &= 3y−5 \\ x+5 &= 3y \\ \dfrac{x+5}{3} &= y \\ y &= \dfrac{1}{3}x+\dfrac{5}{3} \end{align*}\]
Escreva as equações paramétricas fornecidas como uma equação cartesiana:\(x(t)=t^3\)\(y(t)=t^6\) e.
- Responda
-
\(y=x^2\)
Encontrando equações paramétricas para curvas definidas por equações retangulares
Embora tenhamos acabado de mostrar que há apenas uma maneira de interpretar um conjunto de equações paramétricas como uma equação retangular, existem várias maneiras de interpretar uma equação retangular como um conjunto de equações paramétricas. Qualquer estratégia que possamos usar para encontrar as equações paramétricas é válida se produzir equivalência. Em outras palavras, se escolhermos uma expressão para representar\(x\) e depois substituí-la na\(y\) equação, e ela produzir o mesmo gráfico no mesmo domínio da equação retangular, o conjunto de equações paramétricas é válido. Se o domínio ficar restrito no conjunto de equações paramétricas e a função não permitir os mesmos valores do domínio da equação retangular, os gráficos serão diferentes.\(x\)
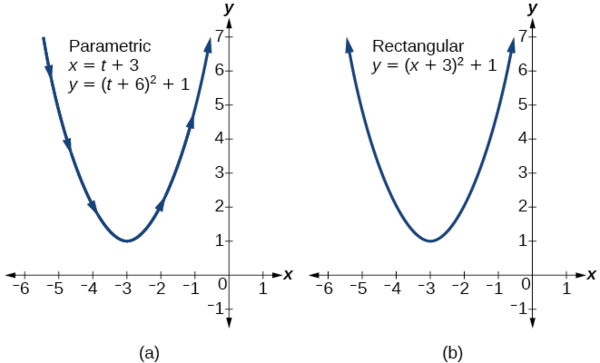
Encontre um conjunto de equações paramétricas equivalentes para\(y={(x+3)}^2+1\).
Solução
Uma escolha óbvia seria deixar\(x(t)=t\). Então\(y(t)={(t+3)}^2+1\). Mas vamos tentar algo mais interessante. E se deixarmos\(x=t+3\)? Então nós temos
\[\begin{align*} y &= {(x+3)}^2+1 \\ y &= {((t+3)+3)}^2+1 \\ y &= {(t+6)}^2+1 \end{align*}\]
O conjunto de equações paramétricas é
\[\begin{align*} x(t) &= t+3 \\ y(t) &= {(t+6)}^2+1 \end{align*}\]
Veja a Figura\(\PageIndex{10}\).
Acesse esses recursos on-line para obter instruções e práticas adicionais com equações paramétricas.
- Introdução às equações paramétricas
- Convertendo equações paramétricas em forma retangular
Conceitos chave
- Parametrizar uma curva envolve a tradução de uma equação retangular em duas variáveis\(x\) e\(y\), em duas equações em três variáveis\(x\)\(y\),,\(t\) e. Muitas vezes, mais informações são obtidas de um conjunto de equações paramétricas. Veja exemplo\(\PageIndex{1}\)\(\PageIndex{2}\), exemplo e exemplo\(\PageIndex{3}\).
- Às vezes, as equações são mais simples de representar graficamente quando escritas em forma retangular. Ao eliminar\(t\), uma equação em\(x\) e\(y\) é o resultado.
- Para eliminar\(t\), resolva uma das equações\(t\) e substitua a expressão na segunda equação. Veja exemplo\(\PageIndex{4}\), exemplo\(\PageIndex{5}\)\(\PageIndex{6}\), exemplo e exemplo\(\PageIndex{7}\).
- Encontrar a equação retangular para uma curva definida parametralmente é basicamente o mesmo que eliminar o parâmetro. Resolva para\(t\) em uma das equações e substitua a expressão na segunda equação. Veja o exemplo\(\PageIndex{8}\).
- Há um número infinito de maneiras de escolher um conjunto de equações paramétricas para uma curva definida como uma equação retangular.
- Encontre uma expressão para\(x\) que o domínio do conjunto de equações paramétricas permaneça o mesmo da equação retangular original. Veja o exemplo\(\PageIndex{9}\).


