8.8: Vetores
- Page ID
- 189167
- Visualize vetores geometricamente.
- Encontre magnitude e direção.
- Execute adição vetorial e multiplicação escalar.
- Encontre a forma do componente de um vetor.
- Encontre o vetor unitário na direção de\(v\).
- Execute operações com vetores em termos de\(i\)\(j\) e.
- Encontre o produto escalar de dois vetores.
Um avião está voando a uma velocidade aérea de\(200\) milhas por hora em direção a um rumo SE de\(140°\). Um vento norte (de norte a sul) está soprando\(16.2\) a milhas por hora, conforme mostrado na Figura\(\PageIndex{1}\). Quais são a velocidade do solo e o rumo real do avião?
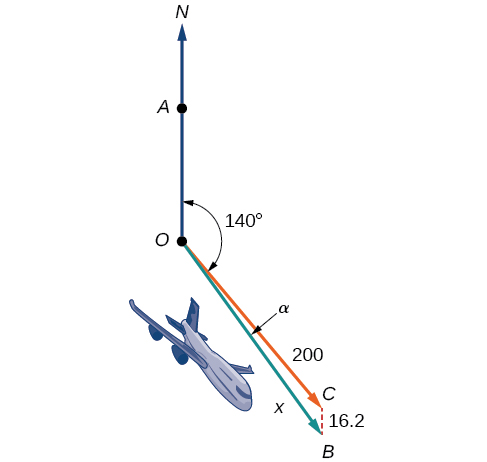
Figura\(\PageIndex{1}\)
A velocidade do solo se refere à velocidade de um avião em relação ao solo. A velocidade do ar se refere à velocidade que um avião pode viajar em relação à massa de ar circundante. Essas duas quantidades não são as mesmas por causa do efeito do vento. Em uma seção anterior, usamos triângulos para resolver um problema semelhante envolvendo o movimento de barcos. Mais adiante nesta seção, encontraremos a velocidade do solo e o rumo do avião, enquanto investigamos outra abordagem para problemas desse tipo. Primeiro, porém, vamos examinar os fundamentos dos vetores.
Uma visão geométrica dos vetores
Um vetor é uma quantidade específica desenhada como um segmento de linha com uma ponta de seta em uma extremidade. Tem um ponto inicial, onde começa, e um ponto terminal, onde termina. Um vetor é definido por sua magnitude, ou o comprimento da linha, e sua direção, indicada por uma ponta de seta no ponto terminal. Assim, um vetor é um segmento de linha direcionado. Existem vários símbolos que distinguem vetores de outras quantidades:
- Letras minúsculas, em negrito, com ou sem uma seta na parte superior \(u\), como\(w\),\(\overrightarrow{v}\),\(\overrightarrow{u}\),\(\overrightarrow{w}\).
- Dado o ponto inicial\(P\) e o ponto terminal\(Q\), um vetor pode ser representado como\(\overrightarrow{PQ}\). A ponta da seta na parte superior é o que indica que não é apenas uma linha, mas um segmento de linha direcionado.
- Dado um ponto inicial\((0,0)\) e um ponto terminal\((a,b)\), um vetor pode ser representado como\(⟨a,b⟩\).
Este último símbolo\(⟨a,b⟩\) tem um significado especial. É chamada de posição padrão. O vetor de posição tem um ponto inicial\((0,0)\) e um ponto terminal\(⟨a,b⟩\). Para transformar qualquer vetor no vetor de posição, pensamos na mudança nas coordenadas x e na mudança nas coordenadas y. Assim, se o ponto inicial de um vetor\(\overrightarrow{CD}\) for\(C(x_1,y_1)\) e o ponto terminal for\(D(x_2,y_2)\), o vetor de posição será encontrado calculando
\[\begin{align*} \overrightarrow{AB} &= ⟨x_2−x_1,y_2−y_1⟩ \\[4pt] &= ⟨a,b⟩ \end{align*}\]
Na Figura\(\PageIndex{2}\), vemos o vetor original\(\overrightarrow{CD}\) e o vetor de posição\(\overrightarrow{AB}\).
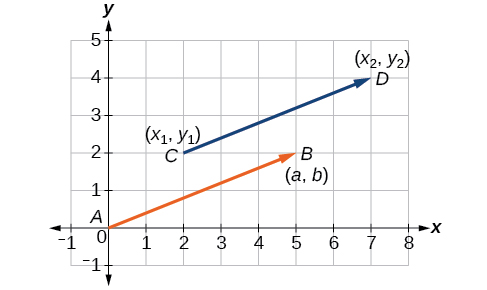
Figura\(\PageIndex{2}\)
Um vetor é um segmento de linha direcionado com um ponto inicial e um ponto terminal. Os vetores são identificados pela magnitude, ou pelo comprimento da linha e pela direção, representados pela ponta da seta apontando para o ponto terminal. O vetor de posição tem um ponto inicial em\((0,0)\) e é identificado por seu ponto terminal\(⟨a,b⟩\).
Considere o vetor cujo ponto inicial é\(P(2,3)\) e o ponto terminal é\(Q(6,4)\). Encontre o vetor de posição.
Solução
O vetor de posição é encontrado subtraindo uma\(x\) coordenada\(x\) -da outra coordenada\(y\) -e uma coordenada\(y\) -da outra coordenada. Assim
\[\begin{align*} v &= ⟨6−2,4−3⟩ \\[4pt] &=⟨4,1⟩ \end{align*}\]
O vetor de posição começa em\((0,0)\) e termina em\((4,1)\). Os gráficos de ambos os vetores são mostrados na Figura\(\PageIndex{3}\).
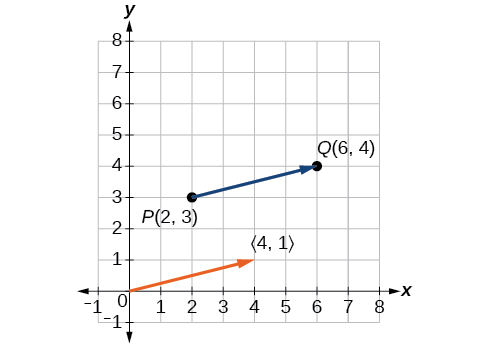
Figura\(\PageIndex{3}\)
Vemos que o vetor de posição é\(⟨4,1⟩\).
Encontre o vetor de posição, dado que o vetor\(v\) tem um ponto inicial em\((−3,2)\) e um ponto terminal em e\((4,5)\), em seguida, represente graficamente os dois vetores no mesmo plano.
Solução
O vetor de posição é encontrado usando o seguinte cálculo:
\[\begin{align*} v &= ⟨4−(−3),5−2⟩ \\[4pt] &= ⟨7,3⟩ \end{align*}\]
Assim, o vetor de posição começa em\((0,0)\) e termina em\((7,3)\). Veja a Figura\(\PageIndex{4}\).
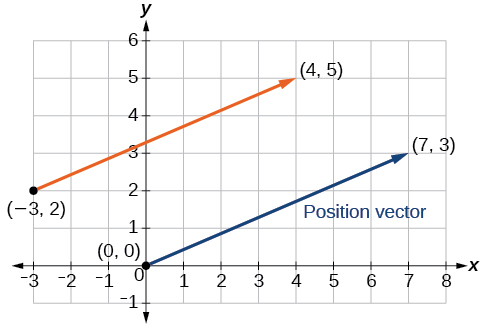
Figura\(\PageIndex{4}\)
Desenhe um vetor\(\vec{v}\) que se conecte da origem ao ponto\((3,5)\).
- Responda
-
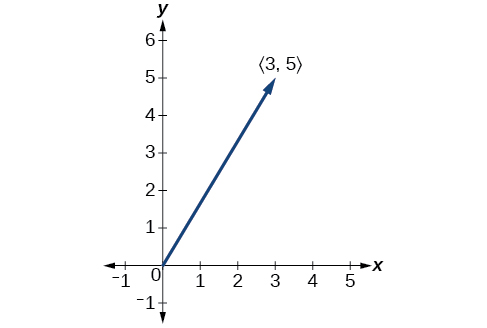
Figura\(\PageIndex{5}\)
Encontrando magnitude e direção
Para trabalhar com um vetor, precisamos ser capazes de encontrar sua magnitude e sua direção. Encontramos sua magnitude usando o Teorema de Pitágoras ou a fórmula da distância e encontramos sua direção usando a função tangente inversa.
Dado um vetor de posição\(\vec{v}=⟨a,b⟩\), a magnitude é encontrada por\(| v |=\sqrt{a^2+b^2}\) .A direção é igual ao ângulo formado com o\(x\) eixo -ou com o\(y\) eixo -, dependendo da aplicação. Para um vetor de posição, a direção é encontrada por\(\tan \theta=\left(\dfrac{b}{a}\right)⇒\theta={\tan}^{−1}\left(\dfrac{b}{a}\right)\), conforme ilustrado na Figura\(\PageIndex{6}\).
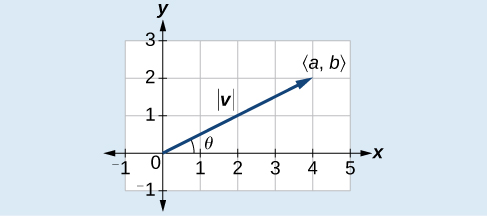
Figura\(\PageIndex{6}\)
Dois vetores\(\vec{v}\) e\(\vec{u}\) são considerados iguais se tiverem a mesma magnitude e a mesma direção. Além disso, se os dois vetores tiverem o mesmo vetor de posição, eles serão iguais.
Encontre a magnitude e a direção do vetor com o ponto inicial\(P(−8,1)\) e o ponto terminal\(Q(−2,−5)\). Desenhe o vetor.
Solução
Primeiro, encontre o vetor de posição.
\[\begin{align*} u &= ⟨−2,−(−8),−5−1⟩ \\[4pt] &= ⟨6,−6⟩ \end{align*}\]
Usamos o Teorema de Pitágoras para encontrar a magnitude.
\[\begin{align*} |u| &= \sqrt{{(6)}^2+{(−6)}^2} \\[4pt] &= \sqrt{72} \\[4pt] &=\sqrt{62} \end{align*}\]
A direção é dada como
\[\begin{align*} \tan \theta & =\dfrac{−6}{6}=−1\rightarrow \theta={\tan}^{−1}(−1) \\[4pt] &= −45° \end{align*}\]
No entanto, o ângulo termina no quarto quadrante, então adicionamos\(360°\) para obter um ângulo positivo. Assim,\(−45°+360°=315°\). Veja a Figura\(\PageIndex{7}\).
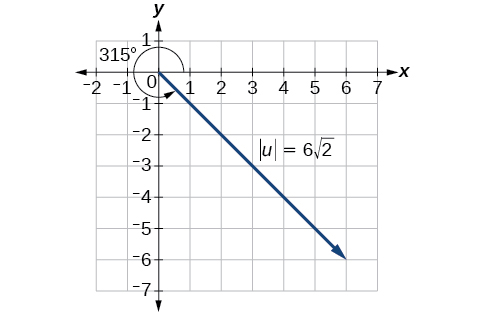
Figura\(\PageIndex{7}\)
Mostre que o vetor\(\vec{v}\) com ponto inicial em\((5,−3)\) e ponto terminal em\((−1,2)\) é igual ao vetor\(\vec{u}\) com ponto inicial em\((−1,−3)\) e ponto terminal em\((−7,2)\). Desenhe o vetor de posição na mesma grade que\(\vec{v}\)\(\vec{u}\) e. Em seguida, encontre a magnitude e a direção de cada vetor.
Solução
Conforme mostrado na Figura\(\PageIndex{8}\), desenhe o vetor\(\vec{v}\) começando no ponto inicial\((5,−3)\) e terminal\((−1,2)\). Desenhe o vetor\(\vec{u}\) com o ponto inicial\((−1,−3)\) e o ponto terminal\((−7,2)\). Encontre a posição padrão para cada um.
Em seguida, encontre e desenhe o vetor de posição para\(\vec{v}\)\(\vec{u}\) e. Nós temos
\[\begin{align*} v &= ⟨−1−5,2−(−3)⟩ \\[4pt] &= ⟨−6,5⟩u \\[4pt] &= ⟨−7−(−1),2−(−3)⟩ \\[4pt] & =⟨−6,5⟩ \end{align*}\]
Uma vez que os vetores de posição são os mesmos\(\vec{v}\) e\(\vec{u}\) são os mesmos.
Uma forma alternativa de verificar a igualdade vetorial é mostrar que a magnitude e a direção são as mesmas para os dois vetores. Para mostrar que as magnitudes são iguais, use o Teorema de Pitágoras.
\[\begin{align*} |v| &= \sqrt{{(−1−5)}^2+{(2−(−3))}^2} \\[4pt] &= \sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \\[4pt] |u| &= \sqrt{{(−7−(−1))}^2+{(2−(−3))}^2} \\[4pt] &=\sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \end{align*}\]
Como as magnitudes são iguais, agora precisamos verificar a direção. O uso da função tangente com o vetor de posição fornece
\[\begin{align*} \tan \theta &= −\dfrac{5}{6}⇒\theta={\tan}^{−1}\left(−\dfrac{5}{6}\right) \\[4pt] & = −39.8° \end{align*}\]
No entanto, podemos ver que o vetor de posição termina no segundo quadrante, então adicionamos\(180°\). Assim, a direção é\(−39.8°+180°=140.2°\).
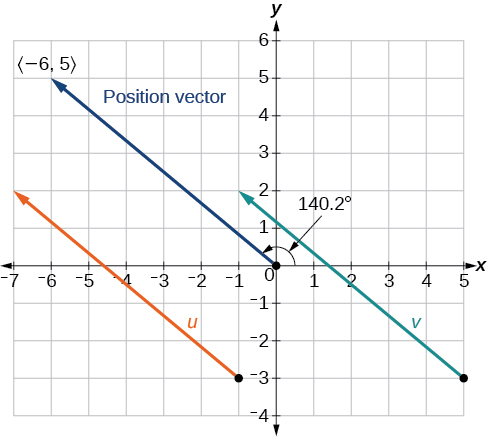
Figura\(\PageIndex{8}\)
Executando adição vetorial e multiplicação escalar
Agora que entendemos as propriedades dos vetores, podemos realizar operações envolvendo eles. Embora seja conveniente pensar no vetor\(u=⟨x,y⟩\) como uma seta ou um segmento de linha direcionado da origem ao ponto\((x,y)\), os vetores podem estar situados em qualquer lugar do plano. A soma de dois vetores\(\vec{u}\) e\(\vec{v}\), ou adição de vetor, produz um terceiro vetor\(\overrightarrow{u+ v}\), o vetor resultante.
Para encontrar\(\overrightarrow{u + v}\), primeiro desenhamos o vetor e\(\vec{u}\), a partir da extremidade terminal de\(\vec{u}\), desenhamos o vetor\(\vec{v}\). Em outras palavras, temos o ponto inicial de\(\vec{v}\) encontrar a extremidade terminal de\(\vec{u}\). Essa posição corresponde à noção de que nos movemos ao longo do primeiro vetor e, a partir de seu ponto terminal, nos movemos ao longo do segundo vetor. A soma\(\overrightarrow{u + v}\) é o vetor resultante porque resulta da adição ou subtração de dois vetores. O vetor resultante viaja diretamente do início\(\vec{u}\) ao fim de\(\vec{v}\) em um caminho reto, conforme mostrado na Figura\(\PageIndex{9}\).
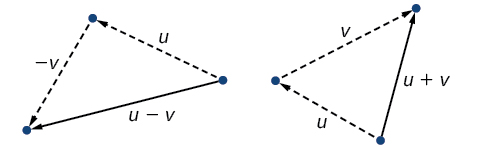
Figura\(\PageIndex{9}\)
A subtração vetorial é semelhante à adição vetorial. Para encontrar\(\overrightarrow{u − v}\), veja como\(\overrightarrow{u + (−v)}\). Adicionar\(\overrightarrow{−v}\) é inverter a direção de\(\vec{v}\) e adicioná-la ao final de\(\vec{u}\). O novo vetor começa no início de\(\vec{u}\) e para no ponto final de\(\overrightarrow{−v}\). Veja a Figura\(\PageIndex{10}\) para obter um visual que compara a adição e a subtração vetorial usando paralelogramos.
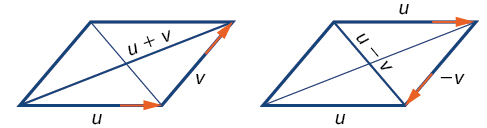
Figura\(\PageIndex{10}\)
Dado\(u=⟨3,−2⟩\) e\(v=⟨−1,4⟩\), encontre dois novos vetores\(\overrightarrow{u + v}\),\(\overrightarrow{u − v}\) e.
Solução
Para encontrar a soma de dois vetores, adicionamos os componentes. Assim,
\[ \begin{align*} u+v &= ⟨3,−2⟩+⟨−1,4⟩ \\[4pt] &= ⟨3+(−1),−2+4⟩ \\[4pt] &=⟨2,2⟩ \end{align*}\]
Veja a Figura\(\PageIndex{11a}\).
Para encontrar a diferença de dois vetores, adicione os componentes negativos\(\vec{v}\) de\(\vec{u}\) a. Assim,
\[\begin{align*}u+(−v) &=⟨3,−2⟩+⟨1,−4⟩ \\[4pt] &= ⟨3+1,−2+(−4)⟩ \\[4pt] &= ⟨4,−6⟩ \end{align*}\]
Veja a Figura\(\PageIndex{11b}\).
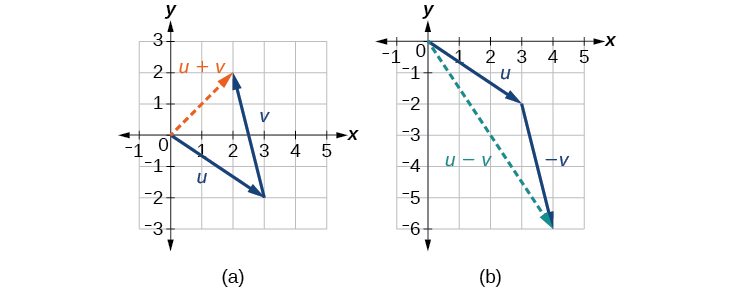
Figura\(\PageIndex{11}\): (a) Soma de dois vetores (b) Diferença de dois vetores
Multiplicação por um escalar
Enquanto adicionar e subtrair vetores nos dá um novo vetor com uma magnitude e direção diferentes, o processo de multiplicar um vetor por um escalar, uma constante, altera apenas a magnitude do vetor ou o comprimento da linha. A multiplicação escalar não tem efeito na direção, a menos que o escalar seja negativo. Nesse caso, a direção do vetor resultante é oposta à direção do vetor original.
A multiplicação escalar envolve o produto de um vetor e um escalar. Cada componente do vetor é multiplicado pelo escalar. Assim, para multiplicar\(v=⟨a,b⟩\) por\(k\), temos
\(kv=⟨ka,kb⟩\)
Somente a magnitude muda, a menos que\(k\) seja negativa, e então o vetor inverte a direção.
Dado vetor \(\vec{v}=⟨3,1⟩\)\(3\vec{v}\), encontre\(\dfrac{1}{2}\),\(\vec{−v}\) e.
Solução
Veja a Figura\(\PageIndex{12}\) para uma interpretação geométrica. Se\(\vec{v}=⟨3,1⟩\), então
\[\begin{align*} 3v &= ⟨3⋅3,3⋅1⟩ \\[4pt] &= ⟨9,3⟩ \\[4pt] \dfrac{1}{2}v &= ⟨\dfrac{1}{2}⋅3,\dfrac{1}{2}⋅1⟩ \\[4pt] &=⟨\dfrac{3}{2},\dfrac{1}{2}⟩ \\[4pt] −v &=⟨−3,−1⟩ \end{align*}\]
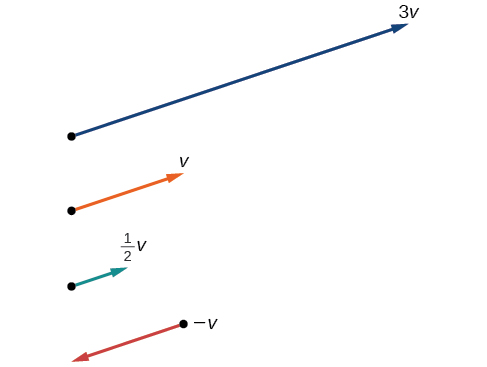
Figura\(\PageIndex{12}\)
Análise
Observe que o vetor\(3\vec{v}\) tem três vezes o comprimento de\(\vec{v}\),\(\dfrac{1}{2}\vec{v}\) é metade do\(\vec{v}\) comprimento e\(\overrightarrow{–v}\) tem o mesmo comprimento de\(\vec{v}\), mas na direção oposta.
Encontre o múltiplo escalar\(3u\) fornecido\(\vec{u}=⟨5,4⟩\).
- Responda
-
\(3u=⟨15,12⟩\)
Encontre uma equação linear para resolver as seguintes quantidades desconhecidas: Um número excede outro número em\(17\) e sua soma é\(31\). Encontre os dois números.
Solução
Primeiro, devemos multiplicar cada vetor pelo escalar.
\[\begin{align*} 3u &= 3⟨3,−2⟩ \\[4pt] &= ⟨9,−6⟩ \\[4pt] 2v &= 2⟨−1,4⟩ \\[4pt] &= ⟨−2,8⟩ \end{align*}\]
Em seguida, adicione os dois.
\[\begin{align*} w &= 3u+2v \\[4pt] &=⟨9,−6⟩+⟨−2,8⟩ \\[4pt] &= ⟨9−2,−6+8⟩ \\[4pt] &= ⟨7,2⟩ \end{align*}\]
Então,\(w=⟨7,2⟩\).
Encontrando o formulário de componente
Em algumas aplicações que envolvem vetores, é útil poder dividir um vetor em seus componentes. Os vetores são compostos por dois componentes: o componente horizontal é a\(x\) direção e o componente vertical é a\(y\) direção. Por exemplo, podemos ver no gráfico da Figura\(\PageIndex{13}\) que o vetor de posição\(⟨2,3⟩\) vem da adição dos vetores\(v_1\)\(v_2\) e. Temos\(v_2\) com ponto inicial\((0,0)\) e ponto terminal\((2,0)\).
\[\begin{align*} v_1 &= ⟨2−0,0−0⟩ \\[4pt] &= ⟨2,0⟩ \end{align*}\]
Também temos\(v_2\) com ponto inicial\((0,0)\) e ponto terminal\((0, 3)\).
\[\begin{align*} v_2 &= ⟨0−0,3−0⟩ \\[4pt] &= ⟨0,3⟩ \end{align*}\]
Portanto, o vetor de posição é
\[\begin{align*} v &= ⟨2+0,3+0⟩ \\[4pt] &= ⟨2,3⟩ \end{align*}\]
Usando o Teorema de Pitágoras, a magnitude de\(v_1\) é\(2\) e a magnitude de\(v_2\) é\(3\). Para encontrar a magnitude de\(v\), use a fórmula com o vetor de posição.
\[\begin{align*} |v| &= \sqrt{{|v_1|}^2+{|v_2|}^2} \\[4pt] &= \sqrt{2^2+3^2} \\[4pt] &= \sqrt{13} \end{align*}\]
A magnitude de\(v\) é\(\sqrt{13}\). Para encontrar a direção, usamos a função tangente\(\tan \theta=\dfrac{y}{x}\).
\[\begin{align*} \tan \theta &= \dfrac{v_2}{v_1} \\[4pt] \tan \theta &= \dfrac{3}{2} \\[4pt] \theta &={\tan}^{−1}\left(\dfrac{3}{2}\right)=56.3° \end{align*}\]
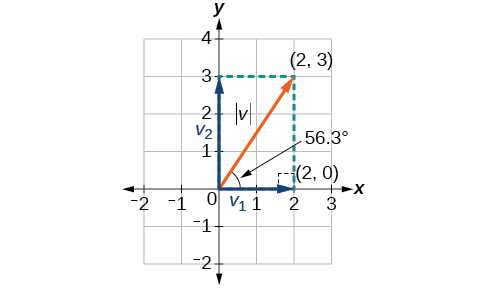
Figura\(\PageIndex{13}\)
Assim, a magnitude de\(\vec{v}\) é\(\sqrt{13}\) e a direção estão\(56.3^{\circ}\) fora da horizontal.
Encontre os componentes do vetor \(\vec{v}\)com o ponto inicial\((3,2)\) e o ponto terminal\((7,4)\).
Solução
Primeiro encontre a posição padrão.
\[\begin{align*} v &= ⟨7−3,4−2⟩ \\[4pt] &= ⟨4,2⟩ \end{align*}\]
Veja a ilustração na Figura\(\PageIndex{14}\).
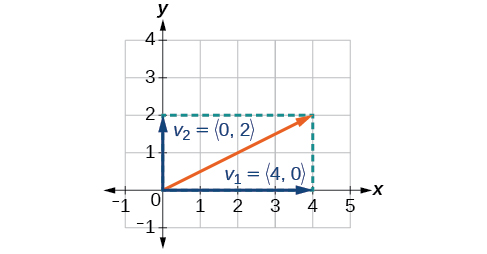
Figura\(\PageIndex{14}\)
O componente horizontal é\(\vec{v_1}=⟨4,0⟩\) e o componente vertical é\(\vec{v_2}=⟨0,2⟩\).
Encontrando o vetor unitário na direção de\(v\)
Além de encontrar os componentes de um vetor, também é útil na solução de problemas encontrar um vetor na mesma direção de um determinado vetor, mas de magnitude\(1\). Chamamos um vetor com a magnitude de\(1\) um vetor unitário. Podemos então preservar a direção do vetor original e, ao mesmo tempo, simplificar os cálculos.
Os vetores unitários são definidos em termos de componentes. O vetor unitário horizontal é escrito como\(\vec{i}=⟨1,0⟩\) e é direcionado ao longo do eixo horizontal positivo. O vetor unitário vertical é escrito como\(\vec{j}=⟨0,1⟩\) e é direcionado ao longo do eixo vertical positivo. Veja a Figura\(\PageIndex{15}\).
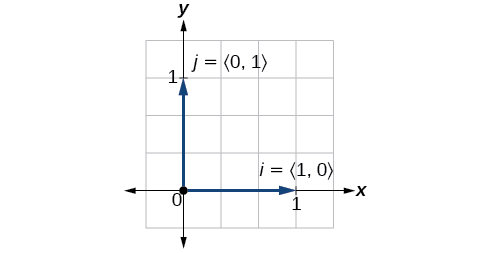
Figura\(\PageIndex{15}\)
Se \(\vec{v}\)for um vetor diferente de zero, então\(\dfrac{v}{| v |}\) é um vetor unitário na direção de \(v\). Qualquer vetor dividido por sua magnitude é um vetor unitário. Observe que a magnitude é sempre um escalar, e dividir por um escalar é o mesmo que multiplicar pelo inverso do escalar.
Encontre um vetor unitário na mesma direção que\(v=⟨−5,12⟩\).
Solução
Primeiro, descobriremos a magnitude.
\[\begin{align*} |v| &= \sqrt{{(−5)}^2+{(12)}^2} \\[4pt] &= \sqrt{25+144} \\[4pt] &=\sqrt{169} \\[4pt] &= 13 \end{align*}\]
Em seguida, dividimos cada componente por\(| v |\), o que fornece um vetor unitário na mesma direção que\(\vec{v}\):
\(\dfrac{v}{| v |} = −\dfrac{5}{13}i+\dfrac{12}{13}j \)
ou, em forma de componente
\(\dfrac{v}{| v |}= \left \langle -\dfrac{5}{13},\dfrac{12}{13} \right \rangle\)
Veja a Figura\(\PageIndex{16}\).
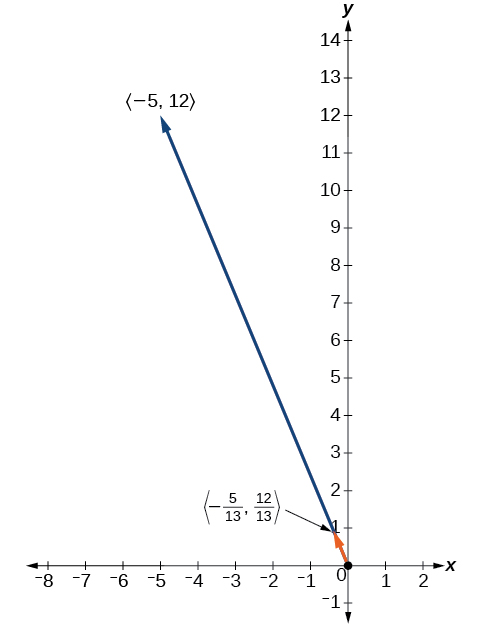
Figura\(\PageIndex{16}\)
Verifique se a magnitude do vetor unitário é igual\(1\). A magnitude de\(−\dfrac{5}{13}i+\dfrac{12}{13}j\) é dada como
\[\begin{align*} \sqrt{ {\left(−\dfrac{5}{13}\right)}^2+{ \left(\dfrac{12}{13}\right) }^2 } &= \sqrt{\dfrac{25}{169}+\dfrac{144}{169}} \\[4pt] &= \sqrt{\dfrac{169}{169}}\\ &=1 \end{align*}\]
O vetor\(u=\dfrac{5}{13}i+\dfrac{12}{13}j\) é o vetor unitário na mesma direção que\(v=⟨−5,12⟩\).
Executando operações com vetores em termos de\(i\) e\(j\)
Até agora, investigamos os fundamentos dos vetores: magnitude e direção, adição e subtração de vetores, multiplicação escalar, os componentes dos vetores e a representação de vetores geometricamente. Agora que estamos familiarizados com as estratégias gerais usadas no trabalho com vetores, representaremos vetores em coordenadas retangulares em termos de\(i\)\(j\) e.
Dado um vetor\(\vec{v}\) com ponto inicial\(P=(x_1,y_1)\) e ponto terminal\(Q=(x_2,y_2)\),\(\vec{v}\) é escrito como
\[v=(x_2−x_1)i+(y_1−y_2)j\]
O vetor de posição de\((0,0)\) para\((a,b)\), onde\((x_2−x_1)=a\) e\((y_2−y_1)=b\), é escrito como\(\vec{v} = \vec{ai}+ \vec{bj}\). Essa soma vetorial é chamada de combinação linear dos vetores\(\vec{i}\)\(\vec{j}\) e.
A magnitude de\(\vec{v} = \overrightarrow{ai} + \overrightarrow{bj}\) é dada como\(| v |=\sqrt{a^2+b^2}\). Veja a Figura\(\PageIndex{17}\).
.jpg)
Figura\(\PageIndex{17}\)
Dado um vetor\(\vec{v}\) com ponto inicial\(P=(2,−6)\) e ponto terminal\(Q=(−6,6)\), escreva o vetor em termos de\(\vec{i}\)\(\vec{j}\) e.
Solução
Comece escrevendo a forma geral do vetor. Em seguida, substitua as coordenadas pelos valores fornecidos.
\[\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] &=(−6−2)i+(6−(−6))j \\[4pt] &= −8i+12j \end{align*}\]
Dado o ponto inicial\(P_1=(−1,3)\) e o ponto terminal\(P_2=(2,7)\), escreva o vetor\(\vec{v}\) em termos de\(\vec{i}\)\(\vec{j}\) e.
Solução
Comece escrevendo a forma geral do vetor. Em seguida, substitua as coordenadas pelos valores fornecidos.
\[\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] v &= (2−(−1))i+(7−3)j \\[4pt] &= 3i+4j \end{align*}\]
Escreva o vetor\(\vec{u}\) com o ponto inicial\(P=(−1,6)\) e o ponto terminal\(Q=(7,−5)\) em termos de\(\vec{i}\)\(\vec{j}\) e.
- Responda
-
\(u=8i−11j\)
Executando operações em vetores em termos de\(i\) e\(j\)
Quando os vetores são escritos em termos de\(i\) e\(j\), podemos realizar adição, subtração e multiplicação escalar executando operações nos componentes correspondentes.
Dado\(v = ai + bj\) e\(u = ci + dj\), em seguida,
\[\begin{align*} v+u &= (a+c)i+(b+d)j \\[4pt] v−u &= (a−c)i+(b−d)j \end{align*}\]
Encontre a soma de\(v_1=2i−3j\)\(v_2=4i+5j\) e.
Solução
\[\begin{align*} v_1+v_2 &= (2+4)i+(−3+5)j \\[4pt] &= 6i+2j \end{align*}\]
Calculando a forma do componente de um vetor: direção
Vimos como desenhar vetores de acordo com seus pontos iniciais e terminais e como encontrar o vetor de posição. Também examinamos a notação de vetores desenhados especificamente no plano de coordenadas cartesianas usando\(i\)\(j\) e. Para qualquer um desses vetores, podemos calcular a magnitude. Agora, queremos combinar os pontos-chave e analisar mais detalhadamente as ideias de magnitude e direção.
O cálculo da direção segue o mesmo processo simples que usamos para coordenadas polares. Encontramos a direção do vetor encontrando o ângulo em relação à horizontal. Fazemos isso usando as identidades trigonométricas básicas, mas com a\(| v |\) substituição\(r\).
Dado um vetor de posição\(v=⟨x,y⟩\) e um ângulo de direção\(\theta\),
\[ \begin{align*} \cos \theta &= \dfrac{x}{|v|} \text{ and } \sin \theta=y|v| \\[4pt] x &= |v| \cos \theta \\[4pt] y &= |v| \sin \theta \end{align*}\]
Assim,\(v=xi+yj=| v | \cos \theta i+| v | \sin \theta j\), e a magnitude é expressa como\(| v |=\sqrt{x^2+y^2}\).
Escreva um vetor com comprimento\(7\) em um ângulo de em relação\(135°\) ao eixo x positivo em termos de magnitude e direção.
Solução
Usando as fórmulas de conversão\(x=| v | \cos \theta i\) e\(y=| v | \sin \theta j\), descobrimos que
\[ \begin{align*} x &= 7\cos(135°)i \\[4pt] &= −\dfrac{7\sqrt{2}}{2} \\[4pt] y &=7 \sin(135°)j \\[4pt] &= \dfrac{7\sqrt{2}}{2} \end{align*}\]
Esse vetor pode ser escrito\(v=7\cos(135°)i+7\sin(135°)j\) ou simplificado como
\(v=−\dfrac{7\sqrt{2}}{2}i+\dfrac{7\sqrt{2}}{2}j\)
Um vetor viaja da origem até o ponto\((3,5)\). Escreva o vetor em termos de magnitude e direção.
- Responda
-
\(v=\sqrt{34}\cos(59°)i+\sqrt{34}\sin(59°)j\)
Magnitude =\(34\)
\(\theta={\tan}^{−1}\left(\dfrac{5}{3}\right)=59.04°\)
Encontrando o produto escalar de dois vetores
Como discutimos anteriormente na seção, a multiplicação escalar envolve a multiplicação de um vetor por um escalar, e o resultado é um vetor. Como vimos, multiplicar um vetor por um número é chamado de multiplicação escalar. Se multiplicarmos um vetor por um vetor, há duas possibilidades: o produto escalar e o produto cruzado. Examinaremos apenas o produto escalar aqui; você pode encontrar o produto cruzado em cursos de matemática mais avançados.
O produto escalar de dois vetores envolve a multiplicação de dois vetores juntos, e o resultado é um escalar.
O produto escalar de dois vetores\(v=⟨a,b⟩\) e\(u=⟨c,d⟩\) é a soma do produto dos componentes horizontais e do produto dos componentes verticais.
\[v⋅u=ac+bd\]
Para encontrar o ângulo entre os dois vetores, use a fórmula abaixo.
\[\cos \theta=\dfrac{v}{| v |}⋅\dfrac{u}{| u |}\]
Encontre o produto escalar de\(v=⟨5,12⟩\)\(u=⟨−3,4⟩\) e.
Solução
Usando a fórmula, temos
\[\begin{align*} v⋅u &= ⟨5,12⟩⋅⟨−3,4⟩ \\[4pt] &= 5⋅(−3)+12⋅4 \\[4pt] &= −15+48 \\[4pt] &= 33 \end{align*}\]
Encontre o produto escalar de\(v_1 = 5i + 2j\)\(v_2 = 3i + 7j\) e. Em seguida, encontre o ângulo entre os dois vetores.
Solução
Encontrando o produto escalar, multiplicamos os componentes correspondentes.
\[ \begin{align*} v_1⋅v_2 &= ⟨5,2⟩⋅⟨3,7⟩ \\[4pt] &= 5⋅3+2⋅7 \\[4pt] &= 15+14 \\[4pt] &= 29 \end{align*}\]
Para encontrar o ângulo entre eles, usamos a fórmula\(\cos \theta=\dfrac{v}{|v|}⋅\dfrac{u}{|u|}\).
\[\begin{align*} \dfrac{v}{|v|}\cdot \dfrac{u}{|u|} &= \left \langle \dfrac{5}{\sqrt{29}}+\dfrac{2}{\sqrt{29}} \right \rangle \cdot \left \langle \dfrac{3}{\sqrt{58}}+\dfrac{7}{\sqrt{58}} \right \rangle \\[4pt] &=\dfrac{5}{\sqrt{29}}\cdot \dfrac{3}{\sqrt{58}}+\dfrac{2}{\sqrt{29}}\cdot \dfrac{7}{\sqrt{58}} \\[4pt] &= \dfrac{15}{\sqrt{1682}}+\dfrac{14}{\sqrt{1682}}\\ &=\dfrac{29}{\sqrt{1682}} \\[4pt] &= 0.707107 \\[4pt] {\cos}^{-1}(0.707107) &= 45° \end{align*}\]
Veja a Figura\(\PageIndex{18}\).
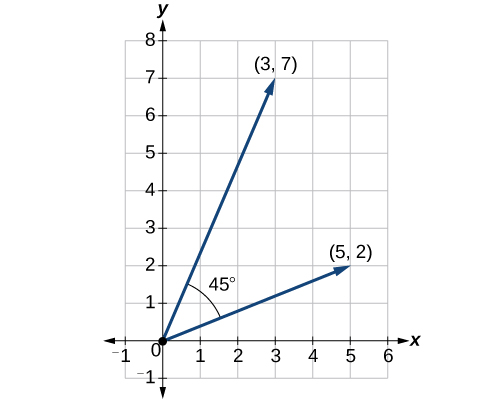
Figura\(\PageIndex{18}\)
Encontre o ângulo entre\(u=⟨−3,4⟩\)\(v=⟨5,12⟩\) e.
Solução
Usando a fórmula, temos
\[\begin{align*} \theta &= {\cos}^{−1}\left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) \\[4pt] \left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) &= \dfrac{−3i+4j}{5}⋅\dfrac{5i+12j}{13} \\[4pt] &= \left(− \dfrac{3}{5}⋅ \dfrac{5}{13}\right)+\left(\dfrac{4}{5}⋅ \dfrac{12}{13}\right) \\[4pt] &= −\dfrac{15}{65}+\dfrac{48}{65} \\[4pt] &= \dfrac{33}{65} \\[4pt] \theta &= {\cos}^{−1}\left(\dfrac{33}{65}\right) \\[4pt] &= 59.5^{\circ} \end{align*}\]
Veja a Figura\(\PageIndex{19}\).
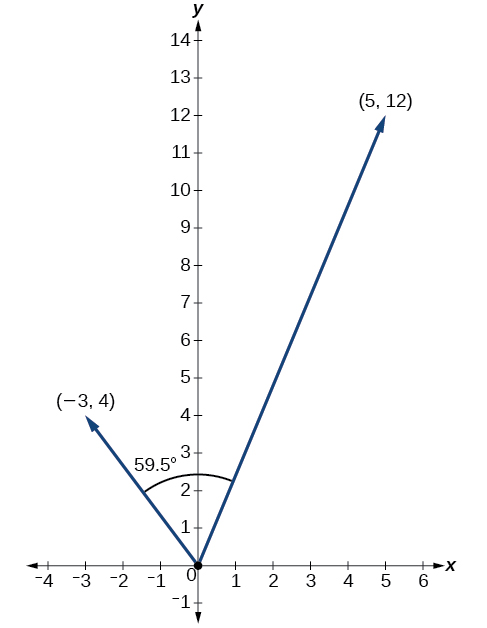
Figura\(\PageIndex{19}\)
Agora temos as ferramentas para resolver o problema que apresentamos na abertura da seção.
Um avião está voando a uma velocidade aérea de\(200\) milhas por hora em direção a um rumo SE de\(140°\). Um vento norte (de norte a sul) está soprando a\(16.2\) milhas por hora. Quais são a velocidade do solo e o rumo real do avião? Veja a Figura\(\PageIndex{20}\).
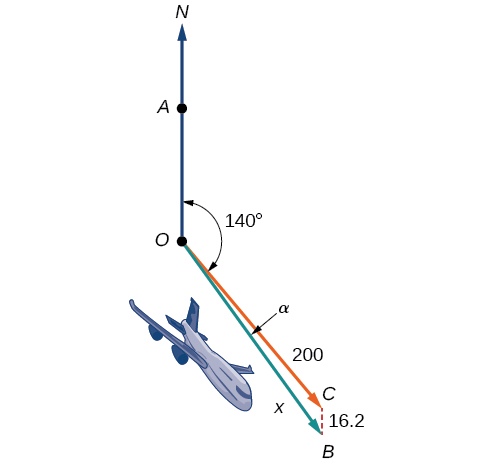
Figura\(\PageIndex{20}\)
Solução
A velocidade do solo é representada\(x\) no diagrama, e precisamos encontrar o ângulo\(\alpha\) para calcular o rolamento ajustado, que será\(140°+\alpha\).
Observe na Figura\(\PageIndex{20}\) que esse ângulo\(\angle BCO\) deve ser igual ao ângulo\(\angle AOC\) pela regra de ângulos internos alternados, então o ângulo\(\angle BCO\) é 140°. Podemos encontrar\(x\) pela Lei dos Cossenos:
\[\begin{align*} x^2 &= {(16.2)}^2+{(200)}^2−2(16.2)(200) \cos(140°) \\[4pt] x^2 &= 45,226.41 \\[4pt] x &= \sqrt{45,226.41} \\[4pt] x &= 212.7 \end{align*}\]
A velocidade do solo é de aproximadamente\(213\) milhas por hora. Agora podemos calcular o rumo usando a Lei de Sines.
\[\begin{align*} \dfrac{\sin \alpha}{16.2} &= \dfrac{\sin(140°)}{212.7} \\[4pt] \sin \alpha &= \dfrac{16.2 \sin(140°)}{212.7} \\[4pt] &=0.04896 \\[4pt] {\sin}^{−1}(0.04896) &= 2.8° \end{align*}\]
Portanto, o avião tem um rolamento SE de\(140°+2.8°=142.8°\). A velocidade do solo é de\(212.7\) milhas por hora.
Conceitos-chave
- O vetor de posição tem seu ponto inicial na origem. Veja o exemplo\(\PageIndex{1}\).
- Se o vetor de posição for o mesmo para dois vetores, eles serão iguais. Veja o exemplo\(\PageIndex{2}\).
- Os vetores são definidos por sua magnitude e direção. Veja o exemplo\(\PageIndex{3}\).
- Se dois vetores tiverem a mesma magnitude e direção, eles serão iguais. Veja o exemplo\(\PageIndex{4}\).
- A adição e a subtração de vetores resultam em um novo vetor encontrado pela adição ou subtração dos elementos correspondentes. Veja o exemplo\(\PageIndex{5}\).
- A multiplicação escalar é multiplicar um vetor por uma constante. Somente a magnitude muda; a direção permanece a mesma. Veja o exemplo\(\PageIndex{6}\) e o exemplo\(\PageIndex{7}\).
- Os vetores são compostos por dois componentes: o componente horizontal ao longo do\(x\) eixo positivo e o componente vertical ao longo do\(y\) eixo positivo. Veja o exemplo\(\PageIndex{8}\).
- O vetor unitário na mesma direção de qualquer vetor diferente de zero é encontrado dividindo o vetor por sua magnitude.
- A magnitude de um vetor no sistema de coordenadas retangulares é\(| v |=\sqrt{a^2+b^2}\). Veja o exemplo\(\PageIndex{9}\).
- No sistema de coordenadas retangulares, os vetores unitários podem ser representados em termos de\(ii\) e\(jj\) onde\(i\) representa o componente horizontal e\(j\) representa o componente vertical. Então,\(v = ai + bj\) é um múltiplo escalar de\(v\) por números reais\(a\)\(b\) e. Veja o exemplo\(\PageIndex{10}\) e o exemplo\(\PageIndex{11}\).
- Adicionar e subtrair vetores em termos de\(i\) e\(j\) consiste em somar ou subtrair coeficientes correspondentes\(i\) e coeficientes correspondentes de\(j\). Veja o exemplo\(\PageIndex{12}\).
- Um vetor\(v = ai + bj\) é escrito em termos de magnitude e direção como\(v=| v |\cos \theta i+| v |\sin \theta j\). Veja o exemplo\(\PageIndex{13}\).
- O produto escalar de dois vetores é o produto dos\(i\) termos mais o produto dos\(j\) termos. Veja o exemplo\(\PageIndex{14}\).
- Podemos usar o produto escalar para encontrar o ângulo entre dois vetores. Exemplo\(\PageIndex{15}\) e exemplo\(\PageIndex{16}\).
- Os produtos Dot são úteis para muitos tipos de aplicações físicas. Veja o exemplo\(\PageIndex{17}\).


