8.5: Forma polar de números complexos
- Page ID
- 189146
- Faça um gráfico de números complexos no plano complexo.
- Encontre o valor absoluto de um número complexo.
- Escreva números complexos na forma polar.
- Converta um número complexo da forma polar para a retangular.
- Encontre produtos de números complexos na forma polar.
- Encontre quocientes de números complexos na forma polar.
- Encontre potências de números complexos na forma polar.
- Encontre raízes de números complexos na forma polar.
“Deus fez os números inteiros; tudo o mais é obra do homem.” Essa citação bastante famosa do matemático alemão do século XIX Leopold Kronecker prepara o terreno para esta seção sobre a forma polar de um número complexo. Os números complexos foram inventados por pessoas e representam mais de mil anos de investigação e luta contínuas de matemáticos como Pitágoras, Descartes, De Moivre, Euler, Gauss e outros. Números complexos responderam a perguntas que, durante séculos, confundiram as maiores mentes da ciência.
Encontramos números complexos pela primeira vez na seção sobre Números Complexos. Nesta seção, vamos nos concentrar na mecânica do trabalho com números complexos: tradução de números complexos da forma polar para a forma retangular e vice-versa, interpretação de números complexos no esquema de aplicações e aplicação do Teorema de De Moivre.
Traçando números complexos no plano complexo
Traçar um número complexo\(a+bi\) é semelhante a traçar um número real, exceto que o eixo horizontal representa a parte real do número\(a\), e o eixo vertical representa a parte imaginária do número,\(bi\).
- Identifique o eixo horizontal como o eixo real e o eixo vertical como o eixo imaginário.
- Faça um gráfico do ponto no plano complexo movendo\(a\) as unidades na direção horizontal e\(b\) as unidades na direção vertical.
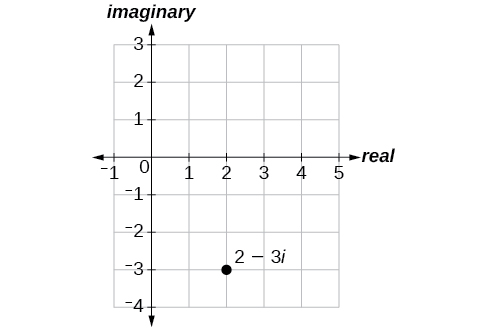
Faça um gráfico do número complexo\(2−3i\) no plano complexo.
Solução
Da origem, mova duas unidades na direção horizontal positiva e três unidades na direção vertical negativa. Veja a Figura\(\PageIndex{1}\).
Faça um gráfico do ponto\(1+5i\) no plano complexo.
- Responda
-
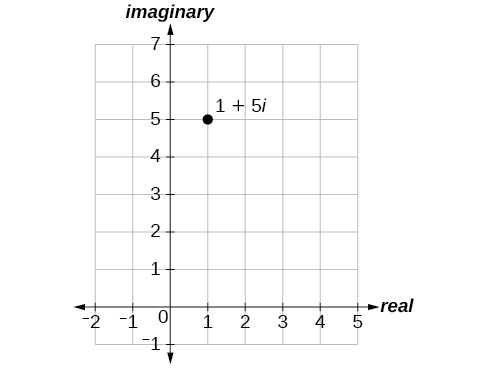
Figura\(\PageIndex{2}\)
Encontrando o valor absoluto de um número complexo
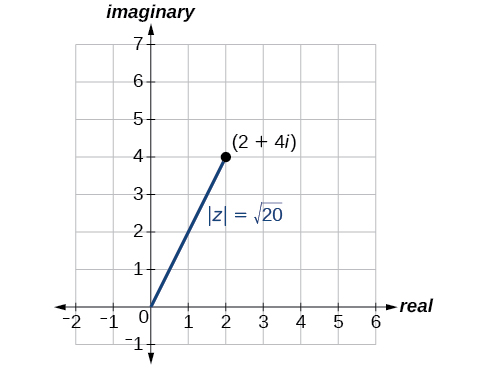
O primeiro passo para trabalhar com um número complexo na forma polar é encontrar o valor absoluto. O valor absoluto de um número complexo é o mesmo que sua magnitude, ou\(| z |\). Ele mede a distância da origem até um ponto no plano. Por exemplo, o gráfico de\(z=2+4i\), na Figura\(\PageIndex{3}\), mostra\(| z |\).
Dado\(z=x+yi\), um número complexo, o valor absoluto de\(z\) é definido como
\[| z |=\sqrt{x^2+y^2}\]
É a distância da origem até o ponto\((x,y)\).
Observe que o valor absoluto de um número real fornece a distância do número de\(0\), enquanto o valor absoluto de um número complexo fornece a distância do número da origem,\((0, 0)\).
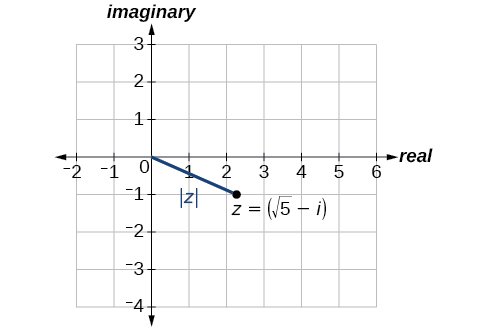
Encontre o valor absoluto de\(z=\sqrt{5}−i\).
Solução
Usando a fórmula, temos
\[\begin{align*} |z| &= \sqrt{x^2+y^2} \\ |z| &= \sqrt{{(\sqrt{5})}^2+{(-1)}^2} \\ |z| &= \sqrt{5+1} \\ |z| &= \sqrt{6} \end{align*}\]
Veja a Figura\(\PageIndex{4}\).
Encontre o valor absoluto do número complexo\(z=12−5i\).
- Responda
-
\(13\)
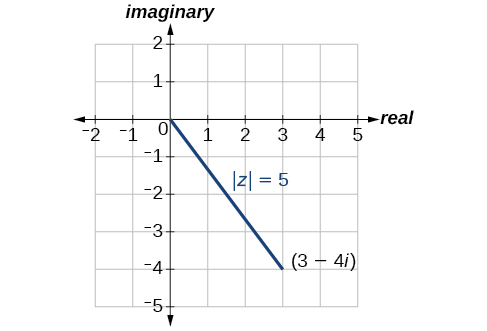
Dado\(z=3−4i\), encontre\(| z |\).
Solução
Usando a fórmula, temos
\[\begin{align*} | z | &= \sqrt{x^2+y^2} \\ | z | &= \sqrt{{(3)}^2+{(-4)}^2} \\ | z | &= \sqrt{9+16} \\ | z | &= \sqrt{25} \\ | z | &= 5 \end{align*}\]
O valor absoluto\(z\) é\(5\). Veja a Figura\(\PageIndex{5}\).
Dado\(z=1−7i\), encontre\(| z |\).
- Responda
-
\(| z |=\sqrt{50}=5\sqrt{2}\)
Escrevendo números complexos na forma polar
A forma polar de um número complexo expressa um número em termos de um ângulo\(\theta\) e sua distância da origem\(r\). Dado um número complexo na forma retangular expresso como\(z=x+yi\), usamos as mesmas fórmulas de conversão que usamos para escrever o número na forma trigonométrica:
\[\begin{align*} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align*}\]
Analisamos essas relações na Figura\(\PageIndex{6}\).
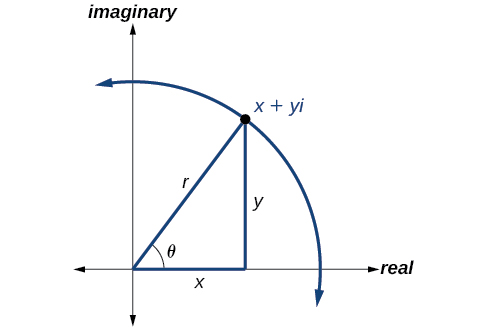
Usamos o termo módulo para representar o valor absoluto de um número complexo ou a distância da origem até o ponto\((x,y)\). O módulo, então, é o mesmo que\(r\) o raio na forma polar. Usamos\(\theta\) para indicar o ângulo de direção (assim como nas coordenadas polares). Substituindo, temos
\[\begin{align*} z &= x+yi \\ z &= r \cos \theta+(r \sin \theta)i \\ z &= r(\cos \theta+i \sin \theta) \end{align*}\]
Escrever um número complexo na forma polar envolve as seguintes fórmulas de conversão:
\[\begin{align} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align}\]
Fazendo uma substituição direta, temos
\[\begin{align} z &= x+yi \\ z &= (r \cos \theta)+i(r \sin \theta) \\ z &= r(\cos \theta+i \sin \theta) \end{align}\]
onde\(r\) está o módulo e\(\theta\) é o argumento. Costumamos usar a abreviatura\(r\; cis \theta\) para representar\(r(\cos \theta+i \sin \theta)\).
Expresse o número complexo\(4i\) usando coordenadas polares.
Solução
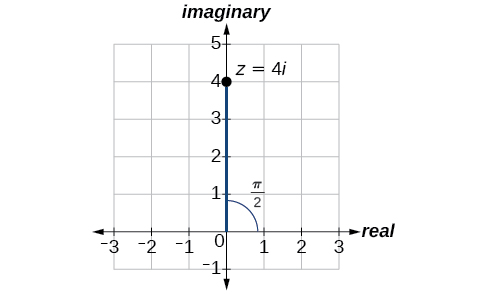
No plano complexo, o número\(z=4i\) é o mesmo de\(z=0+4i\). Escrevendo-o na forma polar, temos que calcular\(r\) primeiro.
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{0^2+4^2} \\ r &= \sqrt{16} \\ r &= 4 \end{align*}\]
Em seguida, examinamos\(x\). Se\(x=r \cos \theta\), e\(x=0\), então\(\theta=\dfrac{\pi}{2}\). Nas coordenadas polares, o número complexo\(z=0+4i\) pode ser escrito como\(z=4\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right) \text{ or } 4\; cis\left( \dfrac{\pi}{2}\right)\). Veja a Figura\(\PageIndex{7}\).
\(z=3i\)Expresse como\(r\space cis \theta\) na forma polar.
- Responda
-
\(z=3\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right)\)
Encontre a forma polar de\(−4+4i\).
Solução
Primeiro, encontre o valor de\(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(−4)}^2+(4^2)} \\ r &= \sqrt{32} \\ r &= 4\sqrt{2} \end{align*}\]
Encontre o ângulo\(\theta\) usando a fórmula:
\[\begin{align*} \cos \theta &= \dfrac{x}{r} \\ \cos \theta &= \dfrac{−4}{4\sqrt{2}} \\ \cos \theta &= −\dfrac{1}{\sqrt{2}} \\ \theta &= {\cos}^{−1} \left(−\dfrac{1}{\sqrt{2}}\right)\\ &= \dfrac{3\pi}{4} \end{align*}\]
Portanto, a solução é\(4\sqrt{2}\space cis \left(\dfrac{3\pi}{4}\right)\).
Escreva\(z=\sqrt{3}+i\) na forma polar.
- Responda
-
\(z=2\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Convertendo um número complexo da forma polar para retangular
Converter um número complexo da forma polar para a forma retangular é uma questão de avaliar o que é dado e usar a propriedade distributiva. Em outras palavras, dado\(z=r(\cos \theta+i \sin \theta)\), primeiro avalie as funções trigonométricas\(\cos \theta\)\(\sin \theta\) e. Em seguida, multiplique por\(r\).
Converta a forma polar de um determinado número complexo em forma retangular:
\(z=12\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Solução
Começamos avaliando as expressões trigonométricas.
\[\begin{align*} \cos\left(\dfrac{\pi}{6}\right)&= \dfrac{\sqrt{3}}{2} \text{ and } \sin(\dfrac{\pi}{6})=\dfrac{1}{2}\\ \text {After substitution, the complex number is}\\ z&= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \end{align*}\]
Nós aplicamos a propriedade distributiva:
\[\begin{align*} z &= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\ &= (12)\dfrac{\sqrt{3}}{2}+(12)\dfrac{1}{2}i \\ &= 6\sqrt{3}+6i \end{align*}\]
A forma retangular do ponto dado na forma complexa é\(6\sqrt{3}+6i\).
Encontre a forma retangular do número complexo dado\(r=13\)\(\tan \theta=\dfrac{5}{12}\) e.
Solução
Se\(\tan \theta=\dfrac{5}{12}\), e\(\tan \theta=\dfrac{y}{x}\), determinamos primeiro\(r=\sqrt{x^2+y^2}=\sqrt{122+52}=13\). Em seguida, encontramos\(\cos \theta=\dfrac{x}{r}\)\(\sin \theta=\dfrac{y}{r}\) e.
\[\begin{align*} z &= 13\left(\cos \theta+i \sin \theta\right) \\ &= 13\left(\dfrac{12}{13}+\dfrac{5}{13}i\right) \\ &=12+5i \end{align*}\]
A forma retangular de um determinado número na forma complexa é\(12+5i\).
Converta o número complexo em forma retangular:
\(z=4\left(\cos \dfrac{11\pi}{6}+i \sin \dfrac{11\pi}{6}\right)\)
- Responda
-
\(z=2\sqrt{3}−2i\)
Encontrando produtos de números complexos na forma polar
Agora que podemos converter números complexos em forma polar, aprenderemos como realizar operações em números complexos na forma polar. No restante desta seção, trabalharemos com fórmulas desenvolvidas pelo matemático francês Abraham de Moivre (1667-1754). Essas fórmulas tornaram o trabalho com produtos, quocientes, potências e raízes de números complexos muito mais simples do que parecem. As regras são baseadas na multiplicação dos módulos e na adição dos argumentos.
Se\(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) e\(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), então o produto desses números é dado como:
\[\begin{align} z_1z_2 &= r_1r_2[ \cos(\theta_1+\theta_2)+i \sin(\theta_1+\theta_2) ] \\ z_1z_2 &= r_1r_2\space cis(\theta_1+\theta_2) \end{align}\]
Observe que o produto exige a multiplicação dos módulos e a adição dos ângulos.
Encontre o produto de\(z_1z_2\), dado\(z_1=4(\cos(80°)+i \sin(80°))\)\(z_2=2(\cos(145°)+i \sin(145°))\) e.
Solução
Siga a fórmula
\[\begin{align*} z_1z_2 &= 4⋅2[\cos(80°+145°)+i \sin(80°+145°)] \\ z_1z_2 &= 8[\cos(225°)+i \sin(225°)] \\ z_1z_2 &= 8\left[\cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ z_1z_2 &= 8\left[−\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ z_1z_2 &= −4\sqrt{2}−4i\sqrt{2} \end{align*}\]
Encontrando quocientes de números complexos na forma polar
O quociente de dois números complexos na forma polar é o quociente dos dois módulos e a diferença dos dois argumentos.
Se\(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) e\(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), então o quociente desses números é
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}[\cos(\theta_1−\theta_2)+i \sin(\theta_1−\theta_2) ],\space z_2≠0\]
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}\space cis(\theta_1−\theta_2),\space z_2≠0\]
Observe que os módulos são divididos e os ângulos são subtraídos.
- Divida\(\dfrac{r_1}{r_2}\).
- Encontre\(\theta_1−\theta_2\).
- Substitua os resultados na fórmula:\(z=r(\cos \theta+i \sin \theta)\). \(r\)Substitua\(\dfrac{r_1}{r_2}\) por e\(\theta\) substitua por\(\theta_1−\theta_2\).
- Calcule as novas expressões trigonométricas e multiplique por\(r\).
Encontre o quociente de\(z_1=2(\cos(213°)+i \sin(213°))\)\(z_2=4(\cos(33°)+i \sin(33°))\) e.
Solução
Usando a fórmula, temos
\[\begin{align*} \dfrac{z_1}{z_2} &= \dfrac{2}{4}[\cos(213°−33°)+i \sin(213°−33°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[\cos(180°)+i \sin(180°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[−1+0i] \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2}+0i \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2} \end{align*}\]
Encontre o produto e o quociente de\(z_1=2\sqrt{3}(\cos(150°)+i \sin(150°))\)\(z_2=2(\cos(30°)+i \sin(30°))\) e.
- Responda
-
\(z_1z_2=−4\sqrt{3}\);\(\dfrac{z_1}{z_2}=−\dfrac{\sqrt{3}}{2}+\dfrac{3}{2}i\)
Encontrando poderes de números complexos na forma polar
Encontrar poderes de números complexos é bastante simplificado usando o Teorema de De Moivre. Ele afirma que, para um número inteiro positivo\(n\),\(z^n\) é encontrado elevando o módulo à\(n^{th}\) potência e multiplicando o argumento por\(n\). É o método padrão usado na matemática moderna.
Se\(z=r(\cos \theta+i \sin \theta)\) for um número complexo, então
\[\begin{align} z^n &= r^n[\cos(n\theta)+i \sin(n\theta) ] \\ z^n &= r^n\space cis(n\theta) \end{align}\]
onde\(n\) é um número inteiro positivo.
Avalie a expressão\({(1+i)}^5\) usando o Teorema de De Moivre.
Solução
Como o Teorema de Moivre se aplica a números complexos escritos na forma polar, devemos primeiro escrever\((1+i)\) na forma polar. Vamos encontrar\(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(1)}^2+{(1)}^2} \\ r &= \sqrt{2} \end{align*}\]
Então encontramos\(\theta\). Usar a fórmula\(\tan \theta=\dfrac{y}{x}\) dá
\[\begin{align*} \tan \theta &= \dfrac{1}{1} \\ \tan \theta &= 1 \\ \theta &= \dfrac{\pi}{4} \end{align*}\]
Use o Teorema de De Moivre para avaliar a expressão.
\[\begin{align*} {(a+bi)}^n &= r^n[\cos(n\theta)+i \sin(n\theta)] \\ {(1+i)}^5 &= {(\sqrt{2})}^5\left[ \cos\left(5⋅\dfrac{\pi}{4}\right)+i \sin\left(5⋅\dfrac{\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ \cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ −\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ {(1+i)}^5 &= −4−4i \end{align*}\]
Encontrando raízes de números complexos na forma polar
Para encontrar a\(n^{th}\) raiz de um número complexo na forma polar, usamos o Teorema da\(n^{th}\) Raiz ou o Teorema de De Moivre e elevamos o número complexo a uma potência com um expoente racional. Existem várias maneiras de representar uma fórmula para encontrar\(n^{th}\) raízes de números complexos na forma polar.
Para encontrar a\(n^{th}\) raiz de um número complexo na forma polar, use a fórmula dada como
\[z^{\tfrac{1}{n}}=r^{\tfrac{1}{n}}\left[ \cos\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right)+i \sin\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right) \right]\]
onde\(k=0, 1, 2, 3, . . . , n−1\). Nós\(\dfrac{2k\pi}{n}\) adicionamos para obter as raízes periódicas.\(\dfrac{\theta}{n}\)
Avalie as raízes cúbicas de\(z=8\left(\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\right)\).
Solução
Nós temos
\[\begin{align*} z^{\frac{1}{3}} &= 8^{\frac{1}{3}}\left[ \cos\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right) \right] \\ z^{\frac{1}{3}} &= 2\left[ \cos\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right) \right] \end{align*}\]
Haverá três raízes:\(k=0, 1, 2\). Quando\(k=0\), temos
\(z^{\frac{1}{3}}=2\left(\cos\left(\dfrac{2\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}\right)\right)\)
Quando\(k=1\), temos
\[\begin{align*} z^{\frac{1}{3}} &=2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right) \right] \;\;\;\;\;\;\;\;\; \text{Add }\dfrac{2(1)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{8\pi}{9}\right)+i \sin\left(\dfrac{8\pi}{9}\right)\right) \end{align*}\]
Quando\(k=2\), temos
\[\begin{align*} z^{\frac{1}{3}} &= 2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right) \right] \;\;\;\;\;\;\; \text{Add }\dfrac{2(2)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{14\pi}{9}\right)+i \sin\left(\dfrac{14\pi}{9}\right)\right) \end{align*}\]
Lembre-se de encontrar o denominador comum para simplificar frações em situações como essa. Pois\(k=1\), a simplificação do ângulo é
\[\begin{align*} \dfrac{\dfrac{2\pi}{3}}{3}+\dfrac{2(1)\pi}{3} &= \dfrac{2\pi}{3}(\dfrac{1}{3})+\dfrac{2(1)\pi}{3}\left(\dfrac{3}{3}\right) \\ &=\dfrac{2\pi}{9}+\dfrac{6\pi}{9} \\ &=\dfrac{8\pi}{9} \end{align*}\]
Encontre as quatro quartas raízes do\(16(\cos(120°)+i \sin(120°))\).
- Responda
-
\(z_0=2(\cos(30°)+i \sin(30°))\)
\(z_1=2(\cos(120°)+i \sin(120°))\)
\(z_2=2(\cos(210°)+i \sin(210°))\)
\(z_3=2(\cos(300°)+i \sin(300°))\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com formas polares de números complexos.
- O produto e o quociente de números complexos na forma trigonométrica
- Teorema de De Moivre
Conceitos-chave
- Os números complexos no formulário\(a+bi\) são plotados no plano complexo, semelhante à forma como as coordenadas retangulares são plotadas no plano retangular. Identifique o\(x\) eixo -como o eixo real e o eixo\(y\) - como o eixo imaginário. Veja o exemplo\(\PageIndex{1}\).
- O valor absoluto de um número complexo é o mesmo que sua magnitude. É a distância da origem até o ponto:\(| z |=\sqrt{a^2+b^2}\). Veja o exemplo\(\PageIndex{2}\) e o exemplo\(\PageIndex{3}\).
- Para escrever números complexos na forma polar, usamos as fórmulas\(x=r \cos \theta\)\(y=r \sin \theta\),\(r=\sqrt{x^2+y^2}\) e. Então,\(z=r(\cos \theta+i \sin \theta)\). Veja o exemplo\(\PageIndex{4}\) e o exemplo\(\PageIndex{5}\).
- Para converter da forma polar para a forma retangular, primeiro avalie as funções trigonométricas. Em seguida, multiplique por\(r\). Veja o exemplo\(\PageIndex{6}\) e o exemplo\(\PageIndex{7}\).
- Para encontrar o produto de dois números complexos, multiplique os dois módulos e adicione os dois ângulos. Avalie as funções trigonométricas e multiplique usando a propriedade distributiva. Veja o exemplo\(\PageIndex{8}\).
- Para encontrar o quociente de dois números complexos na forma polar, encontre o quociente dos dois módulos e a diferença dos dois ângulos. Veja o exemplo\(\PageIndex{9}\).
- Para encontrar a potência de um número complexo\(z^n\), aumente\(r\) até a potência\(n\) e multiplique\(\theta\) por\(n\). Veja o exemplo\(\PageIndex{10}\).
- Encontrar as raízes de um número complexo é o mesmo que elevar um número complexo a uma potência, mas usar um expoente racional. Veja o exemplo\(\PageIndex{11}\).


