8.4: Coordenadas polares - Gráficos

Last updated
Save as PDF

Page ID: 189154

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Teste a simetria das equações polares.
Representar graficamente equações polares traçando pontos.

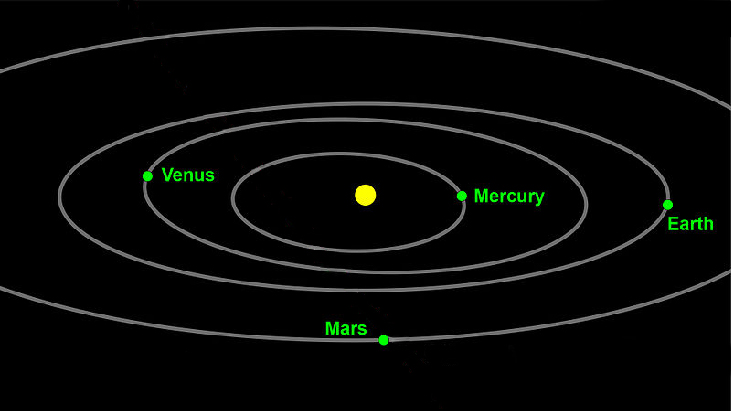
A Primeira Lei do Movimento Planetário de Keplar argumenta que os planetas se movem pelo espaço em órbitas elípticas e periódicas em torno do sol, conforme mostrado na Figura$\PageIndex{1}$. Eles estão em constante movimento, então fixar uma posição exata de qualquer planeta é válido apenas por um momento. Em outras palavras, só podemos fixar a posição instantânea de um planeta. Esta é uma aplicação de coordenadas polares, representada como$(r,\theta)$. Nós interpretamos$r$ como a distância do sol e$\theta$ como o rumo angular do planeta, ou sua direção a partir de um ponto fixo no sol. Nesta seção, vamos nos concentrar no sistema polar e nos gráficos que são gerados diretamente das coordenadas polares.

Ilustração do sistema solar com o sol no centro e as órbitas dos planetas Mercúrio, Vênus, Terra e Marte mostrada. — Figura$\PageIndex{1}$: Os planetas seguem caminhos elípticos enquanto orbitam ao redor do Sol. (crédito: modificação do trabalho da NASA/JPL-Caltech)

Testando equações polares para simetria

Assim como uma equação retangular, como$y=x^2$ descreve a relação entre$x$ e$y$ em uma grade cartesiana, uma equação polar descreve uma relação entre$r$ e$\theta$ em uma grade polar. Lembre-se de que o par de coordenadas$(r,\theta)$ indica que nos movemos no sentido anti-horário a partir do eixo polar ($x$eixo positivo) por um ângulo de$\theta$ e estendemos um raio das$r$ unidades do polo (origem) na direção de$\theta$. Todos os pontos que satisfazem a equação polar estão no gráfico.

A simetria é uma propriedade que nos ajuda a reconhecer e traçar o gráfico de qualquer equação. Se uma equação tem um gráfico simétrico em relação a um eixo, isso significa que se dobrássemos o gráfico ao meio sobre esse eixo, a parte do gráfico de um lado coincidiria com a parte do outro lado. Ao realizar três testes, veremos como aplicar as propriedades da simetria às equações polares. Além disso, usaremos simetria (além de traçar pontos-chave, zeros e máximos de$r$) para determinar o gráfico de uma equação polar.

No primeiro teste, consideramos a simetria em relação à linha$\theta=\dfrac{\pi}{2}$ ($y$eixo -). $(r,\theta)$Substituímos por$(−r,−\theta)$ para determinar se a nova equação é equivalente à equação original. Por exemplo, suponha que recebamos a equação$r=2 \sin \theta$;

\[\begin{align*} r&= 2 \sin \theta \\ -r&= 2 \sin -\theta \qquad \text{Replace } (r,\theta) \text{ with }(-r,-\theta). \\ -r&= -2 \sin \theta \qquad \text{Identity: }\sin(-\theta)=-\sin \theta. \\ r&= 2 \sin \theta \qquad \text{Multiply both sides by }-1 \end{align*}\]

Essa equação exibe simetria em relação à linha$\theta=\dfrac{\pi}{2}$.

No segundo teste, consideramos a simetria em relação ao eixo polar ($x$eixo -). $(r,\theta)$Substituímos por$(r,−\theta)$ ou$(−r,\pi−\theta)$ para determinar a equivalência entre a equação testada e a original. Por exemplo, suponha que recebamos a equação$r=1−2 \cos \theta$.

\[\begin{align*} r&= 1-2 \cos \theta \\ r&= 1-2 \cos(-\theta)\qquad \text{Replace }(r,\theta) \text{ with }(r,-\theta). \\ r&= 1-2 \cos \theta \qquad \text{Even/Odd identity} \end{align*}\]

O gráfico dessa equação exibe simetria em relação ao eixo polar.

No terceiro teste, consideramos a simetria em relação ao polo (origem). $(r,\theta)$Substituímos por$(−r,\theta)$ para determinar se a equação testada é equivalente à equação original. Por exemplo, suponha que recebamos a equação$r=2 \sin(3\theta)$.

$r=2 \sin(3\theta)$

$−r=2 \sin(3\theta)$

A equação falhou no teste de simetria, mas isso não significa que ela não seja simétrica em relação ao polo. A aprovação em um ou mais dos testes de simetria verifica se a simetria será exibida em um gráfico. No entanto, falhar nos testes de simetria não indica necessariamente que um gráfico não será simétrico em relação à linha$\theta=\dfrac{\pi}{2}$, ao eixo polar ou ao polo. Nesses casos, podemos confirmar que a simetria existe traçando pontos refletores no eixo aparente de simetria ou no polo. O teste de simetria é uma técnica que simplifica a representação gráfica das equações polares, mas sua aplicação não é perfeita.

Nota: TESTES DE SIMETRIA

Uma equação polar descreve uma curva na grade polar. O gráfico de uma equação polar pode ser avaliado para três tipos de simetria, conforme mostrado na Figura$\PageIndex{2}$.

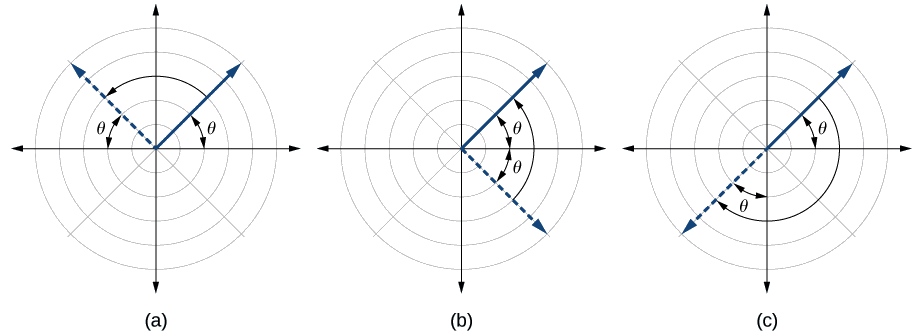
3 gráficos lado a lado. (A) mostra um raio que se estende até Q 1 e sua versão simétrica em Q 2. (B) mostra um raio que se estende até Q 1 e sua versão simétrica em Q 4. (C) mostra um raio que se estende até Q 1 e sua versão simétrica em Q 3. Consulte a legenda para obter mais informações. — Figura$\PageIndex{2}$: (a) Um gráfico é simétrico em relação à linha$\theta=\dfrac{\pi}{2}$ (eixo y) se a substituição por$(r,\theta)$$(−r,−\theta)$ produzir uma equação equivalente. (b) Um gráfico é simétrico em relação ao eixo polar (eixo x) se for$(r,\theta)$ substituído por$(r,−\theta)$ ou$(−r,\pi−\theta)$ produzir uma equação equivalente. (c) Um gráfico é simétrico em relação ao pólo (origem) se$(r,\theta)$ a substituição por$(−r,\theta)$ produzir uma equação equivalente.

Como fazer: Dada uma equação polar, teste a simetria.

Substitua a combinação apropriada de componentes por$(r,\theta)$:$(−r,−\theta)$ por$\theta=\dfrac{\pi}{2}$ simetria;$(r,−\theta)$ por simetria do eixo polar; e$(−r,\theta)$ por simetria em relação ao polo.
Se as equações resultantes forem equivalentes em um ou mais dos testes, o gráfico produzirá a simetria esperada.

Exemplo$\PageIndex{1}$: Testing a Polar Equation for Symmetry

Teste a equação quanto$r=2 \sin \theta$ à simetria.

Solução

Teste cada um dos três tipos de simetria.

1)$(r,\theta)$ Substituir por$(−r,−\theta)$ produz o mesmo resultado. Assim, o gráfico é simétrico em relação à linha$\theta=\dfrac{\pi}{2}$.

$−r=2 \sin(−\theta)$

$−r=−2 \sin \theta$Identidade ainda estranha

$r=2 \sin \theta$Multiplique por$−1$

Aprovado

2)$\theta$ Substituir por$−\theta$ não produz a mesma equação. Portanto, o gráfico falha no teste e pode ou não ser simétrico em relação ao eixo polar.

$r=2 \sin(−\theta)$

$r=−2 \sin \theta$Identidade ainda estranha

$r=−2 \sin \theta ≠ 2 \sin \theta$

Falhou

3)$r$ Substituir por$–r$ altera a equação e falha no teste. O gráfico pode ou não ser simétrico em relação ao polo.

$−r=2 \sin \theta$

$r=−2 \sin \theta ≠2 \sin \theta$

Falhou

Análise

Usando uma calculadora gráfica, podemos ver que a equação$r=2 \sin \theta$ é uma circunferência$(0,1)$ centrada no raio$r=1$ e é de fato simétrica à linha$\theta=\dfrac{\pi}{2}$. Também podemos ver que o gráfico não é simétrico com o eixo polar ou com o polo. Veja a Figura$\PageIndex{3}$.

Gráfico do círculo dado na grade de coordenadas polares. O centro está em (0,1) e tem raio 1. — Figura$\PageIndex{3}$

Exercício$\PageIndex{1}$

Teste a equação para simetria:$r=−2 \cos \theta$.

Resposta: A equação falha no teste de simetria em relação à linha$\theta=\dfrac{\pi}{2}$ e em relação ao polo. Ele passa no teste de simetria do eixo polar.

Representação gráfica de equações polares traçando pontos

Para representar graficamente no sistema de coordenadas retangulares, construímos uma tabela de$y$ valores$x$ e. Para representar graficamente no sistema de coordenadas polares, construímos uma tabela de$r$ valores$\theta$ e. Nós inserimos valores de$\theta$ em uma equação polar e calculamos$r$. No entanto, usar as propriedades de simetria e encontrar os valores-chave de$\theta$ e$r$ significa que menos cálculos serão necessários.

Encontrando Zeros e Máxima

Para encontrar os zeros de uma equação polar, resolvemos os valores$\theta$ desse resultado em$r=0$. Lembre-se de que, para encontrar os zeros das funções polinomiais, definimos a equação igual a zero e depois resolvemos para$x$. Usamos o mesmo processo para equações polares. $r=0$Defina e resolva$\theta$.

Para muitas das formas que encontraremos, o valor máximo de uma equação polar é encontrado substituindo esses valores de$\theta$ na equação que resultam no valor máximo das funções trigonométricas. Considere$r=5 \cos \theta$; a distância máxima entre a curva e o pólo é de$5$ unidades. O valor máximo da função cosseno é$1$ quando$\theta=0$, então nossa equação polar é$5 \cos \theta$, e o valor$\theta=0$ produzirá o máximo$| r |$.

Da mesma forma, o valor máximo da função seno é$1$ quando$\theta=\dfrac{\pi}{2}$, e se nossa equação polar for$r=5 \sin \theta$, o valor$\theta=\dfrac{\pi}{2}$ produzirá o máximo$| r |$. Podemos encontrar informações adicionais calculando os valores de$r$ quando$\theta=0$. Esses pontos seriam interceptações do eixo polar, o que pode ser útil para desenhar o gráfico e identificar a curva de uma equação polar.

Exemplo$\PageIndex{2}$: Finding Zeros and Maximum Values for a Polar Equation

Usando a equação em Exemplo$\PageIndex{1}$, encontre os zeros e o máximo$| r |$ e, se necessário, o eixo polar intercepta de$r=2 \sin \theta$.

Solução

Para encontrar os zeros, defina$r$ igual a zero e resolva para$\theta$.

\[\begin{align*} 2 \sin \theta &= 0 \\ \sin \theta &= 0 \\ \theta &= {\sin}^{-1} 0 \\ \theta &= n\pi \qquad \text{where n is an integer} \end{align*}\]

Substitua qualquer um dos$\theta$ valores na equação. Nós usaremos$0$.

\[\begin{align*} r&= 2 \sin(0) \\ r&= 0 \end{align*}\]

Os pontos$(0,0)$ e$(0,\pm n\pi)$ são os zeros da equação. Todos eles coincidem, então apenas um ponto é visível no gráfico. Esse ponto também é a única interceptação do eixo polar.

Para encontrar o valor máximo da equação, observe o valor máximo da função trigonométrica$\sin \theta$, que ocorre quando$\theta=\dfrac{\pi}{2}\pm 2k\pi$ resulta em$\sin\left(\dfrac{\pi}{2}\right)=1$. Substituto$\dfrac{\pi}{2}$ para$\theta$.

\[\begin{align*} r&= 2 \sin\left(\dfrac{\pi}{2}\right) \\ r&= 2(1) \\ r&= 2 \end{align*}\]

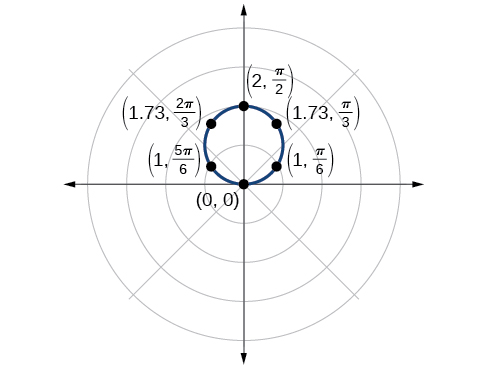
Análise

O ponto$\left(2,\dfrac{\pi}{2}\right)$ será o valor máximo no gráfico. Vamos traçar mais alguns pontos para verificar o gráfico de um círculo. Veja a tabela$\PageIndex{1}$ e a figura$\PageIndex{4}$.

Tabela$\PageIndex{1}$
$\theta$	$r=2 \sin \theta$	$r$
\ (\ theta\) ">$0$	\ (r=2\ sin\ theta\) ">$r=2 \sin(0)=0$	\ (r\) ">$0$
\ (\ theta\) ">$\dfrac{\pi}{6}$	\ (r=2\ sin\ theta\) ">$r=2 \sin\left(\dfrac{\pi}{6}\right)=1$	\ (r\) ">$1$
\ (\ theta\) ">$\dfrac{\pi}{3}$	\ (r=2\ sin\ theta\) ">$r=2 \sin\left(\dfrac{\pi}{3}\right)≈1.73$	\ (r\) ">$1.73$
\ (\ theta\) ">$\dfrac{pi}{2}$	\ (r=2\ sin\ theta\) ">$r=2 \sin\left(\dfrac{\pi}{2}\right)=2$	\ (r\) ">$2$
\ (\ theta\) ">$\dfrac{2\pi}{3}$	\ (r=2\ sin\ theta\) ">$r=2 \sin\left(\dfrac{2\pi}{3}\right)≈1.73$	\ (r\) ">$1.73$
\ (\ theta\) ">$\dfrac{5\pi}{6}$	\ (r=2\ sin\ theta\) ">$r=2 \sin\left(\dfrac{5\pi}{6}\right)=1$	\ (r\) ">$1$
\ (\ theta\) ">$\pi$	\ (r=2\ sin\ theta\) ">$r=2 \sin(\pi)=0$	\ (r\) ">$0$

Gráfico do círculo na grade de coordenadas polares. O centro está em (0,1) e tem raio 1. Seis pontos ao longo da circunferência estão marcados: (0,0), (1, pi/6), (1,3, pi/3), (2, pi/2), (1,73, 2pi/3) e (1, 5pi/6). — Figura$\PageIndex{4}$

Exercício$\PageIndex{2}$

Sem converter para coordenadas cartesianas, teste a simetria da equação dada e encontre os zeros e os valores máximos de$| r |$:$r=3 \cos \theta$.

Resposta: Os testes revelarão simetria sobre o eixo polar. O zero é$\left(0,\dfrac{\pi}{2}\right)$, e o valor máximo é$(3,0)$.

Investigando círculos

Agora vimos a equação de uma circunferência no sistema de coordenadas polares. Nos dois últimos exemplos, a mesma equação foi usada para ilustrar as propriedades da simetria e demonstrar como encontrar os zeros, os valores máximos e os pontos traçados que produziram os gráficos. No entanto, o círculo é apenas uma das muitas formas no conjunto de curvas polares.

Existem cinco curvas polares clássicas: cardióides, limaons, lemniscates, curvas de rosas e espirais de Arquimedes. Vamos abordar brevemente as fórmulas polares do círculo antes de passar para as curvas clássicas e suas variações.

FÓRMULAS PARA A EQUAÇÃO DE UMA CIRCUNFERÊNCIA

Algumas das fórmulas que produzem o gráfico de um círculo em coordenadas polares são dadas por$r=a \cos \theta$ e$r=a \sin \theta$, enquanto a é o diâmetro do círculo ou a distância do polo até o ponto mais distante da circunferência. O raio é$\dfrac{|a|}{2}$, ou metade, do diâmetro. Pois$r=a \cos \theta$, o centro é$\left(\dfrac{a}{2},0\right)$. Pois$r=a \sin \theta$, o centro é$\left(\dfrac{a}{2},\pi\right)$. A figura$\PageIndex{5}$ mostra os gráficos desses quatro círculos.

Quatro gráficos lado a lado. Todos têm um valor absoluto de raio de a/2. O primeiro é r=acos (theta), a — Figura$\PageIndex{5}$

Exemplo$\PageIndex{3}$: Sketching the Graph of a Polar Equation for a Circle

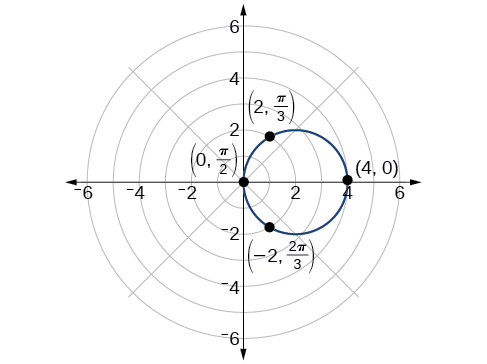
Esboce o gráfico de$r=4 \cos \theta$.

Solução

Primeiro, testando a equação para simetria, descobrimos que o gráfico é simétrico em relação ao eixo polar. Em seguida, encontramos os zeros e o máximo$| r |$ para$r=4 \cos \theta$. Primeiro$r=0$, defina e resolva$\theta$. Assim, um zero ocorre em$\theta=\dfrac{\pi}{2}\pm k\pi$. Um ponto chave para traçar é$\left(0,\dfrac{\pi}{2}\right)$.

Para encontrar o valor máximo de$r$, observe que o valor máximo da função cosseno é$1$ quando$\theta=0\pm 2k\pi$. $\theta=0$Substitua na equação:

\[\begin{align*} r&= 4 \cos \theta\\ r&= 4 \cos(0)\\ r&= 4(1)\\ &= 4 \end{align*}\]

O valor máximo da equação é$4$. Um ponto chave para traçar é$(4, 0)$.

Como$r=4 \cos \theta$ é simétrico em relação ao eixo polar, precisamos apenas calcular$r$ valores -para$θ$ o intervalo$[0, \pi]$. Os pontos no quadrante superior podem então ser refletidos no quadrante inferior. Faça uma tabela de valores semelhante à Tabela$\PageIndex{2}$. O gráfico é mostrado na Figura$\PageIndex{6}$.

Tabela$\PageIndex{2}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{3\pi}{4}$	$\dfrac{5\pi}{6}$	$\pi$
$r$	$4$	$3.46$	$2.83$	$2$	$0$	$−2$	$−2.83$	$−3.46$	$4$

Gráfico de 4=4cos (teta) em coordenadas polares. Os pontos (0, pi/2), (-2, 2pi/3), (4,0) e (2, pi/3) estão marcados na circunferência. — Figura$\PageIndex{6}$

Investigando cardióides

Embora a tradução de coordenadas polares para coordenadas cartesianas possa parecer mais simples em alguns casos, representar graficamente as curvas clássicas é, na verdade, menos complicado no sistema polar. A próxima curva é chamada de cardióide, pois se assemelha a um coração. Essa forma geralmente é incluída na família de curvas chamadas limaçons, mas aqui discutiremos o cardióide por si só.

FÓRMULAS PARA UM CARDIÓIDE

As fórmulas que produzem os gráficos de um cardióide são dadas por$r=a\pm b \cos \theta$ e$r=a\pm b \sin \theta$ onde$a>0$$b>0$,$\dfrac{a}{b}=1$ e. O gráfico cardióide passa pelo pólo, como podemos ver na Figura$\PageIndex{7}$.

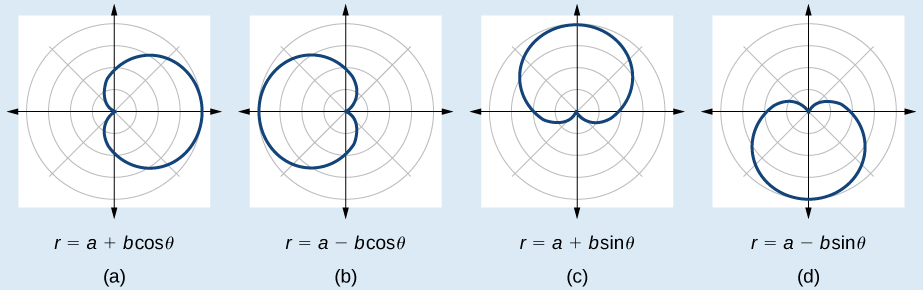
Gráfico de quatro cardióides. (A) é r = a + bcos (teta). Cardioide se estendendo para a direita. (B) é r=a-bcos (teta). Cardioide se estendendo para a esquerda. (C) é r=a+bsin (teta). Cardioide se estendendo. (D) é r=a-bsin (teta). Cardioide se estendendo para baixo. — Figura$\PageIndex{7}$

Como: Dada a equação polar de um cardióide, esboce seu gráfico

Verifique a equação para os três tipos de simetria.
Encontre os zeros. Conjunto$r=0$.
Encontre o valor máximo da equação de acordo com o valor máximo da expressão trigonométrica.
Faça uma tabela de valores para$r$$\theta$ e.
Faça um gráfico dos pontos e desenhe o gráfico.

Exemplo$\PageIndex{4}$: Sketching the Graph of a Cardioid

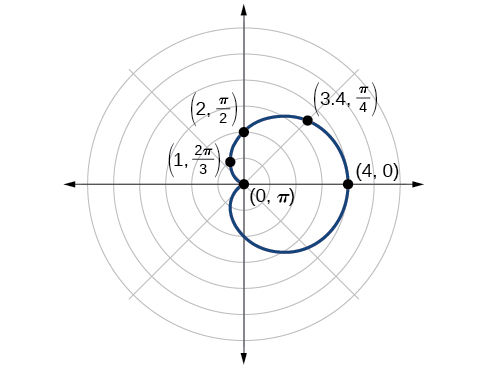
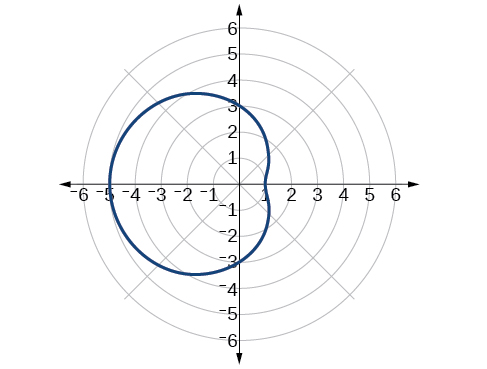
Esboce o gráfico de$r=2+2 \cos \theta$.

Solução

Primeiro, testando a equação para simetria, descobrimos que o gráfico dessa equação será simétrico em relação ao eixo polar. Em seguida, encontramos os zeros e os máximos. Configuração$r=0$, nós temos$\theta=\pi+2k\pi$. O zero da equação está localizado em$(0,\pi)$. O gráfico passa por esse ponto.

O valor máximo de$r=2+2 \cos \theta$ ocorre quando$\cos \theta$ é um máximo, que é quando$\cos \theta=1$ ou quando$\theta=0$. Substitua$\theta=0$ na equação e resolva$r$.

\[\begin{align*} r&= 2+2 \cos(0)\\ r&= 2+2(1)\\ &= 4 \end{align*}\]

O ponto$(4,0)$ é o valor máximo no gráfico.

Descobrimos que a equação polar é simétrica em relação ao eixo polar, mas como ela se estende aos quatro quadrantes, precisamos traçar valores ao longo do intervalo$[0, \pi]$. A parte superior do gráfico é então refletida sobre o eixo polar. Em seguida, fazemos uma tabela de valores, como na Tabela$\PageIndex{3}$, e depois traçamos os pontos e desenhamos o gráfico. Veja a Figura$\PageIndex{8}$.

Tabela$\PageIndex{3}$
θ	0	$\dfrac{π}{4}$	$\dfrac{π}{2}$	$\dfrac{2π}{3}$	$π$
r	4	3,41	2	1	0

Gráfico de r=2+2cos (teta). Cardioide se estendendo para a direita. Os pontos na borda (0, pi), (4,0), (3.4, pi/4), (2, pi/2) e (1, 2pi/3) são mostrados. — Figura$\PageIndex{8}$

Investigando Limaçons

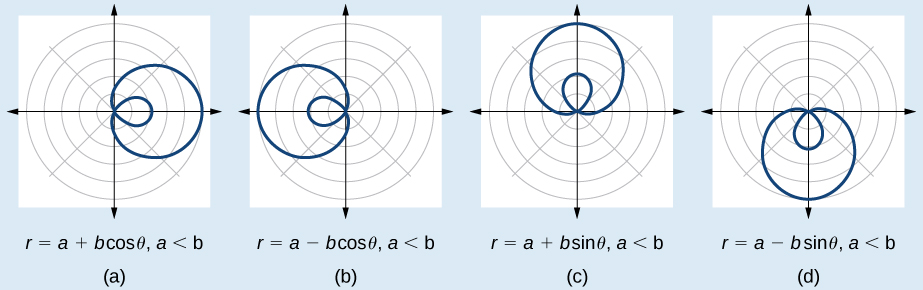
A palavra limaçon significa “caracol” em francês antigo, um nome que descreve a forma do gráfico. Como mencionado anteriormente, o cardióide é membro da família limaçon, e podemos ver as semelhanças nos gráficos. As outras imagens nesta categoria incluem o limaçon de um loop e o limaçon de dois loops (ou loop interno). Limaçons de um loop às vezes são chamados de limaçons com covinhas quando$1<\dfrac{a}{b}<2$ e limaçons convexos quando$\dfrac{a}{b}≥2$.

FÓRMULAS PARA LIMAÇONS DE UM ÚNICO CICLO

As fórmulas que produzem o gráfico de um limaçon de um loop com covinhas são dadas por$r=a\pm b \cos \theta$ e$r=a\pm b \sin \theta$ onde$a>0$$b>0$,$1<ab<2$ e. Todos os quatro gráficos são mostrados na Figura$\PageIndex{9}$.

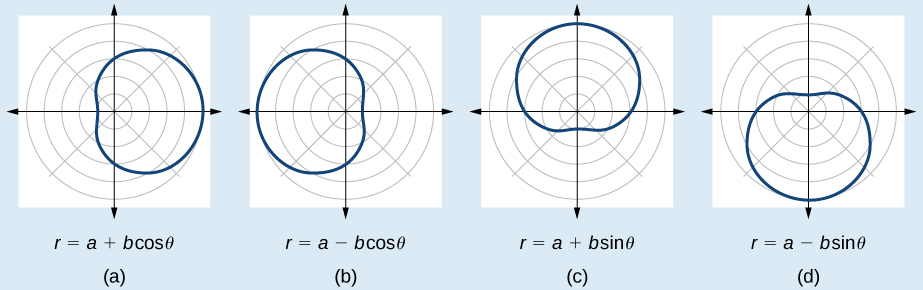
Quatro limaçons com covinhas lado a lado. (A) é r=a+bcos (teta). Estendendo-se para a direita. (B) é r=a-bcos (teta). Estendendo-se para a esquerda. (C) é r=a+bsin (teta). Estendendo-se até. (D) é r=a-bsin (teta). Estendendo-se para baixo. — Figura$\PageIndex{9}$

Como: Dada uma equação polar para um limaçon de um loop, esboce o gráfico

Teste a equação quanto à simetria. Lembre-se de que falhar em um teste de simetria não significa que a forma não exibirá simetria. Muitas vezes, a simetria pode se revelar quando os pontos são traçados.
Encontre os zeros.
Encontre os valores máximos de acordo com a expressão trigonométrica.
Faça uma mesa.
Faça um gráfico dos pontos e desenhe o gráfico.

Exemplo$\PageIndex{5}$: Sketching the Graph of a One-Loop Limaçon

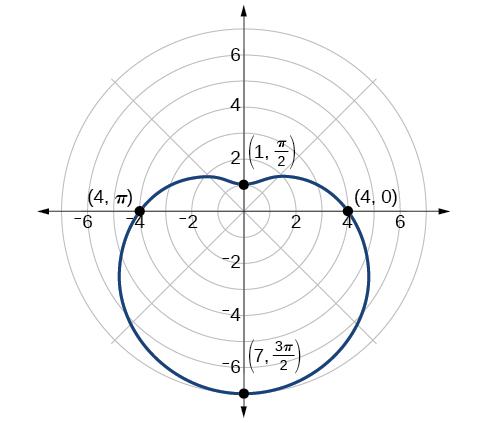
Faça um gráfico da equação$r=4−3 \sin \theta$.

Solução

Primeiro, testando a equação para simetria, descobrimos que ela falha em todos os três testes de simetria, o que significa que o gráfico pode ou não exibir simetria, então não podemos usar a simetria para nos ajudar a representar graficamente. No entanto, essa equação tem um gráfico que mostra claramente a simetria em relação à linha$\theta=\dfrac{\pi}{2}$, mas falha em todos os três testes de simetria. Uma calculadora gráfica ilustrará imediatamente a qualidade reflexiva do gráfico.

Em seguida, encontramos os zeros e o máximo e traçamos os pontos refletores para verificar qualquer simetria. A configuração$r=0$ resulta em$\theta$ ser indefinida. O que isso significa? Como poderia$\theta$ ser indefinido? O ângulo$\theta$ é indefinido para qualquer valor de$\sin \theta>1$. Portanto,$\theta$ é indefinido porque não há valor de$\theta$ para qual$\sin \theta>1$. Consequentemente, o gráfico não passa pelo polo. Talvez o gráfico cruze o eixo polar, mas não no polo. Podemos investigar outras interceptações calculando$r$ quando$\theta=0$.

\[\begin{align*} r(0)&= 4-3 \sin(0)\\ r&= 4-3\cdot 0\\ &= 4 \end{align*}\]

Portanto, há pelo menos uma interceptação do eixo polar em$(4,0)$.

Em seguida, como o valor máximo da função seno é$1$ quando$\theta=\dfrac{\pi}{2}$, substituiremos$\theta=\dfrac{\pi}{2}$ a equação e resolveremos$r$. Assim,$r=1$.

Faça uma tabela das coordenadas semelhante à Tabela$\PageIndex{4}$.

Tabela$\PageIndex{4}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{11\pi}{6}$	$2\pi$
$r$	$4$	$2.5$	$1.4$	$1$	$1.4$	$2.5$	$4$	$5.5$	$6.6$	$7$	$6.6$	$5.5$	$4$

O gráfico é mostrado na Figura$\PageIndex{10}$.

Gráfico do limaçon r=4-3sin (teta). Estendendo-se para baixo. Os pontos na borda são mostrados: (1, pi/2), (4,0), (4, pi) e (7, 3pi/2). — Figura$\PageIndex{10}$: Limaçon de um laço

Análise

Este é um exemplo de curva para a qual criar uma tabela de valores é fundamental para produzir um gráfico preciso. Os testes de simetria falham; o zero é indefinido. Embora possa ser evidente que uma equação envolvida$\sin \theta$ é provavelmente simétrica em relação à linha$\theta=\dfrac{\pi}{2}$, avaliar mais pontos ajuda a verificar se o gráfico está correto.

Exercício$\PageIndex{3}$

Esboce o gráfico de$r=3−2 \cos \theta$.

Resposta: $Gráfico do limaçon r=3-2cos (theta). Estendendo-se para a esquerda.$
Figura$\PageIndex{11}$

Outro tipo de limaçon, o limaçon de laço interno, tem o nome do laço formado dentro da forma geral de limaçon. Foi descoberto pelo artista alemão Albrecht Dürer (1471-1528), que revelou um método para desenhar o limaçon de circuito interno em seu livro Underweysung der Messing, de 1525. Um século depois, o pai do matemático Blaise Pascal, Étienne Pascal (1588-1651), a redescobriu.

FÓRMULAS PARA LIMAÇONS DE CIRCUITO INTERNO

As fórmulas que geram os limaçons do circuito interno são dadas por$r=a\pm b\cos \theta$ e$r=a\pm b \sin \theta$ onde$a>0$$b>0$,$a<b$ e. O gráfico do limaçon do circuito interno passa pelo pólo duas vezes: uma para o laço externo e outra para o laço interno. Consulte a Figura 10.5.12 para ver os gráficos.

Gráfico de quatro limaçons de laço interno lado a lado. (A) é r=a+bcos (teta), a<b. Estendido para a direita. (B) é a-bcos (teta), a<b. Estende-se para a esquerda. (C) é r=a+bsin (teta), a<b. Estende-se para cima. (D) é r=a-bsin (teta), a<b. Estende-se para baixo. — Figura$\PageIndex{12}$

Exemplo$\PageIndex{6}$: Sketching the Graph of an Inner-Loop Limaçon

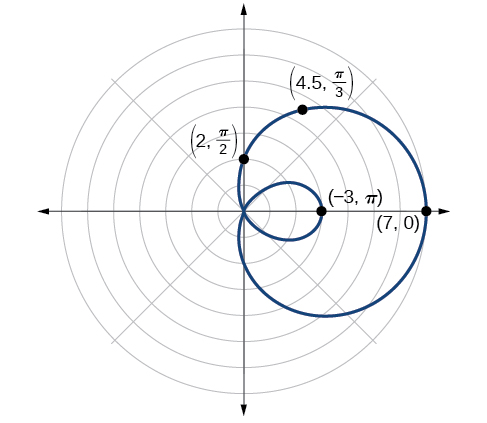
Esboce o gráfico de$r=2+5 \cos \theta$.

Solução

Testando a simetria, descobrimos que o gráfico da equação é simétrico em relação ao eixo polar. Em seguida, encontrar os zeros revela que quando$r=0$,$\theta=1.98$. O máximo$| r |$ é encontrado quando$\cos \theta=1$ ou quando$\theta=0$. Assim, o máximo é encontrado no ponto$(7, 0)$.

Embora tenhamos encontrado a simetria, o zero e o máximo, traçar mais pontos ajudará a definir a forma e, em seguida, um padrão surgirá. Veja a tabela$\PageIndex{5}$.

Tabela$\PageIndex{5}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{11\pi}{6}$	$2\pi$
$r$	$7$	$6.3$	$4.5$	$2$	$−0.5$	$−2.3$	$−3$	$−2.3$	$−0.5$	$2$	$4.5$	$6.3$	$7$

Como esperado, os valores começam a se repetir depois$\theta=\pi$. O gráfico é mostrado na Figura$\PageIndex{13}$.

Gráfico do circuito interno limaçon r=2+5cos (teta). Estende-se para a direita. Os pontos na borda traçada são (7,0), (4,5, pi/3), (2, pi/2) e (-3, pi). — Figura$\PageIndex{13}$: Limação de circuito interno

Investigando Lemniscates

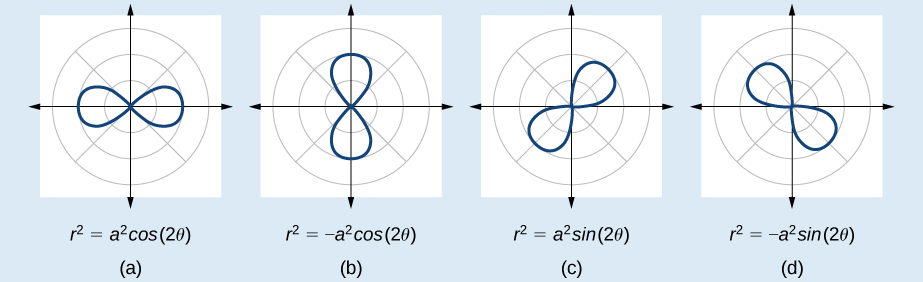
O lemniscado é uma curva polar semelhante ao símbolo do infinito$\infty$ ou a uma figura$8$. Centralizado no polo, um lemniscado é simétrico por definição.

FÓRMULAS PARA LEMNISCATES

As fórmulas que geram o gráfico de um lemniscado são dadas por$r^2=a^2 \cos 2\theta$ e$r^2=a^2 \sin 2\theta$ onde$a≠0$. A fórmula$r^2=a^2 \sin 2\theta$ é simétrica em relação ao polo. A fórmula$r^2=a^2 \cos 2\theta$ é simétrica em relação ao polo, à linha$\theta=\dfrac{\pi}{2}$ e ao eixo polar. Veja a Figura$\PageIndex{14}$ para ver os gráficos.

Quatro gráficos de lemniscados lado a lado. (A) é r^2 = a^2 * cos (2theta). Figura horizontal oito, no eixo x. (B) é r^2 = - a^2 * cos (2theta). Figura vertical oito, no eixo y. (C) é r^2 = a^2 * sin (2theta). A figura diagonal oito na linha y=x. (D) é r^2 = -a^2 *sin (2theta). Figura diagonal oito na linha y=-x. — Figura$\PageIndex{14}$

Exemplo$\PageIndex{7}$: Sketching the Graph of a Lemniscate

Esboce o gráfico de$r^2=4 \cos 2\theta$.

Solução

A equação apresenta simetria em relação à linha$\theta=\dfrac{\pi}{2}$, ao eixo polar e ao polo.

Vamos encontrar os zeros. Já deveria ser rotina, mas abordaremos essa equação de forma um pouco diferente fazendo a substituição$u=2\theta$.

\[\begin{align*} 0 &= 4 \cos 2\theta \\ 0 &= 4 \cos u \\ 0 &= \cos u \\ {\cos}^{-1} 0 &= \dfrac{\pi}{2} \\ u &= \dfrac{\pi}{2} \qquad \text{Substitute } 2\theta \text{ back in for } u. \\ 2\theta &= \dfrac{\pi}{2} \\ \theta &= \dfrac{\pi}{4} \end{align*}\]

Então, o ponto$\left(0,\dfrac{\pi}{4}\right)$ é um zero da equação.

Agora vamos encontrar o valor máximo. Desde o máximo de$\cos u=1$ quando$u=0$, o máximo$\cos 2\theta=1$ quando$2\theta=0$. Assim,

\[\begin{align*} r^2 &= 4 \cos(0) \\ r^2 &= 4(1)\\ r^2&= 4 \\ r&= \pm 4\\ &=2 \end{align*}\]

Temos um máximo em$(2, 0)$. Como esse gráfico é simétrico em relação ao polo, à linha$\theta=\dfrac{\pi}{2}$ e ao eixo polar, precisamos apenas traçar pontos no primeiro quadrante.

Faça uma tabela semelhante à Tabela$\PageIndex{6}$.

Tabela$\PageIndex{6}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$
$r$	$2$	$\sqrt{2}$	$0$	$\sqrt{2}$	$0$

Faça um gráfico dos pontos no gráfico, como o mostrado na Figura$\PageIndex{15}$.

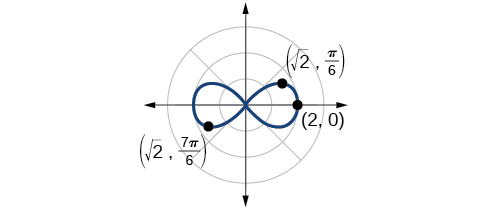
Gráfico de r^2 = 4cos (2theta). Lemniscado horizontal, ao longo do eixo x. Os pontos na borda traçada são (2,0), (rad2, pi/6), (rad2 7pi/6). — Figura$\PageIndex{15}$: Lemniscate

Análise

Fazer uma substituição como essa$u=2\theta$ é uma prática comum em matemática porque pode simplificar os cálculos. No entanto, não devemos esquecer de substituir o termo de substituição pelo termo original no final e depois resolver o desconhecido.

Alguns dos pontos neste gráfico podem não aparecer usando a função Trace na calculadora gráfica TI-84, e a tabela da calculadora pode mostrar um erro para esses mesmos pontos de$r$. Isso ocorre porque não há raízes quadradas reais para esses valores de$θ$. Em outras palavras, os$r$ valores -correspondentes de$\sqrt{4 \cos(2\theta)}$ são números complexos porque há um número negativo sob o radical.

Investigando curvas de rosas

O próximo tipo de equação polar produz uma forma semelhante a uma pétala chamada curva de rosa. Embora os gráficos pareçam complexos, uma equação polar simples gera o padrão.

CURVAS DE ROSAS

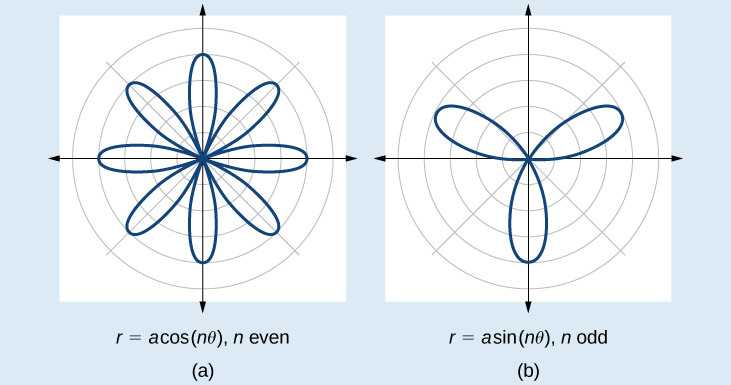
As fórmulas que geram o gráfico de uma curva de rosas são dadas por$r=a \cos n\theta$ e$r=a \sin n\theta$ onde$a≠0$. Se$n$ for uniforme, a curva tem$2n$ pétalas. Se$n$ for estranho, a curva tem$n$ pétalas. Veja a Figura$\PageIndex{16}$.

Exemplo$\PageIndex{8}$: Sketching the Graph of a Rose Curve ($n$ Even)

Esboce o gráfico de$r=2 \cos 4\theta$.

Solução

Testando a simetria, descobrimos novamente que os testes de simetria não contam toda a história. O gráfico não é apenas simétrico em relação ao eixo polar, mas também em relação à linha$\theta=\dfrac{\pi}{2}$ e ao polo.

Agora vamos encontrar os zeros. Primeiro faça a substituição$u=4\theta$.

\[\begin{align*} 0 &= 2 \cos 4\theta \\ 0 &= \cos 4\theta \\ 0 &= \cos u \\ {\cos}^{-1} 0 &=u \\ u &= \dfrac{\pi}{2} \\ 4\theta &= \dfrac{\pi}{2} \\ \theta &=\dfrac{\pi}{8} \end{align*}\]

O zero é$\theta=\dfrac{\pi}{8}$. O ponto$\left(0,\dfrac{\pi}{8}\right)$ está na curva.

Em seguida, encontramos o máximo$| r |$. Sabemos que o valor máximo de$\cos u=1$ quando$\theta=0$. Assim,

\[\begin{align*} r &=2 \cos(4\cdot 0) \\ r &=2 \cos(0) \\ r &=2(1)\\ &= 2 \end{align*}\]

O ponto$(2,0)$ está na curva.

O gráfico da curva rosa tem propriedades únicas, que são reveladas na Tabela$\PageIndex{7}$.

Tabela$\PageIndex{7}$
$\theta$	$0$	$\dfrac{\pi}{8}$	$\dfrac{\pi}{4}$	$\dfrac{3\pi}{8}$	$\dfrac{\pi}{2}$	$5π8$	$3π4$
$r$	$2$	$0$	$−2$	$0$	$2$	$0$	$−2$

Como$r=0$ quando$\theta=\dfrac{\pi}{8}$, faz sentido dividir os valores na tabela por$\dfrac{\pi}{8}$ unidades. Surge um padrão definido. Veja o intervalo de$r$ valores -:$2, 0, −2, 0$ e assim por diante. Isso representa o desenvolvimento da curva, uma pétala por vez. Começando em$r=0$, cada pétala se estende por uma distância de e depois volta para zero$2n$ vezes$r=2$, totalizando oito pétalas. Veja o gráfico na Figura$\PageIndex{17}$.

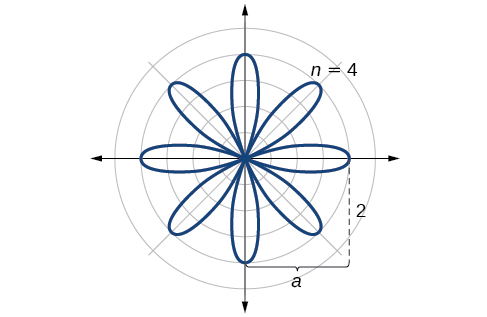
Esboço da curva de rosas r=2*cos (4 teta). Extrai uma distância de 2 para cada pétala 2n vezes (aqui 2*4 = 8 vezes). — Figura$\PageIndex{17}$: Curva de rosas,$n$ uniforme

Análise

Quando essas curvas são desenhadas, é melhor traçar os pontos em ordem, como na tabela$\PageIndex{7}$. Isso nos permite ver como o gráfico atinge o máximo (a ponta de uma pétala), volta cruzando o poste, atinge o máximo oposto e volta ao poste. A ação é contínua até que todas as pétalas sejam desenhadas.

Exercício$\PageIndex{4}$

Esboce o gráfico de$r=4 \sin(2\theta)$.

Resposta: O gráfico é uma curva de rosas,$n$ uniforme

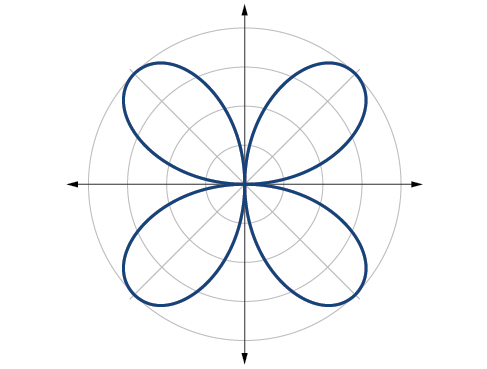
$Gráfico da curva de rosas r=4 sin (2 teta). Par - quatro pétalas igualmente espaçadas, cada uma com 4 de comprimento.$
Figura$\PageIndex{18}$

Exemplo$\PageIndex{9}$: Sketching the Graph of a Rose Curve ($n$ Odd)

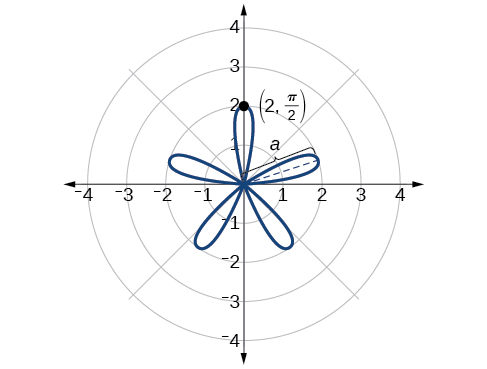
Esboce o gráfico de$r=2 \sin(5\theta)$.

Solução

O gráfico da equação mostra simetria em relação à linha$\theta=\dfrac{\pi}{2}$. Em seguida, encontre os zeros e o máximo. Queremos fazer a substituição$u=5\theta$.

\[\begin{align*} 0 &=2 \sin(5\theta) \\ 0 &=\sin u \\ {\sin}^{-1} 0 &=0 \\ u &=0 \\ 5\theta &=0 \\ \theta &=0 \end{align*}\]

O valor máximo é calculado no ângulo em que$\sin \theta$ é o máximo. Portanto,

\[\begin{align*} r&= 2 \sin\left(5\cdot \dfrac{\pi}{2}\right) \\ r&= 2(1)\\ &= 2 \end{align*}\]

Assim, o valor máximo da equação polar é$2$. Esse é o comprimento de cada pétala. Como a curva$n$ ímpar produz o mesmo número de pétalas$n$, haverá cinco pétalas no gráfico. Veja a Figura$\PageIndex{19}$.

Crie uma tabela de valores semelhante à Tabela$\PageIndex{8}$.

Tabela$\PageIndex{8}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$
$r$	\ (0\ 0)	$1$	$−1.73$	$2$	$−1.73$	$1$	$0$

Gráfico da curva de rosas r=2sin (5theta). Cinco pétalas igualmente espaçadas em torno da origem. O ponto (2, pi/2) na borda está marcado. — Figura$\PageIndex{19}$: Curva de rosas,$n$ ímpar

Exercício$\PageIndex{5}$

Esboce o gráfico de$r=3 \cos(3\theta)$.

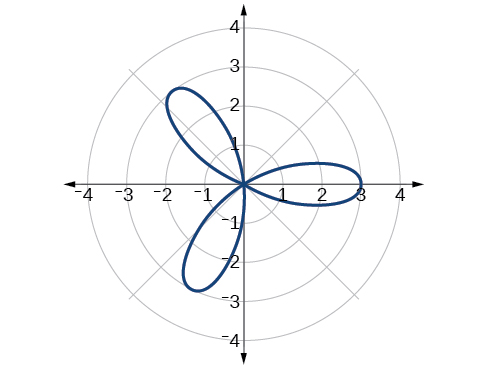
Resposta: $Gráfico da curva de rosas r=3cos (3theta). Três pétalas igualmente espaçadas da origem.$
Figura$\PageIndex{20}$

Curva rosa,$n$ ímpar

Investigando a espiral de Arquimedes

A equação polar final que discutiremos é a espiral de Arquimedes, nomeada em homenagem ao seu descobridor, o matemático grego Arquimedes (c. 287 AEC - c. 212 AEC), que é creditado com inúmeras descobertas nas áreas de geometria e mecânica.

A ESPIRAL DE ARQUIMEDES

A fórmula que gera o gráfico da espiral de Arquimedes é dada$r=\theta$ por for$\theta≥0$. À medida que$\theta$$r$ aumenta, aumenta a uma taxa constante em um caminho cada vez maior, sem fim e em espiral. Veja a Figura$\PageIndex{21}$.

Como: Dada a espiral de Arquimedes$[ 0,2\pi ]$,sketch the graph

Faça uma tabela de valores para$r$ e$\theta$ sobre o domínio fornecido.
Faça um gráfico dos pontos e desenhe o gráfico.

Exemplo$\PageIndex{10}$: Sketching the Graph of an Archimedes’ Spiral

Esboce o gráfico de$r=\theta$ over$[0,2\pi]$.

Solução

Como$r$ é igual a$\theta$, o gráfico da espiral de Arquimedes começa no pólo no ponto$(0, 0)$. Embora o gráfico indique simetria, não há simetria formal em relação à aprovação nos testes de simetria. Além disso, não há valor máximo, a menos que o domínio seja restrito.

Crie uma tabela como Tabela$\PageIndex{9}$.

Tabela$\PageIndex{9}$
$\theta$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$	$0.785$	$1.57$	$3.14$	$4.71$	$5.50$	$6.28$

Observe que os valores r são apenas a forma decimal do ângulo medido em radianos. Podemos vê-los em um gráfico na Figura$\PageIndex{22}$.

Gráfico da espiral de Arquimedes r=teta sobre [0,2pi]. Começa na origem e sai em espiral em um loop no sentido anti-horário. Os pontos (pi/4, pi/4), (pi/2, pi/2), (pi, pi), (5pi/4, 5pi/4), (7pi/4, pi/4) e (2pi, 2pi) estão marcados. — Figura$\PageIndex{22}$: A espiral de Arquimedes

Análise

O domínio dessa curva polar é$[ 0,2\pi ]$. Em geral, entretanto, o domínio dessa função é$(−\infty,\infty)$. Representar graficamente a equação da espiral de Arquimedes é bastante simples, embora a imagem pareça complexa.

Exercício$\PageIndex{6}$

Esboce o gráfico de$r=−\theta$ over the interval$[ 0,4\pi ]$.

Resposta: $alt$
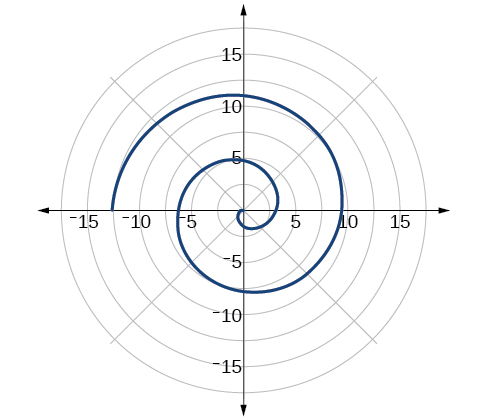
Figura$\PageIndex{23}$

Resumo das curvas

Nós exploramos várias curvas polares aparentemente complexas nesta seção. A figura$\PageIndex{24}$ e a figura$\PageIndex{25}$ resumem os gráficos e equações para cada uma dessas curvas.

Quatro gráficos lado a lado - um resumo. (A) é um círculo: r=asin (theta) ou r=acos (theta). (B) é um cardióide: r= a + ou - bcos (teta), ou r = a + ou - b sin (teta). a — Figura$\PageIndex{24}$

Quatro gráficos lado a lado - um resumo. (A) é leniscates. R^2 = a^2cos (2theta) ou r^2=a^2sin (2theta). a não é igual a 0. (B) é uma curva de rosa (um par). R = acos (ntheta) ou r=asin (ntheta). N é par e há 2n pétalas. (C) é uma curva de rosas (n ímpar). R = acos (ntheta) ou r=asin (teta). N é estranho e não há pétalas. (D) é uma espiral de Arquimedes. r=teta e teta — Figura$\PageIndex{25}$

Mídia

Acesse esses recursos on-line para obter instruções e práticas adicionais com gráficos de coordenadas polares.

Representação gráfica de equações polares, parte 1
Representação gráfica de equações polares, parte 2
Animação: Os gráficos das equações polares
Representação gráfica de equações polares no TI-84

Conceitos-chave

É mais fácil representar graficamente as equações polares se pudermos testar a simetria das equações em relação à linha$\theta=\dfrac{\pi}{2}$, ao eixo polar ou ao polo.
Existem três testes de simetria que indicam se o gráfico de uma equação polar exibirá simetria. Se uma equação falhar em um teste de simetria, o gráfico pode ou não exibir simetria. Veja o exemplo$\PageIndex{1}$.
As equações polares podem ser representadas graficamente fazendo uma tabela de valores para$\theta$$r$ e.
O valor máximo de uma equação polar é encontrado substituindo o valor$\theta$ que leva ao valor máximo da expressão trigonométrica.
Os zeros de uma equação polar são encontrados definindo$r=0$ e resolvendo para$\theta$. Veja o exemplo$\PageIndex{2}$.
Algumas fórmulas que produzem o gráfico de um círculo em coordenadas polares são dadas por$r=a \cos \theta$$r=a \sin \theta$ e. Veja o exemplo$\PageIndex{3}$.
As fórmulas que produzem os gráficos de um cardióide são dadas por$r=a\pm b \cos \theta$ e$r=a\pm b \sin \theta$$a>0$, para$b>0$,$ab=1$ e. Veja o exemplo$\PageIndex{4}$.
As fórmulas que produzem os gráficos de um limaçon de um loop são dadas por$r=a\pm b \cos \theta$ e$r=a\pm b \sin \theta$ para$1<ab<2$. Veja o exemplo$\PageIndex{5}$.
As fórmulas que produzem os gráficos de um limaçon de circuito interno são dadas$r=a\pm b \sin \theta$ por$r=a\pm b \cos \theta$ e para$a>0$$b>0$,$a<b$ e. Veja o exemplo$\PageIndex{6}$.
As fórmulas que produzem os gráficos de um lemniscates são dadas por$r^2=a^2 \cos 2\theta$ e$r^2=a^2 \sin 2\theta$, onde$a≠0$ .Veja o exemplo$\PageIndex{7}$.
As fórmulas que produzem os gráficos das curvas das rosas são dadas por$r=a \cos n\theta$ e$r=a \sin n\theta$, onde$a≠0$; se$n$ for par, há$2n$ pétalas e, se$n$ for ímpar, não há pétalas. Veja o exemplo$\PageIndex{8}$ e o exemplo$\PageIndex{9}$.
A fórmula que produz o gráfico da espiral de Arquimedes é dada por$r=\theta$,$\theta≥0$. Veja o exemplo$\PageIndex{10}$.

\(\theta\)	\(r=2 \sin \theta\)	\(r\)
\ (\ theta\) ">\(0\)	\ (r=2\ sin\ theta\) ">\(r=2 \sin(0)=0\)	\ (r\) ">\(0\)
\ (\ theta\) ">\(\dfrac{\pi}{6}\)	\ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{6}\right)=1\)	\ (r\) ">\(1\)
\ (\ theta\) ">\(\dfrac{\pi}{3}\)	\ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{3}\right)≈1.73\)	\ (r\) ">\(1.73\)
\ (\ theta\) ">\(\dfrac{pi}{2}\)	\ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{2}\right)=2\)	\ (r\) ">\(2\)
\ (\ theta\) ">\(\dfrac{2\pi}{3}\)	\ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{2\pi}{3}\right)≈1.73\)	\ (r\) ">\(1.73\)
\ (\ theta\) ">\(\dfrac{5\pi}{6}\)	\ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{5\pi}{6}\right)=1\)	\ (r\) ">\(1\)
\ (\ theta\) ">\(\pi\)	\ (r=2\ sin\ theta\) ">\(r=2 \sin(\pi)=0\)	\ (r\) ">\(0\)

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{3\pi}{4}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)
\(r\)	\(4\)	\(3.46\)	\(2.83\)	\(2\)	\(0\)	\(−2\)	\(−2.83\)	\(−3.46\)	\(4\)

θ	0	\(\dfrac{π}{4}\)	\(\dfrac{π}{2}\)	\(\dfrac{2π}{3}\)	\(π\)
r	4	3,41	2	1	0

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)	\(\dfrac{7\pi}{6}\)	\(\dfrac{4\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{5\pi}{3}\)	\(\dfrac{11\pi}{6}\)	\(2\pi\)
\(r\)	\(4\)	\(2.5\)	\(1.4\)	\(1\)	\(1.4\)	\(2.5\)	\(4\)	\(5.5\)	\(6.6\)	\(7\)	\(6.6\)	\(5.5\)	\(4\)

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)	\(\dfrac{7\pi}{6}\)	\(\dfrac{4\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{5\pi}{3}\)	\(\dfrac{11\pi}{6}\)	\(2\pi\)
\(r\)	\(7\)	\(6.3\)	\(4.5\)	\(2\)	\(−0.5\)	\(−2.3\)	\(−3\)	\(−2.3\)	\(−0.5\)	\(2\)	\(4.5\)	\(6.3\)	\(7\)

Nota: TESTES DE SIMETRIA

Como fazer: Dada uma equação polar, teste a simetria.

Exemplo\(\PageIndex{1}\): Testing a Polar Equation for Symmetry

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\): Finding Zeros and Maximum Values for a Polar Equation

Exercício\(\PageIndex{2}\)

Investigando círculos

FÓRMULAS PARA A EQUAÇÃO DE UMA CIRCUNFERÊNCIA

Exemplo\(\PageIndex{3}\): Sketching the Graph of a Polar Equation for a Circle

Investigando cardióides

FÓRMULAS PARA UM CARDIÓIDE

Como: Dada a equação polar de um cardióide, esboce seu gráfico

Exemplo\(\PageIndex{4}\): Sketching the Graph of a Cardioid

Investigando Limaçons

FÓRMULAS PARA LIMAÇONS DE UM ÚNICO CICLO

Como: Dada uma equação polar para um limaçon de um loop, esboce o gráfico

Exemplo\(\PageIndex{5}\): Sketching the Graph of a One-Loop Limaçon

Exercício\(\PageIndex{3}\)

FÓRMULAS PARA LIMAÇONS DE CIRCUITO INTERNO

Exemplo\(\PageIndex{6}\): Sketching the Graph of an Inner-Loop Limaçon

Investigando Lemniscates

FÓRMULAS PARA LEMNISCATES

Exemplo\(\PageIndex{7}\): Sketching the Graph of a Lemniscate

Investigando curvas de rosas

CURVAS DE ROSAS

Exemplo\(\PageIndex{8}\): Sketching the Graph of a Rose Curve (\(n\) Even)

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{9}\): Sketching the Graph of a Rose Curve (\(n\) Odd)

Exercício\(\PageIndex{5}\)

Investigando a espiral de Arquimedes

A ESPIRAL DE ARQUIMEDES

Como: Dada a espiral de Arquimedes\([ 0,2\pi ]\),sketch the graph

Exemplo\(\PageIndex{10}\): Sketching the Graph of an Archimedes’ Spiral

Exercício\(\PageIndex{6}\)

Mídia

\(\theta\)	\(0\)	\(\dfrac{\pi}{8}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{3\pi}{8}\)	\(\dfrac{\pi}{2}\)	\(5π8\)	\(3π4\)
\(r\)	\(2\)	\(0\)	\(−2\)	\(0\)	\(2\)	\(0\)	\(−2\)

Tabela\(\PageIndex{9}\)
\(\theta\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{2}\)	\(\pi\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{7\pi}{4}\)	\(2\pi\)
\(r\)	\(0.785\)	\(1.57\)	\(3.14\)	\(4.71\)	\(5.50\)	\(6.28\)