8.3: Coordenadas polares
- Page ID
- 189135
- Faça um gráfico de pontos usando coordenadas polares.
- Converta de coordenadas polares em coordenadas retangulares.
- Converta de coordenadas retangulares em coordenadas polares.
- Transforme equações entre formas polares e retangulares.
- Identifique e represente graficamente equações polares convertendo-as em equações retangulares.
A\(12\) quilômetros do porto, um veleiro enfrenta condições climáticas adversas e é levado para fora do curso por um vento\(16\) de um nó (veja a Figura\(\PageIndex{1}\)). Como o marinheiro pode indicar sua localização para a Guarda Costeira? Nesta seção, investigaremos um método de representação de localização que é diferente de uma grade de coordenadas padrão.
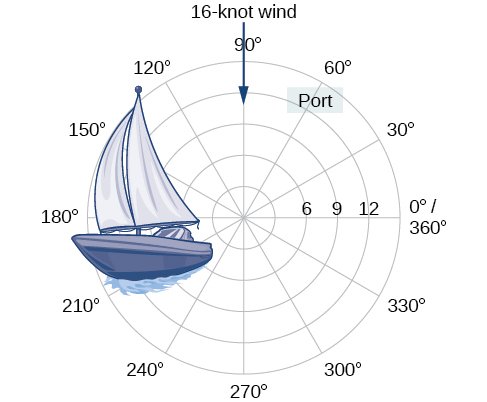
Figura\(\PageIndex{1}\)
Traçar pontos usando coordenadas polares
Quando pensamos em traçar pontos no plano, geralmente pensamos\((x,y)\) em coordenadas retangulares no plano de coordenadas cartesiano. No entanto, existem outras formas de escrever um par de coordenadas e outros tipos de sistemas de grade. Nesta seção, apresentamos as coordenadas polares, que são pontos rotulados\((r,\theta)\) e plotados em uma grade polar. A grade polar é representada como uma série de círculos concêntricos que se irradiam do polo ou a origem do plano coordenado.
A grade polar é dimensionada como o círculo unitário com o eixo positivo\(x\) agora visto como o eixo polar e a origem como o polo. A primeira coordenada\(r\) é o raio ou o comprimento do segmento de linha direcionado do polo. O ângulo\(\theta\), medido em radianos, indica a direção de\(r\). Nós nos movemos no sentido anti-horário a partir do eixo polar em um ângulo de\(\theta\), e medimos um segmento de linha direcionado com o comprimento de\(r\) na direção de\(\theta\). Mesmo que meçamos\(\theta\) primeiro e depois\(r\), o ponto polar é escrito primeiro com a\(r\) coordenada -. Por exemplo, para traçar o ponto\(\left(2,\dfrac{\pi}{4}\right)\), moveríamos\(\dfrac{\pi}{4}\) as unidades no sentido anti-horário e, em seguida, a um comprimento\(2\) de um poste. Este ponto é plotado na grade na Figura\(\PageIndex{2}\).
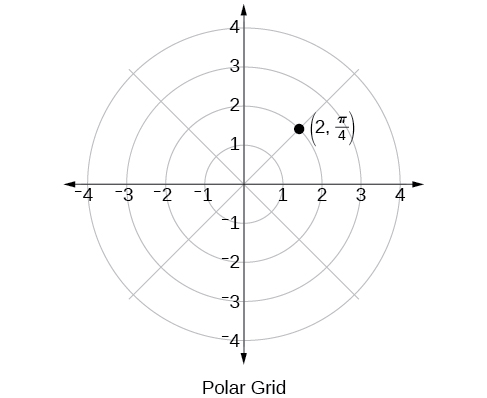
Figura\(\PageIndex{2}\)
Faça um gráfico do ponto\(\left(3,\dfrac{\pi}{2}\right)\) na grade polar.
Solução
O ângulo\(\dfrac{\pi}{2}\) é encontrado varrendo no sentido anti-horário a\(90°\) partir do eixo polar. O ponto está localizado a um comprimento de\(3\) unidades do pólo na\(\dfrac{\pi}{2}\) direção, conforme mostrado na Figura\(\PageIndex{3}\).
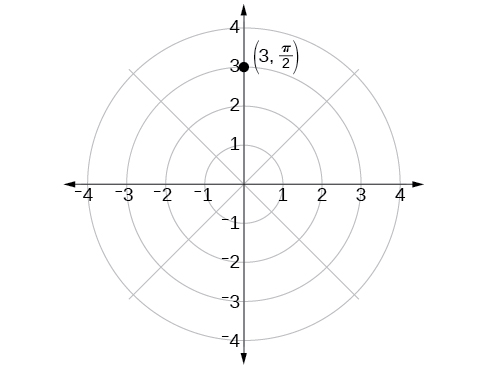
Figura\(\PageIndex{3}\)
Faça um gráfico do ponto\(\left(2, \dfrac{\pi}{3}\right)\) na grade polar.
- Responda
-
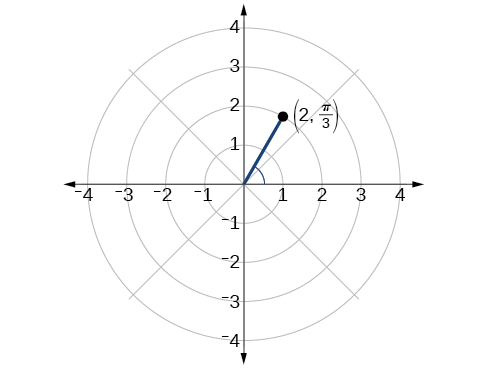
Figura\(\PageIndex{4}\)
Faça um gráfico do ponto\(\left(−2, \dfrac{\pi}{6}\right)\) na grade polar.
Solução
Sabemos que\(\dfrac{\pi}{6}\) está localizado no primeiro quadrante. No entanto,\(r=−2\). Podemos abordar a plotagem de um ponto com um negativo\(r\) de duas maneiras:
- Faça um gráfico do ponto\(\left(2,\dfrac{\pi}{6}\right)\) movendo-se\(\dfrac{\pi}{6}\) no sentido anti-horário e estendendo as\(2\) unidades de um segmento de linha direcionado até o primeiro quadrante. Em seguida, refaça o segmento da linha direcionada de volta através do pólo e continue\(2\) as unidades até o terceiro quadrante;
- Mova-se\(\dfrac{\pi}{6}\) no sentido anti-horário e desenhe o segmento de linha direcionado das\(2\) unidades do polo na direção negativa até o terceiro quadrante.
Veja a Figura\(\PageIndex{5a}\). Compare isso com o gráfico da coordenada polar\((2,π6)\) mostrado na Figura\(\PageIndex{5b}\).
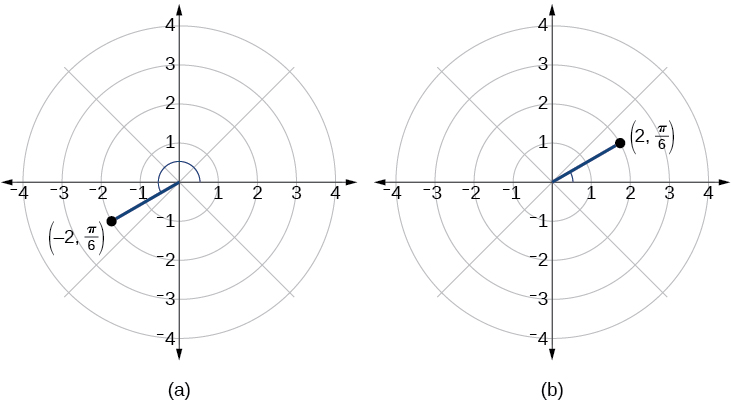
Figura\(\PageIndex{5}\)
Faça um gráfico dos pontos\(\left(3,−\dfrac{\pi}{6}\right)\) e\(\left(2,\dfrac{9\pi}{4}\right)\) na mesma grade polar.
- Responda
-
.jpg)
Figura\(\PageIndex{6}\)
Conversão de coordenadas polares em coordenadas retangulares
Quando recebemos um conjunto de coordenadas polares, talvez precisemos convertê-las em coordenadas retangulares. Para fazer isso, podemos relembrar as relações que existem entre as variáveis\(x\)\(y\)\(r\),,\(\theta\) e.
\(\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\)
\(\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\)
Soltar uma perpendicular do ponto no plano até o eixo x forma um triângulo reto, conforme ilustrado na Figura\(\PageIndex{7}\). Uma maneira fácil de lembrar as equações acima é pensar\(\cos \theta\) como o lado adjacente sobre a hipotenusa e\(\sin \theta\) como o lado oposto sobre a hipotenusa.
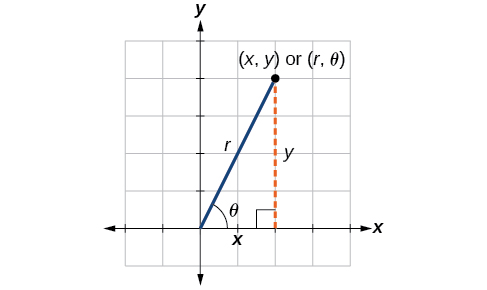
Figura\(\PageIndex{7}\)
Para converter coordenadas polares\((r, \theta)\) em coordenadas retangulares\((x, y)\), deixe
\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]
\[\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\]
- Dada a coordenada polar\((r,\theta)\), escreva\(x=r \cos \theta\)\(y=r \sin \theta\) e.
- Avalie\(\cos \theta\)\(\sin \theta\) e.
- Multiplique\(\cos \theta\) por\(r\) para encontrar a coordenada\(x\) - da forma retangular.
- Multiplique\(\sin \theta\) por\(r\) para encontrar a coordenada\(y\) - da forma retangular.
Escreva as coordenadas polares\(\left(3,\dfrac{\pi}{2}\right)\) como coordenadas retangulares.
Solução
Use os relacionamentos equivalentes.
\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y&= 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]
As coordenadas retangulares são\((0,3)\). Veja a Figura\(\PageIndex{8}\).
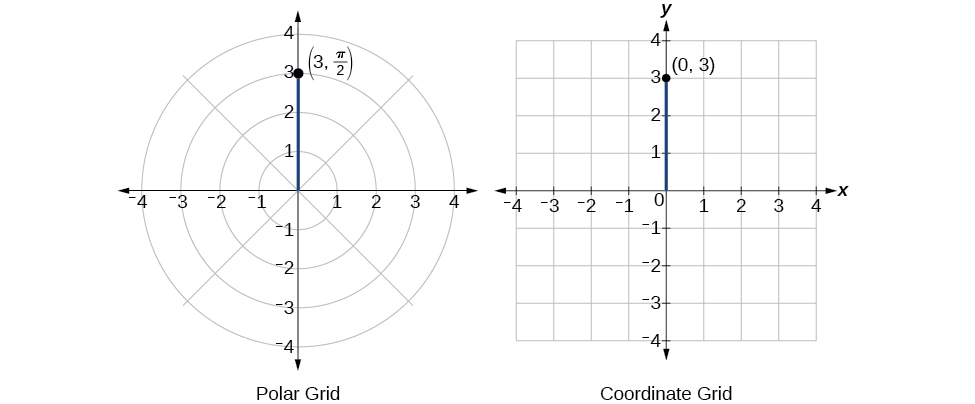
Figura\(\PageIndex{8}\)
Escreva as coordenadas polares\((−2,0)\) como coordenadas retangulares.
Solução
Veja a Figura\(\PageIndex{9}\). Escrevendo as coordenadas polares como retangulares, temos
\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]
As coordenadas retangulares também são\((−2,0)\).
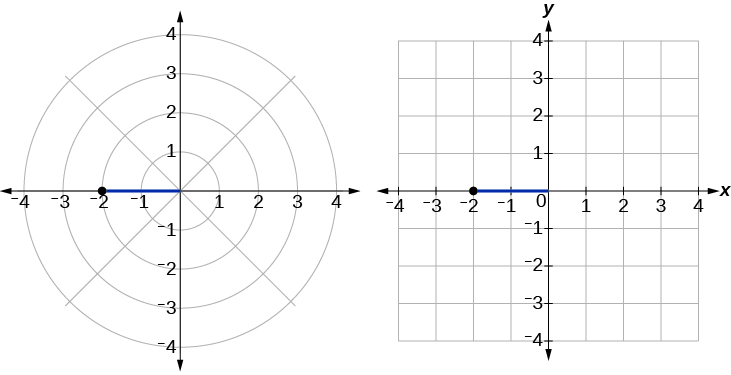
Figura\(\PageIndex{9}\)
Escreva as coordenadas polares\(\left(−1,\dfrac{2\pi}{3}\right)\) como coordenadas retangulares.
- Responda
-
\((x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\)
Conversão de coordenadas retangulares em coordenadas polares
Para converter coordenadas retangulares em coordenadas polares, usaremos duas outras relações familiares. Com essa conversão, no entanto, precisamos estar cientes de que um conjunto de coordenadas retangulares produzirá mais de um ponto polar.
A conversão de coordenadas retangulares em coordenadas polares requer o uso de uma ou mais das relações ilustradas na Figura\(\PageIndex{10}\).
\(\cos \theta=\dfrac{x}{r}\)ou\(x=r \cos \theta\)
\(\sin \theta=\dfrac{y}{r}\)ou\(y=r \sin \theta\)
\(r^2=x^2+y^2\)
\(\tan \theta=\dfrac{y}{x}\)
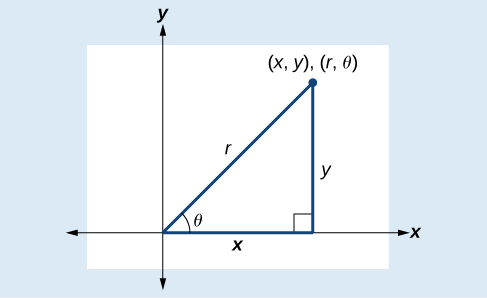
Figura\(\PageIndex{10}\)
Converta as coordenadas retangulares\((3,3)\) em coordenadas polares.
Solução
Vemos que o ponto original\((3,3)\) está no primeiro quadrante. Para encontrar\(\theta\), use a fórmula\(\tan \theta=\dfrac{y}{x}\). Isso dá
\[\begin{align*} \tan \theta&= \dfrac{3}{3}\\ \tan \theta&= 1\\ {\tan}^{-1}(1)&= \dfrac{\pi}{4} \end{align*}\]
Para encontrar\(r\), substituímos os valores por\(x\) e\(y\) na fórmula\(r=\sqrt{x^2+y^2}\). Sabemos que isso\(r\) deve ser positivo, como\(\dfrac{\pi}{4}\) no primeiro quadrante. Assim
\[\begin{align*} r&= \sqrt{3^2+3^2}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\]
Então,\(r=3\sqrt{2}\) e\(\theta=\dfrac{\pi}{4}\), nos dando o ponto polar\((3\sqrt{2},\dfrac{\pi}{4})\). Veja a Figura\(\PageIndex{11}\).
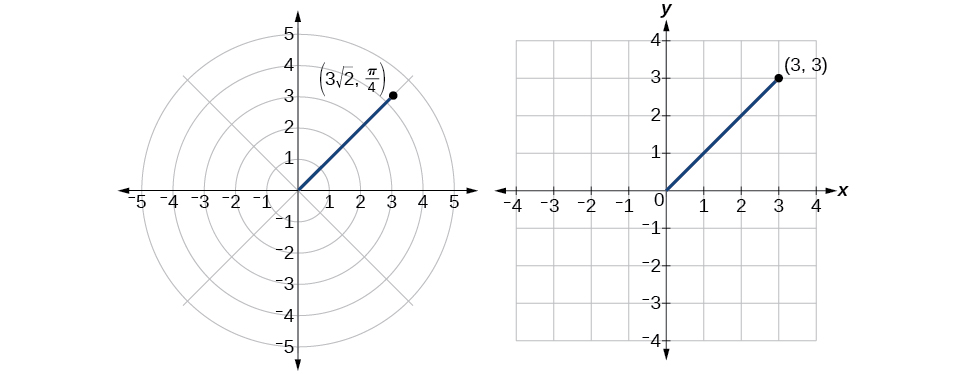
Figura\(\PageIndex{11}\)
Análise
Existem outros conjuntos de coordenadas polares que serão iguais à nossa primeira solução. Por exemplo, os pontos\(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) e\(\left(3\sqrt{2},−\dfrac{7\pi}{4}\right)\) coincidirão com a solução original do\(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). O ponto\(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) indica um movimento mais adiante no sentido anti-horário\(\pi\), o que é diretamente oposto\(\dfrac{\pi}{4}\). O raio é expresso como\(−3\sqrt{2}\). No entanto, o ângulo\(\dfrac{5\pi}{4}\) está localizado no terceiro quadrante e, como\(r\) é negativo, estendemos o segmento da linha direcionada na direção oposta, até o primeiro quadrante. Esse é o mesmo ponto de\(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). O ponto\(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) é um movimento mais adiante no sentido horário\(−\dfrac{7\pi}{4}\), de\(\dfrac{\pi}{4}\). O raio,\(3\sqrt{2}\), é o mesmo.
Transformando equações entre formas polares e retangulares
Agora podemos converter coordenadas entre a forma polar e retangular. A conversão de equações pode ser mais difícil, mas pode ser benéfico poder fazer a conversão entre as duas formas. Como há várias equações polares que não podem ser expressas claramente na forma cartesiana e vice-versa, podemos usar os mesmos procedimentos que usamos para converter pontos entre os sistemas de coordenadas. Podemos então usar uma calculadora gráfica para representar graficamente a forma retangular ou a forma polar da equação.
- Altere o MODE para POL, representando a forma polar.
- Pressione o botão Y= para abrir uma tela que permite a entrada de seis equações:\(r_1\),\(r_2\),...,\(r_6\).
- Insira a equação polar, defina igual\(r\) a.
- Pressione GRAPH.
Escreva a equação cartesiana\(x^2+y^2=9\) na forma polar.
Solução
O objetivo é eliminar\(x\) e\(y\) sair da equação\(r\) e introduzir\(\theta\) e. Idealmente, escreveríamos a equação\(r\) em função de\(\theta\). Para obter a forma polar, usaremos as relações entre\((x,y)\)\((r,\theta)\) e. Desde\(x=r \cos \theta\) e\(y=r \sin \theta\), podemos substituir e resolver\(r\).
\(\begin{align*} {(r \cos \theta)}^2+{(r \sin \theta)}^2&= 9\\ r^2 {\cos}^2 \theta+r^2 {\sin}^2 \theta&= 9\\ r^2({\cos}^2 \theta+{\sin}^2 \theta)&= 9\\ r^2(1)&= 9\qquad \text {Substitute } {\cos}^2 \theta+{\sin}^2 \theta=1\\ r&= \pm 3\qquad \text {Use the square root property.} \end{align*}\)
Assim,\(x^2+y^2=9\),\(r=3\), e\(r=−3\) deve gerar o mesmo gráfico. Veja a Figura\(\PageIndex{12}\).
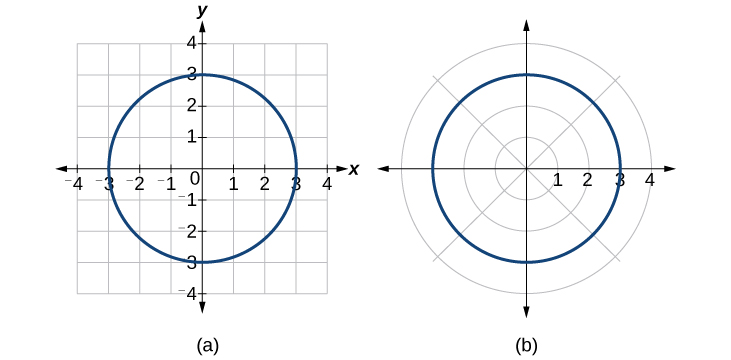
Figura\(\PageIndex{12}\): (a) Forma cartesiana\(x^2+y^2=9\) (b) Forma polar\(r=3\)
Para representar graficamente um círculo na forma retangular, precisamos primeiro resolver para\(y\).
\[\begin{align*} x^2+y^2&= 9\\ y^2&= 9-x^2\\ y&= \pm \sqrt{9-x^2} \end{align*}\]
Observe que essas são duas funções separadas, já que um círculo falha no teste da linha vertical. Portanto, precisamos inserir as raízes quadradas positivas e negativas na calculadora separadamente, como duas equações na forma\(Y_1=\sqrt{9−x^2}\)\(Y_2=−\sqrt{9−x^2}\) e. Pressione GRAPH.
Reescreva a equação cartesiana\(x^2+y^2=6y\) como uma equação polar.
Solução
Essa equação parece semelhante ao exemplo anterior, mas requer etapas diferentes para converter a equação.
Ainda podemos seguir os mesmos procedimentos que já aprendemos e fazer as seguintes substituições:
\(\begin{array}{ll} r^2=6y & \text{Use }x^2+y^2=r^2. \\ r^2=6r \sin \theta & \text{Substitute }y=r \sin \theta. \\ r^2−6r \sin \theta=0 & \text{Set equal to }0. \\ r(r−6 \sin \theta)=0 & \text{Factor and solve.} \\ r=0 & \text{We reject }r=0 \text{, as it only represents one point, }(0,0). \\ \text{or }r=6 \sin \theta \end{array}\)
Portanto, as equações\(x^2+y^2=6y\)\(r=6 \sin \theta\) devem nos dar o mesmo gráfico. Veja a Figura\(\PageIndex{13}\).
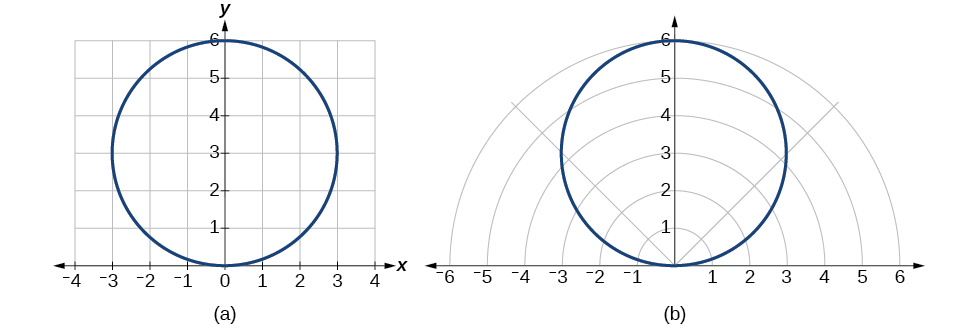
Figura\(\PageIndex{13}\): (a) Forma cartesiana\(x^2+y^2=6y\) (b) forma polar\(r=6 \sin \theta\)
A equação cartesiana ou retangular é plotada na grade retangular e a equação polar é plotada na grade polar. Claramente, os gráficos são idênticos.
Reescrevendo uma equação cartesiana na forma polar
Reescreva a equação cartesiana\(y=3x+2\) como uma equação polar.
- Responda
-
Usaremos os relacionamentos\(x=r \cos \theta\)\(y=r \sin \theta\) e.
\(\begin{array}{cl} y=3x+2 \\ r \sin \theta=3r \cos \theta+2 \\ r \sin \theta−3r \cos \theta=2 \\ r(\sin \theta−3 \cos \theta)=2 & \text{Isolate }r. \\ r=2 \sin \theta−3\cos \theta & \text{Solve for }r. \end{array}\)
Reescreva a equação cartesiana\(y^2=3−x^2\) na forma polar.
- Responda
-
\(r=\sqrt{3}\)
Identifique e represente graficamente equações polares convertendo em equações retangulares
Aprendemos como converter coordenadas retangulares em coordenadas polares e vimos que os pontos são realmente os mesmos. Também transformamos equações polares em equações retangulares e vice-versa. Agora vamos demonstrar que seus gráficos, embora desenhados em grades diferentes, são idênticos.
Converta a equação\(r=2 \sec \theta\) polar em uma equação retangular e desenhe seu gráfico correspondente.
Solução
A conversão é
\[\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \theta &=2 \\ x &=2 \end{align*}\]
Observe que a equação\(r=2 \sec \theta\) desenhada na grade polar é claramente a mesma que a linha vertical\(x=2\) desenhada na grade retangular (veja a Figura\(\PageIndex{14}\)). Assim como\(x=c\) a forma padrão para uma linha vertical na forma retangular,\(r=c \sec \theta\) é a forma padrão para uma linha vertical na forma polar.
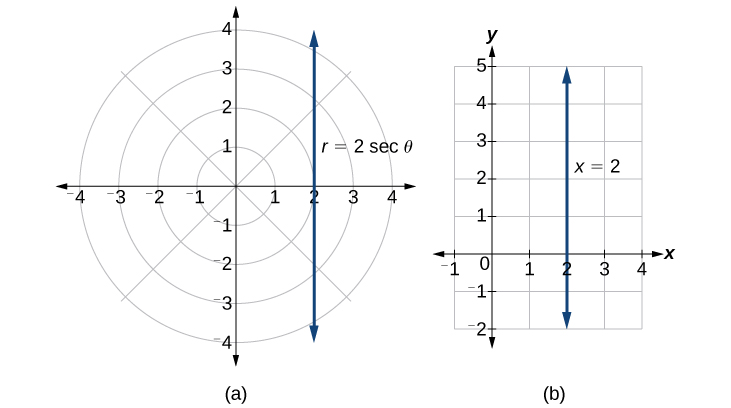
Figura\(\PageIndex{14}\): (a) Grade polar (b) Sistema de coordenadas retangulares
Uma discussão semelhante demonstraria que o gráfico da função\(r=2 \csc \theta\) será a linha horizontal\(y=2\). Na verdade,\(r=c \csc \theta\) é a forma padrão para uma linha horizontal na forma polar, correspondente à forma retangular\(y=c\).
Reescreva a equação polar\(r=\dfrac{3}{1−2 \cos \theta}\) como uma equação cartesiana.
Solução
O objetivo é eliminar\(\theta\) e\(r\),\(x\) e introduzir\(y\) e. Limpamos a fração e, em seguida, usamos a substituição. Para\(r\) substituir por\(x\) e\(y\), devemos usar a expressão\(x^2+y^2=r^2\).
\(\begin{array} r =\dfrac{3}{1−2 \cos \theta} \\ r(1−2 \cos \theta)=3 \\ r\left(1−2\left(\dfrac{x}{r}\right)\right)=3 & \text{Use }\cos \theta=\dfrac{x}{r} \text{ to eliminate }\theta. \\ r−2x=3 \\ r=3+2x & \text{Isolate }r. \\ r^2={(3+2x)}^2 & \text{Square both sides.} \\ x^2+y^2={(3+2x)}^2 & \text{Use }x^2+y^2=r^2. \end{array}\)
A equação cartesiana é\(x^2+y^2={(3+2x)}^2\). No entanto, para representá-lo graficamente, especialmente usando uma calculadora gráfica ou um programa de computador, queremos isolá-lo\(y\).
\[\begin{align*} x^2+y^2 &= {(3+2x)}^2 \\ y^2 &= {(3+2x)}^2-x^2 \\ y &= \pm {(3+2x)}^2-x^2 \end{align*}\]
Quando toda a nossa equação for alterada de\(r\) e\(\theta\) para\(x\) e\(y\), podemos parar, a menos que seja solicitado a resolver\(y\) ou simplificar. Veja a Figura\(\PageIndex{15}\).
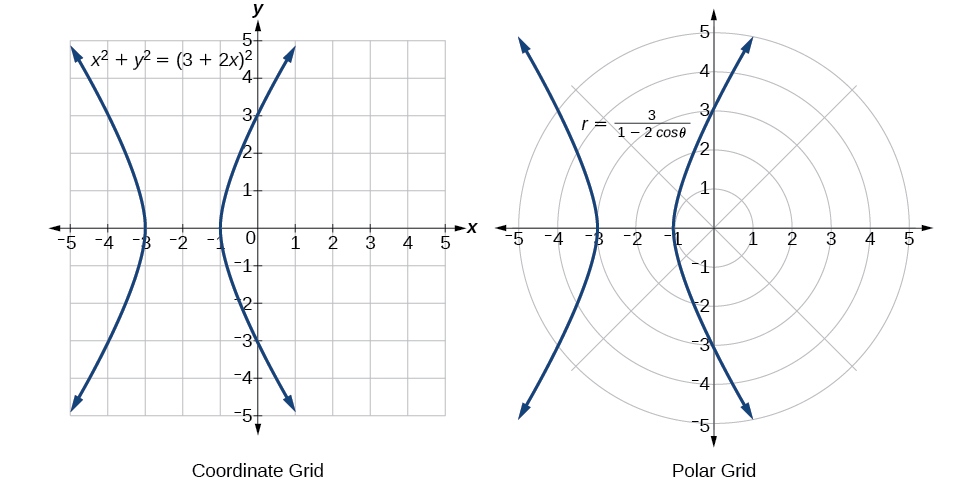
Figura\(\PageIndex{15}\)
A forma de “ampulheta” do gráfico é chamada de hipérbole. As hipérboles têm muitas características e aplicações geométricas interessantes, que investigaremos mais detalhadamente em Geometria Analítica.
Análise
Neste exemplo, o lado direito da equação pode ser expandido e a equação ainda mais simplificada, conforme mostrado acima. No entanto, a equação não pode ser escrita como uma única função na forma cartesiana. Talvez queiramos escrever a equação retangular na forma padrão da hipérbole. Para fazer isso, podemos começar com a equação inicial.
\(\begin{array}{ll} x^2+y^2={(3+2x)}^2 \\ x^2+y^2−{(3+2x)}^2=0 \\ x^2+y^2−(9+12x+4x^2)=0 \\ x^2+y^2−9−12x−4x^2=0 \\ −3x^2−12x+y^2=9 & \text{Multiply through by }−1. \\ 3x^2+12x−y^2=−9 \\ 3(x^2+4x)−y2=−9 & \text{Organize terms to complete the square for }x. \\ 3(x^2+4x+4)−y^2=−9+12 \\ 3{(x+2)}^2−y^2=3 \\ {(x+2)}^2−\dfrac{y^2}{3}=1\end{array}\)
Reescreva a equação polar\(r=2 \sin \theta\) na forma cartesiana.
- Responda
-
\(x^2+y^2=2y\)ou, na forma padrão para um círculo,\(x^2+{(y−1)}^2=1\)
Reescreva a equação polar\(r=\sin(2\theta)\) na forma cartesiana.
Solução
\(\begin{array}{cl} r=\sin(2\theta) & \text{Use the double angle identity for sine.} \\ r=2 \sin \theta \cos \theta & \text{Use }\cos \theta=\dfrac{x}{r} \text{ and } \sin \theta=\dfrac{y}{r}. \\ r=2 \dfrac{x}{r})(\dfrac{y}{r}) & \text{ Simplify.} \\ r=\dfrac{2xy}{r^2} & \text{Multiply both sides by }r^2. \\ r^3=2xy \\ {(x^2+y^2)}^3=2xy & \text{As }x^2+y^2=r^2, r=\sqrt{x^2+y^2}. \end{array}\)
Essa equação também pode ser escrita como
\({(x^2+y^2)}^{\frac{3}{2}}=2xy \text{ or }x^2+y^2={(2xy)}^{\frac{2}{3}}\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com coordenadas polares.
Equações-chave
| Fórmulas de conversão |
\(\cos \theta=\dfrac{x}{r} \rightarrow x=r \cos\theta\) \(\sin \theta=\dfrac{y}{r} \rightarrow y=r \sin \theta\) \(r^2=x^2+y^2\) \(\tan \theta=\dfrac{y}{x}\) |
Conceitos-chave
- A grade polar é representada como uma série de círculos concêntricos que se irradiam do polo ou origem.
- Para traçar um ponto na forma\((r,\theta)\),\(\theta>0\), mova-se no sentido anti-horário a partir do eixo polar em um ângulo de e\(\theta\), em seguida, estenda um segmento de linha direcionado do pólo no comprimento de\(r\) na direção de\(\theta\). Se\(\theta\) for negativo, mova-se no sentido horário e estenda um segmento de linha direcionado no comprimento de\(r\) na direção de\(\theta\). Veja o exemplo\(\PageIndex{1}\).
- Se\(r\) for negativo, estenda o segmento da linha direcionada na direção oposta de\(\theta\). Veja o exemplo\(\PageIndex{2}\).
- Para converter de coordenadas polares em coordenadas retangulares, use as fórmulas\(x=r \cos \theta\)\(y=r \sin \theta\) e. Veja o exemplo\(\PageIndex{3}\) e o exemplo\(\PageIndex{4}\).
- Para converter de coordenadas retangulares em coordenadas polares, use uma ou mais das fórmulas:\(\cos \theta=\dfrac{x}{r}\)\(\sin \theta=\dfrac{y}{r}\)\(\tan \theta=\dfrac{y}{x}\),,\(r=\sqrt{x^2+y^2}\) e. Veja o exemplo\(\PageIndex{5}\).
- Transformar equações entre formas polares e retangulares significa fazer as substituições apropriadas com base nas fórmulas disponíveis, junto com manipulações algébricas. Veja exemplo\(\PageIndex{6}\)\(\PageIndex{7}\), exemplo e exemplo\(\PageIndex{8}\).
- O uso das substituições apropriadas torna possível reescrever uma equação polar como uma equação retangular e, em seguida, representá-la graficamente no plano retangular. Veja exemplo\(\PageIndex{9}\)\(\PageIndex{10}\), exemplo e exemplo\(\PageIndex{11}\).


