8.2: Triângulos não retos - Lei dos cossenos
- Page ID
- 189161
Nesta seção, você irá:
- Use a Lei dos Cossenos para resolver triângulos oblíquos.
- Resolva problemas aplicados usando a Lei dos Cossenos.
- Use a fórmula de Heron para encontrar a área de um triângulo.
Suponha que um barco saia do porto, viaje\(10\) milhas, gire\(20\) graus e viaje mais 8 milhas, conforme mostrado na Figura A que\(\PageIndex{1}\) distância do porto está o barco?
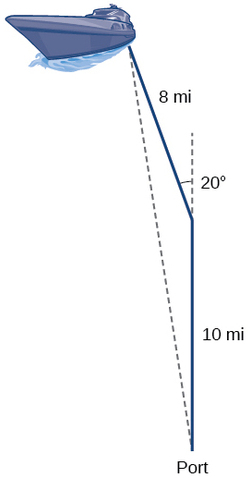
Figura\(\PageIndex{1}\)
Infelizmente, embora a Lei de Sines nos permita abordar muitos casos de triângulos não retos, ela não nos ajuda com triângulos em que o ângulo conhecido está entre dois lados conhecidos, um triângulo SAS (lado lateral) ou quando todos os três lados são conhecidos, mas nenhum ângulo é conhecido, um triângulo SSS (lado lateral lateral). Nesta seção, investigaremos outra ferramenta para resolver triângulos oblíquos descrita por esses dois últimos casos.
Usando a Lei dos Cossenos para Resolver Triângulos Oblíquos
A ferramenta que precisamos para resolver o problema da distância do barco do porto é a Lei dos Cossenos, que define a relação entre medidas de ângulo e comprimentos laterais em triângulos oblíquos. Três fórmulas compõem a Lei dos Cossenos. À primeira vista, as fórmulas podem parecer complicadas porque incluem muitas variáveis. No entanto, uma vez que o padrão é compreendido, é mais fácil trabalhar com a Lei dos Cossenos do que a maioria das fórmulas nesse nível matemático.
Entender como a Lei dos Cossenos é derivada será útil no uso das fórmulas. A derivação começa com o Teorema de Pitágoras Generalizado, que é uma extensão do Teorema de Pitágoras para triângulos não retos. Funciona assim: Um triângulo arbitrário não reto\(ABC\) é colocado no plano coordenado com vértice\(A\) na origem, lado\(c\) desenhado ao longo do eixo x e vértice\(C\) localizado\((x,y)\) em algum ponto do plano, conforme ilustrado na Figura\(\PageIndex{2}\). Geralmente, os triângulos existem em qualquer parte do plano, mas, para essa explicação, colocaremos o triângulo conforme indicado.
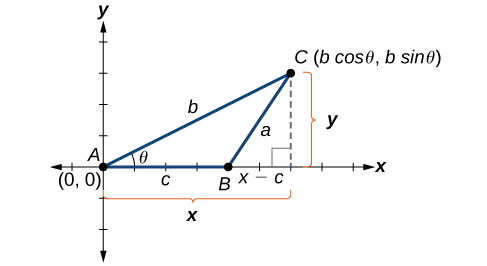
Figura\(\PageIndex{2}\)
Podemos soltar uma perpendicular de\(C\) até o eixo x (essa é a altitude ou altura). Relembrando as identidades trigonométricas básicas, sabemos que
\(\cos \theta=\dfrac{x(adjacent)}{b(hypotenuse)}\)e\(\sin \theta=\dfrac{y(opposite)}{b(hypotenuse)}\)
Em termos de\(\theta\),\(x=b \cos \theta\)\(y=b \sin \theta\) e. O\((x,y)\) ponto localizado em\(C\) tem coordenadas\((b \cos \theta, b \sin \theta)\). Usando o lado\((x−c)\) como uma perna de um triângulo reto e\(y\) como a segunda perna, podemos encontrar o comprimento da hipotenusa\(a\) usando o Teorema de Pitágoras. Assim,
\ (\ begin {array} {ll} a^2= {(x−c)} ^2+y^2\\ [4pt]\;\;\;\;\; = {(b\ cos\ theta−c)} ^2+ {(b\ sin\ theta)} ^2 &\ texto {Substituto} (b\ cos\ theta)\ texto {para} x\ texto {e} (b\ sin\ theta)\ text {para} y\\ [4pt]\;\;\;\;\;\; = (b^2 {\ cos} ^2\ theta−2bc\ cos\ theta+c^2) +b^2 {\ sin} ^2\ theta &\ text {Expandir o perfeito quadrado.}\\ [4pt]\;\;\;\; =b^2 {\ cos} ^2\ theta+b^2 {\ sin} ^2\ theta+c^2−2bc\ cos\ theta &\ text {Termos do grupo observando que} {\ cos} ^2\ theta+ {\ sin} ^2\ theta=1\\ [4pt];\;\;\;\; =b^2 ({\ cos} ^2\ theta+ {\ sin} ^2\ theta) +c^2−2bc\ cos\ theta &\ text {Fator out} b^2\\ [4pt]
a^2=b^2+c^2−2bc\ cos\ theta \ end {matriz}\)
A fórmula derivada é uma das três equações da Lei dos Cossenos. As outras equações são encontradas de forma semelhante.
Lembre-se de que é sempre útil esboçar o triângulo ao resolver ângulos ou lados. Em um cenário real, tente desenhar um diagrama da situação. À medida que surgirem mais informações, o diagrama pode ter que ser alterado. Faça essas alterações no diagrama e, no final, o problema será mais fácil de resolver.
A Lei dos Cossenos afirma que o quadrado de qualquer lado de um triângulo é igual à soma dos quadrados dos outros dois lados menos o dobro do produto dos outros dois lados e o cosseno do ângulo incluído.
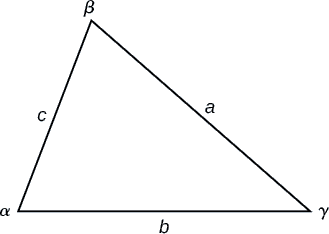
Figura\(\PageIndex{3}\)
Para triângulos rotulados como na Figura\(\PageIndex{3}\), com ângulos\(\alpha\)\(\beta\) e\(\gamma\) lados opostos correspondentes\(a\), e\(b\), respectivamente\(c\), a Lei dos Cossenos é dada como três equações.
\[a^2=b^2+c^2−2bc \cos \alpha\]
\[b^2=a^2+c^2−2ac \cos \beta\]
\[c^2=a^2+b^2−2ab \cos \gamma\]
Para resolver uma medição lateral ausente, a medida do ângulo oposto correspondente é necessária.
Ao resolver um ângulo, a medida correspondente do lado oposto é necessária. Podemos usar outra versão da Lei dos Cossenos para resolver um ângulo.
\[\cos \alpha=\dfrac{b^2+c^2−a^2}{2bc}\]
\[\cos \beta=\dfrac{a^2+c^2−b^2}{2ac}\]
\[\cos \gamma=\dfrac{a^2+b^2−c^2}{2ab}\]
- Desenhe o triângulo. Identifique as medidas dos lados e ângulos conhecidos. Use variáveis para representar as medidas dos lados e ângulos desconhecidos.
- Aplique a Lei dos Cossenos para encontrar o comprimento do lado ou ângulo desconhecido.
- Aplique a Lei dos Sines ou Cossenos para encontrar a medida de um segundo ângulo.
- Calcule a medida do ângulo restante.
Encontre o lado e os ângulos desconhecidos do triângulo na Figura\(\PageIndex{4}\).
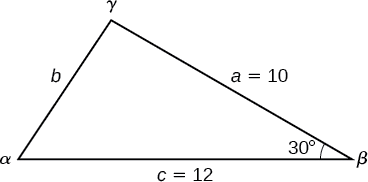
Figura\(\PageIndex{4}\)
Solução
Primeiro, anote o que é dado: dois lados e o ângulo entre eles. Esse arranjo é classificado como SAS e fornece os dados necessários para aplicar a Lei dos Cossenos.
Cada uma das três leis dos cossenos começa com o quadrado de um lado desconhecido oposto a um ângulo conhecido. Neste exemplo, o primeiro lado a ser resolvido é o lado\(b\), pois sabemos a medição do ângulo oposto\(\beta\).
\(\begin{array}{ll} b^2=a^2+c^2−2ac \cos \beta \\[4pt] b^2={10}^2+{12}^2−2(10)(12)\cos(30°) & \text{Substitute the measurements for the known quantities.} \\[4pt] b^2=100+144−240 \left(\dfrac{\sqrt{3}}{2}\right) & \text{Evaluate the cosine and begin to simplify.} \\[4pt] b^2=244−120\sqrt{3} \\[4pt] b=\sqrt{244−120\sqrt{3}} & \text{Use the square root property.} \\[4pt] b≈6.013 \end{array}\)
Como estamos resolvendo um comprimento, usamos apenas a raiz quadrada positiva. Agora que sabemos o comprimento\(b\), podemos usar a Lei de Sines para preencher os ângulos restantes do triângulo. Resolvendo o ângulo\(\alpha\), temos
\(\begin{array}{cc} \dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b} \\[4pt] \dfrac{\sin \alpha}{10}=\dfrac{\sin(30°)}{6.013} \\[4pt] \sin \alpha=\dfrac{10\sin(30°)}{6.013} & \text{Multiply both sides of the equation by }10. \\[4pt] \alpha={\sin}^{−1}\left(\dfrac{10\sin(30°)}{6.013}\right) & \text{Find the inverse sine of } \dfrac{10\sin(30°)}{6.013}. \\[4pt] \alpha≈56.3° \end{array}\)
A outra possibilidade\(\alpha\) seria\(\alpha=180°-56.3°≈123.7°\). No diagrama original,\(\alpha\) é adjacente ao lado mais longo, então\(\alpha\) é um ângulo agudo e, portanto, não\(123.7°\) faz sentido. Observe que, se optarmos por aplicar a Lei dos Cossenos, chegaremos a uma resposta única. Não precisamos considerar as outras possibilidades, pois o cosseno é único para ângulos entre\(0°\)\(180°\) e. Prosseguindo\(\alpha≈56.3°\), podemos então encontrar o terceiro ângulo do triângulo.
\[\begin{align*} \gamma&= 180^{\circ}-30^{\circ}-56.3^{\circ}\\ &\approx 93.7^{\circ} \end{align*}\]
O conjunto completo de ângulos e lados é
\(\alpha≈56.3°\)\(a=10\)
\(\beta=30°\)\(b≈6.013\)
\(\gamma≈93.7°\)\(c=12\)
Encontre o lado e os ângulos ausentes do triângulo fornecido:\(\alpha=30°\),\(b=12\),\(c=24\).
- Resposta
-
\(a≈14.9\),\(\beta≈23.8°\),\(\gamma≈126.2°\).
Encontre o ângulo\(\alpha\) para o triângulo dado se for lado\(a=20\)\(b=25\), lado e lado\(c=18\).
Solução
Neste exemplo, não temos ângulos. Podemos resolver qualquer ângulo usando a Lei dos Cossenos. Para resolver o ângulo\(\alpha\), temos
\(\begin{array}{ll} a^2=b^2+c^2−2bc \cos \alpha \\[4pt] {20}^2={25}^2+{18}^2−2(25)(18)\cos \alpha & \text{Substitute the appropriate measurements.} \\[4pt] 400=625+324−900 \cos \alpha & \text{ Simplify in each step.} \\[4pt] 400=949−900 \cos \alpha \\[4pt] −549=−900 \cos \alpha & \text{Isolate }\cos \alpha. \\[4pt] 0.61≈\cos \alpha & \text{Find the inverse cosine.} \\[4pt] \alpha≈52.4° \end{array}\)
Veja a Figura\(\PageIndex{5}\).
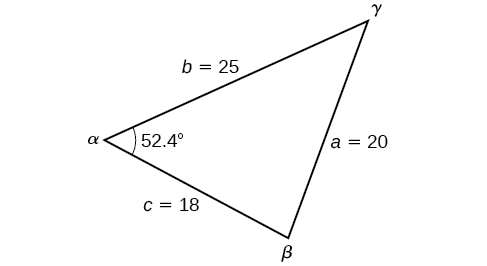
Figura\(\PageIndex{5}\)
Análise
Como o cosseno inverso pode retornar qualquer ângulo entre\(0\) e\(180\) graus, não haverá nenhum caso ambíguo usando esse método.
Dado\(a=5\),\(b=7\), e\(c=10\), encontre os ângulos que faltam.
- Resposta
-
\(\alpha≈27.7°\),\(\beta≈40.5°\),\(\gamma≈111.8°\)
Resolvendo problemas aplicados usando a Lei dos Cossenos
Assim como a Lei de Sines forneceu as equações apropriadas para resolver uma série de aplicações, a Lei dos Cossenos é aplicável às situações em que os dados fornecidos se encaixam nos modelos dos cossenos. Podemos vê-los nos campos de navegação, levantamento, astronomia e geometria, só para citar alguns.
Em muitos telefones celulares com GPS, uma localização aproximada pode ser fornecida antes que o sinal GPS seja recebido. Isso é feito por meio de um processo chamado triangulação, que funciona usando as distâncias de dois pontos conhecidos. Suponha que haja duas torres de telefonia celular ao alcance de um telefone celular. As duas torres estão localizadas a\(6000\) pés de distância ao longo de uma rodovia reta, indo de leste a oeste, e o telefone celular fica ao norte da rodovia. Com base no atraso do sinal, pode-se determinar que o sinal está a\(5050\) pés da primeira torre e a\(2420\) pés da segunda torre. Determine a posição do celular ao norte e leste da primeira torre e determine a que distância ele está da rodovia.
Solução
Para simplificar, começamos desenhando um diagrama semelhante à Figura\(\PageIndex{6}\) e rotulando nossas informações fornecidas.
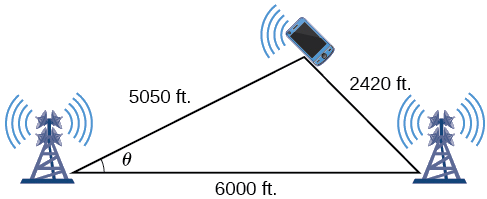
Figura\(\PageIndex{6}\)
Usando a Lei dos Cossenos, podemos resolver o ângulo\(\theta\). Lembre-se de que a Lei dos Cossenos usa o quadrado de um lado para encontrar o cosseno do ângulo oposto. Para este exemplo\(a=2420\), deixe\(b=5050\),\(c=6000\) e. Assim,\(\theta\) corresponde ao lado oposto\(a=2420\).
\[\begin{align*} a^2 & =b^2+c^2−2bc \cos \theta \\[4pt] {(2420)}^2 &={(5050)}^2+{(6000)}^2−2(5050)(6000) \cos \theta \\[4pt] \cos \theta &≈ 0.9183 \\[4pt] \theta &≈ {\cos}^{−1}(0.9183) \\[4pt] \theta &≈ 23.3° \end{align*}\]
Para responder às perguntas sobre a posição do telefone ao norte e leste da torre e a distância até a rodovia, solte uma perpendicular da posição do telefone celular, como na Figura\(\PageIndex{7}\). Isso forma dois triângulos retos, embora precisemos apenas do triângulo reto que inclui a primeira torre para esse problema.
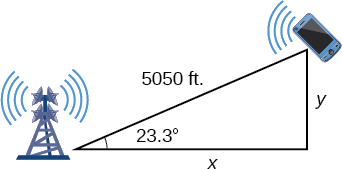
Figura\(\PageIndex{7}\)
Usando o ângulo\(\theta=23.3\)° e as identidades trigonométricas básicas, podemos encontrar as soluções. Assim
\[\begin{align*} \cos(23.3°) &= \dfrac{x}{5050} \\[4pt] x &= 5050\cos(23.3°) \\[4pt] x &≈ 4638.15\, feet\\[4pt] \sin(23.3°) &= \dfrac{y}{5050} \\[4pt] y &= 5050\sin(23.3°) \\[4pt] y &≈1997.5 \, feet \end{align*}\]
O telefone celular fica a aproximadamente\(4638\) pés a leste e\(1998\) pés ao norte da primeira torre, e\(1998\) pés da rodovia.
Voltando ao nosso problema no início desta seção, suponha que um barco saia do porto, viaje\(10\) milhas,\(20\) gire graus e viaje outros\(8\) quilômetros. A que distância do porto está o barco? O diagrama é repetido aqui na Figura\(\PageIndex{8}\).
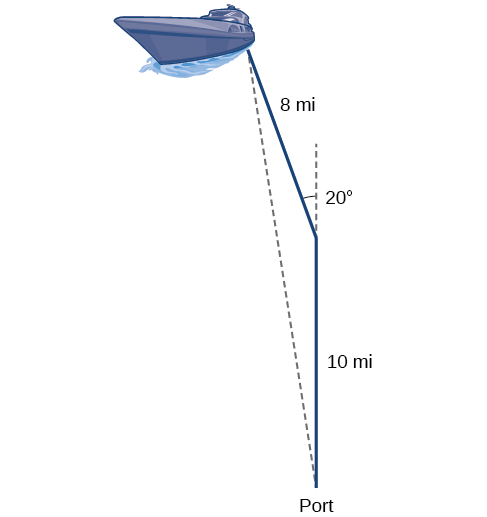
Figura\(\PageIndex{8}\)
Solução
O barco girou 20 graus, então o ângulo obtuso do triângulo não reto é o ângulo suplementar,\(180°−20°=160°\). Com isso, podemos utilizar a Lei dos Cossenos para encontrar o lado ausente do triângulo obtuso — a distância do barco até o porto.
\[\begin{align*} x^2 &= 8^2+{10}^2−2(8)(10)\cos(160°) \\[4pt] x^2 &= 314.35 \\[4pt] x &= \sqrt{314.35} \\[4pt] x&≈17.7\, miles \end{align*}\]
O barco está a cerca de\(17.7\) milhas do porto.
Usando a fórmula de Heron para encontrar a área de um triângulo
Já aprendemos como encontrar a área de um triângulo oblíquo quando conhecemos dois lados e um ângulo. Também conhecemos a fórmula para encontrar a área de um triângulo usando a base e a altura. Quando conhecemos os três lados, no entanto, podemos usar a fórmula de Heron em vez de encontrar a altura. Garça de Alexandria foi um geômetro que viveu durante o primeiro século d.C. Ele descobriu uma fórmula para encontrar a área dos triângulos oblíquos quando três lados são conhecidos.
A fórmula de Heron encontra a área dos triângulos oblíquos nos quais os lados\(a\)\(b\),, e\(c\) são conhecidos.
\[Area=\sqrt{s(s−a)(s−b)(s−c)}\]
onde\(s=\dfrac{(a+b+c)}{2}\) está a metade do perímetro do triângulo, às vezes chamado de semiperímetro.
Encontre a área do triângulo na Figura\(\PageIndex{9}\) usando a fórmula de Heron.
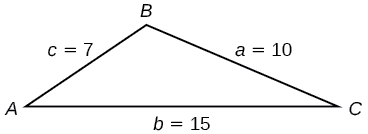
Figura\(\PageIndex{9}\)
Solução
Primeiro, calculamos\(s\).
\[\begin{align*} s&= \dfrac{(a+b+c)}{2}\\ s&= \dfrac{(10+15+7)}{2}\\ &= 16 \end{align*}\]
Em seguida, aplicamos a fórmula.
\[\begin{align*} Area&= \sqrt{s(s-a)(s-b)(s-c)}\\ Area&= \sqrt{16(16-10)(16-15)(16-7)}\\ Area&\approx 29.4 \end{align*}\]
A área é de aproximadamente unidades\(29.4\) quadradas.
Use a fórmula de Heron para encontrar a área de um triângulo com lados de comprimentos\(a=29.7\)\(b=42.3\) ft, ft e\(c=38.4\) ft.
- Resposta
-
Área = pés\(552\) quadrados
Um promotor da cidade de Chicago quer construir um prédio composto por lofts de artistas em um terreno triangular cercado pela Rush Street, Wabash Avenue e Pearson Street. A fachada ao longo da Rush Street é de aproximadamente\(62.4\) metros, ao longo da Wabash Avenue é de aproximadamente\(43.5\) metros, e ao longo da Pearson Street é de aproximadamente\(34.1\) metros. Quantos metros quadrados estão disponíveis para o desenvolvedor? Veja a Figura\(\PageIndex{10}\) para uma visão da propriedade da cidade.
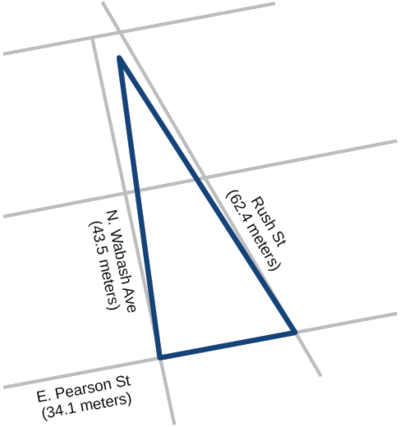
Figura\(\PageIndex{10}\)
Solução
Encontre a medida para\(s\), que é metade do perímetro.
\[\begin{align*} s&= \dfrac{(62.4+43.5+34.1)}{2}\\ s&= 70\; m\\ \text {Apply Heron's formula.}\\ Area&= \sqrt{70(70-62.4)(70-43.5)(70-34.1)}\\ Area&= \sqrt{506,118.2}\\ Area&\approx 711.4 \end{align*}\]
O desenvolvedor tem cerca de metros\(711.4\) quadrados.
Encontre a área de um triângulo dados\(a=4.38\) pés,\(b=3.79\) pés e\(c=5.22\) pés.
- Resposta
-
cerca de pés\(8.15\) quadrados
Acesse esses recursos on-line para obter instruções e práticas adicionais com a Lei dos Cossenos.
Equações chave
| Lei dos Cossenos |
\(a^2=b^2+c^2−2bc \cos \alpha\) \(b^2=a^2+c^2−2ac \cos \beta\) \(c^2=a^2+b^2−2ab \cos \gamma\) |
| Fórmula de Heron |
\(Area=\sqrt{s(s−a)(s−b)(s−c)}\) onde\(s=\dfrac{(a+b+c)}{2}\) |
Conceitos chave
- A Lei dos Cossenos define a relação entre as medidas dos ângulos e os comprimentos dos lados em triângulos oblíquos.
- O Teorema de Pitágoras Generalizado é a Lei dos Cossenos para dois casos de triângulos oblíquos: SAS e SSS. Soltar uma perpendicular imaginária divide o triângulo oblíquo em dois triângulos retos ou forma um triângulo reto, o que permite que os lados sejam relacionados e as medidas sejam calculadas. Veja o exemplo\(\PageIndex{1}\) e o exemplo\(\PageIndex{2}\).
- A Lei dos Cossenos é útil para muitos tipos de problemas aplicados. O primeiro passo para resolver esses problemas geralmente é desenhar um esboço do problema apresentado. Se as informações fornecidas se encaixarem em um dos três modelos (as três equações), aplique a Lei dos Cossenos para encontrar uma solução. Veja o exemplo\(\PageIndex{3}\) e o exemplo\(\PageIndex{4}\).
- A fórmula de Heron permite o cálculo da área em triângulos oblíquos. Todos os três lados devem ser conhecidos para aplicar a fórmula de Heron. Veja o exemplo\(\PageIndex{5}\) e veja o exemplo\(\PageIndex{6}\).


