8.1: Triângulos não retos - Lei de Sines
- Page ID
- 189126
- Use a Lei de Sines para resolver triângulos oblíquos.
- Encontre a área de um triângulo oblíquo usando a função seno.
- Resolva problemas aplicados usando a Lei de Sines.
Suponha que duas estações de radar localizadas\(20\) a milhas de distância detectem uma aeronave entre elas. O ângulo de elevação medido pela primeira estação é de\(35\) graus, enquanto o ângulo de elevação medido pela segunda estação é de\(15\) graus. Como podemos determinar a altitude da aeronave? Vemos na Figura\(\PageIndex{1}\) que o triângulo formado pela aeronave e pelas duas estações não é um triângulo reto, então não podemos usar o que sabemos sobre triângulos retos. Nesta seção, descobriremos como resolver problemas envolvendo triângulos não retos.
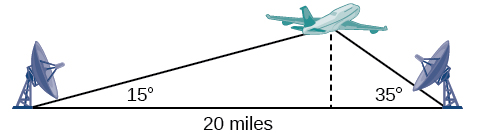
Figura\(\PageIndex{1}\)
Usando a Lei de Sines para resolver triângulos oblíquos
Em qualquer triângulo, podemos desenhar uma altitude, uma linha perpendicular de um vértice ao lado oposto, formando dois triângulos retos. Seria preferível, no entanto, ter métodos que pudéssemos aplicar diretamente a triângulos não retos sem primeiro ter que criar triângulos retos.
Qualquer triângulo que não seja um triângulo reto é um triângulo oblíquo. Resolver um triângulo oblíquo significa encontrar as medidas dos três ângulos e dos três lados. Para fazer isso, precisamos começar com pelo menos três desses valores, incluindo pelo menos um dos lados. Investigaremos três possíveis situações problemáticas do triângulo oblíquo:
ASA (ângulo lateral angular) Conhecemos as medidas de dois ângulos e do lado incluído. Veja a Figura\(\PageIndex{2}\).
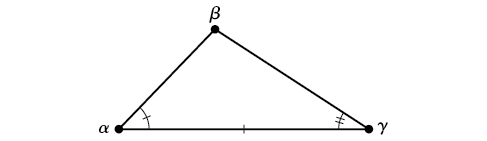
Figura\(\PageIndex{2}\)
AAS (angle-angle-side) Conhecemos as medidas de dois ângulos e de um lado que não está entre os ângulos conhecidos. Veja a Figura\(\PageIndex{3}\).
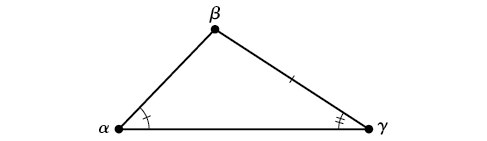
Figura\(\PageIndex{3}\)
SSA (ângulo lateral) Conhecemos as medidas de dois lados e um ângulo que não está entre os lados conhecidos. Veja a Figura\(\PageIndex{4}\).
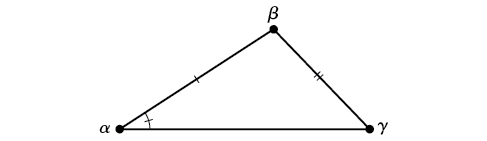
Figura\(\PageIndex{4}\)
Saber como abordar cada uma dessas situações nos permite resolver triângulos oblíquos sem precisar soltar uma perpendicular para formar dois triângulos retos. Em vez disso, podemos usar o fato de que a razão entre a medição de um dos ângulos e o comprimento do lado oposto será igual às outras duas razões da medida do ângulo em relação ao lado oposto. Vamos ver como essa afirmação é derivada considerando o triângulo mostrado na Figura\(\PageIndex{5}\).
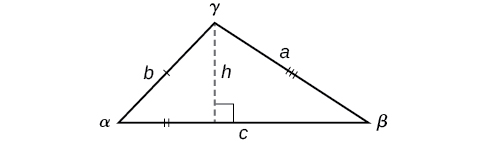
Figura\(\PageIndex{5}\)
Usando os relacionamentos do triângulo certo, nós sabemos que\(\sin \alpha=\dfrac{h}{b}\)\(\sin \beta=\dfrac{h}{a}\) e. Resolver as duas equações para\(h\) fornece duas expressões diferentes para\(h\).
\(h=b \sin \alpha\)e\(h=a \sin \beta\)
Em seguida, definimos as expressões iguais entre si.
\[\begin{align*} b \sin \alpha&= a \sin \beta\\ \left(\dfrac{1}{ab}\right)\left(b \sin \alpha\right)&= \left(a \sin \beta\right)\left(\dfrac{1}{ab}\right)\qquad \text{Multiply both sides by } \dfrac{1}{ab}\\ \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b} \end{align*}\]
Da mesma forma, podemos comparar as outras proporções.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \gamma}{c}\)e\(\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Coletivamente, essas relações são chamadas de Lei de Sines.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Observe a forma padrão de rotular triângulos: o ângulo\(\alpha\) (alfa) é o lado oposto\(a\); o ângulo\(\beta\) (beta) é o lado oposto\(b\); e o ângulo\(\gamma\) (gama) é o lado oposto\(c\). Veja a Figura\(\PageIndex{6}\).
Ao calcular ângulos e lados, certifique-se de levar os valores exatos até a resposta final. Geralmente, as respostas finais são arredondadas para o décimo mais próximo, a menos que especificado de outra forma.
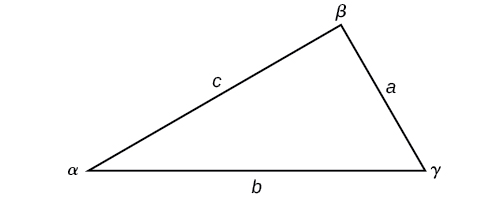
Figura\(\PageIndex{6}\)
Dado um triângulo com ângulos e lados opostos rotulados como na Figura\(\PageIndex{6}\), a razão entre a medição de um ângulo e o comprimento de seu lado oposto será igual às outras duas razões da medida do ângulo em relação ao lado oposto. Todas as proporções serão iguais. A Lei de Sines é baseada em proporções e é apresentada simbolicamente de duas maneiras.
\[\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\]
\[\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\]
Para resolver um triângulo oblíquo, use qualquer par de proporções aplicáveis.
Resolva o triângulo mostrado na Figura\(\PageIndex{7}\) até o décimo mais próximo.
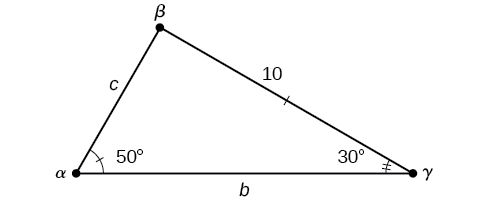
Figura\(\PageIndex{7}\)
Solução
Os três ângulos devem somar 180 graus. A partir disso, podemos determinar que
\[\begin{align*} \beta &= 180^{\circ} - 50^{\circ} - 30^{\circ}\\ &= 100^{\circ} \end{align*}\]
Para encontrar um lado desconhecido, precisamos saber o ângulo correspondente e uma proporção conhecida. Conhecemos esse ângulo\(\alpha=50°\) e seu lado correspondente\(a=10\). Podemos usar a seguinte proporção da Lei de Sines para encontrar o comprimento de\(c\).
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(30^{\circ})}{c}\\ c\dfrac{\sin(50^{\circ})}{10}&= \sin(30^{\circ})\qquad \text{Multiply both sides by } c\\ c&= \sin(30^{\circ})\dfrac{10}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate } c\\ c&\approx 6.5 \end{align*}\]
Da mesma forma, para resolver\(b\), estabelecemos outra proporção.
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(100^{\circ})}{b}\\ b \sin(50^{\circ})&= 10 \sin(100^{\circ})\qquad \text{Multiply both sides by } b\\ b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate }b\\ b&\approx 12.9 \end{align*}\]
Portanto, o conjunto completo de ângulos e lados é
\(\begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\)
Resolva o triângulo mostrado na Figura\(\PageIndex{8}\) até o décimo mais próximo.
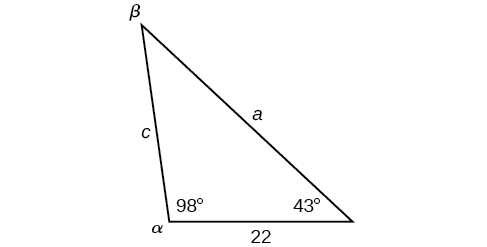
Figura\(\PageIndex{8}\)
- Responda
-
\(\begin{matrix} \alpha=98^{\circ} & a=34.6\\ \beta=39^{\circ} & b=22\\ \gamma=43^{\circ} & c=23.8 \end{matrix}\)
Usando a Lei de Sines para resolver triângulos SSA
Podemos usar a Lei de Sines para resolver qualquer triângulo oblíquo, mas algumas soluções podem não ser simples. Em alguns casos, mais de um triângulo pode satisfazer os critérios fornecidos, o que descrevemos como um caso ambíguo. Triângulos classificados como SSA, aqueles nos quais conhecemos o comprimento de dois lados e a medição do ângulo oposto a um dos lados dados, podem resultar em uma ou duas soluções, ou mesmo em nenhuma solução.
Triângulos oblíquos na categoria SSA podem ter quatro resultados diferentes. A figura\(\PageIndex{9}\) ilustra as soluções com os lados\(a\)\(b\) e ângulos conhecidos\(\alpha\).
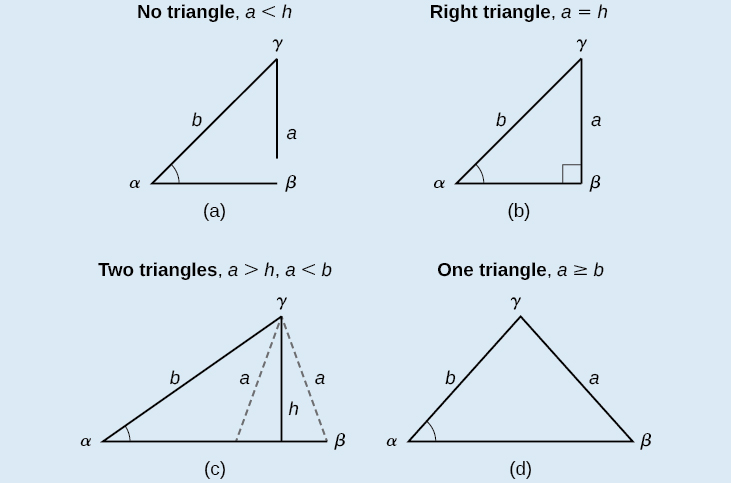
Figura\(\PageIndex{9}\)
Resolva o triângulo na Figura\(\PageIndex{10}\) para o lado que falta e encontre as medidas do ângulo que faltam até o décimo mais próximo.
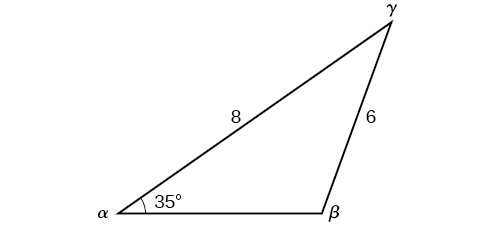
Figura\(\PageIndex{10}\)
Solução
Use a Lei de Sines para encontrar o ângulo\(\beta\) e o ângulo\(\gamma\), e depois o lado\(c\). Resolvendo para\(\beta\), temos a proporção
\[\begin{align*} \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b}\\ \dfrac{\sin(35^{\circ})}{6}&= \dfrac{\sin \beta}{8}\\ \dfrac{8 \sin(35^{\circ})}{6}&= \sin \beta\\ 0.7648&\approx \sin \beta\\ {\sin}^{-1}(0.7648)&\approx 49.9^{\circ}\\ \beta&\approx 49.9^{\circ} \end{align*}\]
No entanto, no diagrama, o ângulo\(\beta\) parece ser um ângulo obtuso e pode ser maior que\(90°\). Como obtivemos um ângulo agudo e como encontramos a medida de\(\beta\)? Vamos investigar mais a fundo. Soltando uma perpendicular\(\gamma\) e vendo o triângulo de uma perspectiva de ângulo reto, temos a Figura\(\PageIndex{11}\). Parece que pode haver um segundo triângulo que atenda aos critérios fornecidos.
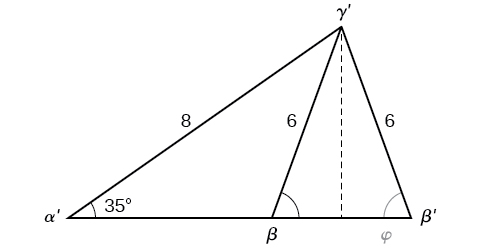
Figura\(\PageIndex{11}\)
O ângulo suplementar a\(\beta\) é aproximadamente igual a\(49.9°\), o que significa que\(\beta=180°−49.9°=130.1°\). (Lembre-se de que a função seno é positiva no primeiro e no segundo quadrantes.) Resolvendo para\(\gamma\), temos
\[\begin{align*} \gamma&= 180^{\circ}-35^{\circ}-130.1^{\circ}\\ &\approx 14.9^{\circ} \end{align*}\]
Podemos então usar essas medidas para resolver o outro triângulo. Uma vez que\(\beta′\) é complementar a\(\beta\), temos
\[\begin{align*} \gamma^{'}&= 180^{\circ}-35^{\circ}-49.5^{\circ}\\ &\approx 95.1^{\circ} \end{align*}\]
Agora precisamos encontrar\(c\)\(c′\) e.
Nós temos
\[\begin{align*} \dfrac{c}{\sin(14.9^{\circ})}&= \dfrac{6}{\sin(35^{\circ})}\\ c&= \dfrac{6 \sin(14.9^{\circ})}{\sin(35^{\circ})}\\ &\approx 2.7 \end{align*}\]
Finalmente,
\[\begin{align*} \dfrac{c'}{\sin(95.1^{\circ})}&= \dfrac{6}{\sin(35^{\circ})}\\ c'&= \dfrac{6 \sin(95.1^{\circ})}{\sin(35^{\circ})}\\ &\approx 10.4 \end{align*}\]
Para resumir, existem dois triângulos com um ângulo de\(35°\), um lado adjacente de 8 e um lado oposto de 6, conforme mostrado na Figura\(\PageIndex{12}\).
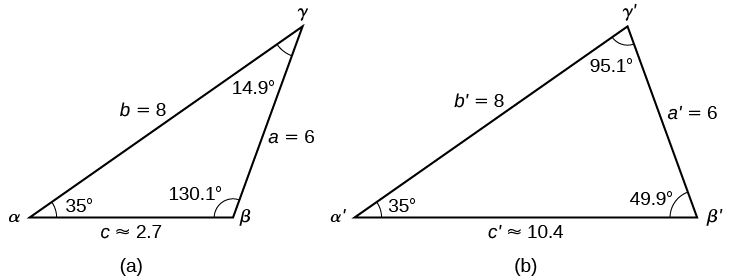
Figura\(\PageIndex{12}\)
No entanto, estávamos procurando os valores para o triângulo com um ângulo obtuso\(\beta\). Podemos vê-los no primeiro triângulo (a) na Figura\(\PageIndex{12}\).
Dado\(\alpha=80°\),\(a=120\), e\(b=121\), encontre o lado e os ângulos que faltam. Se houver mais de uma solução possível, mostre ambas.
- Responda
-
Solução 1
\(\begin{matrix} \alpha=80^{\circ} & a=120\\ \beta\approx 83.2^{\circ} & b=121\\ \gamma\approx 16.8^{\circ} & c\approx 35.2 \end{matrix}\)
Solução 2
\(\begin{matrix} \alpha '=80^{\circ} & a'=120\\ \beta '\approx 96.8^{\circ} & b'=121\\ \gamma '\approx 3.2^{\circ} & c'\approx 6.8 \end{matrix}\)
No triângulo mostrado na Figura\(\PageIndex{13}\), resolva o lado e os ângulos desconhecidos. Arredonde suas respostas para o décimo mais próximo.
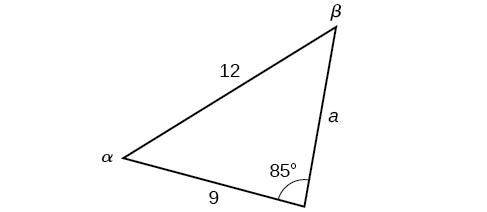
Figura\(\PageIndex{13}\)
Solução
Ao escolher o par de rácios da Lei de Sines a usar, veja as informações fornecidas. Nesse caso, conhecemos o ângulo\(\gamma=85°\), e seu lado correspondente\(c=12\), e conhecemos o lado\(b=9\). Usaremos essa proporção para resolver\(\beta\).
\[\begin{align*} \dfrac{\sin(85^{\circ})}{12}&= \dfrac{\sin \beta}{9}\qquad \text{Isolate the unknown.}\\ \dfrac{9 \sin(85^{\circ})}{12}&= \sin \beta \end{align*}\]
Para encontrar\(\beta\), aplique a função senoidal inversa. O seno inverso produzirá um único resultado, mas lembre-se de que pode haver dois valores para\(\beta\). É importante verificar o resultado, pois pode haver duas soluções viáveis, apenas uma solução (o caso usual) ou nenhuma solução.
\[\begin{align*} \beta&= {\sin}^{-1}\left(\dfrac{9 \sin(85^{\circ})}{12}\right)\\ \beta&\approx {\sin}^{-1} (0.7471)\\ \beta&\approx 48.3^{\circ} \end{align*}\]
Nesse caso, se subtrairmos\(\beta\) de\(180°\), descobrimos que pode haver uma segunda solução possível. Assim,\(\beta=180°−48.3°≈131.7°\). Para verificar a solução, subtraia os dois ângulos\(131.7°\) e\(85°\), de\(180°\). Isso dá
\[\begin{align*} \alpha&= 180^{\circ}-85^{\circ}-131.7^{\circ}\\ &\approx -36.7^{\circ} \end{align*}\]
o que é impossível, e assim por diante\(\beta≈48.3°\).
Para encontrar os valores faltantes restantes, calculamos\(\alpha=180°−85°−48.3°≈46.7°\). Agora, o único lado\(a\) é necessário. Use a Lei de Sines para resolver\(a\) por uma das proporções.
\[\begin{align*} \dfrac{\sin(85°)}{12}&= \dfrac{\sin(46.7^{\circ})}{a}\\ a\dfrac{\sin(85^{\circ})}{12}&= \sin(46.7^{\circ})\\ a&=\dfrac{12\sin(46.7^{\circ})}{\sin(85^{\circ})}\\ &\approx 8.8 \end{align*}\]
O conjunto completo de soluções para o triângulo dado é
\(\begin{matrix} \alpha\approx 46.7^{\circ} & a\approx 8.8\\ \beta\approx 48.3^{\circ} & b=9\\ \gamma=85^{\circ} & c=12 \end{matrix}\)
Dado\(\alpha=80°\),\(a=100\),\(b=10\), encontre o lado e os ângulos que faltam. Se houver mais de uma solução possível, mostre ambas. Arredonde suas respostas para o décimo mais próximo.
- Responda
-
\(\beta≈5.7°\),\(\gamma≈94.3°\),\(c≈101.3\)
Encontre todos os triângulos possíveis se um lado tiver comprimento\(4\) oposto a um ângulo de\(50°\) e um segundo lado tiver comprimento\(10\).
Solução
Usando as informações fornecidas, podemos resolver o ângulo oposto ao lado do comprimento\(10\). Veja a Figura\(\PageIndex{14}\).
\[\begin{align*} \dfrac{\sin \alpha}{10}&= \dfrac{\sin(50^{\circ})}{4}\\ \sin \alpha&= \dfrac{10 \sin(50^{\circ})}{4}\\ \sin \alpha&\approx 1.915 \end{align*}\]
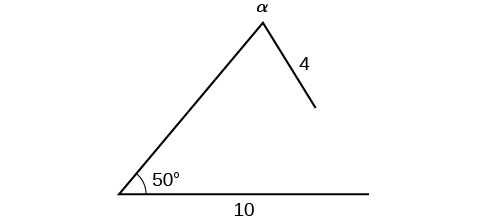
Figura\(\PageIndex{14}\)
Podemos parar aqui sem encontrar o valor de\(\alpha\). Como o alcance da função seno é\([ −1,1 ]\), é impossível que o valor do seno seja\(1.915\). Na verdade, inserir\({\sin}^{−1}(1.915)\) em uma calculadora gráfica gera um DOMÍNIO DE ERRO. Portanto, nenhum triângulo pode ser desenhado com as dimensões fornecidas.
Determine o número de triângulos possíveis dado\(a=31\),\(b=26\),\(\beta=48°\).
- Responda
-
dois
Encontrando a área de um triângulo oblíquo usando a função seno
Agora que podemos resolver um triângulo para valores faltantes, podemos usar alguns desses valores e a função seno para encontrar a área de um triângulo oblíquo. Lembre-se de que a fórmula da área para um triângulo é dada como\(Area=\dfrac{1}{2}bh\), onde\(b\) é base e\(h\) é altura. Para triângulos oblíquos, precisamos encontrar\(h\) antes de podermos usar a fórmula da área. Observando os dois triângulos na Figura\(\PageIndex{15}\), um agudo e outro obtuso, podemos soltar uma perpendicular para representar a altura e, em seguida, aplicar a propriedade trigonométrica\(\sin \alpha=\dfrac{opposite}{hypotenuse}\) para escrever uma equação para a área em triângulos oblíquos. No triângulo agudo, temos\(\sin \alpha=\dfrac{h}{c}\) ou\(c \sin \alpha=h\). No entanto, no triângulo obtuso, soltamos a perpendicular para fora do triângulo e estendemos a base\(b\) para formar um triângulo reto. O ângulo usado no cálculo é\(\alpha′\), ou\(180−\alpha\).
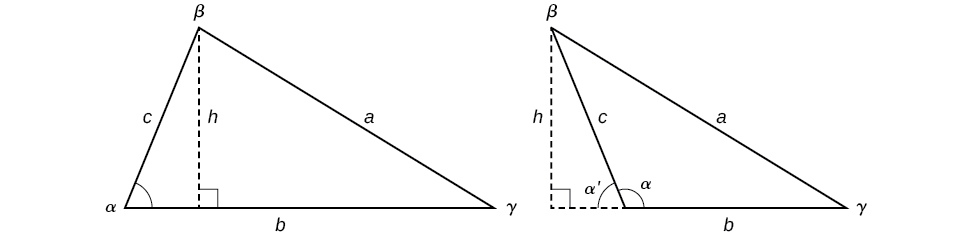
Figura\(\PageIndex{15}\)
Assim,
\(Area=\dfrac{1}{2}(base)(height)=\dfrac{1}{2}b(c \sin \alpha)\)
Da mesma forma,
\(Area=\dfrac{1}{2}a(b \sin \gamma)=\dfrac{1}{2}a(c \sin \beta)\)
A fórmula para a área de um triângulo oblíquo é dada por
\[Area=\dfrac{1}{2}bc \sin \alpha\]
\[Area=\dfrac{1}{2}ac \sin \beta\]
\[Area=\dfrac{1}{2}ab \sin \gamma\]
Isso equivale a metade do produto dos dois lados e ao seno do ângulo incluído.
Encontre a área de um triângulo com lados\(a=90\)\(b=52\), e ângulo\(\gamma=102°\). Arredonde a área para o número inteiro mais próximo.
Solução
Usando a fórmula, temos
\[\begin{align*} Area&= \dfrac{1}{2}ab \sin \gamma\\ Area&= \dfrac{1}{2}(90)(52) \sin(102^{\circ})\\ Area&\approx 2289\; \text{square units} \end{align*}\]
Encontre a área do triângulo dada\(\beta=42°\),\(a=7.2 ft\),\(c=3.4 ft\). Arredonde a área até o décimo mais próximo.
- Responda
-
cerca de pés\(8.2\) quadrados
Resolvendo problemas aplicados usando a Lei de Sines
Quanto mais estudamos as aplicações trigonométricas, mais descobrimos que as aplicações são incontáveis. Algumas são situações planas do tipo diagrama, mas muitas aplicações em cálculo, engenharia e física envolvem três dimensões e movimento.
Encontre a altitude da aeronave no problema apresentado no início desta seção, mostrado na Figura\(\PageIndex{16}\). Arredonde a altitude até o décimo de milha mais próximo.
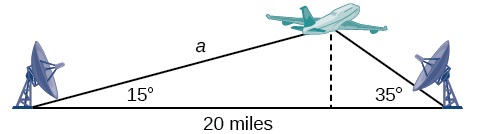
Figura\(\PageIndex{16}\)
Solução
Para encontrar a elevação da aeronave, primeiro encontramos a distância de uma estação até a aeronave, como a lateral\(a\), e depois usamos as relações do triângulo reto para encontrar a altura da aeronave,\(h\).
Como os ângulos no triângulo somam\(180\) graus, o ângulo desconhecido deve ser\(180°−15°−35°=130°\). Este ângulo é oposto ao lado do comprimento\(20\), o que nos permite estabelecer uma relação da Lei de Sines.
\[\begin{align*} \dfrac{\sin(130^{\circ})}{20}&= \dfrac{\sin(35^{\circ})}{a}\\ a \sin(130^{\circ})&= 20 \sin(35^{\circ})\\ a&= \dfrac{20 \sin(35^{\circ})}{\sin(130^{\circ})}\\ a&\approx 14.98 \end{align*}\]
A distância de uma estação até a aeronave é de cerca de\(14.98\) milhas.
Agora que sabemos\(a\), podemos usar relacionamentos de triângulo reto para resolver\(h\).
\[\begin{align*} \sin(15^{\circ})&= \dfrac{opposite}{hypotenuse}\\ \sin(15^{\circ})&= \dfrac{h}{a}\\ \sin(15^{\circ})&= \dfrac{h}{14.98}\\ h&= 14.98 \sin(15^{\circ})\\ h&\approx 3.88 \end{align*}\]
A aeronave está a uma altitude de aproximadamente\(3.9\) milhas.
O diagrama mostrado na Figura\(\PageIndex{17}\) representa a altura de um dirigível sobrevoando um estádio de futebol. Encontre a altura do dirigível se o ângulo de elevação na zona do extremo sul, ponto A, for\(70°\), o ângulo de elevação da zona da extremidade norte, ponto B, for\(62°\), e a distância entre os pontos de visualização das duas zonas extremas for\(145\) jardas.
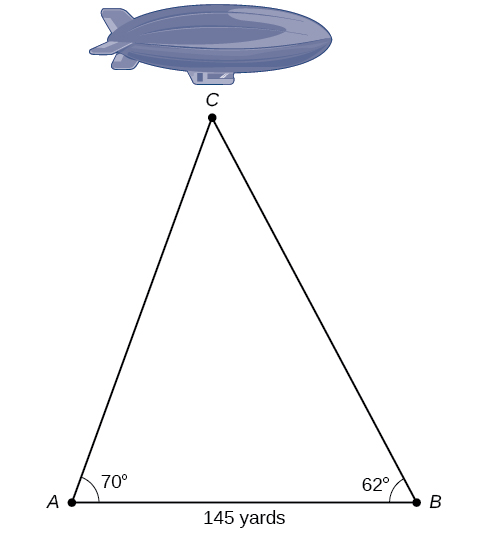
Figura\(\PageIndex{17}\)
- Responda
-
\(161.9\)yd.
Mídia
Acesse esses recursos on-line para obter instruções e práticas adicionais com aplicativos trigonométricos.
Equações-chave
| Lei de Sines |
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\) \(\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\) |
| Área para triângulos oblíquos |
\(Area=\dfrac{1}{2}bc \sin \alpha\) \(=\dfrac{1}{2} ac \sin \beta\) \(=\dfrac{1}{2} ab \sin \gamma\) |
Conceitos-chave
- A Lei de Sines pode ser usada para resolver triângulos oblíquos, que não são triângulos retos.
- De acordo com a Lei de Sines, a razão entre a medição de um dos ângulos e o comprimento de seu lado oposto é igual às outras duas razões da medida do ângulo em relação ao lado oposto.
- Há três casos possíveis: ASA, AAS, SSA. Dependendo das informações fornecidas, podemos escolher a equação apropriada para encontrar a solução solicitada. Veja o exemplo\(\PageIndex{1}\).
- O caso ambíguo surge quando um triângulo oblíquo pode ter resultados diferentes.
- Há três casos possíveis decorrentes do acordo de SSA — uma única solução, duas soluções possíveis e nenhuma solução. Veja o exemplo\(\PageIndex{2}\) e o exemplo\(\PageIndex{3}\).
- A Lei de Sines pode ser usada para resolver triângulos com determinados critérios. Veja o exemplo\(\PageIndex{4}\).
- A fórmula de área geral para triângulos se traduz em triângulos oblíquos ao encontrar primeiro o valor de altura apropriado. Veja o exemplo\(\PageIndex{5}\).
- Há muitas aplicações trigonométricas. Muitas vezes, eles podem ser resolvidos primeiro desenhando um diagrama das informações fornecidas e, em seguida, usando a equação apropriada. Veja o exemplo\(\PageIndex{6}\).


