7.R: Identidades e equações trigonométricas (Revisão)

Last updated
Save as PDF

Page ID: 189350

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

7.1: Resolvendo equações trigonométricas com identidades

Para os exercícios 1-6, encontre exatamente todas as soluções que existem no intervalo$[0,2\pi )$.

1)$\csc ^2 t=3$

Resposta: $\sin^{-1}\left ( \dfrac{\sqrt{3}}{3} \right ), \pi -\sin^{-1}\left ( \dfrac{\sqrt{3}}{3} \right ), \pi +\sin^{-1}\left ( \dfrac{\sqrt{3}}{3} \right ), 2\pi -\sin^{-1}\left ( \dfrac{\sqrt{3}}{3} \right )$

2)$\cos ^2 x=\dfrac{1}{4}$

3)$2\sin \theta =-1$

Resposta: $\dfrac{7\pi }{6}, \dfrac{11\pi }{6}$

4)$\tan x \sin x+\sin(-x)=0$

5)$9\sin \omega -2=4\sin^2 \omega$

Resposta: $\sin^{-1}\left ( \dfrac{1}{4} \right ), \pi -\sin^{-1}\left ( \dfrac{1}{4} \right )$

6)$1-2\tan(\omega )=\tan^2(\omega )$

Para os exercícios 7-8, use identidades básicas para simplificar a expressão.

7)$\sec x \cos x+\cos x-\dfrac{1}{\sec x}$

Resposta: $1$

8)$\sin^3 x+\cos^2 x \sin x$

Para os exercícios 9-10, determine se as identidades fornecidas são equivalentes.

9)$\sin^2 x+\sec^2 x -1=\dfrac{(1-\cos ^2 x)(1+\cos ^2 x)}{\cos ^2 x}$

Resposta: sim

10)$\tan^3 x \csc^2 x \cot^2 x \cos x \sin x=1$

7.2: Identidades de soma e diferença

Para os exercícios 1-4, encontre o valor exato.

1)$\tan \left (\dfrac{7\pi }{12} \right )$

Resposta: $-2-\sqrt{3}$

2)$\cos \left (\dfrac{25\pi }{12} \right )$

3)$\sin(70^{\circ})\cos(25^{\circ})-\cos(70^{\circ})\sin(25^{\circ})$

Resposta: $\dfrac{\sqrt{2}}{2}$

4)$\cos(83^{\circ})\cos(23^{\circ})+\sin(83^{\circ})\sin(23^{\circ})$

Para os exercícios 5-6, prove a identidade.

5)$\cos(4x)-\cos(3x)\cos x=\sin^2 x-4\cos^2 x \sin^2 x$

Resposta: \ (\ begin {align*}
\ cos (4x) -\ cos (3x)\ cos x &=\ cos (2x+2x) -\ cos (x+2x)\ cos x\\
&=\ cos (2x)\ cos (2x) -\ sin (2x)\ sin (2x) -\ cos x\ cos (2x)\ cos x+\ sin x\ sin (2x)\ cos x\\
&= (\ cos ^2 x-\ sin ^2 x) ^2-4\ cos ^2 x\ sin ^2 x-\ cos ^2 x (\ cos ^2
x-\ sin ^2 x) +\ sin x (2)\ sin x\ cos x\ cos x\\
&= (\ cos ^2 x-\ sin ^2 x) ^2-4\ cos ^2 x\ sin ^2 x-\ cos ^2 x (\ cos ^2 x-\ sin ^2 x) +2\ sin ^2 x\ cos ^2 x\\
&=\ cos ^4x-2\ cos^2x\ sin^2x+\ sin ^4-\ cos^2x\ sin^2x-\ cos^4x+\ cos^2x\ sin^2x+2\ sin^2x\ cos^2x\\
&= \ sin^4x-4\ cos^2x\ sin^2x+\ cos^2x\ sin^2x\\
&=\ sin^2x (\ sin^2x+\ cos^2x) -4\ cos^2x\ sin^2x\\
&=\ sin^2 x-4\ cos^2 x\ sin^2 x
\ end {alinhamento*}\)

6)$\cos(3x)-\cos^3x=-\cos x \sin^2x-\sin x \sin(2x)$

Para o exercício 7, simplifique a expressão.

7)$\dfrac{\tan \left ( \tfrac{1}{2}x \right )+\tan \left ( \tfrac{1}{8}x \right )}{1-\tan \left ( \tfrac{1}{8}x \right )\tan \left ( \tfrac{1}{2}x \right )}$

Resposta: $\tan \left ( \dfrac{5}{8}x \right )$

Para os exercícios 8-9, encontre o valor exato.

8)$\cos \left ( \sin^{-1}(0)-\cos^{-1}\left ( \dfrac{1}{2} \right ) \right )$

9)$\tan \left ( \sin^{-1}(0)-\sin^{-1}\left ( \dfrac{1}{2} \right ) \right )$

Resposta: $\dfrac{\sqrt{3}}{3}$

7.3: Fórmulas de ângulo duplo, meio ângulo e redução

Para os exercícios 1-4, encontre o valor exato.

1) Encontre$\sin (2\theta )$,$\cos (2\theta )$,e$\tan (2\theta )$ dado$\cos \theta =-\dfrac{1}{3}$ e$\theta $ está no intervalo$\left [\dfrac{\pi }{2} , \pi \right ]$.

2) Encontre$\sin (2\theta )$$\cos (2\theta )$, e$\tan (2\theta )$$\sec \theta =-\dfrac{5}{3}$ forneça e$\theta $ esteja no intervalo$\left [\dfrac{\pi }{2} , \pi \right ]$.

Resposta: $-\dfrac{24}{25}, -\dfrac{7}{25}, \dfrac{24}{7}$

3)$\sin \left (\dfrac{7\pi }{8} \right )$

4)$\sec \left (\dfrac{3\pi }{8} \right )$

Resposta: $\sqrt{2(2+\sqrt{2})}$

Para os exercícios 5-6, use a Figura abaixo para encontrar as quantidades desejadas.

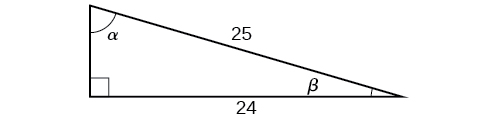
$CNX_Precalc_Figure_07_07_201.jpg$

5)$\sin(2\beta ),\cos(2\beta ),\tan(2\beta ),\sin(2\alpha ),\cos(2\alpha ),\tan(2\alpha )$

6)$\sin \left (\frac{\beta }{2} \right ) ,\cos\left (\frac{\beta }{2} \right ),\tan\left (\frac{\beta }{2} \right ),\sin\left (\frac{\alpha }{2} \right ),\cos\left (\frac{\alpha }{2} \right ),\tan\left (\frac{\alpha }{2} \right )$

Resposta: $\dfrac{\sqrt{2}}{10},\dfrac{7\sqrt{2}}{10},\dfrac{1}{7},\dfrac{3}{5},\dfrac{4}{5},\dfrac{3}{4}$

Para os exercícios 7-8, prove a identidade.

7)$\dfrac{2\cos (2x)}{\sin (2x)}=\cot x-\tan x$

8)$\cot x \cos (2x) = -\sin (2x)+\cot x$

Resposta: $\begin{align*} \cot x \cos (2x) &= \cot x(1-2\sin ^2 x)\\ &= \cot x-\dfrac{\cos x}{\sin x}(2)\sin ^2 x\\ &= -2\sin x \cos \\ &= -\sin (2x)+\cot x \end{align*}$

Para os exercícios 9-10, reescreva a expressão sem poderes.

9)$\cos ^2 x \sin ^4 (2x)$

10)$\tan ^2 x \sin ^3 x$

Resposta: $\dfrac{10\sin x-5\sin (3x)+\sin (5x)}{8(\cos (2x)+1)}$

7.4: Fórmulas de soma para produto e produto para soma

Para os exercícios 1-3, avalie o produto para a expressão dada usando uma soma ou diferença de duas funções. Escreva a resposta exata.

1)$\cos \left ( \dfrac{\pi }{3} \right )\sin \left ( \dfrac{\pi }{4} \right )$

2)$2\sin \left ( \dfrac{2\pi }{3} \right )\sin \left ( \dfrac{5\pi }{6} \right )$

Resposta: $\dfrac{\sqrt{3}}{2}$

3)$2\cos \left ( \dfrac{\pi }{5} \right )\cos \left ( \dfrac{\pi }{3} \right )$

Para os exercícios 4-5, avalie a soma usando uma fórmula de produto. Escreva a resposta exata.

4)$\sin \left ( \dfrac{\pi }{12} \right )-\sin \left ( \dfrac{7\pi }{12} \right )$

Resposta: $-\dfrac{\sqrt{2}}{2}$

5)$\cos \left ( \dfrac{5\pi }{12} \right )+\cos \left ( \dfrac{7\pi }{12} \right )$

Para os exercícios 6-9, altere as funções de um produto para uma soma ou de uma soma para um produto.

6)$\sin(9x)\cos(3x)$

Resposta: $\dfrac{1}{2}(\sin(6x)+\sin(12x))$

7)$\cos(7x)\cos(12x)$

8)$\sin(11x)+\sin(2x)$

Resposta: $2\sin \left (\dfrac{13}{2}x \right )\cos \left (\dfrac{9}{2}x \right )$

9)$\cos(6x)+\cos(5x)$

7.5: Resolvendo equações trigonométricas

Para os exercícios 1-2, encontre todas as soluções exatas no intervalo$[0,2\pi )$.

1)$\tan x+1=0$

Resposta: $\dfrac{3\pi }{4}, \dfrac{7\pi }{4}$

2)$2\sin(2x)+\sqrt{2}=0$

Para os exercícios 3-7, encontre todas as soluções exatas no intervalo$[0,2\pi )$.

3)$2\sin^2 x-\sin x=0$

Resposta: $0, \dfrac{\pi }{6}, \dfrac{5\pi }{6}, \pi $

4)$\cos^2 x-\cos x -1=0$

5)$2\sin^2 x+5\sin x +3=0$

Resposta: $\dfrac{3\pi }{2}$

6)$\cos x - 5\sin(2x)=0$

7)$\dfrac{1}{\sec ^2 x}+2+\sin^2 x+4\cos ^2 x=0$

Resposta: Sem solução.

Para os exercícios 8-9, simplifique a equação algebricamente o máximo possível. Em seguida, use uma calculadora para encontrar as soluções no intervalo$[0,2\pi )$. Arredonde para quatro casas decimais.

8)$\sqrt{3}\cot ^2 x+\cot x=1$

9)$\csc ^2 x-3\csc x-4=0$

Resposta: $0.2527,2.8889,4.7124$

Para os exercícios 10-11, represente graficamente cada lado da equação para encontrar os zeros no intervalo$[0,2\pi )$.

10)$20\cos^2x+21\cos x+1=0$

11)$\sec^2x-2\sec x=15$

Resposta: $1.3694, 1.9106, 4.3726, 4.9137$

7.6: Modelagem com equações trigonométricas

Para os exercícios 1-3, faça um gráfico dos pontos e encontre uma possível fórmula para os valores trigonométricos na tabela fornecida.

$x$	0	1	2	3	4	5
$y$	1	6	11	6	1	6

$x$	$y$
\ (x\) ">0	\ (y\) ">-2
\ (x\) ">1	\ (y\) ">1
\ (x\) ">2	\ (y\) ">-2
\ (x\) ">3	\ (y\) ">-5
\ (x\) ">4	\ (y\) ">-2
\ (x\) ">5	\ (y\) ">1

Resposta: $3\sin \left ( \dfrac{x\pi }{2} \right )-2$

$x$	$y$
\ (x\) ">-3	\ (y\) ">$3+2\sqrt{2}$
\ (x\) ">-2	\ (y\) ">3
\ (x\) ">-1	\ (y\) ">$2\sqrt{2}-1$
\ (x\) ">0	\ (y\) ">1
\ (x\) ">1	\ (y\) ">$3-2\sqrt{2}$
\ (x\) ">2	\ (y\) ">-1
\ (x\) ">3	\ (y\) ">$-1-2\sqrt{2}$

4) Um homem com$6$ os pés na altura dos olhos acima do solo está a poucos$3$ metros da base de uma escada vertical$15$ de um metro. Se ele olhar para o topo da escada, em que ângulo acima da horizontal ele está olhando?

Resposta: $71.6^{\circ}$

5) Usando a escada do exercício anterior, se um trabalhador da construção civil$6$ de um metro de altura parado no topo da escada olhar para os pés do homem parado na parte inferior, que ângulo da horizontal ele está olhando?

Para os exercícios 6-7, construa funções que modelem o comportamento descrito.

6) A população de lemingues varia com uma baixa anual$500$ de março. Se a população média anual de lemingues for$950$, escreva uma função que modela a população em relação a$t$,o mês.

Resposta: $P(t)=950-450\sin \left ( \dfrac{\pi }{6}t \right )$

7) As temperaturas diárias no deserto podem ser muito extremas. Se a temperatura variar de$90^{\circ}$ F a$30^{\circ}$ F e a temperatura média diária ocorrer pela primeira vez às 10h, escreva uma função modelando esse comportamento.

Para os exercícios 8-9, determine a amplitude, a frequência e o período das equações dadas.

8)$y=3\cos(x\pi )$

Resposta: Amplitude:$3$, período:$2$, frequência:$\dfrac{1}{2}$ Hz

9)$y=-2\sin(16x\pi )$

Para os exercícios 10-11, modele o comportamento descrito e encontre os valores solicitados.

10) Uma espécie invasora de carpa é introduzida no Lago de Água Doce. Inicialmente, há$100$ carpas no lago e a população varia de acordo com os$20$ peixes sazonalmente. Se por ano$5$, houver$625$ carpas, encontre uma função modelando a população de carpas em relação a$t$,o número de anos a partir de agora.

Resposta: $C(t)=20\sin (2\pi t)+100(1.4427)^t$

11) A população de peixes nativos de Lake Freshwater calcula a média de$2500$ peixes, variando de acordo com os$100$ peixes sazonalmente. Devido à competição por recursos da carpa invasora, espera-se que a população de peixes nativos diminua a$5\%$ cada ano. Encontre uma função modelando a população de peixes nativos em relação a$t$,o número de anos a partir de agora. Também determine quantos anos a carpa levará para ultrapassar a população de peixes nativos.

Teste prático

Para os exercícios 1-2, simplifique a expressão dada.

1)$\cos(-x)\sin x \cot x+\sin^2x$

Resposta: $1$

2)$\sin(-x)\cos(-2x)-\sin(-x)\cos(-2x)$

Para os exercícios 3-6, encontre o valor exato.

3)$\cos \left ( \dfrac{7\pi }{12} \right )$

Resposta: $\dfrac{\sqrt{2}-\sqrt{6}}{4}$

4)$\tan \left ( \dfrac{3\pi }{8} \right )$

5)$\tan \left (\sin^{-1}\left (\dfrac{\sqrt{2}}{2} \right )+\tan^{-1}\sqrt{3} \right )$

Resposta: $-\sqrt{2}-\sqrt{3}$

6)$2\sin \left (\dfrac{\pi }{4} \right )\sin \left (\dfrac{\pi }{6} \right )$

Para os exercícios 7-16, encontre todas as soluções exatas para a equação em$[0,2\pi )$.

7)$\cos^2x-\sin^2x-1=0$

Resposta: $0, \pi $

8)$\cos^2x=\cos x$

Resposta: $\sin^{-1}\left (\dfrac {1}{4}\left(\sqrt{13}-1\right) \right ), \pi - \sin^{-1}\left (\dfrac {1}{4}\left(\sqrt{13}-1\right) \right )$

9)$\cos (2x)+\sin ^2 x = 0$

10)$2\sin ^2 x - \sin x = 0$

Resposta: $0, \dfrac{\pi }{6}, \dfrac{5\pi }{6}, \pi$

11) Reescreva a expressão como um produto em vez de uma soma:$\cos (2x)+\cos (-8x)$

12) Encontre todas as soluções do$\tan (x)-\sqrt{3}=0$.

Resposta: $\dfrac{\pi }{3}+k\pi$

13) Encontre as soluções de$\sec ^2x -2\sec x=15$ no intervalo$[0,2\pi )$ algebricamente; em seguida, represente graficamente os dois lados da equação para determinar a resposta.

14) Encontre$\sin (2\theta )$,$\cos (2\theta )$, e$\tan (2\theta )$$\cot \theta =-\dfrac{3}{4}$ forneça e$\theta $ está no intervalo$\left [ \dfrac{\pi }{2}, \pi \right ]$.

Resposta: $-\dfrac{24}{25}, -\dfrac{7}{25}, \dfrac{24}{7}$

15) Encontre$\sin \left (\dfrac{\theta }{2} \right )$,$\cos \left (\dfrac{\theta }{2} \right )$, e$\tan \left (\dfrac{\theta }{2} \right )$ forneça$\cos \theta =-\dfrac{7}{25}$ e$\theta $ está no quadrante$\mathrm{IV}$.

16) Reescreva a expressão$\sin ^4 x$ sem poderes maiores que$1$.

Resposta: $\dfrac{1}{8}(3+\cos (4x)-4\cos (2x))$

Para os exercícios 17-19, prove a identidade.

17)$\tan^3x-\tan x \sec^2x=\tan(-x)$

18)$\sin(3x)-\cos x \sin(2x)=\cos^2x \sin x-\sin^3x$

Resposta: $\begin{align*} \sin(3x)-\cos x \sin(2x) &= \\ \sin(x+2x)-\cos x(2\sin x \cos x) &= \\ \sin x \cos(2x)+\sin(2x)\cos x -2\sin x \cos ^2x &= \\ \sin x(\cos ^2x - \sin ^2x)+2\sin x \cos x \cos x - 2\sin x \cos ^2x &= \\ \sin x \cos ^2x - \sin ^3x +0 &= \\ \cos^2x \sin x - \sin ^3x &= \cos^2x \sin x-\sin^3x \end{align*}$

19)$\dfrac{\sin (2x)}{\sin x}-\dfrac{\cos (2x)}{\cos x}=\sec x$

20) Faça um gráfico dos pontos e encontre uma função do formulário$y=A\cos(Bx+C)+D$ que se ajuste aos dados fornecidos.

$x$	0	1	2	3	4	5
$y$	-2	2	-2	2	-2	2

Resposta: $y=2\cos(\pi x+\pi )$

21) O deslocamento$h(t)$ em centímetros de uma massa suspensa por uma mola é modelado pela função$h(t)=\dfrac{1}{4}\sin (120\pi t)$,onde$t$ é medido em segundos. Encontre a amplitude, o período e a frequência desse deslocamento.

22) Uma mulher está a poucos$300$ metros de distância de um prédio$2000$ de pés. Se ela olhar para o topo do prédio, em que ângulo acima da horizontal ela está olhando? Um trabalhador entediado olha para ela do ^15º andar ($1500$pés acima dela). Em que ângulo ele está olhando para ela? Arredonde para o décimo de grau mais próximo.

Resposta: $81.5^{\circ}, 78.7^{\circ}$

23) Duas frequências de som são tocadas em um instrumento regido pela equação$n(t)=8\cos(20\pi t)\cos(1000\pi t)$. Quais são o período e a frequência das oscilações “rápidas” e “lentas”? Qual é a amplitude?

24) A queda de neve média mensal em uma pequena vila no Himalaia é de$6$ polegadas, com a baixa de$1$ polegada ocorrendo em julho. Construa uma função que modela esse comportamento. Durante qual período há mais de$10$ centímetros de neve?

Resposta: $6+5\cos \left ( \dfrac{\pi }{6}(1-x) \right )$. De 23 de novembro a 6 de fevereiro.

25) Uma mola presa a um teto é puxada para baixo em$20$ cm. Depois de$3$ segundos, em que completa períodos$6$ completos, a amplitude é de apenas$15$ cm. Encontre a função que modela a posição da mola$t$ segundos após ser liberada. A que horas a primavera vai descansar? Nesse caso, use a amplitude de$1$ cm como repouso.

26) Os níveis de água próximos a uma geleira atualmente têm uma média de$9$ pés, variando sazonalmente em$2$ polegadas acima e abaixo da média e atingindo seu ponto mais alto em janeiro. Devido ao aquecimento global, a geleira começou a derreter mais rápido do que o normal. Todos os anos, os níveis da água sobem em$3$ centímetros constantes. Encontre uma função que modele a profundidade da água daqui a$t$ meses. Se as docas estiverem$2$ pés acima dos níveis atuais da água, em que ponto a água subirá primeiro acima das docas?

Resposta: $D(t)=2\cos \left ( \dfrac{\pi }{6}t \right )+108+\dfrac{1}{4}t$,$93.5855$ meses (ou$7.8$ anos) a partir de agora

Contribuidores e atribuições

Template:OpenStaxPreCalc

\(x\)	\(y\)
\ (x\) ">-3	\ (y\) ">\(3+2\sqrt{2}\)
\ (x\) ">-2	\ (y\) ">3
\ (x\) ">-1	\ (y\) ">\(2\sqrt{2}-1\)
\ (x\) ">0	\ (y\) ">1
\ (x\) ">1	\ (y\) ">\(3-2\sqrt{2}\)
\ (x\) ">2	\ (y\) ">-1
\ (x\) ">3	\ (y\) ">\(-1-2\sqrt{2}\)