2.2: Gráficos de funções lineares

Last updated
Save as PDF

Page ID: 189308

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Grafe funções lineares.
Escreva a equação para uma função linear a partir do gráfico de uma linha.
Dadas as equações de duas retas, determine se seus gráficos são paralelos ou perpendiculares.
Escreva a equação de uma reta paralela ou perpendicular a uma determinada linha.
Resolva um sistema de equações lineares.

Duas companhias telefônicas concorrentes oferecem planos de pagamento diferentes. Os dois planos cobram a mesma tarifa por minuto de longa distância, mas cobram uma taxa fixa mensal diferente. Um consumidor quer determinar se os dois planos custarão a mesma quantia por um determinado número de minutos de longa distância usados. O custo total de cada plano de pagamento pode ser representado por uma função linear. Para resolver o problema, precisaremos comparar as funções. Nesta seção, consideraremos métodos de comparação de funções usando gráficos.

Representação gráfica de funções lineares

Anteriormente, vimos que o gráfico de uma função linear é uma linha reta. Também pudemos ver os pontos da função, bem como o valor inicial de um gráfico. Ao representar graficamente duas funções, podemos comparar mais facilmente suas características. Existem três métodos básicos de representação gráfica de funções lineares:

Faça um gráfico dos pontos e, em seguida, desenhe uma linha através dos pontos.
Use o intercepto y e a inclinação.
Use transformações da função de identidade$f(x)=x$.

Representação gráfica de uma função traçando pontos

Para encontrar pontos de uma função, podemos escolher valores de entrada, avaliar a função com esses valores de entrada e calcular os valores de saída. Os valores de entrada e os valores de saída correspondentes formam pares de coordenadas. Em seguida, traçamos os pares de coordenadas em uma grade. Em geral, devemos avaliar a função com no mínimo duas entradas para encontrar pelo menos dois pontos no gráfico. Por exemplo, dada a função$f(x)=2x$, podemos usar os valores de entrada 1 e 2. Avaliar a função para um valor de entrada de 1 gera um valor de saída de 2, que é representado pelo ponto$(1,2)$. Avaliar a função para um valor de entrada de 2 gera um valor de saída de 4, que é representado pelo ponto$(2,4)$. A escolha de três pontos geralmente é aconselhável porque, se os três pontos não caírem na mesma linha, sabemos que cometemos um erro.

Como fazer: Dada uma função linear, plote graficamente pontos.

Escolha um mínimo de dois valores de entrada.
Avalie a função em cada valor de entrada.
Use os valores de saída resultantes para identificar pares de coordenadas.
Faça um gráfico dos pares de coordenadas em uma grade.
Desenhe uma linha através dos pontos.

Exemplo$\PageIndex{1}$: Graphing by Plotting Points

Faça um gráfico$f(x)=−\frac{2}{3}x+5$ traçando pontos.

Solução

Comece escolhendo os valores de entrada. Essa função inclui uma fração com um denominador de 3, então vamos escolher múltiplos de 3 como valores de entrada. Escolheremos 0, 3 e 6.

Avalie a função em cada valor de entrada e use o valor de saída para identificar pares de coordenadas.

\[\begin{align*} x&=0 & f(0)&=-\dfrac{2}{3}(0)+5=5\rightarrow(0,5) \\ x&=3 & f(3)&=-\dfrac{2}{3}(3)+5=3\rightarrow(3,3) \\ x&=6 & f(6)&=-\dfrac{2}{3}(6)+5=1\rightarrow(6,1) \end{align*}\]

Faça um gráfico dos pares de coordenadas e desenhe uma linha através dos pontos. $\PageIndex{1}$A figura representa o gráfico da função$f(x)=−\frac{2}{3}x+5$.

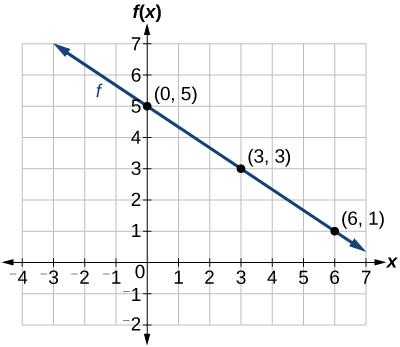
gráfico de f (x) — Figura$\PageIndex{1}$: O gráfico da função linear$f(x)=−\frac{2}{3}x+5$.

Análise

O gráfico da função é uma linha conforme o esperado para uma função linear. Além disso, o gráfico tem uma inclinação descendente, o que indica uma inclinação negativa. Isso também é esperado a partir da taxa de mudança constante negativa na equação da função.

Exercício$\PageIndex{1}$

Faça um gráfico$f(x)=−\frac{3}{4}x+6$ traçando pontos.

Responda: $alt$
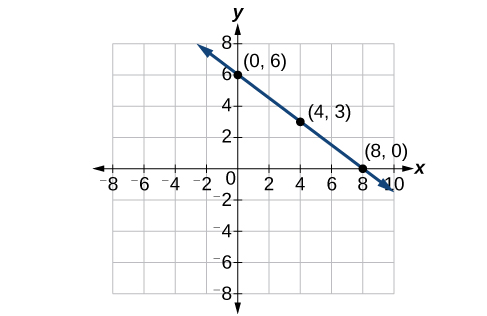
Figura$\PageIndex{2}$

Representação gráfica de uma função usando intercepto y e inclinação

Outra forma de representar graficamente funções lineares é usar características específicas da função em vez de traçar pontos. A primeira característica é seu intercepto y, que é o ponto em que o valor de entrada é zero. Para encontrar o intercepto y, podemos definir$x=0$ a equação.

A outra característica da função linear é sua inclinação$m$, que é uma medida de sua inclinação. Lembre-se de que a inclinação é a taxa de mudança da função. A inclinação de uma função é igual à razão entre a mudança nas saídas e a mudança nas entradas. Outra forma de pensar sobre a inclinação é dividindo a diferença vertical, ou subida, pela diferença horizontal ou corrida. Encontramos o intercepto y e a inclinação em funções lineares.

Vamos considerar a seguinte função.

\[f(x)=\dfrac{1}{2}x+1\]

A inclinação é$\frac{1}{2}$. Como a inclinação é positiva, sabemos que o gráfico se inclinará para cima da esquerda para a direita. O intercepto y é o ponto no gráfico quando$x=0$. O gráfico cruza o eixo y em$(0,1)$. Agora sabemos a inclinação e o intercepto y. Podemos começar a representar graficamente traçando o ponto.$(0,1)$ Sabemos que a inclinação é elevação sobre corrida,$m=\frac{\text{rise}}{\text{run}}$. Do nosso exemplo, temos$m=\frac{1}{2}$, o que significa que o aumento é 1 e a corrida é 2. Então, a partir do nosso intercepto y$(0,1)$, podemos subir 1 e depois executar 2, ou correr 2 e depois subir 1. Repetimos até termos alguns pontos e, em seguida, traçamos uma linha através dos pontos, conforme mostrado na Figura$\PageIndex{3}$.

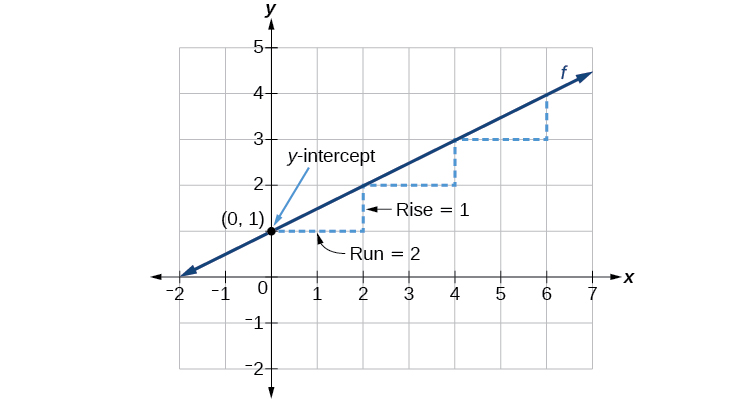
Gráfico de f (x) mostrando inclinação e intercepto y — Figura$\PageIndex{3}$: Gráfico de$f(x)$ exibição da inclinação e do intercepto y

Interpretação gráfica de uma função linear

Na equação$f(x)=mx+b$

$b$é o intercepto y do gráfico e indica o ponto$(0,b)$ em que o gráfico cruza o eixo y.
$m$é a inclinação da linha e indica o deslocamento vertical (subida) e o deslocamento horizontal (corrida) entre cada par sucessivo de pontos. Lembre-se da fórmula para a inclinação:

\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\]

Exercício$\PageIndex{1}$

Todas as funções lineares têm interceptos y?

Responda: Sim. Todas as funções lineares cruzam o eixo y e, portanto, têm interceptos y. (Observação: uma linha vertical paralela ao eixo y não tem um intercepto y, mas não é uma função.)

Como fazer: Dada a equação de uma função linear, represente graficamente a função usando o intercepto y e a inclinação.

Avalie a função em um valor de entrada de zero para encontrar o intercepto y.
Identifique a inclinação como a taxa de variação do valor de entrada.
Faça um gráfico do ponto representado pelo intercepto y.
Use$\frac{\text{rise}}{\text{run}}$ para determinar pelo menos mais dois pontos na linha.
Desenhe a linha que passa pelos pontos.

Exemplo$\PageIndex{2}$: Graphing by Using the y-intercept and Slope

Faça um gráfico$f(x)=−\frac{2}{3}x+5$ usando o intercepto y e a inclinação.

Solução

Avalie a função at$x=0$ para encontrar o intercepto y. O valor de saída quando$x=0$ é 5, então o gráfico cruzará o eixo y em$(0,5)$.

De acordo com a equação da função, a inclinação da linha é$-\frac{2}{3}$. Isso nos diz que para cada diminuição vertical na “elevação” de —2 unidades, a “corrida” aumenta em 3 unidades na direção horizontal. Agora podemos representar graficamente a função traçando primeiro o intercepto y no gráfico da Figura$\PageIndex{4}$. Do valor inicial,$(0,5)$ descemos 2 unidades e para a direita 3 unidades. Podemos estender a linha para a esquerda e para a direita repetindo e, em seguida, desenhar uma linha através dos pontos.

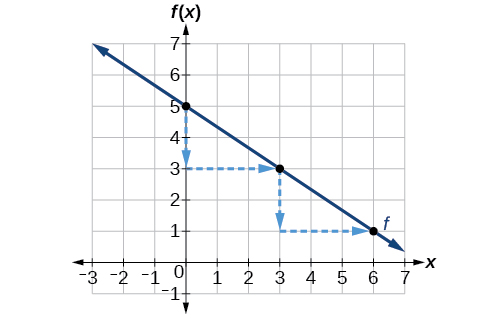
Análise

O gráfico se inclina para baixo da esquerda para a direita, o que significa que ele tem uma inclinação negativa conforme o esperado.

Exercício$\PageIndex{2}$

Encontre um ponto no gráfico que desenhamos no Exemplo$\PageIndex{2}$ que tenha um valor x negativo.

Responda: As respostas possíveis incluem$(−3,7)$$(−6,9)$, ou$(−9,11)$.

Representação gráfica de uma função usando transformações

Outra opção para representar graficamente é usar transformações da função de identidade$f(x)=x$. Uma função pode ser transformada por uma mudança para cima, para baixo, para a esquerda ou para a direita. Uma função também pode ser transformada usando uma reflexão, estiramento ou compressão.

Alongamento ou compressão vertical

Na equação$f(x)=mx$, o$m$ está atuando como o alongamento vertical ou compressão da função de identidade. Quando$m$ é negativo, há também uma reflexão vertical do gráfico. Observe na Figura$\PageIndex{5}$ que multiplicar a equação de$f(x)=x$ por$m$ estica o gráfico de$f$ por um fator de$m$ unidades se$m>1$ e comprime o gráfico de$f$ por um fator de$m$ unidades if$0<m<1$. Isso significa que quanto maior o valor absoluto de$m$, maior a inclinação.

alt — Figura$\PageIndex{5}$: Alongamentos e compressões verticais e reflexos sobre a função$f(x)=x$.

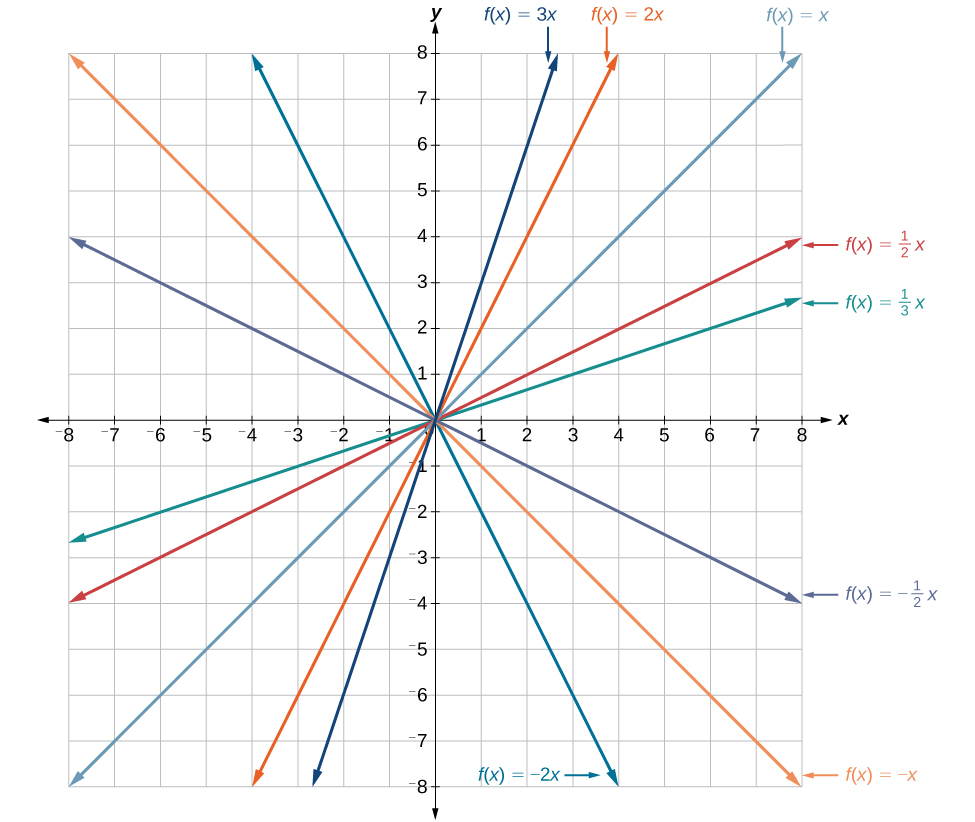
Mudança vertical

No$f(x)=mx+b$, o$b$ atua como o deslocamento vertical, movendo o gráfico para cima e para baixo sem afetar a inclinação da linha. Observe na Figura$\PageIndex{6}$ que adicionar um valor de$b$ à equação de$f(x)=x$ desloca o gráfico de$f$ um total de$b$ unidades para cima se$b$ for positivo e$|b|$ unidades para baixo se$b$ for negativo.

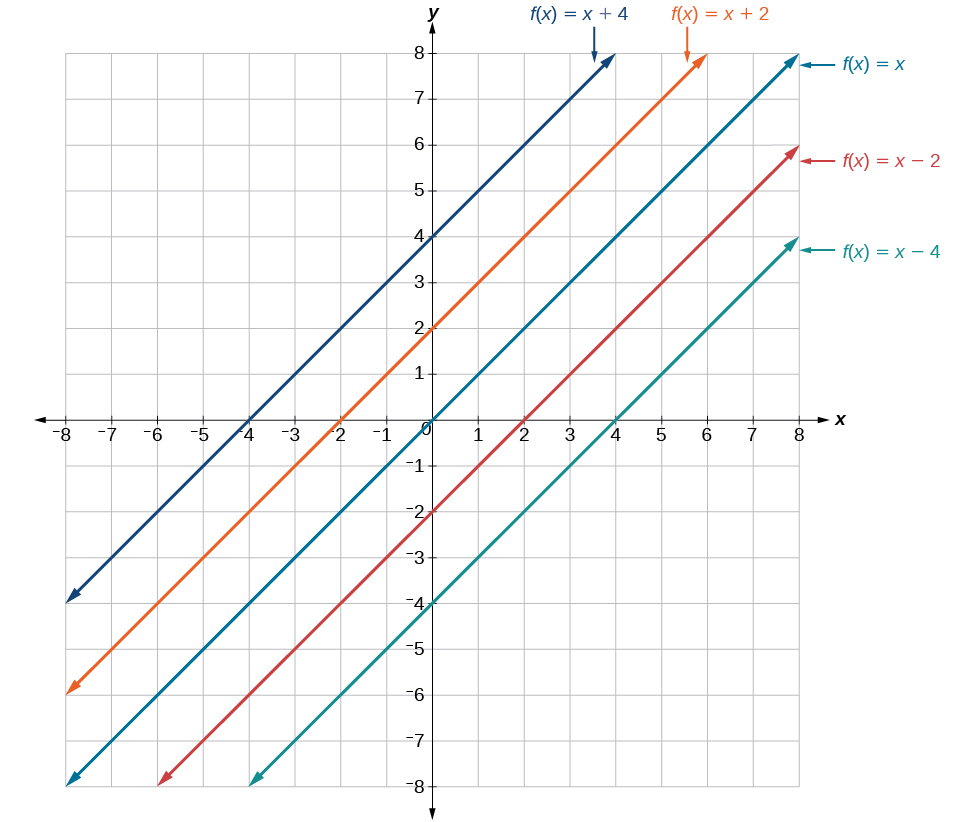
Este gráfico ilustra os deslocamentos verticais da função f (x) =x. — Figura$\PageIndex{6}$: Este gráfico ilustra os deslocamentos verticais da função$f(x)=x$.

Usar alongamentos ou compressões verticais junto com deslocamentos verticais é outra forma de identificar diferentes tipos de funções lineares. Embora essa possa não ser a maneira mais fácil de representar graficamente esse tipo de função, ainda é importante praticar cada método.

$alt$ Dada a equação de uma função linear, use transformações para representar graficamente a função linear no formulário$f(x)=mx+b$.

Gráfico$f(x)=x$.
Estique ou comprima verticalmente o gráfico por um fator$m$.
Desloque o gráfico para cima ou para baixo em$b$ unidades.

Exemplo$\PageIndex{3}$: Graphing by Using Transformations

Gráfico$f(x)=\frac{1}{2}x−3$ usando transformações.

Solução

A equação da função mostra que$m=\frac{1}{2}$, portanto, a função de identidade é comprimida verticalmente por$\frac{1}{2}$. A equação da função também mostra que$b=−3$, portanto, a função de identidade é deslocada verticalmente para baixo em 3 unidades. Primeiro, faça um gráfico da função de identidade e mostre a compressão vertical como na Figura$\PageIndex{7}$.

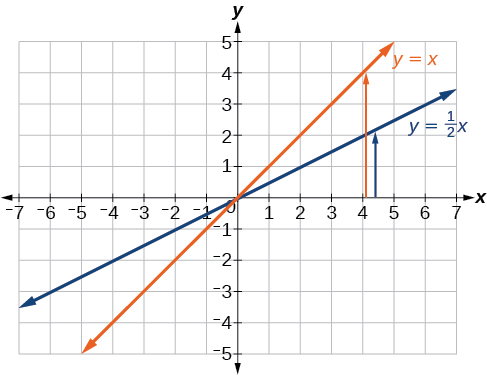
A função, y=x, comprimida por um fator de 1/2. — Figura$\PageIndex{7}$: A função$y=x$, comprimida por um fator de$\frac{1}{2}$.

Em seguida, mostre o deslocamento vertical como na Figura$\PageIndex{8}$.

alt — Figura$\PageIndex{8}$: A função$y=\frac{1}{2}x$, diminuiu 3 unidades.

Exercício$\PageIndex{3}$

Gráfico$f(x)=4+2x$, usando transformações.

Responda: $alt$
Figura$\PageIndex{9}$

$alt$ No Exemplo 2.2.3, poderíamos ter esboçado o gráfico invertendo a ordem das transformações?

Não. A ordem das transformações segue a ordem das operações. Quando a função é avaliada em uma determinada entrada, a saída correspondente é calculada seguindo a ordem das operações. É por isso que realizamos a compressão primeiro. Por exemplo, seguindo a ordem: Deixe a entrada ser 2.

\[\begin{align} f(2)&=\dfrac{1}{2}(2)-3 \\ &=1-3\\ &=-2 \end{align}\]

Escrevendo a equação para uma função a partir do gráfico de uma linha

Lembre-se de que em Funções Lineares, escrevemos a equação para uma função linear a partir de um gráfico. Agora podemos ampliar o que sabemos sobre a representação gráfica de funções lineares para analisar gráficos um pouco mais de perto. Comece dando uma olhada na Figura$\PageIndex{10}$. Podemos ver imediatamente que o gráfico cruza o eixo y no ponto$(0, 4)$, então esse é o intercepto y.

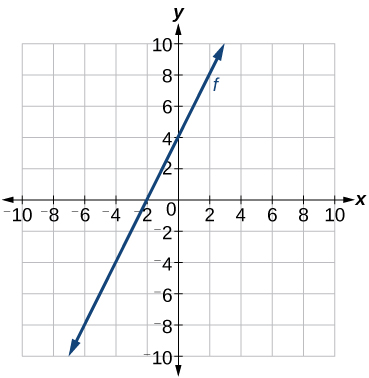
Figura$\PageIndex{10}$: Gráfico de uma função linear

Então, podemos calcular a inclinação encontrando a subida e a corrida. Podemos escolher quaisquer dois pontos, mas vamos dar uma olhada no ponto (−2,0). Para ir desse ponto até o intercepto y, devemos subir 4 unidades (subir) e para a direita 2 unidades (correr). Portanto, a inclinação deve ser

\[m=\dfrac{\text{rise}}{\text{run}}=\dfrac{4}{2}=2\]

Substituir a inclinação e o intercepto y na forma de interceptação de inclinação de uma linha dá

\[y=2x+4\]

$alt$ Dado um gráfico da função linear, encontre a equação para descrever a função.

Identifique o intercepto y de uma equação.
Escolha dois pontos para determinar a inclinação.
Substitua o intercepto y e a inclinação na forma de interceptação de inclinação de uma linha.

Exemplo$\PageIndex{4}$: Matching Linear Functions to Their Graphs

Combine cada equação das funções lineares com uma das linhas na Figura$\PageIndex{11}$.

$f(x)=2x+3$
$g(x)=2x−3$
$h(x)=−2x+3$
$j(x)=\frac{1}{2}x+3$

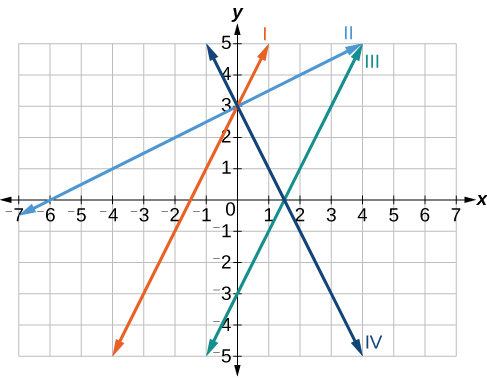
Figura$\PageIndex{11}$: Gráfico de quatro funções lineares

Solução

Analise as informações de cada função.

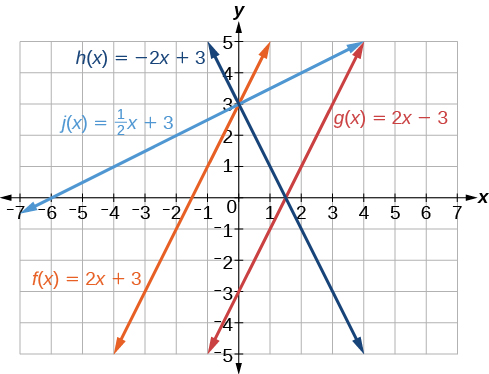
Essa função tem uma inclinação de 2 e um intercepto y de 3. Ele deve passar pelo ponto$(0, 3)$ e inclinar-se para cima da esquerda para a direita. Podemos usar dois pontos para encontrar a inclinação ou compará-la com as outras funções listadas. A função$g$ tem a mesma inclinação, mas um intercepto y diferente. As linhas I e III têm a mesma inclinação porque têm a mesma inclinação. A linha III não passa$(0, 3)$, então$f$ deve ser representada pela linha I.
Essa função também tem uma inclinação de 2, mas um intercepto y de −3. Ele deve passar pelo ponto$(0,−3)$ e inclinar-se para cima da esquerda para a direita. Ele deve ser representado pela linha III.
Essa função tem uma inclinação de —2 e um intercepto y de 3. Essa é a única função listada com uma inclinação negativa, então ela deve ser representada pela linha IV porque ela se inclina para baixo da esquerda para a direita.
Essa função tem uma inclinação de$\frac{1}{2}$ e um intercepto y de 3. Ele deve passar pelo ponto (0, 3) e inclinar-se para cima da esquerda para a direita. As linhas I e II passam$(0, 3)$, mas a inclinação de$j$ é menor que a inclinação de$f$, então a linha para$j$ deve ser mais plana. Essa função é representada pela Linha II.

Agora podemos rotular novamente as linhas como na Figura$\PageIndex{12}$.

Encontrando o intercepto x de uma linha

Até agora, encontramos os interceptos y de uma função: o ponto em que o gráfico da função cruza o eixo y. Uma função também pode ter um intercepto x, que é a coordenada x do ponto em que o gráfico da função cruza o eixo x. Em outras palavras, é o valor de entrada quando o valor de saída é zero.

Para encontrar o intercepto x, defina uma função$f(x)$ igual a zero e resolva o valor de$x$. Por exemplo, considere a função mostrada.

\[f(x)=3x−6\]

Defina a função igual a 0 e resolva para$x$.

\[\begin{align} 0&=3x-6 \\ 6&=3x \\ 2&=x \\ x&=2 \end{align}\]

O gráfico da função cruza o eixo x no ponto$(2, 0)$.

$alt$ Todas as funções lineares têm interceptos x?

Figura$\PageIndex{13}$.

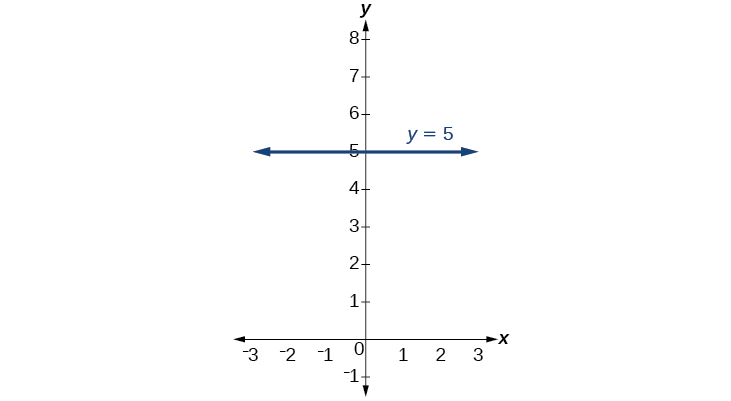
Gráfico de y = 5 — Figura$\PageIndex{13}$: Gráfico de$y= 5$.

Nota: x-intercept

O intercepto x da função é o valor de$x$ quando$f(x)=0$. Isso pode ser resolvido pela equação$0=mx+b$.

Exemplo$\PageIndex{5}$: Finding an x-intercept

Encontre o intercepto x de$f(x)=\frac{1}{2}−3$.

Solução

Defina a função igual a zero para resolver$x$.

\[\begin{align*} 0&=\dfrac{1}{2}x-3 \\ 3&=\dfrac{1}{2}x \\ 6 &= x \\ x&=6 \end{align*}\]

O gráfico cruza o eixo x no ponto$(6, 0)$.

Análise

Um gráfico da função é mostrado na Figura$\PageIndex{14}$. Podemos ver que o intercepto x é o$(6, 0)$ que esperávamos.

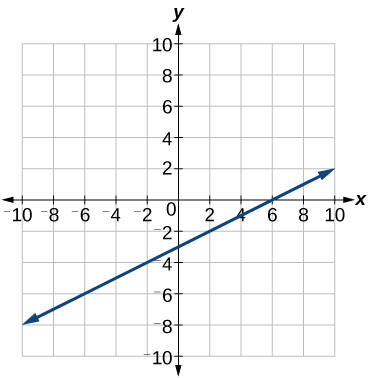
O gráfico da função linear f (x) = (1/2) x-3 — Figura$\PageIndex{14}$: O gráfico da função linear$f(x)=\frac{1}{2}x−3$.

Exercício$\PageIndex{5}$

Encontre o intercepto x de$f(x)=\frac{1}{4}x−4$.

Responda: $(16, 0)$

Descrevendo linhas horizontais e verticais

Há dois casos especiais de linhas em um gráfico: linhas horizontais e verticais. Uma linha horizontal indica uma saída constante, ou valor y. Na Figura$\PageIndex{15}$, vemos que a saída tem um valor de 2 para cada valor de entrada. A mudança nas saídas entre quaisquer dois pontos, portanto, é 0. Na fórmula da inclinação, o numerador é 0, então a inclinação é 0. Se usarmos$m=0$ na equação$f(x)=mx+b$, a equação simplifica para$f(x)=b$. Em outras palavras, o valor da função é uma constante. Esse gráfico representa a função$f(x)=2$.

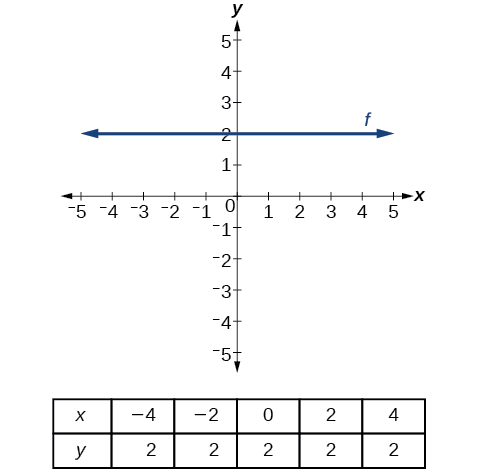
Uma linha horizontal representando a função f (x) =2 — Figura$\PageIndex{15}$: Uma linha horizontal representando a função$f(x)=2$.

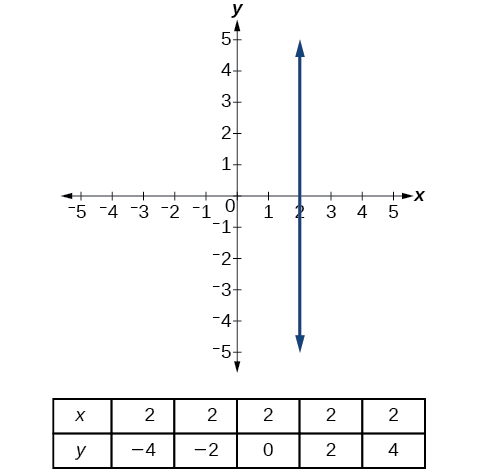
Uma linha vertical indica uma entrada constante, ou valor x. Podemos ver que o valor de entrada para cada ponto na linha é 2, mas o valor de saída varia. Como esse valor de entrada é mapeado para mais de um valor de saída, uma linha vertical não representa uma função. Observe que, entre quaisquer dois pontos, a alteração nos valores de entrada é zero. Na fórmula da inclinação, o denominador será zero, então a inclinação de uma linha vertical é indefinida.

Observe que uma linha vertical, como a da Figura$\PageIndex{17}$, tem um intercepto x, mas nenhum intercepto y, a menos que seja a linha$x=0$. Esse gráfico representa a linha$x=2$.

alt — Figura$\PageIndex{17}$: A linha vertical$x=2$,, que não representa uma função.

Definições: Linhas horizontais e verticais

As linhas podem ser horizontais ou verticais.

Uma linha horizontal é uma linha definida por uma equação no formulário$f(x)=b$.
Uma linha vertical é uma linha definida por uma equação no formulário$x=a$.

Exemplo$\PageIndex{6}$: Writing the Equation of a Horizontal Line

Escreva a equação da linha representada graficamente na Figura$\PageIndex{18}$.

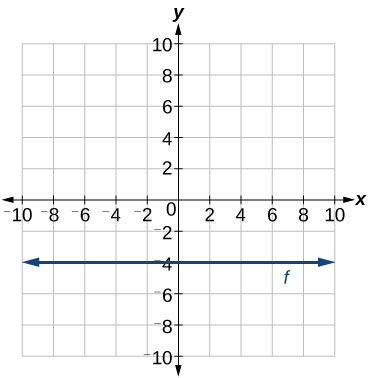
Gráfico de x=7. — Figura$\PageIndex{18}$: Gráfico de$x=7$.

Solução

Para qualquer valor x, o valor y é −4, então a equação é$y=−4$.

Exemplo$\PageIndex{7}$: Writing the Equation of a Vertical Line

Escreva a equação da linha representada graficamente na Figura$\PageIndex{19}$.

Figura$\PageIndex{19}$: Gráfico de uma linha vertical

Solução

O valor x constante é 7, então a equação é$x=7$.

Determinando se as linhas são paralelas ou perpendiculares

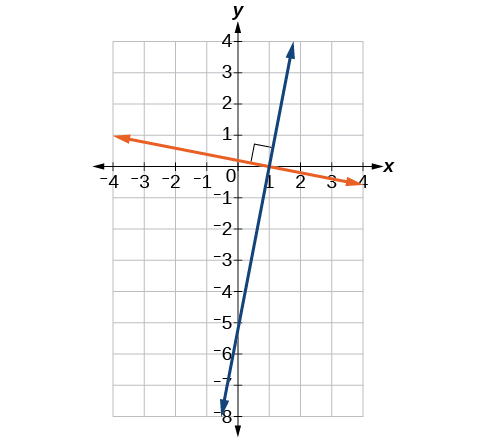
As duas linhas na Figura$\PageIndex{20}$ são linhas paralelas: elas nunca se cruzarão. Observe que eles têm exatamente a mesma inclinação, o que significa que suas inclinações são idênticas. A única diferença entre as duas linhas é o intercepto y. Se mudássemos uma linha verticalmente em direção à interceptação y da outra, elas se tornariam a mesma linha.

Gráfico de duas funções em que a linha azul é y= - (2/3) x + 1 e a linha azul bebê é <span translate= — Figura\ (\ PageIndex {20}\): Linhas paralelas.

Podemos determinar a partir de suas equações se duas retas são paralelas comparando suas inclinações. Se as inclinações forem iguais e as interceptações y forem diferentes, as linhas serão paralelas. Se as inclinações forem diferentes, as linhas não serão paralelas.

alt — $\PageIndex{21}$As figuras são perpendiculares.

Gráfico de duas funções em que a linha azul é perpendicular à linha laranja — Figura$\PageIndex{21}$: Linhas perpendiculares.

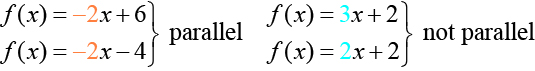
As linhas perpendiculares não têm a mesma inclinação. As inclinações das linhas perpendiculares são diferentes umas das outras de uma maneira específica. A inclinação de uma linha é o inverso negativo da inclinação da outra linha. O produto de um número e seu recíproco é 1. Portanto, se$m_1$ e$m_2$ forem recíprocos negativos um do outro, eles podem ser multiplicados juntos para produzir —1.

\[m_1m_2=−1\]

Para encontrar o inverso de um número, divida 1 pelo número. Portanto, o recíproco de 8 é$\frac{1}{8}$, e o recíproco de$\frac{1}{8}$ é 8. Para encontrar o recíproco negativo, primeiro encontre o recíproco e depois altere o sinal.

Assim como acontece com as retas paralelas, podemos determinar se duas retas são perpendiculares comparando suas inclinações, assumindo que as linhas não são horizontais nem perpendiculares. A inclinação de cada linha abaixo é a recíproca negativa da outra, então as linhas são perpendiculares.

\[\begin{align} f(x)&=\dfrac{1}{4}x+2 &\text{negative reciprocal of $\dfrac{1}{4}$ is -4} \\ f(x)&=-4x+3 &\text{negative reciprocal of -4 is $\dfrac{1}{4}$} \end{align}\]

O produto das encostas é —1.

\[−4\Big(\dfrac{1}{4}\Big)=−1\]

Definições: Linhas paralelas e perpendiculares

Duas retas são linhas paralelas se não se cruzarem. As inclinações das linhas são as mesmas.

$f(x)=m_1x+b_1$e$g(x)=m_2x+b_2$ são paralelos se$m_1 = m_2$.

Se e somente se$b_1=b_2$ e$m_1=m_2$, dizemos que as linhas coincidem. As linhas coincidentes são a mesma linha.

Duas retas são linhas perpendiculares se elas se cruzarem em ângulos retos.

$f(x)=m_1x+b_1$e$g(x)=m_2x+b_2$ são perpendiculares se$m_1m_2=−1$, e assim por diante$m_2=\dfrac{−1}{m_1}$.

Exemplo$\PageIndex{8}$: Identifying Parallel and Perpendicular Lines

Dadas as funções abaixo, identifique as funções cujos gráficos são um par de linhas paralelas e um par de linhas perpendiculares.

\[\begin{align} f(x)&=2x+3 & h(x)&=-2x+2 \\ g(x)&=\dfrac{1}{2}x-4 & f(x)&=2x-6 \end{align}\]

Solução

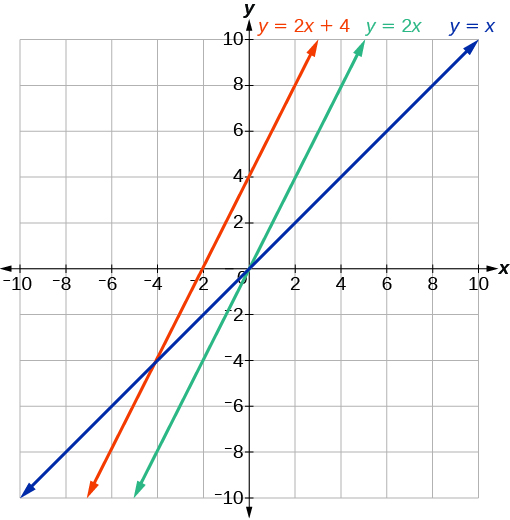
As linhas paralelas têm a mesma inclinação. Como as funções$f(x)=2x+3$ e$j(x)=2x−6$ cada uma têm uma inclinação de 2, elas representam linhas paralelas. As linhas perpendiculares têm inclinações recíprocas negativas. Como −2 e 2$\frac{1}{2}$ são recíprocos negativos, as equações$g(x)=\frac{1}{2}x−4$ e$h(x)=−2x+2$ representam retas perpendiculares.

Análise

Um gráfico das linhas é mostrado na Figura$\PageIndex{22}$.

Gráfico de quatro funções em que a linha azul é h (x) = -2x + 2, a linha laranja é f (x) = 2x + 3, a linha verde é j (x) = 2x - 6 e a linha vermelha é g (x) = 1/2x - 4. — Figura$\PageIndex{22}$: Gráfico de$h(x)$ (azul),$f(x)$ (laranja),$j(x)$ (verde) e$g(x)$ (vermelho)

O gráfico mostra que as linhas$f(x)=2x+3$ e$j(x)=2x–6$ são paralelas, e as linhas$g(x)=\frac{1}{2}x–4$ e$h(x)=−2x+2$ são perpendiculares.

Escrevendo a equação de uma reta paralela ou perpendicular a uma determinada linha

Se soubermos a equação de uma reta, podemos usar o que sabemos sobre inclinação para escrever a equação de uma reta que seja paralela ou perpendicular à linha dada.

Escrevendo equações de retas paralelas

Suponha, por exemplo, que recebamos a seguinte equação.

\[f(x)=3x+1 \nonumber\]

Sabemos que a inclinação da linha formada pela função é 3. Também sabemos que o intercepto y é$(0,1)$. Qualquer outra linha com uma inclinação de 3 será paralela$f(x)$ a. Portanto, as linhas formadas por todas as seguintes funções serão paralelas$f(x)$ a.

\[\begin{align*} g(x)&=3x+6 \\ h(x)&=3x+1\\ p(x)&=3x+\dfrac{2}{3} \end{align*}\]

Suponha que então queiramos escrever a equação de uma linha que é paralela$f$ e passa pelo ponto$(1, 7)$. Já sabemos que a inclinação é 3. Só precisamos determinar qual valor para$b$ fornecerá a linha correta. Podemos começar com a forma ponto-inclinação de uma equação para uma reta e depois reescrevê-la na forma de interceptação de inclinação.

\[\begin{align*} y−y_1&=m(x−x_1) \\ y−7&=3(x−1) \\ y−7&=3x−3 \\ y&=3x+4 \end{align*}\]

Então$g(x)=3x+4$ é paralelo$f(x)=3x+1$ e passa pelo ponto$(1, 7)$.

Como...

Dada a equação de uma função e um ponto pelo qual seu gráfico passa, escreva a equação de uma reta paralela à linha dada que passa pelo ponto dado.

Encontre a inclinação da função.
Substitua os valores fornecidos na equação geral de inclinação do ponto ou na equação de interceptação de inclinação por uma linha.
Simplifique.

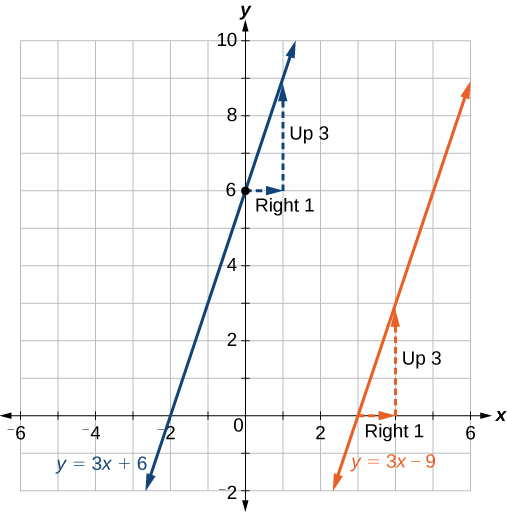
Exemplo$\PageIndex{9}$: Finding a Line Parallel to a Given Line

Encontre uma linha paralela ao gráfico$f(x)=3x+6$ que passa pelo ponto$(3, 0)$.

Solução

A inclinação da linha dada é 3. Se escolhermos a forma de interceptação de inclinação, podemos substituir$m=3$$x=3$, e$f(x)=0$ na forma de interceptação de inclinação para encontrar o intercepto y.

\[\begin{align*} g(x)&=3x+b \\ 0&=3(3)+b \\ b&=-9 \end{align*}\]

A linha paralela à$f(x)$ que passa$(3,0)$ é$g(x)=3x−9$.

Análise

Podemos confirmar que as duas linhas são paralelas representando-as graficamente. A figura$\PageIndex{23}$ mostra que as duas linhas nunca se cruzarão.

Gráfico de duas funções em que a linha azul é y = 3x + 6 e a linha laranja é y = 3x - 9. — Figura$\PageIndex{23}$: Gráfico de duas funções onde a linha azul está$y=3x+6$ e a linha laranja está$y=3x-9$.

Escrevendo equações de retas perpendiculares

Podemos usar um processo muito semelhante para escrever a equação de uma reta perpendicular a uma determinada linha. Em vez de usar a mesma inclinação, no entanto, usamos o recíproco negativo da inclinação dada. Suponha que recebamos a seguinte função:

\[f(x)=2x+4 \nonumber\]

A inclinação da linha é 2 e seu recíproco negativo é$−\frac{1}{2}$. Qualquer função com uma inclinação de$−\frac{1}{2}$ será perpendicular$f(x)$ a. Portanto, as linhas formadas por todas as seguintes funções serão perpendiculares$f(x)$ a.

\[\begin{align*} g(x)&=-\dfrac{1}{2}x+4 \\[4pt] h(x)&=-\dfrac{1}{2}x+2 \\[4pt] p(x)&=-\dfrac{1}{2}x-\dfrac{1}{2} \end{align*}\]

Como antes, podemos restringir nossas escolhas para uma linha perpendicular específica se soubermos que ela passa por um determinado ponto. Suponha que então queiramos escrever a equação de uma reta que seja perpendicular$f(x)$ e passe pelo ponto$(4, 0)$. Já sabemos que a inclinação é$−\frac{1}{2}$. Agora podemos usar o ponto para encontrar o intercepto y substituindo os valores dados na forma de interceptação de inclinação de uma linha e resolvendo por$b$.

\[\begin{align*} g(x)&=mx+b \\[4pt] 0&=-\dfrac{1}{2}(4)+b \\[4pt] 0 & = -2+b\\[4pt] 2&=b \\ b&=2 \end{align*}\]

A equação para a função com uma inclinação de$−\frac{1}{2}$ e um intercepto y de 2 é

\[g(x)=−\dfrac{1}{2}x+2\]

Então$g(x)=−\frac{1}{2}x+2$ é perpendicular$f(x)=2x+4$ e passa pelo ponto$(4, 0)$. Esteja ciente de que as linhas perpendiculares podem não parecer obviamente perpendiculares em uma calculadora gráfica, a menos que usemos o recurso de zoom quadrado.

$alt$ Uma linha horizontal tem uma inclinação de zero e uma linha vertical tem uma inclinação indefinida. Essas duas retas são perpendiculares, mas o produto de suas inclinações não é —1. Esse fato não contradiz a definição de retas perpendiculares?

Não. Para duas funções lineares perpendiculares, o produto de suas inclinações é —1. No entanto, uma linha vertical não é uma função, então a definição não é contradita.

Como fazer...

Dada a equação de uma função e um ponto pelo qual seu gráfico passa, escreva a equação de uma reta perpendicular à linha dada.

Encontre a inclinação da função.
Determine o recíproco negativo da inclinação.
Substitua a nova inclinação e os valores por$x$ e$y$ do par de coordenadas fornecido em$g(x)=mx+b$.
Resolver para$b$.
Escreva a equação para a linha.

Exemplo$\PageIndex{10}$: Finding the Equation of a Perpendicular Line

Encontre a equação de uma reta perpendicular à$f(x)=3x+3$ que passa pelo ponto$(3, 0)$.

Solução

A linha original tem inclinação$m=3$, então a inclinação da linha perpendicular será sua recíproca negativa, ou$−\frac{1}{3}$. Usando essa inclinação e o ponto dado, podemos encontrar a equação para a reta.

\[\begin{align*} g(x)&= \; –\dfrac{1}{3}x+b \\[4pt] 0&= \; –\dfrac{1}{3}(3)+b \\[4pt] 1&=b \\ b&=1 \end{align*}\]

A linha perpendicular à$f(x)$ que passa$(3, 0)$ é$g(x)=−\frac{1}{3}x+1$.

Análise

Um gráfico das duas linhas é mostrado na Figura$\PageIndex{24}$ abaixo.

Gráfico de duas funções em que a linha azul é g (x) = -1/3x + 1 e a linha laranja é <span translate= — Figura$\PageIndex{24}$: Gráfico de duas funções onde a linha azul está$g(x)= -\frac{1}{3}x+1$ e a linha laranja está$f(x)=3x+6$.

Exercício$\PageIndex{5}$

Dada a função$h(x)=2x−4$, escreva uma equação para a linha$(0,0)$ que passa que é

paralelo a$h(x)$
perpendicular a$h(x)$

Responda: $f(x)=2x$$g(x)=−\frac{1}{2}x$

Como...

Dados dois pontos em uma reta e um terceiro ponto, escreva a equação da reta perpendicular que passa pelo ponto.

Determine a inclinação da linha que passa pelos pontos.
Encontre o recíproco negativo da inclinação.
Use a forma de interceptação de inclinação ou a forma de inclinação de ponto para escrever a equação substituindo os valores conhecidos.
Simplifique.

Exemplo$\PageIndex{11}$: Finding the Equation of a Line Perpendicular to a Given Line Passing through a Point

Uma linha passa pelos pontos$(−2, 6)$$(4,5)$ e. Encontre a equação de uma reta perpendicular que passa pelo ponto$(4,5)$.

A partir dos dois pontos da linha dada, podemos calcular a inclinação dessa linha.

\[\begin{align*} m_1&=\dfrac{5-6}{4−(−2)} \\ &=\dfrac{-1}{6} \\ &=−\dfrac{1}{6} \end{align*}\]

Encontre o recíproco negativo da inclinação.

\[\begin{align*} m_2&=\dfrac{-1}{-\dfrac{1}{6}} \\ &=−1\Big(−\dfrac{6}{1}\Big) \\ & =6 \end{align*}\]

Podemos então resolver o intercepto y da linha que passa pelo ponto$(4,5)$.

\[\begin{align*} g(x)&=6x+b \\ 5&=6(4)+b \\ 5&=24+b \\ −19&=b \\ b&=−19 \end{align*}\]

A equação para a reta que é perpendicular à linha que passa pelos dois pontos dados e também passa pelo ponto$(4,5)$ é

\[y=6x−19 \nonumber\]

Exercício$\PageIndex{1}$

Uma linha passa pelos pontos,$(−2,−15)$$(2,−3)$ e. Encontre a equação de uma reta perpendicular que passa pelo ponto,$(6,4)$.

Responda: $y= \; –\dfrac{1}{3}x+6$

Resolvendo um sistema de equações lineares usando um gráfico

Um sistema de equações lineares inclui duas ou mais equações lineares. Os gráficos de duas linhas se cruzarão em um único ponto se não estiverem paralelos. Duas retas paralelas também podem se cruzar se forem coincidentes, o que significa que elas são a mesma linha e se cruzam em todos os pontos. Para duas linhas que não são paralelas, o único ponto de interseção satisfará ambas as equações e, portanto, representará a solução para o sistema.

Para encontrar esse ponto em que as equações são dadas como funções, podemos resolver um valor de entrada para que$f(x)=g(x)$. Em outras palavras, podemos definir as fórmulas para as linhas iguais uma à outra e resolver a entrada que satisfaz a equação.

Exemplo$\PageIndex{12}$: Finding a Point of Intersection Algebraically

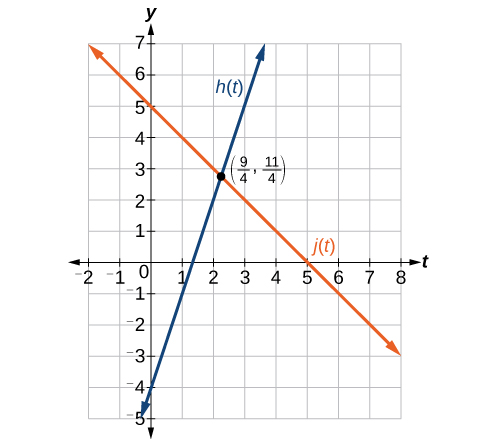
Encontre o ponto de interseção das linhas$h(t)=3t−4$$j(t)=5−t$ e.

Solução

Conjunto$h(t)=j(t)$.

\[\begin{align} 3t-4&=5-t \\ 4t&=9 \\ t&=\dfrac{9}{4} \end{align}\]

Isso nos diz que as linhas se cruzam quando a entrada é$\frac{9}{4}$.

Podemos então encontrar o valor de saída do ponto de interseção avaliando qualquer uma das funções nessa entrada.

\[\begin{align} j\Big( \dfrac{9}{4} \Big)&=5-\dfrac{9}{4} \\ &= \dfrac{11}{4}\end{align}\]

Essas linhas se cruzam no ponto$\Big(\frac{9}{4},\frac{11}{4}\Big)$.

Análise

Olhando para a Figura$\PageIndex{25}$, esse resultado parece razoável.

Gráfico de duas funções h (t) = 3t - 4 e j (t) =t+5 e sua interseção em (9/4, 11/4). — Figura$\PageIndex{25}$: Gráfico de duas funções$h(t) = 3t - 4$$j(t)=t +5$ e sua interseção em$(\frac{9}{4},\frac{11}{4})$.

$alt$ Se nos pedissem que encontrássemos o ponto de interseção de duas linhas paralelas distintas, algo no processo de solução deveria nos alertar para o fato de que não há soluções?

Sim. Depois de definir as duas equações iguais uma à outra, o resultado seria a contradição “$0 = \text{non-zero real number}$”.

Exercício$\PageIndex{7}$

Veja o gráfico na Figura$\PageIndex{23}$ e identifique o seguinte para a função$j(t):$

intercepção y
intercepto (s) x
inclinação
É$j(t)$ paralelo ou perpendicular a$h(t)$ (ou nenhum dos dois)?
É$j(t)$ uma função crescente ou decrescente (ou nenhuma)?
Escreva uma descrição da transformação para a$j(t)$ partir da função do kit de ferramentas de identidade$f(x)=x$.

Responda

$(0,5)$
(5, 0)
Inclinação -1
Nem paralelo nem perpendicular
Função decrescente
Dada a função de identidade, execute um giro vertical (sobre o eixo t) e suba 5 unidades.

Exemplo$\PageIndex{13}$: Finding a Break-Even Point

Uma empresa vende capacetes esportivos. A empresa incorre em um custo fixo único de $250.000. Cada capacete custa $120 para ser produzido e é vendido por $140.

Encontre a função de custo$C$,, para produzir$x$ capacetes, em dólares.
Encontre a função de receita$R$,, da venda de$x$ capacetes, em dólares.
Encontre o ponto de equilíbrio, o ponto de interseção dos dois gráficos$C$$R$ e.

Solução

a. A função de custo é a soma do custo fixo, $125.000, e o custo variável, $120 por capacete.

$C(x)=120x+250,000$

b. A função de receita é a receita total da venda de$x$ capacetes,$R(x)=140x$.

c. O ponto de equilíbrio é o ponto de interseção do gráfico das funções de custo e receita. Para encontrar a coordenada x do par de coordenadas do ponto de interseção, defina as duas equações iguais e resolva para$x$.

\[\begin{align*} C(x)&=R(x) \\ 250,000+120x&=140x \\ 250,000&=20x \\ x&=12,500 \end{align*}\]

Para encontrar$y$, avalie a receita ou a função de custo em 12.500.

\[\begin{align*} R(20)&=140(12,500) \\ &=$1,750,000 \end{align*}\]

O ponto de equilíbrio é$(12,500,1,750,000)$.

Análise

Isso significa que, se a empresa vender 12.500 capacetes, eles se equilibram; tanto as vendas quanto os custos incorridos equivalem a 1,75 milhão de dólares. Veja a Figura$\PageIndex{26}$.

Gráfico das duas funções, C (x) e R (x), onde mostra que abaixo (12500, 1750000) a empresa perde dinheiro e acima desse ponto a empresa obtém lucro. — Figura$\PageIndex{26}$: Gráfico das duas funções,$C(x)$ e$R(x)$ onde mostra que abaixo$(12500, 1750000)$ a empresa perde dinheiro e acima desse ponto a empresa obtém lucro.

Conceitos-chave

As funções lineares podem ser representadas graficamente traçando pontos ou usando o intercepto y e a inclinação.
Gráficos de funções lineares podem ser transformados usando deslocamentos para cima, para baixo, para a esquerda ou para a direita, bem como por meio de alongamentos, compressões e reflexões.
O intercepto y e a inclinação de uma linha podem ser usados para escrever a equação de uma linha.
O intercepto x é o ponto em que o gráfico de uma função linear cruza o eixo x.
As linhas horizontais são escritas na forma,$f(x)=b$.
As linhas verticais são escritas na forma,$x=b$.
As linhas paralelas têm a mesma inclinação.
As linhas perpendiculares têm inclinações recíprocas negativas, assumindo que nenhuma delas é vertical.
Uma linha paralela a outra linha, passando por um determinado ponto, pode ser encontrada substituindo o valor da inclinação da linha e os valores x e y do ponto dado na equação e usando$b$ os resultados.$f(x)=mx+b$ Da mesma forma, a forma de inclinação pontual de uma equação também pode ser usada.
Uma reta perpendicular a outra linha, passando por um determinado ponto, pode ser encontrada da mesma maneira, com exceção do uso da inclinação recíproca negativa.
Um sistema de equações lineares pode ser resolvido definindo as duas equações iguais uma à outra e resolvendo para$x$. O valor y pode ser encontrado avaliando qualquer uma das equações originais usando esse valor x.
Um sistema de equações lineares também pode ser resolvido encontrando o ponto de interseção em um gráfico.

Glossário

linha horizontal
uma linha definida por$f(x)=b$, onde$b$ é um número real. A inclinação de uma linha horizontal é 0.

linhas paralelas
duas ou mais linhas com a mesma inclinação

linhas perpendiculares:
duas retas que se cruzam em ângulos retos e têm inclinações que são recíprocas negativas uma da outra.

linha vertical
uma linha definida por$x=a$, onde a é um número real. A inclinação de uma linha vertical é indefinida.

x-intercepta
o ponto no gráfico de uma função linear quando o valor de saída é 0; o ponto no qual o gráfico cruza o eixo horizontal