2.1: Funções lineares
- Page ID
- 189301
- Represente uma função linear.
- Determine se uma função linear está aumentando, diminuindo ou constante.
- Interprete a inclinação como uma taxa de mudança.
- Escreva e interprete uma equação para uma função linear.
- Grafe funções lineares.
- Determine se as linhas são paralelas ou perpendiculares.
- Escreva a equação de uma reta paralela ou perpendicular a uma determinada linha.
Assim como no crescimento de uma planta de bambu, existem muitas situações que envolvem mudanças constantes ao longo do tempo. Considere, por exemplo, o primeiro trem maglev comercial do mundo, o trem MagLev de Xangai (trem maglev do mundo), o trem MagLev de Xangai (Figura\(\PageIndex{1}\)). Ele transporta passageiros confortavelmente por uma viagem de 30 quilômetros do aeroporto até a estação de metrô em apenas oito minutos.
Suponha que um trem maglev percorra uma longa distância e que o trem mantenha uma velocidade constante de 83 metros por segundo por um período de tempo, uma vez que esteja a 250 metros da estação. Como podemos analisar a distância do trem da estação em função do tempo? Nesta seção, investigaremos um tipo de função que é útil para esse propósito e a usaremos para investigar situações do mundo real, como a distância do trem da estação em um determinado momento. O trem maglev deveria percorrer uma longa distância e que o trem mantém uma velocidade constante de 83 metros por segundo por um período de tempo, uma vez que esteja a 250 metros da estação. Como podemos analisar a distância do trem da estação em função do tempo? Nesta seção, investigaremos um tipo de função que é útil para esse propósito e a usaremos para investigar situações do mundo real, como a distância do trem da estação em um determinado momento.
Representando funções lineares
A função que descreve o movimento do trem é uma função linear, que é definida como uma função com uma taxa de variação constante, ou seja, um polinômio de grau 1. Há várias maneiras de representar uma função linear, incluindo forma de palavra, notação de função, forma tabular e forma gráfica. Descreveremos o movimento do trem como uma função usando cada método.
Representando uma função linear em formato de palavra
Vamos começar descrevendo a função linear em palavras. Para o problema do trem que acabamos de considerar, a seguinte frase de palavras pode ser usada para descrever a relação da função.
- A distância do trem da estação é uma função do tempo durante o qual o trem se move a uma velocidade constante mais sua distância original da estação quando começou a se mover em velocidade constante.
A velocidade é a taxa de mudança. Lembre-se de que uma taxa de mudança é uma medida da rapidez com que a variável dependente muda em relação à variável independente. A taxa de variação desse exemplo é constante, o que significa que é a mesma para cada valor de entrada. Conforme o tempo (entrada) aumenta em 1 segundo, a distância correspondente (saída) aumenta em 83 metros. O trem começou a se mover nessa velocidade constante a uma distância de 250 metros da estação.
Representando uma função linear em notação de função
Outra abordagem para representar funções lineares é usar a notação de função. Um exemplo de notação de função é uma equação escrita na forma conhecida como forma de interceptação de inclinação de uma linha, onde x é o valor de entrada,\(m\) é a taxa de variação e\(b\) é o valor inicial da variável dependente.
\[\begin{align*} &\text{Equation form } &y=mx+b \\[4pt] &\text{Equation notation } &f(x)=mx+b \end{align*}\]
No exemplo do trem, podemos usar a notação\(D(t)\) na qual a distância total\(D\) é uma função do tempo\(t\). A taxa,\(m\), é de 83 metros por segundo. O valor inicial da variável dependente\(b\) é a distância original da estação, 250 metros. Podemos escrever uma equação generalizada para representar o movimento do trem.
\[D(t)=83t+250\]
Representando uma função linear em forma tabular
Um terceiro método de representação de uma função linear é por meio do uso de uma tabela. A relação entre a distância da estação e o tempo é representada na Figura\(\PageIndex{2}\). Na tabela, podemos ver que a distância muda em 83 metros a cada aumento de 1 segundo no tempo.
Não. A entrada representa o tempo, portanto, embora números racionais e irracionais não negativos sejam possíveis, números reais negativos não são possíveis neste exemplo. A entrada consiste em números reais não negativos.
Representando uma função linear em formato gráfico
Outra forma de representar funções lineares é visualmente usando um gráfico. Podemos usar a relação de função acima,\(D(t)=83t+250\), para desenhar um gráfico, representado na Figura\(\PageIndex{3}\). Observe que o gráfico é uma linha. Quando traçamos uma função linear, o gráfico é sempre uma linha.
A taxa de mudança, que é constante, determina a inclinação ou inclinação da linha. O ponto em que o valor de entrada é zero é o intercepto vertical, ou intercepto y, da linha. Podemos ver no gráfico da Figura\(\PageIndex{3}\) que o intercepto y no exemplo de trem que acabamos de ver é\((0,250)\) e representa a distância do trem da estação quando ele começou a se mover a uma velocidade constante.
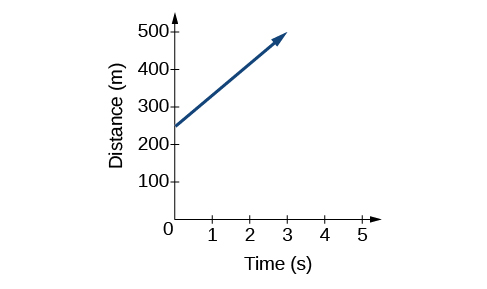
Observe que o gráfico do exemplo do trem é restrito, mas nem sempre é o caso. Considere o gráfico da linha\(f(x)=2x+1\). Pergunte a si mesmo quais números podem ser inseridos na função, ou seja, qual é o domínio da função? O domínio é composto por todos os números reais porque qualquer número pode ser duplicado e, em seguida, adicionar um ao produto.
Uma função linear é uma função cujo gráfico é uma linha. As funções lineares podem ser escritas na forma de interceptação de inclinação de uma linha
\[f(x)=mx+b\]
onde\(b\) é o valor inicial ou inicial da função (quando inserido,\(x=0\)) e\(m\) é a taxa constante de mudança ou inclinação da função. O intercepto y está em\((0,b)\).
A pressão,\(P\), em libras por polegada quadrada (PSI) no mergulhador na Figura\(\PageIndex{4}\) depende de sua profundidade abaixo da superfície da água,\(d\), em pés. Essa relação pode ser modelada pela equação,\(P(d)=0.434d+14.696\). Reafirme essa função em palavras.
Para reafirmar a função em palavras, precisamos descrever cada parte da equação. A pressão em função da profundidade é igual a quatrocentos e trinta e quatro milésimos de profundidade mais quatorze e seiscentos e noventa e seis milésimos.
Análise
O valor inicial, 14.696, é a pressão em PSI no mergulhador a uma profundidade de 0 pés, que é a superfície da água. A taxa de mudança, ou inclinação, é de 0,434 PSI por pé. Isso nos diz que a pressão sobre o mergulhador aumenta 0,434 PSI para cada pé em que sua profundidade aumenta.
Determinando se uma função linear está aumentando, diminuindo ou constante
As funções lineares que usamos nos dois exemplos anteriores aumentaram com o tempo, mas nem todas as funções lineares aumentam. Uma função linear pode ser crescente, decrescente ou constante. Para uma função crescente, como no exemplo do trem, os valores de saída aumentam à medida que os valores de entrada aumentam. O gráfico de uma função crescente tem uma inclinação positiva. Uma linha com uma inclinação positiva se inclina para cima da esquerda para a direita, como na Figura\(\PageIndex{5}\) (a). Para uma função decrescente, a inclinação é negativa. Os valores de saída diminuem à medida que os valores de entrada aumentam. Uma linha com uma inclinação negativa se inclina para baixo da esquerda para a direita, como na Figura\(\PageIndex{5}\) (b). Se a função for constante, os valores de saída serão os mesmos para todos os valores de entrada, então a inclinação é zero. Uma linha com inclinação zero é horizontal, como na Figura\(\PageIndex{5}\) (c).
![Três gráficos representando uma função crescente, uma função decrescente e uma função constante.] Funções de aumento e diminuição](https://math.libretexts.org/@api/deki/files/1061/CNX_Precalc_Figure_02_01_004abc.jpg)
Funções de aumento e diminuição
Funções de aumento e diminuição
A inclinação determina se a função é uma função linear crescente, uma função linear decrescente ou uma função constante.
- \(f(x)=mx+b\)é uma função crescente se\(m>0\).
- \(f(x)=mx+b\)é uma função decrescente se\(m<0\).
- \(f(x)=mx+b\)é uma função constante se\(m=0\).
Alguns estudos recentes sugerem que um adolescente envia em média 60 textos por dia. Para cada um dos cenários a seguir, encontre a função linear que descreve a relação entre o valor de entrada e o valor de saída. Em seguida, determine se o gráfico da função está aumentando, diminuindo ou constante.
- O número total de mensagens de texto que um adolescente envia é considerado uma função do tempo em dias. A entrada é o número de dias e a saída é o número total de textos enviados.
- Um adolescente tem um limite de 500 textos por mês em seu plano de dados. A entrada é o número de dias e a saída é o número total de textos restantes para o mês.
- Um adolescente tem um número ilimitado de textos em seu plano de dados por um custo de $50 por mês. A entrada é o número de dias e a saída é o custo total das mensagens de texto a cada mês.
Solução
Analise cada função.
- A função pode ser representada como\(f(x)=60x\) onde\(x\) está o número de dias. A inclinação, 60, é positiva, então a função está aumentando. Isso faz sentido porque o número total de textos aumenta a cada dia.
- A função pode ser representada como\(f(x)=500−60x\) onde\(x\) está o número de dias. Nesse caso, a inclinação é negativa, então a função está diminuindo. Isso faz sentido porque o número de textos restantes diminui a cada dia e essa função representa o número de textos restantes no plano de dados após\(x\) dias.
- A função de custo pode ser representada\(f(x)=50\) porque o número de dias não afeta o custo total. A inclinação é 0, então a função é constante.
Calculando e interpretando a inclinação
Nos exemplos que vimos até agora, tivemos a inclinação fornecida para nós. No entanto, muitas vezes precisamos calcular a inclinação dados os valores de entrada e saída. Dados dois valores para a entrada\(x_1\) e\(x_2\) dois valores correspondentes para a saída,\(y_1\) e\(y_2\) —que podem ser representados por um conjunto de pontos,\((x_1,y_1)\) e\((x_2,y_2)\) —podemos calcular a inclinação\(m\), da seguinte forma
\[\begin{align*} m &= \dfrac{\text{change in output (rise)}}{ \text{change in input (run)}} \\[4pt] &= \dfrac{{\Delta}y}{ {\Delta}x} = \dfrac{y_2−y_1}{x_2−x_1} \end{align*}\]
onde\({\Delta}y\) está o deslocamento vertical e\({\Delta}x\) é o deslocamento horizontal. Observe na notação da função dois valores correspondentes para a saída\(y_1\) e\(y_2\) para a função\(y_1=f(x_1)\) e\(f\), portanto\(y_2=f(x_2)\), poderíamos escrever de forma equivalente
\[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1} \nonumber\]
A figura\(\PageIndex{6}\) indica como a inclinação da linha entre os pontos,\((x_1,y_1)\) e\((x_2,y_2)\), é calculada. Lembre-se de que a inclinação mede a inclinação. Quanto maior o valor absoluto da inclinação, mais íngreme é a linha.
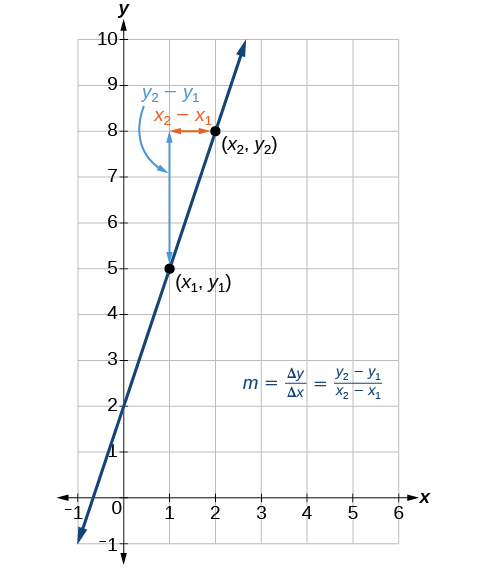
As unidades de inclinação estão sempre\(\frac{\text{units for the output}}{ \text{units for the input}}\)?
Sim. Pense nas unidades como a mudança do valor de saída para cada unidade de mudança no valor de entrada. Um exemplo de inclinação pode ser milhas por hora ou dólares por dia. Observe que as unidades aparecem como uma proporção de unidades para a saída por unidades para a entrada.
A inclinação, ou taxa de variação, de uma função\(m\) pode ser calculada de acordo com o seguinte:
\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\]
onde\(x_1\) e\(x_2\) são valores de entrada\(y_1\) e\(y_2\) são valores de saída.
Dados dois pontos de uma função linear, calcule e interprete a inclinação.
- Determine as unidades para valores de saída e entrada.
- Calcule a alteração dos valores de saída e a alteração dos valores de entrada.
- Interprete a inclinação como a mudança nos valores de saída por unidade do valor de entrada.
Se\(f(x)\) for uma função linear e\((3,−2)\) e\((8,1)\) forem pontos na linha, determine a inclinação. Essa função está aumentando ou diminuindo?
Solução
Os pares de coordenadas são\((3,−2)\)\((8,1)\) e. Para encontrar a taxa de variação, dividimos a mudança na saída pela mudança na entrada.
\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{1-(-2)}{8-3}=\dfrac{3}{5}\]
Também poderíamos escrever a inclinação como\(m=0.6\). A função está aumentando porque\(m>0\).
Análise
Conforme observado anteriormente, a ordem em que escrevemos os pontos não importa quando calculamos a inclinação da linha, desde que o primeiro valor de saída, ou coordenada y, usado corresponda ao primeiro valor de entrada, ou coordenada x, usado.
Se\(f(x)\) for uma função linear e\((2, 3)\) e\((0,4)\) forem pontos na linha, determine a inclinação. Essa função está aumentando ou diminuindo?
- Resposta
-
\(m=\frac{4−3}{0−2} =\frac{1}{-2}=-\frac{1}{2}\); diminuindo porque\(m<0\).
A população de uma cidade aumentou de 23.400 para 27.800 entre 2008 e 2012. Encontre a mudança da população por ano se assumirmos que a mudança foi constante de 2008 a 2012.
A taxa de mudança relaciona a mudança na população com a mudança no tempo. A população aumentou em\(27,800−23,400=4400\) pessoas no intervalo de quatro anos. Para encontrar a taxa de mudança, divida a mudança no número de pessoas pelo número de anos.
\[\dfrac{4,400 \text{ people}}{4 \text{ years}} =1,100 \dfrac{\text{people}}{\text{year}}\]
Assim, a população aumentou em 1.100 pessoas por ano.
Análise
Como nos dizem que a população aumentou, esperaríamos que a inclinação fosse positiva. Essa inclinação positiva que calculamos é, portanto, razoável.
A população de uma pequena cidade aumentou de 1.442 para 1.868 entre 2009 e 2012. Encontre a mudança da população por ano se assumirmos que a mudança foi constante de 2009 a 2012.
- Resposta
-
\(m=\frac{1,868−1,442}{2,012−2,009} = \frac{426}{3} =\text{ 142 people per year}\)
Escrevendo a forma ponto-inclinação de uma equação linear
Até agora, usamos a forma de interceptação de inclinação de uma equação linear para descrever funções lineares. Aqui, aprenderemos outra maneira de escrever uma função linear, a forma ponto-inclinação.
\[y-y_1=m(x-x_1)\]
A forma de inclinação do ponto é derivada da fórmula da inclinação.
\[ \begin{align*} &m=\dfrac{y-y_1}{x-x_1} &\text{assuming }x{\neq}x_1 \\ &m(x-x_1)=\dfrac{y-y_1}{x-x_1}(x-x_1) &\text{Multiply both sides by }(x-x_1). \\ &m(x-x_1)=y-y_1 &\text{Simplify} \\ &y-y_1=m(x-x_1) &\text{Rearrange} \end{align*}\]
Lembre-se de que a forma de interceptação de inclinação e a forma de inclinação de ponto podem ser usadas para descrever a mesma função. Podemos passar de uma forma para outra usando álgebra básica. Por exemplo, suponha que recebamos uma equação na forma de ponto de inclinação,\(y−4=− \frac{1}{2}(x−6)\). Podemos convertê-lo para a forma de interceptação de inclinação, conforme mostrado.
\[\begin{align*} y-4&=-\dfrac{1}{2}(x-6) \\ y-4&=-\dfrac{1}{2}x+3 &\text{Distribute the }-\dfrac{1}{2}. \\ y&=-\dfrac{1}{2}x+7 &\text{Add 4 to each side.}\end{align*}\]
Portanto, a mesma linha pode ser descrita na forma de interceptação de inclinação como\(y=\dfrac{1}{2}x+7\).
A forma de inclinação pontual de uma equação linear assume a forma
\[y-y_1=m(x−x_1)\]
onde\(m\) é a inclinação\(x_1\) e\(y_1\) são as\(y\) coordenadas\(x\) e de um ponto específico pelo qual a linha passa.
Escrevendo a equação de uma reta usando um ponto e a inclinação
A forma ponto-inclinação é particularmente útil se conhecermos um ponto e a inclinação de uma linha. Suponha, por exemplo, que nos digam que uma linha tem uma inclinação de 2 e passa pelo ponto\((4,1)\). Sabemos disso\(m=2\) e daquilo\(x_1=4\)\(y_1=1\) e. Podemos substituir esses valores na equação geral de inclinação do ponto.
\[\begin{align*} y−y_1&=m(x−x_1) \\ y−1&=2(x−4) \end{align*}\]
Se quisermos então reescrever a equação na forma de interceptação de inclinação, aplicamos técnicas algébricas.
\[\begin{align*} y−1&=2(x−4) \\ y−1&=2x−8 &\text{Distribute the 2.} \\ y&=2x−7 &\text{Add 1 to each side.} \end{align*}\]
Ambas as equações\(y−1=2(x−4)\) e\(y=2x–7\), descrevem a mesma linha. Veja a Figura\(\PageIndex{7}\).
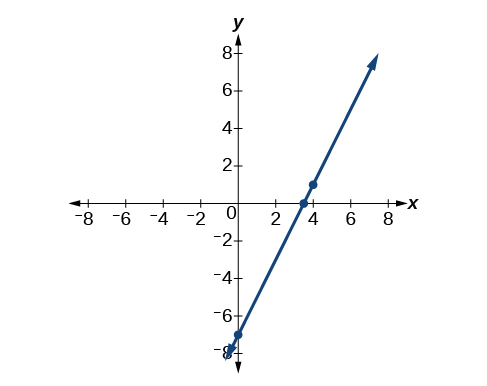
Escreva a forma de inclinação pontual de uma equação de uma reta com uma inclinação de 3 que passa pelo ponto\((6,–1)\). Em seguida, reescreva-o na forma de interceptação de inclinação.
Solução
Vamos descobrir o que sabemos a partir das informações fornecidas. A inclinação é 3, então\(m=3\). Também sabemos um ponto, então sabemos\(x_1=6\)\(y_1 =−1\) e. Agora podemos substituir esses valores na equação geral de inclinação do ponto.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y−(−1)&=3(x−6) &\text{Substitute known values.} \\ y+1&=3(x−6) &\text{Distribute −1 to find point-slope form.} \end{align*}\]
Em seguida, usamos álgebra para encontrar a forma de interceptação de inclinação.
\[\begin{align*} y+1&=3(x−6) \\ y+1&=3x−18 &\text{Distribute 3.} \\ y&=3x−19 &\text{Simplify to slope-intercept form.} \end{align*}\]
Escreva a forma de inclinação pontual de uma equação de uma reta com uma inclinação de —2 que passa pelo ponto\((–2, 2)\). Em seguida, reescreva-o na forma de interceptação de inclinação.
- Resposta
-
\(y−2=−2(x+2)\);\(y=−2x−2\)
Escrevendo a equação de uma linha usando dois pontos
A forma de inclinação pontual de uma equação também é útil se soubermos quaisquer dois pontos pelos quais uma linha passa. Suponha, por exemplo, que saibamos que uma linha passa pelos pontos\((0, 1)\)\((3, 2)\) e. Podemos usar as coordenadas dos dois pontos para encontrar a inclinação.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{2-1}{3-0} \\ &=\dfrac{1}{3} \end{align*}\]
Agora podemos usar a inclinação que encontramos e as coordenadas de um dos pontos para encontrar a equação da reta. Vamos usar\((0,1)\) para o nosso ponto de vista.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=\dfrac{1}{3}(x-0) \end{align*}\]
Como antes, podemos usar álgebra para reescrever a equação na forma de interceptação de inclinação.
\[\begin{align*} y-1&=\dfrac{1}{3}(x-0) \\ y-1&=\dfrac{1}{3}x &\text{Distribute the }\dfrac{1}{3}. \\ y&=\dfrac{1}{3}x+1 &\text{Add 1 to each side.} \end{align*}\]
Ambas as equações descrevem a linha mostrada na Figura\(\PageIndex{8}\).
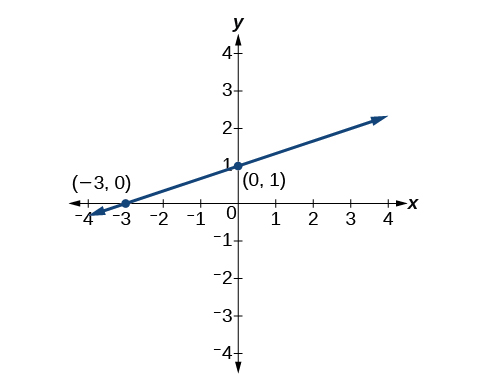
Escreva a forma de inclinação pontual de uma equação de uma reta que passa pelos pontos\((5,1)\)\((8, 7)\) e. Em seguida, reescreva-o na forma de interceptação de inclinação.
Vamos começar encontrando a inclinação.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{7-1}{8-5} \\ &=\dfrac{6}{3} \\ &= 2 \end{align*}\]
Então\(m=2\). Em seguida, substituímos a inclinação e as coordenadas por um dos pontos na equação geral da inclinação do ponto. Podemos escolher qualquer um dos pontos, mas usaremos\((5,1)\).
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=2(x-5) \end{align*}\]
A equação ponto-inclinação da linha é\(y_2–1=2(x_2–5)\). Para reescrever a equação na forma de interceptação de inclinação, usamos álgebra.
\[\begin{align*} y-1&=2(x-5) \\ y-1&=2x-10 \\ y&=2x-9 \end{align*}\]
A equação de interceptação de inclinação da linha é\(y=2x–9\).
\(\PageIndex{4}\): Escreva a forma de inclinação pontual de uma equação de uma reta que passa pelos pontos\((–1,3)\)\((0,0)\) e. Em seguida, reescreva-o na forma de interceptação de inclinação.
Solução
\(y−0=−3(x−0)\);\(y=−3x\)
Escrevendo e interpretando uma equação para uma função linear
Agora que escrevemos equações para funções lineares na forma de interceptação de inclinação e na forma de inclinação de ponto, podemos escolher qual método usar com base nas informações que recebemos. Essas informações podem ser fornecidas na forma de um gráfico, um ponto e uma inclinação, dois pontos e assim por diante. Veja o gráfico da função\(f\) na Figura\(\PageIndex{9}\).
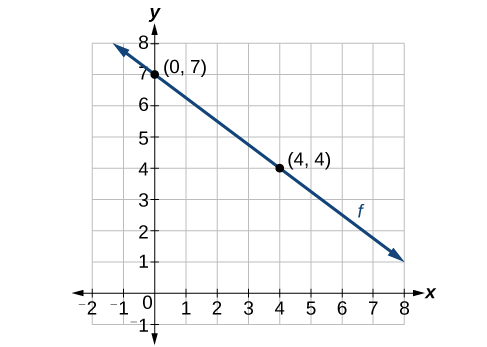
Não recebemos a inclinação da linha, mas podemos escolher quaisquer dois pontos na linha para encontrar a inclinação. Vamos escolher\((0,7)\)\((4, 4)\) e. Podemos usar esses pontos para calcular a inclinação.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-7}{4-0} \\&=-\dfrac{3}{4}\end{align*}\]
Agora podemos substituir a inclinação e as coordenadas de um dos pontos na forma ponto-inclinação.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-4&=-\dfrac{3}{4}(x-4) \end{align*}\]
Se quisermos reescrever a equação na forma de interceptação de inclinação, encontraríamos
\[\begin{align*} y-4&=-\dfrac{3}{4}(x-4) \\ y-4 &=-\dfrac{3}{4}x+3 \\ y&=-\dfrac{3}{4}x+7\end{align*}\]
Se quiséssemos encontrar a forma de interceptação de inclinação sem primeiro escrever a forma de inclinação de ponto, poderíamos ter reconhecido que a linha cruza o eixo y quando o valor de saída é 7. Portanto,\(b=7\). Agora temos o valor inicial\(b\) e a inclinação\(m\) para que possamos substituir\(m\) e\(b\) na forma de interceptação de inclinação de uma linha.
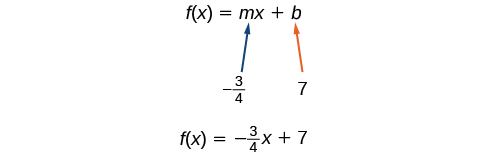
Portanto, a função é\(f(x)=−\frac{3}{4}x+7\), e a equação linear seria\(y=−\frac{3}{4}x+7\).
Dado o gráfico de uma função linear, escreva uma equação para representar a função.
- Identifique dois pontos na linha.
- Use os dois pontos para calcular a inclinação.
- Determine onde a linha cruza o eixo y para identificar o intercepto y por meio de inspeção visual.
- Substitua a inclinação e o intercepto y na forma de interceptação de inclinação de uma equação de linha.
Escreva uma equação para uma função linear dado um gráfico\(f\) mostrado na Figura\(\PageIndex{11}\).
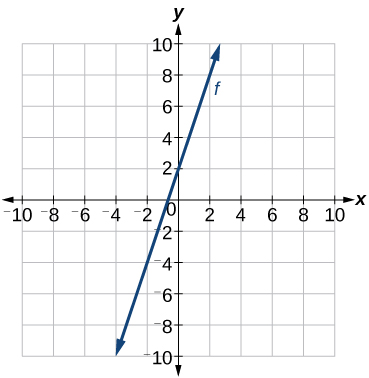
Solução
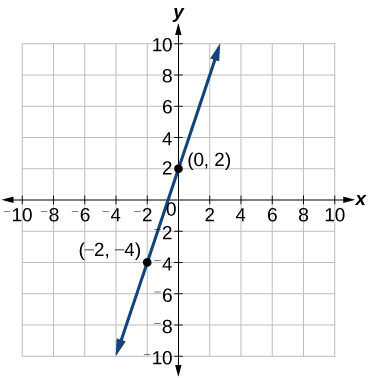
Identifique dois pontos na linha, como\((0, 2)\)\((−2,−4)\) e. Use os pontos para calcular a inclinação.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{4-2}{-2-0} \\ &=\dfrac{-6}{-2} \\ &=3 \end{align*}\]
Substitua a inclinação e as coordenadas de um dos pontos na forma ponto-inclinação.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-4)&=3(x-(-2)) \\ y+4 &= 3(x+2)\end{align*}\]
Podemos usar álgebra para reescrever a equação na forma de interceptação de inclinação.
\[\begin{align*} y+4&= 3(x+2) \\ y+4&= 3x+6 \\ y & = 3x + 2 \end{align*}\]
Análise
Isso faz sentido porque podemos ver na Figura\(\PageIndex{12}\) que a linha cruza o eixo y no ponto\((0, 2)\), que é o intercepto y, então\(b=2\).
Suponha que Ben abra uma empresa na qual ele incorra em um custo fixo de $1.250 por mês para as despesas gerais, o que inclui o aluguel do escritório. Seus custos de produção são de $37,50 por item. Escreva uma função linear\(C\) onde\(C(x)\) esteja o custo dos\(x\) itens produzidos em um determinado mês.
Solução
O custo fixo está presente todos os meses, $1.250. Os custos que podem variar incluem o custo de produção de cada item, que é de $37,50 para Ben. O custo variável, chamado de custo marginal, é representado por 37,5. O custo que Ben incorre é a soma desses dois custos, representados por\(C(x)=1250+37.5x\).
Análise
Se Ben produzir 100 itens em um mês, seu custo mensal será representado por
\[\begin{align*} C(100)&=1250+37.5(100) \\ &=5000 \end{align*}\]
Portanto, seu custo mensal seria de $5.000.
Se\(f\) for uma função linear, com\(f(3)=−2\), e\(f(8)=1\), encontre uma equação para a função na forma de interceptação de inclinação.
Solução
Podemos escrever os pontos dados usando coordenadas.
\[\begin{align*} f(3)&= -2{\rightarrow}(3,2) \\ f(8)&=1{\rightarrow}(8,1) \end{align*}\]
Podemos então usar os pontos para calcular a inclinação.
\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{1-(-2)}{8-3} \\ &=\dfrac{3}{5} \end{align*}\]
Substitua a inclinação e as coordenadas de um dos pontos na forma ponto-inclinação.
\[\begin{align*} y-y_1&=m(x-x_1) \\ y-(-2)&=\dfrac{3}{5}(x-3) \end{align*}\]
Podemos usar álgebra para reescrever a equação na forma de interceptação de inclinação.
\[\begin{align*} y+2&=\dfrac{3}{5}(x-3) \\ y+2&=\dfrac{3}{5}x-\dfrac{9}{5} \\ y&=\dfrac{3}{5}x-\dfrac{19}{5} \end{align*}\]
Se\(f(x)\) for uma função linear, com\(f(2)=–11\), e\(f(4)=−25\), encontre uma equação para a função na forma de interceptação de inclinação.
- Resposta
-
\(y=−7x+3\)
Modelando problemas do mundo real com funções lineares
No mundo real, os problemas nem sempre são explicitamente declarados em termos de uma função ou representados com um gráfico. Felizmente, podemos analisar o problema primeiro representando-o como uma função linear e depois interpretando os componentes da função. Desde que saibamos ou consigamos descobrir o valor inicial e a taxa de variação de uma função linear, podemos resolver muitos tipos diferentes de problemas do mundo real.
Dada uma função linear\(f\) e o valor inicial e a taxa de mudança, avalie\(f(c)\).
- Determine o valor inicial e a taxa de mudança (inclinação).
- Substitua os valores em\(f(x)=mx+b\).
- Avalie a função em\(x=c\).
Atualmente, Marcus tem 200 músicas em sua coleção musical. Todo mês, ele adiciona 15 músicas novas. Escreva uma fórmula para o número de músicas\(N\),, em sua coleção em função do tempo\(t\), o número de meses. Quantas músicas ele terá em um ano?
Solução
O valor inicial para essa função é 200 porque ele atualmente possui 200 músicas, então\(N(0)=200\), o que significa isso\(b=200\).
O número de músicas aumenta em 15 músicas por mês, então a taxa de variação é de 15 músicas por mês. Portanto, sabemos disso\(m=15\). Podemos substituir o valor inicial e a taxa de variação na forma de interceptação de inclinação de uma linha.
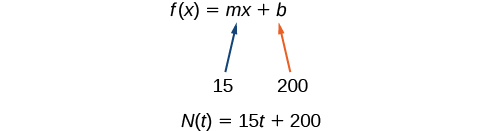
Podemos escrever a fórmula\(N(t)=15t+200\).
Com essa fórmula, podemos então prever quantas músicas Marcus terá em 1 ano (12 meses). Em outras palavras, podemos calcular a função em\(t=12\).
\[\begin{align*} N(12)&=15(12)+200 \\ &=180+200 \\ &= 380 \end{align*}\]
Marcus terá 380 músicas em 12 meses.
Análise
Observe que\(N\) é uma função linear crescente. À medida que a entrada (o número de meses) aumenta, a saída (número de músicas) também aumenta.
Trabalhando como vendedor de seguros, Ilya ganha um salário base mais uma comissão sobre cada nova apólice. Portanto, a renda semanal de Ilya, eu, depende do número de novas apólices que ele vende durante a semana.\(n\) Na semana passada, ele vendeu 3 novas apólices e ganhou $760 pela semana. Na semana anterior, ele vendeu 5 novas apólices e ganhou $920. Encontre uma equação para\(I(n)\) e interprete o significado dos componentes da equação.
Solução
As informações fornecidas nos fornecem dois pares de entrada-saída:\((3,760)\)\((5,920)\) e. Começamos encontrando a taxa de mudança.
\[\begin{align*} m&=\dfrac{920-760}{5-3} \\ &=\dfrac{$160}{2 \text{ policies}} \\ &=$80 \text{ per policy} \end{align*}\]
Acompanhar as unidades pode nos ajudar a interpretar essa quantidade. A renda aumentou em $160 quando o número de apólices aumentou em 2, então a taxa de mudança é de $80 por apólice. Portanto, Ilya ganha uma comissão de $80 por cada apólice vendida durante a semana.
Em seguida, podemos resolver o valor inicial.
\[\begin{align*} I(n)&=80n+b \\ 760&=80(3)+b \text{ when } n=3, I(3)=760 \\ 760-80(3)&=b \\ 520 & =b \end{align*}\]
O valor de\(b\) é o valor inicial da função e representa a renda de Ilya quando\(n=0\) ou quando nenhuma nova apólice é vendida. Podemos interpretar isso como o salário base da semana de Ilya, que não depende do número de apólices vendidas.
Agora podemos escrever a equação final.
\[I(n)=80n+520 \nonumber\]
Nossa interpretação final é que o salário base de Ilya é de $520 por semana e ele ganha uma comissão adicional de $80 por cada apólice vendida.
equação para uma função linear
A tabela\(\PageIndex{1}\) relaciona o número de ratos em uma população com o tempo, em semanas. Use a tabela para escrever uma equação linear.
| w, número de semanas | 0 | 2 | 4 | 6 |
|---|---|---|---|---|
| P (w), número de ratos | 1000 | 1080 | 1160 | 1240 |
Solução
Podemos ver na tabela que o valor inicial para o número de ratos é 1000, então\(b=1000\).
Em vez de resolver\(m\), podemos dizer, olhando para a tabela, que a população aumenta em 80% a cada 2 semanas que passam. Isso significa que a taxa de variação é de 80 ratos por 2 semanas, o que pode ser simplificado para 40 ratos por semana.
\[P(w)=40w+1000 \nonumber\]
Se não notássemos a taxa de variação da tabela, ainda poderíamos resolver a inclinação usando quaisquer dois pontos da tabela. Por exemplo, usando\((2,1080)\) e\((6,1240)\)
\[\begin{align*} m&=\dfrac{1240-1080}{6-2} \\ &=\dfrac{160}{4} \\ &= 40\end{align*}\]
O valor inicial é sempre fornecido em uma tabela de valores como Tabela\(\PageIndex{1}\)?
Não. Às vezes, o valor inicial é fornecido em uma tabela de valores, mas às vezes não é. Se você ver uma entrada de 0, o valor inicial seria a saída correspondente. Se o valor inicial não for fornecido porque não há valor de entrada na tabela igual a 0, encontre a inclinação, substitua um par de coordenadas e a inclinação em\(f(x)=mx+b\) e resolva para\(b\).
\(\PageIndex{5}\): Um novo alimento vegetal foi introduzido em uma árvore jovem para testar seu efeito na altura da árvore. A tabela\(\PageIndex{2}\) mostra a altura da árvore, em pés,\(x\) meses desde o início das medições. Escreva uma função linear,\(H(x)\), onde\(x\) está o número de meses desde o início do experimento.
| \(x\) | 0 | 2 | 4 | 8 | 12 |
|---|---|---|---|---|---|
| \(H(x)\) | 12,5 | 13,5 | 14,5 | 16,5 | 18,5 |
Solução
\(H(x)=0.5x+12.5\)
Equações-chave
- forma de interceptação de inclinação de uma linha:\(f(x)=mx+b\)
- inclinação:\(m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\)
- forma ponto-inclinada de uma linha:\(y−y_1 =m(x-x_1)\)
Conceitos-chave
- Os pares ordenados dados por uma função linear representam pontos em uma linha.
- As funções lineares podem ser representadas em palavras, notação de função, forma tabular e forma gráfica.
- A taxa de variação de uma função linear também é conhecida como inclinação.
- Uma equação na forma de interceptação de inclinação de uma linha inclui a inclinação e o valor inicial da função.
- O valor inicial, ou intercepto y, é o valor de saída quando a entrada de uma função linear é zero. É o valor y do ponto em que a linha cruza o eixo y.
- Uma função linear crescente resulta em um gráfico que se inclina para cima da esquerda para a direita e tem uma inclinação positiva.
- Uma função linear decrescente resulta em um gráfico que se inclina para baixo da esquerda para a direita e tem uma inclinação negativa.
- Uma função linear constante resulta em um gráfico que é uma linha horizontal.
- Analisar a inclinação dentro do contexto de um problema indica se uma função linear está aumentando, diminuindo ou constante.
- A inclinação de uma função linear pode ser calculada dividindo a diferença entre os valores y pela diferença nos valores x correspondentes de quaisquer dois pontos na linha.
- A inclinação e o valor inicial podem ser determinados com um gráfico ou quaisquer dois pontos na linha.
- Um tipo de notação de função é a forma de interceptação de inclinação de uma equação.
- A forma ponto-inclinação é útil para encontrar uma equação linear quando dada a inclinação de uma reta e um ponto.
- A forma de inclinação do ponto também é conveniente para encontrar uma equação linear quando dados dois pontos pelos quais uma linha passa.
- A equação para uma função linear pode ser escrita se a inclinação\(m\) e o valor inicial\(b\) forem conhecidos.
- Uma função linear pode ser usada para resolver problemas do mundo real.
- Uma função linear pode ser escrita a partir da forma tabular.
Notas de pé
1 www.chinahighlights.com/shang... glev-train.htm
2 www.cbsnews.com/8301-501465_1... ay-study-says/
Glossário
função linear decrescente
uma função com uma inclinação negativa: Se\(f(x)=mx+b\), então\(m<0\).
função linear crescente
uma função com uma inclinação positiva: Se\(f(x)=mx+b\), então\(m>0\).
função linear
uma função com uma taxa de variação constante que é um polinômio de grau 1 e cujo gráfico é uma linha reta
forma de ponto de inclinação
a equação para uma linha que representa uma função linear na forma\ (y−y_1=m (x−x_1)
inclinação
a razão entre a mudança nos valores de saída e a mudança nos valores de entrada; uma medida da inclinação de uma linha
forma de interceptação de inclinação
a equação para uma linha que representa uma função linear na forma\(f(x)=mx+b\)
intercepção y
o valor de uma função quando o valor de entrada é zero; também conhecido como valor inicial