2.3: Equações lineares em uma variável
- Page ID
- 189295
- Resolva equações em uma variável algebricamente.
- Resolva uma equação racional.
- Encontre uma equação linear.
- Dadas as equações de duas retas, determine se seus gráficos são paralelos ou perpendiculares.
- Escreva a equação de uma reta paralela ou perpendicular a uma determinada linha.
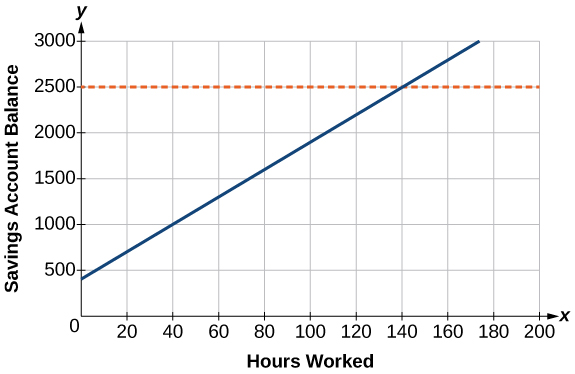
Caroline é uma estudante universitária em tempo integral que planeja férias de primavera. Para ganhar dinheiro suficiente para a viagem, ela conseguiu um emprego de meio período no banco local que paga\($15.00/hr\) e abriu uma conta poupança com um depósito inicial de 15 de\($400\) janeiro. Ela providenciou o depósito direto de seus cheques da folha de pagamento. Se as férias de primavera começarem em 20 de março e a viagem custar aproximadamente\($2,500\), quantas horas ela terá que trabalhar para ganhar o suficiente para pagar suas férias? Se ela só puder trabalhar\(4\) horas por dia, quantos dias por semana ela terá que trabalhar? Quantas semanas isso vai demorar? Nesta seção, investigaremos problemas como esse e outros, que geram gráficos como a linha na Figura\(\PageIndex{1}\).
Resolvendo equações lineares em uma variável
Uma equação linear é uma equação de uma linha reta, escrita em uma variável. O único poder da variável é\(1\). Equações lineares em uma variável podem assumir a forma\(ax +b=0\) e são resolvidas usando operações algébricas básicas. Começamos classificando as equações lineares em uma variável como um dos três tipos: identidade, condicional ou inconsistente.
- Uma equação de identidade é verdadeira para todos os valores da variável. Aqui está um exemplo de uma equação de identidade:\[3x=2x+x \nonumber \] O conjunto de soluções consiste em todos os valores que tornam a equação verdadeira. Para essa equação, o conjunto de soluções são todos números reais porque qualquer número real substituído\(x\) tornará a equação verdadeira.
- Uma equação condicional é verdadeira somente para alguns valores da variável. Por exemplo, se quisermos resolver a equação\(5x+2=3x−6\), temos o seguinte:\[\begin{align*} 5x+2&=3x-6 \\ 2x &=-8 \\ x&=-4 \end{align*} \] O conjunto de soluções consiste em um número:\({−4}\). É a única solução e, portanto, resolvemos uma equação condicional.
- Uma equação inconsistente resulta em uma declaração falsa. Por exemplo, se quisermos resolver\(5x−15=5(x−4)\), temos o seguinte:\[\begin{align*} 5x−15 &=5x−20 \\ 5x−15-5x &= 5x−20-5x \\ −15 &\neq −20 \end{align*}\] De fato,\(−15≠−20\). Não há solução porque essa é uma equação inconsistente.
Resolver equações lineares em uma variável envolve as propriedades fundamentais da igualdade e operações algébricas básicas. Segue uma breve revisão dessas operações.
Uma equação linear em uma variável pode ser escrita na forma
\[ax+b=0\]
onde a e b são números reais,\(a≠0\).
As etapas a seguir são usadas para manipular uma equação e isolar a variável desconhecida, de forma que a última linha seja\(x=\) _________, se\(x\) for a desconhecida. Não há uma ordem definida, pois as etapas usadas dependem do que é dado:
- Podemos somar, subtrair, multiplicar ou dividir uma equação por um número ou expressão, desde que façamos a mesma coisa nos dois lados do sinal de igual. Note que não podemos dividir por zero.
- Aplique a propriedade distributiva conforme necessário:\(a(b+c)=ab+ac\).
- Isole a variável em um lado da equação.
- Quando a variável é multiplicada por um coeficiente no estágio final, multiplique os dois lados da equação pelo inverso do coeficiente.
Resolva a seguinte equação:\(2x+7=19\).
Solução
Essa equação pode ser escrita na forma\(ax +b=0\) subtraindo 19 de ambos os lados. No entanto, podemos resolver a equação em sua forma original realizando operações algébricas.
\[\begin{align*} 2x+7&=19\\ 2x&=12\qquad \text{Subtract 7 from both sides}\\ x&=6\qquad \text{Multiply both sides by } \dfrac{1}{2} \text{ or divide by } 2 \end{align*}\]
A solução é\(6\).
Resolva a equação linear em uma variável:\(2x+1=−9\).
- Responda
-
\(x=−5\)
Resolva a seguinte equação:\(4(x−3)+12=15−5(x+6)\).
Solução
Aplique propriedades algébricas padrão.
\[\begin{align*} 4(x-3)+12&=15-5(x+6)\\ 4x-12+12&=15-5x-30\qquad \text{Apply the distributive property}\\ 4x&=-15-5x\qquad \text{Combine like terms}\\ 9x&=-15\qquad \text{Place x terms on one side and simplify}\\ x&=-\dfrac{15}{9}\qquad \text{Multiply both sides by } \dfrac{1}{9} \text { , the reciprocal of } 9\\ x&=-\dfrac{5}{3} \end{align*}\]
Análise
Esse problema exige que a propriedade distributiva seja aplicada duas vezes e, em seguida, as propriedades da álgebra sejam usadas para chegar à linha final,\(x=-\dfrac{5}{3}\).
Resolva a equação em uma variável:\(−2(3x−1)+x=14−x\).
- Responda
-
\(x=-3\)
Resolvendo uma equação racional
Nesta seção, examinamos equações racionais que, após alguma manipulação, resultam em uma equação linear. Se uma equação contém pelo menos uma expressão racional, ela é considerada uma equação racional. Lembre-se de que um número racional é a proporção de dois números, como\(\dfrac{2}{3}\) ou\(\dfrac{7}{2}\). Uma expressão racional é a razão, ou quociente, de dois polinômios. Aqui estão três exemplos.
\[\dfrac{x+1}{x^2-4} \nonumber \]
\[\dfrac{1}{x-3} \nonumber \]
ou
\[\dfrac{4}{x^2+x-2} \nonumber \]
As equações racionais têm uma variável no denominador em pelo menos um dos termos. Nosso objetivo é realizar operações algébricas para que as variáveis apareçam no numerador. Na verdade, eliminaremos todos os denominadores multiplicando os dois lados da equação pelo denominador menos comum (LCD). Encontrar o LCD é identificar uma expressão que contém a maior potência de todos os fatores em todos os denominadores. Fazemos isso porque quando a equação é multiplicada pelo LCD, os fatores comuns no LCD e em cada denominador serão iguais a um e serão cancelados.
Resolva a equação racional:
\[\dfrac{7}{2x}-\dfrac{5}{3x}=\dfrac{22}{3} \nonumber \]
Solução
Temos três denominadores;\(2x\)\(3x\),,\(3\) e. O LCD deve conter\(2x\)\(3x\),\(3\) e. Um LCD de\(6x\) contém todos os três denominadores. Em outras palavras, cada denominador pode ser dividido uniformemente no LCD. Em seguida, multiplique os dois lados da equação pelo LCD\(6x\).
\ [\ begin {align*}
(6x)\ left [\ dfrac {7} {2x} -\ dfrac {5} {3x}\ direita] &=\ left [\ dfrac {22} {3}\ direita] (6x)\ (6x)\ (6x)\ esquerda (\ dfrac {7} {2x}\ direita) -
(6x)\ esquerda (\ dfrac {7} {2x}\ direita) - (6x)\ esquerda (\ dfrac {7} {2x}\ direita) - (6x)\ esquerda (\ dfrac {dfrac {5} {3x}\ right) &=\ left (\ dfrac {22} {3}\ right) (6x)\ quad\ text {Use a propriedade distributiva. Cancele os fatores comuns}\\
3 (7) -2 (5) &=22 (2x)\ qquad\ text {Multiplique os fatores restantes por cada numerador.} \\
21-10&=44x\\
11&=44x\\
\ dfrac {11} {44} &=x\\
\ dfrac {1} {4} &=x
\ end {align*}\]
Um erro comum cometido ao resolver equações racionais envolve encontrar o LCD quando um dos denominadores é um binômio - dois termos adicionados ou subtraídos - como\((x+1)\). Sempre considere um binômio como um fator individual — os termos não podem ser separados. Por exemplo, suponha que um problema tenha três termos e os denominadores sejam\(x\)\(x−1\),\(3x−3\) e. Primeiro, fatore todos os denominadores. Em seguida\(x\), temos\((x−1)\), e\(3(x−1)\) como denominadores. (Observe os parênteses colocados ao redor do segundo denominador.) Somente os dois últimos denominadores têm um fator comum de\((x−1)\). O x no primeiro denominador é separado do\(x\) nos\((x−1)\) denominadores. Uma maneira eficaz de lembrar isso é escrever denominadores fatoriais e binomiais entre parênteses e considerar cada parêntese como uma unidade separada ou um fator separado. O LCD, neste caso, é encontrado multiplicando o fator de\(x\)\((x−1)\), um e o 3. Portanto, o LCD é o seguinte:
\(x(x−1)3=3x(x−1)\)
Então, os dois lados da equação seriam multiplicados por\(3x(x−1)\). Deixe o LCD na forma fatorada, pois isso facilita a visualização de como cada denominador do problema é cancelado.
Outro exemplo é um problema com dois denominadores, como\(x\)\(x^2+2x\) e. Uma vez que o segundo denominador é fatorado como\(x^2+2x=x(x+2)\), há um fator comum de\(x\) em ambos os denominadores e o LCD é\(x(x+2)\).
Às vezes, temos uma equação racional na forma de uma proporção; isto é, quando uma fração é igual a outra fração e não há outros termos na equação.
\[\dfrac{a}{b}=\dfrac{c}{d}\]
Podemos usar outro método para resolver a equação sem encontrar o LCD: multiplicação cruzada. Multiplicamos termos cruzando o sinal de igual.
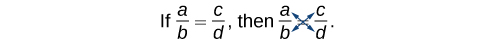
Multiplique a (d) e b (c), o que resulta em\(ad=bc\).
Qualquer solução que faça com que um denominador na expressão original seja igual a zero deve ser excluída das possibilidades.
Uma equação racional contém pelo menos uma expressão racional em que a variável aparece em pelo menos um dos denominadores.
- Fatore todos os denominadores na equação.
- Encontre e exclua valores que definem cada denominador igual a zero.
- Encontre o LCD.
- Multiplique toda a equação pelo LCD. Se o LCD estiver correto, não haverá mais denominadores.
- Resolva a equação restante.
- Certifique-se de verificar as soluções nas equações originais para evitar que uma solução produza zero em um denominador
Resolva a seguinte equação racional:
\(\dfrac{2}{x}-\dfrac{3}{2}=\dfrac{7}{2x}\)
SoluçãoTemos três denominadores:\(x\)\(2\),\(2x\) e. Nenhuma fatoração é necessária. O produto dos dois primeiros denominadores é igual ao terceiro denominador, então, o LCD é\(2x\). Somente um valor é excluído de um conjunto de soluções,\(0\). Em seguida, multiplique toda a equação (ambos os lados do sinal de igual) por\(2x\).
\[\begin{align*} 2x\left[\dfrac{2}{x}-\dfrac{3}{2}\right]&=\left[\dfrac{7}{2x}\right](2x)\\ 2x\left(\dfrac{2}{x}\right)-2x\left(\dfrac{3}{2}\right)&=\left(\dfrac{7}{2x}\right)(2x)\qquad \text{Distribute } 2x\\ 2(2)-3x&=7\qquad \text{Denominators cancel out.}\\ 4-3x&=7\\ -3x&=3\\ x&=-1 \text { or } \{-1\} \end{align*}\]
A solução proposta é\(−1\), que não é um valor excluído, portanto, o conjunto de soluções contém um número ou está\(\{−1\}\) escrito em notação de conjunto.\(x=−1\)
Resolva a equação racional:
\(\dfrac{2}{3x}=\dfrac{1}{4}-\dfrac{1}{6x}\)
- Responda
-
\(x=\dfrac{10}{3}\)
Resolva a seguinte equação racional:
\(\dfrac{1}{x}=\dfrac{1}{10}-\dfrac{3}{4x}\)
Solução
Primeiro encontre o denominador comum. Os três denominadores na forma fatorada são\(x,10=2⋅5\),\(4x=2⋅2⋅x\) e. A menor expressão que é divisível por cada um dos denominadores é\(20x\). Somente\(x=0\) é um valor excluído. Multiplique toda a equação por\(20x\).
\[\begin{align*} 20x\left(\dfrac{1}{x}\right)&= \left(\dfrac{1}{10}-\dfrac{3}{4x}\right)20x\\ 20&= 2x-15\\ 35&= 2x\\ \dfrac{35}{2}&= x \end{align*}\]
A solução é\(\dfrac{35}{2}\).
Resolva a equação racional:
\[-\dfrac{5}{2x}+\dfrac{3}{4x}=-\dfrac{7}{4} \nonumber \]
- Responda
-
\(x=1\)
Resolva as seguintes equações racionais e indique os valores excluídos:
- \(\dfrac{3}{x-6}=\dfrac{5}{x}\)
- \(\dfrac{x}{x-3}=\dfrac{5}{x-3}-\dfrac{1}{2}\)
- \(\dfrac{x}{x-2}=\dfrac{5}{x-2}-\dfrac{1}{2}\)
Solução
uma.
Os denominadores\(x\) e não\(x−6\) têm nada em comum. Portanto, o LCD é o produto\(x(x−6)\). No entanto, para esse problema, podemos multiplicar cruzadamente.
\[\begin{align*} \dfrac{3}{x-6}&=\dfrac{5}{x}\\ 3x&=5(x-6)\qquad \text{Distribute.}\\ 3x&=5x-30\\ -2x&=-30\\ x&=15 \end{align*}\]
A solução é\(15\). Os valores excluídos são\(6\)\(0\) e.
b.
O LCD é\(2(x−3)\). Multiplique os dois lados da equação por\(2(x−3)\).
\[\begin{align*} 2(x-3)\left [\dfrac{x}{x-3} \right ]&= \left [\dfrac{5}{x-3}-\dfrac{1}{2} \right ]2(x-3)\\ \dfrac{2(x-3)x}{x-3}&= \dfrac{2(x-3)5}{x-3}-\dfrac{2(x-3)}{2}\\ 2x&= 10-(x-3)\\ 2x&= 13-x\\ 3x&= 13\\ x&= \dfrac{13}{3} \end{align*}\]
A solução é\(\dfrac{13}{3}\). O valor excluído é\(3\).
c.
O denominador menos comum é\(2(x−2)\). Multiplique os dois lados da equação por\(x(x−2)\).
\[\begin{align*} 2(x-2)\left [\dfrac{x}{x-2} \right ]&= \left [\dfrac{5}{x-2}-\dfrac{1}{2} \right ]2(x-2)\\ 2x&= 10-(x-2)\\ 2x&= 12-x\\ 3x&= 12\\ x&= 4 \end{align*}\]
A solução é\(4\). O valor excluído é\(2\).
Resolver\(\dfrac{-3}{2x+1}=\dfrac{4}{3x+1}\). Indique os valores excluídos.
- Responda
-
\(x=-\dfrac{7}{17}\). Os valores excluídos são\(x=−12\)\(x=−13\) e.
Resolva a equação racional depois de fatorar os denominadores:\(\dfrac{2}{x+1}-\dfrac{1}{x-1}=\dfrac{2x}{x^2-1}\). Indique os valores excluídos.
Solução
Devemos fatorar o denominador\(x^2−1\). Nós reconhecemos isso como a diferença dos quadrados e o fatoramos como\((x−1)(x+1)\). Assim, o LCD que contém cada denominador é\((x−1)(x+1)\). Multiplique toda a equação pelo LCD, cancele os denominadores e resolva a equação restante.
\[\begin{align*} (x+1)(x-1)\left [\dfrac{2}{x+1}-\dfrac{1}{x-1} \right ]&= \left [\dfrac{2x}{x^2-1} \right ](x+1)(x-1)\\ 2(x-1)-(x+1)&= 2x\\ 2x-2-x-1&= 2x \text{ Distribute the negative sign}\\ -3-x&= 0\\ x&= -3 \end{align*}\]
A solução é\(−3\). Os valores excluídos são\(1\)\(−1\) e.
Resolva a equação racional:
\(\dfrac{2}{x-2}+\dfrac{1}{x+1}=\dfrac{1}{x^2-x-2}\)
- Responda
-
\(x=\dfrac{1}{3}\)
Encontrando uma equação linear
Talvez a forma mais familiar de uma equação linear seja a forma de interceptação de inclinação, escrita como\[y=mx+b\] onde\(m=\text{slope}\) e\(b=\text{y−intercept.}\) Vamos começar com a inclinação.
A inclinação de uma linha se refere à razão da mudança vertical em\(y\) relação à mudança horizontal\(x\) entre quaisquer dois pontos em uma linha. Indica a direção na qual uma linha se inclina, bem como sua inclinação. A inclinação às vezes é descrita como aumento sobre corrida.
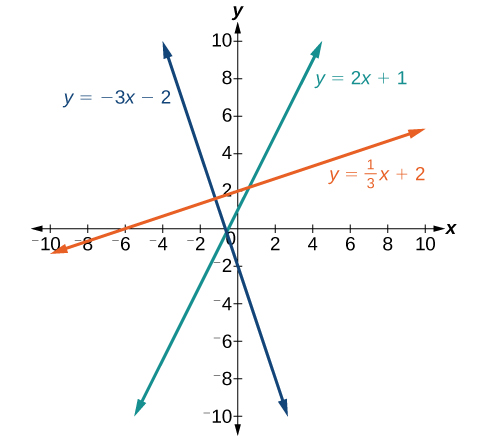
Se a inclinação for positiva, a linha se inclina para a direita. Se a inclinação for negativa, a linha se inclina para a esquerda. Conforme a inclinação aumenta, a linha se torna mais íngreme. Alguns exemplos são mostrados na Figura\(\PageIndex{2}\). As linhas indicam as seguintes inclinações:\(m=−3\)\(m=2\),\(m=\dfrac{1}{3}\) e.
A inclinação de uma linha,\(m\), representa a mudança em\(y\) relação à mudança em\(x\). Dados dois pontos,\((x_1,y_1)\) e\((x_2,y_2)\), a fórmula a seguir determina a inclinação de uma linha contendo esses pontos:
\[m=\dfrac{y_2-y_1}{x_2-x_1}\]
Encontre a inclinação de uma linha que passa pelos pontos\((2,−1)\)\((−5,3)\) e.
Solução
Substituímos os\(y\) valores -e os\(x\) valores -na fórmula.
\[\begin{align*} m&= \dfrac{3-(-1)}{-5-2}\\ &= \dfrac{4}{-7}\\ &= -\dfrac{4}{7} \end{align*}\]
A inclinação é\(-\dfrac{4}{7}\)
Análise
Não importa qual ponto é chamado\((x_1,y_1)\) ou\((x_2,y_2)\). Desde que sejamos consistentes com a ordem dos\(y\) termos e a ordem dos\(x\) termos no numerador e no denominador, o cálculo produzirá o mesmo resultado.
Encontre a inclinação da linha que passa pelos pontos\((−2,6)\)\((1,4)\) e.
- Responda
-
\(m=-\dfrac{2}{3}\)
Identifique a inclinação e a\(y\) interceptação, dada a equação\(y=-\dfrac{3}{4}x-4\).
Solução
Como a linha está em\(y=mx+b\) forma, a linha dada tem uma inclinação de\(m=-\dfrac{3}{4}\). O\(y\) intercepto -é\(b=−4\).
Análise
O\(y\) intercepto -é o ponto no qual a linha cruza o\(y\) eixo -. No\(y\) eixo -,\(x=0\). Sempre podemos identificar o\(y\) intercepto -quando a linha está na forma de interceptação de inclinação, pois ela sempre será igual\(b\). Ou simplesmente substitua\(x=0\) e resolva\(y\).
A fórmula de inclinação de pontos
Dada a inclinação e um ponto em uma reta, podemos encontrar a equação da reta usando a fórmula de inclinação do ponto.
\[y−y_1=m(x−x_1)\]
Essa é uma fórmula importante, pois será usada em outras áreas da álgebra universitária e, muitas vezes, no cálculo para encontrar a equação de uma reta tangente. Precisamos apenas de um ponto e da inclinação da linha para usar a fórmula. Depois de substituir a inclinação e as coordenadas de um ponto na fórmula, nós a simplificamos e a escrevemos na forma de interceptação de inclinação.
Dado um ponto e a inclinação, a fórmula da inclinação do ponto levará à equação de uma reta:
\[y−y_1=m(x−x_1)\]
Escreva a equação da linha com inclinação\(m=−3\) e passando pelo ponto\((4,8)\). Escreva a equação final na forma de interceptação de inclinação.
Solução
Usando a fórmula de inclinação do ponto, substitua\(−3\) por m e o ponto\((4,8)\) por\((x_1,y_1)\).
\[\begin{align*} y-y_1&= m(x-x_1)\\ y-8&= -3(x-4)\\ y-8&= -3x+12\\ y&= -3x+20 \end{align*}\]
Análise
Observe que qualquer ponto na linha pode ser usado para encontrar a equação. Se feito corretamente, a mesma equação final será obtida.
Dado\(m=4\), encontre a equação da reta na forma de interceptação de inclinação passando pelo ponto\((2,5)\).
- Responda
-
\(y=4x−3\)
Encontre a equação da linha que passa pelos pontos\((3,4)\)\((0,−3)\) e. Escreva a equação final na forma de interceptação de inclinação.
Solução
Primeiro, calculamos a inclinação usando a fórmula da inclinação e dois pontos.
\[\begin{align*} m&= \dfrac{-3-4}{0-3}\\ m&= \dfrac{-7}{-3}\\ m&= \dfrac{7}{3}\\ \end{align*}\]
Em seguida, usamos a fórmula de inclinação do ponto com a inclinação de\(\dfrac{7}{3}\) e qualquer um dos pontos. Vamos escolher o ponto\((3,4)\) para\((x_1,y_1)\).
\[\begin{align*} y-4&= \dfrac{7}{3}(x-3)\\ y-4&= \dfrac{7}{3}x-7\\ y&= \dfrac{7}{3}x-3\\ \end{align*}\]
Na forma de interceptação de inclinação, a equação é escrita como\(y=\dfrac{7}{3}x-3\)
Análise
Para provar que qualquer um dos pontos pode ser usado, vamos usar o segundo ponto\((0,−3)\) e ver se obtemos a mesma equação.
\[\begin{align*} y-(-3)&= \dfrac{7}{3}(x-0)\\ y+3&= \dfrac{7}{3}x\\ y&= \dfrac{7}{3}x-3\\ \end{align*}\]
Vemos que a mesma linha será obtida usando qualquer um dos pontos. Isso faz sentido porque usamos os dois pontos para calcular a inclinação.
Forma padrão de uma linha
Outra forma de representar a equação de uma linha é na forma padrão. O formulário padrão é fornecido como
\[Ax+By=C\]
onde\(A\)\(B\), e\(C\) são números inteiros. Os\(y\) termos\(x\) - e -estão em um lado do sinal de igual e o termo constante está no outro lado.
Encontre a equação da reta com\(m=−6\) e passando pelo ponto\(\left(\dfrac{1}{4},−2\right)\). Escreva a equação na forma padrão.
Solução
Começamos a usar a fórmula de inclinação de pontos.
\[\begin{align*} y-(-2)&= -6\left(x-\dfrac{1}{4}\right)\\ y+2&= -6x+\dfrac{3}{2}\\ \end{align*}\]
A partir daqui, multiplicamos por\(2\), já que nenhuma fração é permitida na forma padrão e, em seguida, movemos as duas variáveis para o lado esquerdo do sinal de igual e movemos as constantes para a direita.
\[\begin{align*} 2(y+2)&= \left(-6x+\dfrac{3}{2}\right)2\\ 2y+4&= -12x+3\\ 12x+2y&= -1 \end{align*}\]
Essa equação agora está escrita na forma padrão.
Encontre a equação da reta na forma padrão com inclinação\(m=−\dfrac{1}{3}\) e passando pelo ponto\((1,13)\).
- Responda
-
\(x+3y=2\)
Linhas verticais e horizontais
As equações das linhas verticais e horizontais não exigem nenhuma das fórmulas anteriores, embora possamos usar as fórmulas para provar que as equações estão corretas. A equação de uma linha vertical é dada como
onde\(c\) está uma constante. A inclinação de uma linha vertical é indefinida e, independentemente do\(y\) valor -de qualquer ponto na linha, a\(x\) coordenada -do ponto será\(c\).
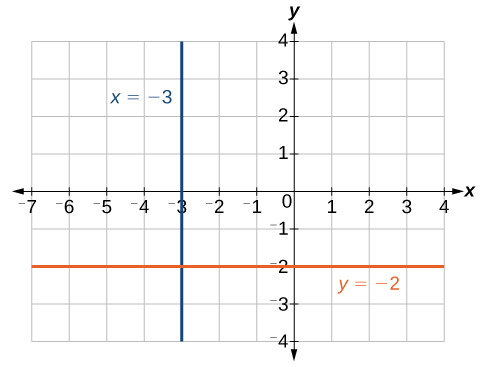
Suponha que desejemos encontrar a equação de uma linha contendo os seguintes pontos:\((−3,−5)\)\((−3,1)\)\((−3,3)\),,\((−3,5)\) e. Primeiro, encontraremos a inclinação.
Zero no denominador significa que a inclinação é indefinida e, portanto, não podemos usar a fórmula ponto-inclinação. No entanto, podemos traçar os pontos. Observe que todas as\(x\) coordenadas -são iguais e encontramos uma linha vertical através dela\(x=−3\). Veja a Figura\(\PageIndex{3}\).
A equação de uma linha horizontal é dada como
\[y=c\]
onde\(c\) está uma constante. A inclinação de uma linha horizontal é zero e, para qualquer\(x\) valor de um ponto na linha, a\(y\) coordenada -será\(c\).
Suponha que queiramos encontrar a equação de uma linha que contém o seguinte conjunto de pontos:\((−2,−2)\)\((0,−2)\)\((3,−2)\),,\((5,−2)\) e. Podemos usar a fórmula de inclinação de pontos. Primeiro, encontramos a inclinação usando quaisquer dois pontos na linha.
\[\begin{align*} m&= \dfrac{-2-(-2)}{0-(-2)}\\ &= \dfrac{0}{2}\\ &= 0 \end{align*}\]
Use qualquer ponto para\((x_1,y_1)\) na fórmula ou use o intercepto y.
\[\begin{align*} y-(-2)&= 0(x-3)\\ y+2&= 0\\ y&= -2 \end{align*}\]
O gráfico é uma linha horizontal transversal\(y=−2\). Observe que todas as coordenadas y são iguais. Veja a Figura\(\PageIndex{3}\).
Encontre a equação da linha que passa pelos pontos dados:\((1,−3)\)\((1,4)\) e.
Solução
A\(x\) coordenada -de ambos os pontos é\(1\). Portanto, temos uma linha vertical,\(x=1\).
Encontre a equação da linha que passa por\((−5,2)\)\((2,2)\) e.
- Responda
-
Linha horizontal:\(y=2\)
Determinando se os gráficos de retas são paralelos ou perpendiculares
As linhas paralelas têm a mesma inclinação e diferentes interceptos y. Linhas paralelas entre si nunca se cruzarão. Por exemplo, a Figura\(\PageIndex{4}\) mostra os gráficos de várias linhas com a mesma inclinação,\(m=2\).
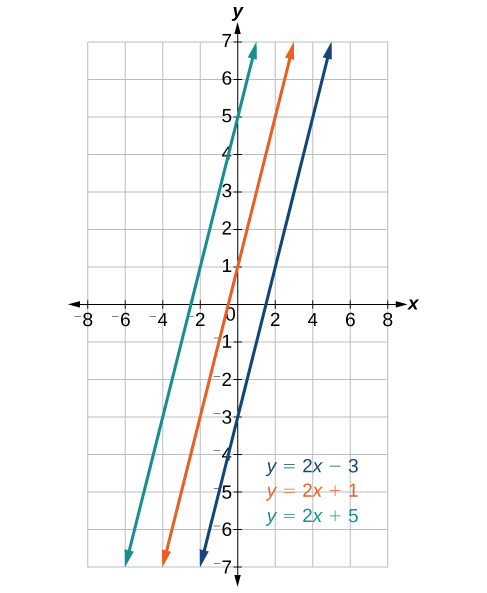
Todas as linhas mostradas no gráfico são paralelas porque têm a mesma inclinação e diferentes interceptos y.
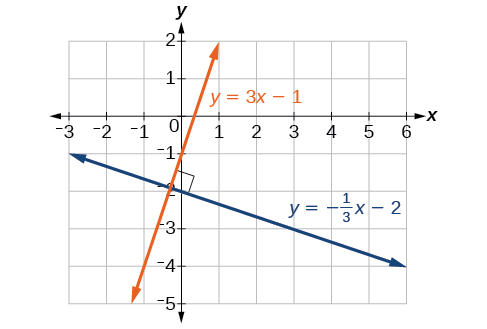
As linhas que são perpendiculares se cruzam para formar um\(90^{\circ}\) ângulo. A inclinação de uma linha é o recíproco negativo da outra. Podemos mostrar que duas retas são perpendiculares se o produto das duas inclinações for\(−1:m_1⋅m_2=−1\). Por exemplo, a Figura\(\PageIndex{5}\) mostra o gráfico de duas linhas perpendiculares. Uma linha tem uma inclinação de\(3\); a outra linha tem uma inclinação de\(-\dfrac{1}{3}\).
\[\begin{align*} m_1\cdot m_2&= -1\\ 3\cdot \left (-\dfrac{1}{3} \right )&= -1\\ \end{align*}\]
Faça um gráfico das equações das linhas dadas e indique se elas são paralelas, perpendiculares ou nenhuma delas:\(3y=−4x+3\)\(3x−4y=8\) e.
Solução
A primeira coisa que queremos fazer é reescrever as equações para que ambas estejam na forma de interceptação de inclinação.
Primeira equação:
\[\begin{align*} 3y&= -4x+3\\ y&= -\dfrac{4}{3}x+1\\ \end{align*}\]
Segunda equação:
\[\begin{align*} 3x-4y&= 8\\ -4y&= -3x+8\\ y&= \dfrac{3}{4}x-2 \end{align*}\]
Veja o gráfico das duas linhas na Figura\(\PageIndex{6}\).
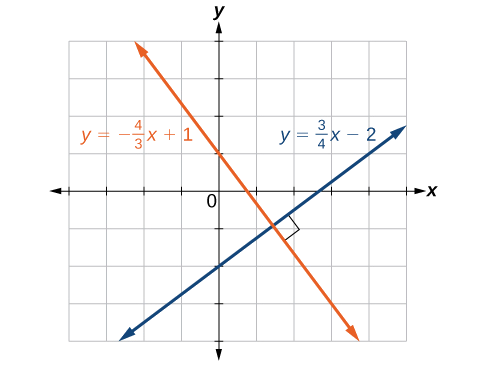
A partir do gráfico, podemos ver que as linhas parecem perpendiculares, mas devemos comparar as inclinações.
\[\begin{align*} m_1&=-\dfrac{4}{3}\\ m_2&=\dfrac{3}{4}\\ m_1\cdot m_2&=\left(-\dfrac{4}{3}\right)\left(\dfrac{3}{4}\right)\\ &=-1 \end{align*}\]
As inclinações são recíprocas negativas uma da outra, confirmando que as retas são perpendiculares.
Faça um gráfico das duas linhas e determine se elas são paralelas, perpendiculares ou nenhuma delas:\(2y−x=10\)\(2y=x+4\) e.
- Responda
-
Linhas paralelas: as equações são escritas na forma de interceptação de inclinação.
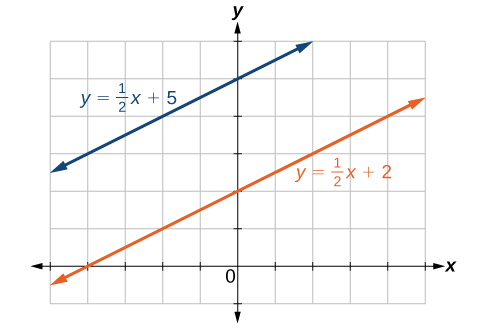
Figura\(\PageIndex{7}\)
Escrevendo as equações de retas paralelas ou perpendiculares a uma determinada linha
Como aprendemos, determinar se duas retas são paralelas ou perpendiculares é uma questão de encontrar as inclinações. Para escrever a equação de uma reta paralela ou perpendicular a outra reta, seguimos os mesmos princípios que fazemos para encontrar a equação de qualquer reta. Depois de encontrar a inclinação, use a fórmula de inclinação do ponto para escrever a equação da nova linha.
- Encontre a inclinação da linha dada. A maneira mais fácil de fazer isso é escrever a equação na forma de interceptação de inclinação.
- Use a inclinação e o ponto dado com a fórmula de inclinação do ponto.
- Simplifique a linha para a forma de interceptação de inclinação e compare a equação com a linha dada.
Escreva a equação da linha paralela a a\(5x+3y=1\) e passando pelo ponto\((3,5)\).
Solução
Primeiro, escreveremos a equação na forma de interceptação de inclinação para encontrar a inclinação.
\[\begin{align*} 5x+3y&= 1\\ 3y&= -5x+1\\ y&= -\dfrac{5}{3}x+\dfrac{1}{3} \end{align*}\]
A inclinação é\(m=−\dfrac{5}{3}\). O intercepto y é\(13\), mas isso realmente não entra em nosso problema, pois a única coisa que precisamos para que duas retas sejam paralelas é a mesma inclinação. A única exceção é que, se\(y\) as interceptações -forem iguais, as duas linhas serão a mesma linha. O próximo passo é usar essa inclinação e o ponto dado com a fórmula de inclinação do ponto.
\[\begin{align*} y-5&= -\dfrac{5}{3}(x-3)\\ y-5&= -\dfrac{5}{3}x+5\\ y&= -\dfrac{5}{3}x+10 \end{align*}\]
A equação da linha é\(y=−\dfrac{5}{3}x+10\). Veja a Figura\(\PageIndex{8}\).
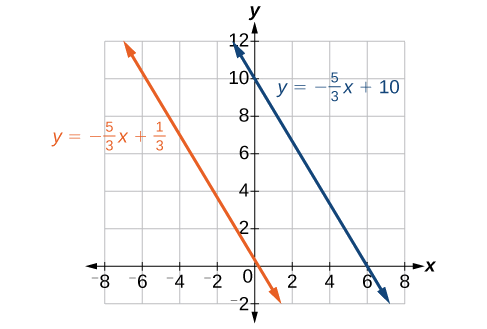
Encontre a equação da reta paralela ao ponto\(5x=7+y\) e que passa pelo mesmo\((−1,−2)\).
- Responda
-
\(y=5x+3\)
Encontre a equação da reta perpendicular\(5x−3y+4=0\space(−4,1)\) a.
Solução
O primeiro passo é escrever a equação na forma de interceptação de inclinação.
\[\begin{align*} 5x-3y+4&= 0\\ -3y&= -5x-4\\ y&= \dfrac{5}{3}x+\dfrac{4}{3} \end{align*}\]
Vemos que a inclinação é\(m=\dfrac{5}{3}\). Isso significa que a inclinação da reta perpendicular à linha dada é a recíproca negativa, ou\(-\dfrac{3}{5}\). Em seguida, usamos a fórmula de inclinação de pontos com essa nova inclinação e o ponto dado.
\[\begin{align*} y-1&= -\dfrac{3}{5}(x-(-4))\\ y-1&= -\dfrac{3}{5}x-\dfrac{12}{5}\\ y&= -\dfrac{3}{5}x-\dfrac{12}{5}+\dfrac{5}{5}\\ y&= -\dfrac{3}{5}x-\dfrac{7}{5} \end{align*}\]
Acesse esses recursos on-line para obter instruções e práticas adicionais com equações lineares.
- Resolvendo equações racionais
- Equação de uma reta dados dois pontos
- Encontrando a equação de uma reta perpendicular a outra reta através de um determinado ponto
- Encontrando a equação de uma reta paralela a outra linha através de um determinado ponto
Conceitos-chave
- Podemos resolver equações lineares em uma variável na forma\(ax +b=0\) usando propriedades algébricas padrão. Veja o exemplo e o exemplo.
- Uma expressão racional é um quociente de dois polinômios. Usamos o LCD para limpar as frações de uma equação. Veja o exemplo e o exemplo.
- Todas as soluções para uma equação racional devem ser verificadas dentro da equação original para evitar um termo indefinido ou zero no denominador. Veja o exemplo e o exemplo.
- Dados dois pontos, podemos encontrar a inclinação de uma linha usando a fórmula da inclinação. Veja o exemplo.
- Podemos identificar a inclinação e a\(y\) interceptação de uma equação na forma de interceptação de inclinação. Veja o exemplo.
- Podemos encontrar a equação de uma reta dada a inclinação e um ponto. Veja o exemplo.
- Também podemos encontrar a equação de uma reta dados dois pontos. Encontre a inclinação e use a fórmula ponto-inclinação. Veja o exemplo.
- A forma padrão de uma linha não tem frações. Veja o exemplo.
- As linhas horizontais têm uma inclinação de zero e são definidas como\(y=c\), onde\(c\) é uma constante.
- As linhas verticais têm uma inclinação indefinida (zero no denominador) e são definidas como \(x=c\), onde\(c\) é uma constante. Veja o exemplo.
- As linhas paralelas têm a mesma inclinação e diferentes\(y\) interceptações. Veja o exemplo.
- As linhas perpendiculares têm inclinações que são recíprocas negativas uma da outra, a menos que uma seja horizontal e a outra vertical. Veja o exemplo.


