2.4: Modelos e aplicações
- Page ID
- 189282
- Configure uma equação linear para resolver uma aplicação do mundo real.
- Use uma fórmula para resolver uma aplicação do mundo real.
Josh espera conseguir uma aula de álgebra\(A\) na faculdade. Ele tem pontuações de\(75\)\(82\),\(95\),,\(91\), e\(94\) em seus primeiros cinco testes. Somente o exame final permanece, e o máximo de pontos que podem ser ganhos é\(100\). É possível que Josh termine o curso com um\(A\)? Uma equação linear simples dará a Josh sua resposta.

Muitas aplicações do mundo real podem ser modeladas por equações lineares. Por exemplo, um pacote de telefone celular pode incluir uma taxa de serviço mensal mais uma cobrança por minuto de tempo de conversação; custa ao fabricante de widgets uma certa quantia produzir x widgets por mês mais taxas operacionais mensais; uma locadora de veículos cobra uma taxa diária mais uma quantia por milha percorrida. Esses são exemplos de aplicações que encontramos todos os dias que são modeladas por equações lineares. Nesta seção, vamos configurar e usar equações lineares para resolver esses problemas.
Configurando uma equação linear para resolver uma aplicação do mundo real
Para configurar ou modelar uma equação linear para se adequar a uma aplicação real, precisamos primeiro determinar as quantidades conhecidas e definir a quantidade desconhecida como uma variável. Em seguida, começamos a interpretar as palavras como expressões matemáticas usando símbolos matemáticos. Vamos usar o exemplo de aluguel de carros acima. Nesse caso, um custo conhecido, como\($0.10/mi\), é multiplicado por uma quantidade desconhecida, o número de milhas percorridas. Portanto, podemos escrever\(0.10x\). Essa expressão representa um custo variável porque muda de acordo com o número de milhas percorridas.
Se uma quantidade é independente de uma variável, geralmente apenas a somamos ou subtraímos, de acordo com o problema. Como esses valores não mudam, nós os chamamos de custos fixos. Considere uma agência de aluguel de carros que cobra\($0.10/mi\) mais uma taxa diária de\($50\). Podemos usar essas quantidades para modelar uma equação que pode ser usada para encontrar o custo diário do aluguel de carros\(C\).
\(C=0.10x+50 \tag{2.4.1}\)
Ao lidar com aplicativos do mundo real, existem certas expressões que podemos traduzir diretamente para a matemática. A tabela\(\PageIndex{1}\) lista algumas expressões verbais comuns e suas expressões matemáticas equivalentes.
| Verbal | Tradução para operações matemáticas |
|---|---|
| Um número excede o outro em um | \(x,x+a\) |
| Duas vezes um número | \(2x\) |
| Um número é\(a\) mais do que outro número | \(x,x+a\) |
| Um número é menos do dobro de outro número | \(x,2x−a\) |
| O produto de um número e\(a\), diminuído em\(b\) | \(ax−b\) |
| O quociente de um número e o número mais\(a\) é três vezes o número | \(\dfrac{x}{x+a}=3x\) |
| O produto de três vezes um número e o número diminuído em\(b\) é\(c\) | \(3x(x−b)=c\) |
- Identifique quantidades conhecidas.
- Atribua uma variável para representar a quantidade desconhecida.
- Se houver mais de uma quantidade desconhecida, encontre uma maneira de escrever a segunda incógnita em termos da primeira.
- Escreva uma equação interpretando as palavras como operações matemáticas.
- Resolva a equação. Certifique-se de que a solução possa ser explicada em palavras, incluindo as unidades de medida.
Encontre uma equação linear para resolver as seguintes quantidades desconhecidas: Um número excede outro número em\( 17\) e sua soma é\( 31\). Encontre os dois números.
Solução
Seja\( x\) igual ao primeiro número. Então, como o segundo número excede o primeiro em\(17\), podemos escrever o segundo número como\( x +17\). A soma dos dois números é\(31\). Normalmente interpretamos a palavra é como um sinal de igual.
\[\begin{align*} x+(x+17)&= 31\\ 2x+17&= 31\\ 2x&= 14\\ x&= 7 \end{align*}\]
\[\begin{align*} x+17&= 7 + 17\\ &= 24\\ \end{align*}\]
Os dois números são\(7\)\(24\) e.
Encontre uma equação linear para resolver as seguintes quantidades desconhecidas: Um número é três a mais do que o dobro de outro número. Se a soma dos dois números for\(36\), encontre os números.
- Responda
-
\(11\)e\(25\)
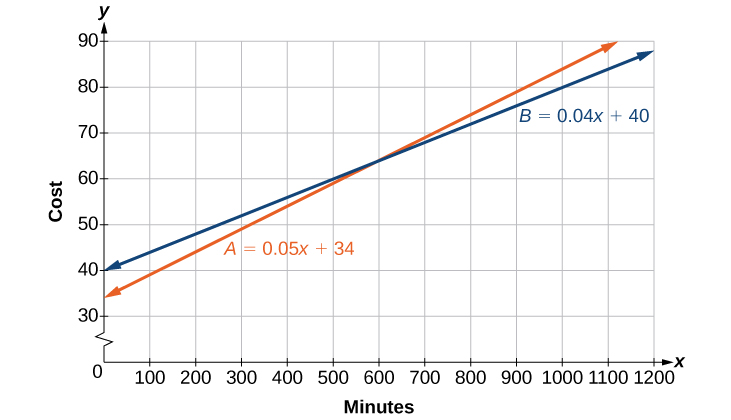
Existem duas empresas de telefonia celular que oferecem pacotes diferentes. A empresa A cobra uma taxa de serviço mensal de\($34\) mais o\($.05/min\) tempo de conversação. A empresa B cobra uma taxa de serviço mensal de\($40\) mais o\($.04/min\) tempo de conversação.
- Escreva uma equação linear que modela os pacotes oferecidos pelas duas empresas.
- Se o número médio de minutos usados por mês for\(1,160\), qual empresa oferece o melhor plano?
- Se o número médio de minutos usados por mês for\(420\), qual empresa oferece o melhor plano?
- Quantos minutos de conversação produziriam declarações mensais iguais de ambas as empresas?
Solução
uma.
O modelo da Empresa A pode ser escrito como\( A =0.05x+34\). Isso inclui o custo variável de\( 0.05x\) mais a taxa de serviço mensal de\($34\). O pacote da empresa B cobra uma taxa mensal mais alta de\($40\), mas um custo variável menor de\( 0.04x\). O modelo da empresa B pode ser escrito como\( B =0.04x+$40\).
b.
Se o número médio de minutos usados a cada mês for\(1,160\), temos o seguinte:
\[\begin{align*} \text{Company A}&= 0.05(1.160)+34\\ &= 58+34\\ &= 92 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(1,1600)+40\\ &= 46.4+40\\ &= 86.4 \end{align*}\]
Portanto, a Empresa B oferece o menor custo mensal de\($86.40\) em comparação com o custo\($92\) mensal oferecido pela Empresa A, quando o número médio de minutos usados a cada mês é\(1,160\).
c.
Se o número médio de minutos usados a cada mês for\(420\), temos o seguinte:
\[\begin{align*} \text{Company A}&= 0.05(420)+34\\ &= 21+34\\ &= 55 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(420)+40\\ &= 16.8+40\\ &= 56.8 \end{align*}\]
Se o número médio de minutos usados a cada mês for\(420\), a Empresa A oferece um custo mensal menor\($55\) em comparação com o custo mensal da Empresa B de\($56.80\).
d.
Para responder à pergunta de quantos minutos de conversação produziriam a mesma fatura de ambas as empresas, devemos pensar no problema em termos de\((x,y)\) coordenadas: em que ponto o\(x\) valor -e o\(y\) valor -são iguais? Podemos encontrar esse ponto definindo as equações iguais entre si e resolvendo para\(x\).
\[\begin{align*} 0.05x+34&= 0.04x+40\\ 0.01x&= 6\\ x&= 600 \end{align*}\]Verifique o\(x\) valor -em cada equação.
\(0.05(600)+34=64\)
\(0.04(600)+40=64\)
Portanto, uma média mensal de minutos\(600\) de tempo de conversação torna os planos iguais. Veja a Figura\(\PageIndex{2}\).
Encontre uma equação linear para modelar essa aplicação do mundo real: custa à empresa de eletrônicos ABC\($2.50\) por unidade produzir uma peça usada em uma marca popular de computadores desktop. A empresa tem despesas operacionais mensais\($350\) de serviços públicos e\($3,300\) salários. Quais são as despesas mensais da empresa?
- Responda
-
\(C=2.5x+3,650\)
Usando uma fórmula para resolver um aplicativo do mundo real
Muitos aplicativos são resolvidos usando fórmulas conhecidas. O problema é declarado, uma fórmula é identificada, as quantidades conhecidas são substituídas pela fórmula, a equação é resolvida pela desconhecida e a pergunta do problema é respondida. Normalmente, esses problemas envolvem duas equações representando duas viagens, dois investimentos, duas áreas e assim por diante. Exemplos de fórmulas incluem a área de uma região retangular,
\[A=LW \tag{2.4.2}\]
o perímetro de um retângulo,
\[P=2L+2W \tag{2.4.3}\]
e o volume de um sólido retangular,
\[V=LWH. \tag{2.4.4}\]
Quando há duas incógnitas, encontramos uma maneira de escrever uma em termos da outra porque podemos resolver apenas uma variável por vez.
Andrew precisa dirigir\(30\; min\) para o trabalho pela manhã. Ele dirige para casa usando a mesma rota, mas leva\(10\; min\) mais tempo e ele tem uma média\(10\; mi/h\) menor do que pela manhã. A que distância Andrew dirige até o trabalho?
Solução
Esse é um problema de distância, então podemos usar a fórmula\(d =rt\), em que a distância é igual à taxa multiplicada pelo tempo. Observe que quando a taxa é fornecida\(mi/h\), o tempo deve ser expresso em horas. Unidades de medida consistentes são essenciais para obter uma solução correta.
Primeiro, identificamos as quantidades conhecidas e desconhecidas. A viagem matinal de Andrew para o trabalho leva\(30\; min\), ou\(12\; h\) pelo menos, pelo menos\(r\). Sua viagem para casa leva\(40\; min\), ou\(23\; h\), e sua média de velocidade é\(10\; mi/h\) menor do que a viagem matinal. Ambas as viagens abrangem a distância\(d\). Uma tabela, como a Tabela\(\PageIndex{2}\), geralmente é útil para acompanhar as informações sobre esses tipos de problemas.
| \(d\) | \(r\) | \(t\) | |
|---|---|---|---|
| Para trabalhar | \ (d\)” style="text-align:center;” class="lt-math-1632">\(d\) | \ (r\)” style="text-align:center;” class="lt-math-1632">\(r\) | \ (t\)” style="text-align:center;” class="lt-math-1632">\(12\) |
| Para casa | \ (d\)” style="text-align:center;” class="lt-math-1632">\(d\) | \ (r\)” style="text-align:center;” class="lt-math-1632">\(r−10\) | \ (t\)” style="text-align:center;” class="lt-math-1632">\(23\) |
Escreva duas equações, uma para cada viagem.
\[d=r\left(\dfrac{1}{2}\right) \qquad \text{To work} \nonumber\]
\[d=(r-10)\left(\dfrac{2}{3}\right) \qquad \text{To home} \nonumber\]
Como as duas equações são iguais à mesma distância, nós as definimos como iguais uma à outra e resolvemos\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right )&= (r-10)\left (\dfrac{2}{3} \right )\\ \dfrac{1}{2r}&= \dfrac{2}{3}r-\dfrac{20}{3}\\ \dfrac{1}{2}r-\dfrac{2}{3}r&= -\dfrac{20}{3}\\ -\dfrac{1}{6}r&= -\dfrac{20}{3}\\ r&= -\dfrac{20}{3}(-6)\\ r&= 40 \end{align*}\]
Resolvemos a taxa de velocidade de trabalho,\(40\; mph\). Substituindo a tarifa\(40\) na viagem de ida e volta, os rendimentos\(30 mi/h\). Agora podemos responder à pergunta. Substitua a taxa novamente em qualquer equação e resolva\(d\).
\[\begin{align*}d&= 40\left (\dfrac{1}{2} \right )\\ &= 20 \end{align*}\]
A distância entre casa e trabalho é\(20\; mi\).
Análise
Observe que poderíamos ter eliminado as frações na equação multiplicando os dois lados da equação pelo LCD para resolver\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right)&= (r-10)\left (\dfrac{2}{3} \right )\\ 6\times r\left (\dfrac{1}{2} \right)&= 6\times (r-10)\left (\dfrac{2}{3} \right )\\ 3r&= 4(r-10)\\ 3r&= 4r-40\\ r&= 40 \end{align*}\]
No sábado de manhã, Jennifer precisou dirigir\(3.6\; h\) até a casa de sua mãe no fim de semana. No domingo à noite, devido ao trânsito intenso, Jennifer precisou voltar\(4\; h\) para casa. Sua velocidade era\(5\; mi/h\) mais lenta no domingo do que no sábado. Qual foi a velocidade dela no domingo?
- Responda
-
\(45\; mi/h\)
O perímetro de um pátio externo retangular é\(54\; ft\). O comprimento é\(3\; ft\) maior que a largura. Quais são as dimensões do pátio?
Solução
A fórmula do perímetro é padrão:\(P=2L+2W\). Temos duas quantidades desconhecidas, comprimento e largura. No entanto, podemos escrever o comprimento em termos de largura como\(L =W+3\). Substitua o valor do perímetro e a expressão pelo comprimento na fórmula. Muitas vezes, é útil fazer um esboço e rotular os lados como na Figura\(\PageIndex{3}\).
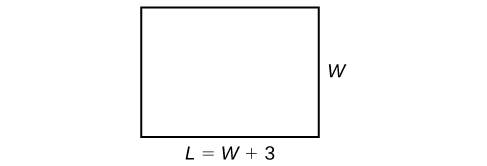
Agora podemos resolver a largura e depois calcular o comprimento.
\[\begin{align*} P&= 2L + 2W\\ 54&= 2(W+3)+2W\\ 54&= 2W+6+2W\\ 54&= 4W+6\\ 48&= 4W\\ W&= 12 \end{align*}\]
\[\begin{align*} L&= 12+3\\ L&= 15 \end{align*}\]
As dimensões são\(L = 15\; ft\)\(W = 12\; ft\) e.
Encontre as dimensões de um retângulo, considerando que o perímetro é\(110\; cm\) e o comprimento é\(1\; cm\) mais do que o dobro da largura.
- Responda
-
\(L=37\; cm\),\(W=18\; cm\)
O perímetro de um tablete de papel milimetrado é\(48\space{in.}^2\). O comprimento é\(6\; in\)... mais do que a largura. Encontre a área do papel quadriculado.
Solução
A fórmula padrão para a área é\(A =LW\); no entanto, resolveremos o problema usando a fórmula do perímetro. A razão pela qual usamos a fórmula do perímetro é porque sabemos informações suficientes sobre o perímetro que a fórmula nos permitirá resolver para uma das incógnitas. Como o perímetro e a área usam comprimento e largura como dimensões, eles geralmente são usados juntos para resolver um problema como esse.
Sabemos que o comprimento é\(6\; in\)... mais do que a largura, então podemos escrever o comprimento como\(L =W+6\). Substitua o valor do perímetro e a expressão do comprimento na fórmula do perímetro e encontre o comprimento.
\[\begin{align*} P&= 2L + 2W\\ 48&= 2(W+6)+2W\\ 48&= 2W+12+2W\\ 48&= 4W+12\\ 36&= 4W\\ W&= 9 \end{align*}\]
\[\begin{align*}L&= 9+6\\ L&= 15 \end{align*}\]
Agora, encontramos a área dadas as dimensões de\(L = 15\; in\).\(W = 9\; in\) e.
\[\begin{align*} A&= LW\\ A&=15(9)\\ A&= 135\space{in.}^2 \end{align*}\]
A área é\(135\space{in.}^2\).
Uma sala de jogos tem um perímetro de\(70\; ft\). O comprimento é cinco a mais do que o dobro da largura. Quantos\(ft^2\) tapetes novos devem ser encomendados?
- Responda
-
\(250\space{ft}^2\)
Encontre as dimensões de uma caixa de remessa, considerando que o comprimento é o dobro da largura, a altura está\(8\; \) dentro e o volume é\(1,600\space{in.}^3\).
Solução
A fórmula para o volume de uma caixa é dada como\(V =LWH\) o produto do comprimento, largura e altura. Recebemos isso\(L =2W\),\(H =8\) e. O volume é\(1,600\; \text{cubic inches}\).
\[\begin{align*} V&= LWH\\ 1600&= (2W)W(8)\\ 1600&= 16W^2\\ 100&= W^2\\ 10&= W \end{align*}\]As dimensões são\(L = 20\; in\)\(W= 10\; in\),\(H = 8\; in\) e.
Análise
Observe que a raiz quadrada de\(W^2\) resultaria em um valor positivo e um negativo. No entanto, como estamos descrevendo a largura, podemos usar somente o resultado positivo.
Acesse esses recursos on-line para obter instruções e práticas adicionais com modelos e aplicações de equações lineares.
- Resolução de problemas usando equações lineares
- Resolução de problemas usando equações
- Encontrando as dimensões da área dado o perímetro
- Encontre a distância entre as cidades usando a fórmula distância = taxa * tempo
- Aplicação de equação linear (escreva uma equação de custo)
Conceitos-chave
- Uma equação linear pode ser usada para resolver uma incógnita em um problema numérico. Veja o exemplo.
- Os aplicativos podem ser escritos como problemas matemáticos identificando quantidades conhecidas e atribuindo uma variável a quantidades desconhecidas. Veja o exemplo.
- Existem muitas fórmulas conhecidas que podem ser usadas para resolver aplicativos. Problemas de distância, por exemplo, são resolvidos usando a\(d = rt\) fórmula. Veja o exemplo.
- Muitos problemas de geometria são resolvidos usando a fórmula do perímetro\(P =2L+2W\), a fórmula\(A =LW\) da área ou a fórmula do volume\(V =LWH\). Veja exemplo, exemplo e exemplo.


