2.5: Números complexos

Last updated
Save as PDF

Page ID: 189302

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Adicione e subtraia números complexos.
Multiplique e divida números complexos.
Resolva equações quadráticas com números complexos

Descoberto por Benoit Mandelbrot por volta de 1980, o conjunto Mandelbrot é uma das imagens fractais mais reconhecíveis. A imagem é construída com base na teoria da auto-similaridade e na operação de iteração. Aumentar o zoom em uma imagem fractal traz muitas surpresas, principalmente no alto nível de repetição de detalhes que aparece à medida que a ampliação aumenta. A equação que gera essa imagem acaba sendo bastante simples.

Uma representação visual do conjunto de Mandelbrot — Figura$\PageIndex{1}$: O conjunto de Mandelbrot exibe semelhança, o que é melhor mostrado em uma animação.

Para entender melhor isso, precisamos nos familiarizar com um novo conjunto de números. Lembre-se de que o estudo da matemática se baseia continuamente em si mesmo. Os números inteiros negativos, por exemplo, preenchem um vazio deixado pelo conjunto de números inteiros positivos. O conjunto de números racionais, por sua vez, preenche um vazio deixado pelo conjunto de números inteiros. O conjunto de números reais preenche um vazio deixado pelo conjunto de números racionais. Não é de surpreender que o conjunto de números reais também tenha vazios. Nesta seção, exploraremos um conjunto de números que preenche os vazios no conjunto de números reais e descobriremos como trabalhar nele.

Expressando raízes quadradas de números negativos como múltiplos de$i$

Sabemos como encontrar a raiz quadrada de qualquer número real positivo. De forma semelhante, podemos encontrar a raiz quadrada de qualquer número negativo. A diferença é que a raiz não é real. Se o valor no radicando for negativo, diz-se que a raiz é um número imaginário. O número imaginário$i$ é definido como a raiz quadrada de$−1$.

\[\sqrt{-1}=i\]

Então, usando propriedades dos radicais,

\[i^2=(\sqrt{-1})^2=-1\]

Podemos escrever a raiz quadrada de qualquer número negativo como múltiplo de$i$. Considere a raiz quadrada de$−49$.

\[\begin{align*} \sqrt{-49}&= \sqrt{49\times(-1)}\\[4pt] &= \sqrt{49}\sqrt{-1}\\[4pt] &= 7i \end{align*}\]

Usamos$7i$ e não$−7i$ porque a raiz principal do$49$ é a raiz positiva.

Um número complexo é a soma de um número real e um número imaginário. Um número complexo é expresso na forma padrão quando escrito$a+bi$ onde$a$ está a parte real e$b$ é a parte imaginária. Por exemplo,$5+2i$ é um número complexo. Então, também é$3+4i\sqrt{3}$.

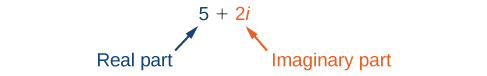
$O número complexo 5 + 2i é exibido. O 5 é rotulado como: Parte real e o 2i é rotulado como: Parte imaginária$

Os números imaginários diferem dos números reais porque um número imaginário quadrado produz um número real negativo. Lembre-se de que quando um número real positivo é quadrado, o resultado é um número real positivo e quando um número real negativo é quadrado, o resultado também é um número real positivo. Os números complexos consistem em números reais e imaginários.

Definição: NÚMEROS IMAGINÁRIOS E COMPLEXOS

Um número complexo é um número do formulário$a+bi$ em que

$a$é a parte real do número complexo.
$b$é a parte imaginária do número complexo.

Se$b=0$, então$a+bi$ é um número real. Se$a=0$ e não$b$ for igual a$0$, o número complexo é chamado de número imaginário puro. Um número imaginário é a raiz par de um número negativo.

Como fazer: Dado um número imaginário, expresse-o na forma padrão de um número complexo

Escreva$\sqrt{-a}$ como$\sqrt{a}\sqrt{-1}$.
$\sqrt{-1}$Expresse como$i$.
Escreva$\sqrt{a}\times i$ na forma mais simples.

Exemplo$\PageIndex{1}$: Expressing an Imaginary Number in Standard Form

$\sqrt{-9}$Expresse em formato padrão.

Solução

\[\begin{align*} \sqrt{-9}&= \sqrt{9}\sqrt{-1)}\\[4pt] &= 3i\\[4pt] \end{align*}\]

Na forma padrão, isso é$0+3i$.

Exercício$\PageIndex{1}$

$\sqrt{-24}$Expresse em formato padrão.

Responda: $\sqrt{-24}=0+2i\sqrt{6}$

Traçando um número complexo no plano complexo

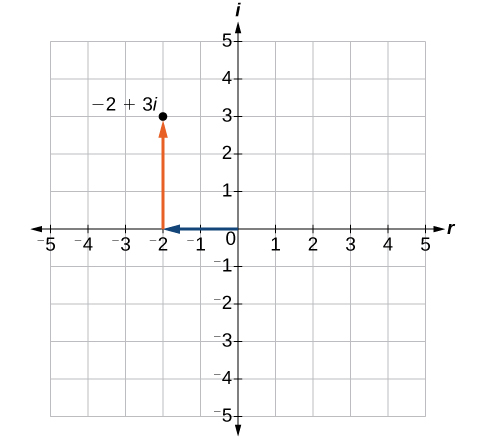
Não podemos traçar números complexos em uma reta numérica como podemos fazer com números reais. No entanto, ainda podemos representá-los graficamente. Para representar um número complexo, precisamos abordar os dois componentes do número. Usamos o plano complexo, que é um sistema de coordenadas no qual o eixo horizontal representa o componente real e o eixo vertical representa o componente imaginário. Números complexos são os pontos no plano, expressos como pares ordenados$(a,b)$, onde$a$ representa a coordenada para o eixo horizontal e$b$ representa a coordenada para o eixo vertical.

Vamos considerar o número$−2+3i$. A parte real do número complexo é$−2$ e a parte imaginária é$3$. Traçamos o par ordenado$(−2,3)$ para representar o número complexo$−2+3i$, conforme mostrado na Figura$\PageIndex{2}$.

Plano coordenado com os eixos x e y variando de menos 5 a 5. O ponto menos 2 mais 3i é plotado no gráfico. Uma seta se estende para a esquerda a partir das duas unidades de origem e, em seguida, uma seta se estende para cima três unidades a partir do final da seta anterior. — Figura$\PageIndex{2}$

PLANO COMPLEXO

No plano complexo, o eixo horizontal é o eixo real e o eixo vertical é o eixo imaginário, conforme mostrado na Figura$\PageIndex{3}$.

Um plano de coordenadas em branco com o eixo x rotulado: real e o eixo y rotulado como: imaginário. — Figura$\PageIndex{3}$

Como fazer: Dado um número complexo, represente seus componentes no plano complexo

Determine a parte real e a parte imaginária do número complexo.
Mova-se ao longo do eixo horizontal para mostrar a parte real do número.
Mova-se paralelamente ao eixo vertical para mostrar a parte imaginária do número.
Faça um gráfico do ponto.

Exemplo$\PageIndex{2}$: Plotting a Complex Number on the Complex Plane

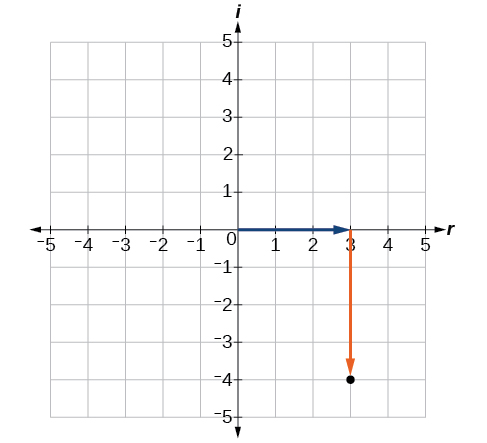
Faça um gráfico do número complexo$3−4i$ no plano complexo.

Solução

A parte real do número complexo é$3$, e a parte imaginária é$–4$. Traçamos o par ordenado$(3,−4)$ conforme mostrado na Figura$\PageIndex{4}$.

Plano coordenado com os eixos x e y variando de -5 a 5. O ponto 3 — 4i é traçado, com uma seta se estendendo para a direita a partir das 3 unidades de origem e uma seta se estendendo para baixo 4 unidades a partir do final da seta anterior. — Figura$\PageIndex{4}$

Exercício$\PageIndex{2}$

Faça um gráfico do número complexo$−4−i$ no plano complexo.

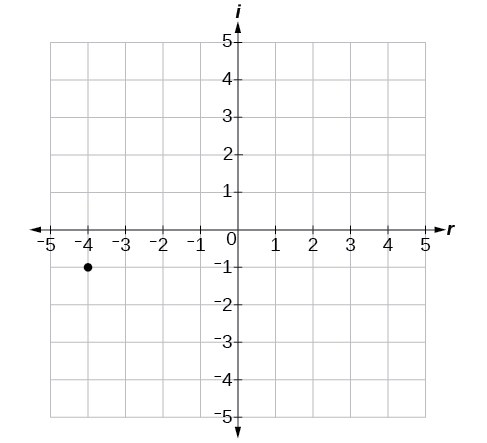
Responda: $Plano coordenado com os eixos x e y variando de menos 5 a 5. O ponto -4 i é representado graficamente.$
Figura$\PageIndex{5}$

Adicionando e subtraindo números complexos

Assim como com números reais, podemos realizar operações aritméticas em números complexos. Para somar ou subtrair números complexos, combinamos as partes reais e depois combinamos as partes imaginárias.

NÚMEROS COMPLEXOS: ADIÇÃO E SUBTRAÇÃO

Adicionando números complexos:

\[(a+bi)+(c+di)=(a+c)+(b+d)i\]

Subtração de números complexos:

\[(a+bi)−(c+di)=(a−c)+(b−d)i\]

Como fazer: Dados dois números complexos, encontre a soma ou a diferença

Identifique as partes reais e imaginárias de cada número.
Adicione ou subtraia as partes reais.
Adicione ou subtraia as partes imaginárias.

Exemplo$\PageIndex{3}$: Adding and Subtracting Complex Numbers

Adicione ou subtraia conforme indicado.

$(3−4i)+(2+5i)$
$(−5+7i)−(−11+2i)$

Solução

\[\begin{align*} (3-4i)+(2+5i)&= 3-4i+2+5i\\[4pt] &= 3+2+(-4i)+5i\\[4pt] &= (3+2)+(-4+5)i\\[4pt] &= 5+i \end{align*}\]
\[\begin{align*} (-5+7i)-(-11+2i)&= -5+7i+11-2i\\[4pt] &= -5+11+7i-2i\\[4pt] &= (-5+11)+(7-2)i\\[4pt] &= 6+5i \end{align*}\]

Exercício$\PageIndex{3}$

Subtraia$2+5i$ de$3–4i$.

Responda: $(3−4i)−(2+5i)=1−9i$

Multiplicação de números complexos

Multiplicar números complexos é muito parecido com multiplicar binômios. A principal diferença é que trabalhamos com as partes real e imaginária separadamente.

Multiplicação de um número complexo por um número real

Vamos começar multiplicando um número complexo por um número real. Distribuímos o número real da mesma forma que faríamos com um binômio. Considere, por exemplo,$3(6+2i)$:

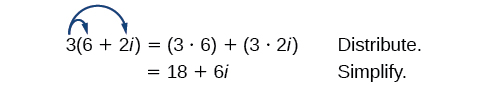
$Multiplicação de um número real e um número complexo. O 3 fora dos parênteses tem setas que se estendem dele até o 6 e o 2i dentro dos parênteses. Essa expressão é definida como igual à quantidade três vezes seis mais a quantidade três vezes duas vezes i; essa é a propriedade distributiva. A próxima linha é igual a dezoito mais seis vezes i; a simplificação.$

Como fazer: Dado um número complexo e um número real, multiplique para encontrar o produto

Use a propriedade distributiva.
Simplifique.

Exemplo$\PageIndex{4}$: Multiplying a Complex Number by a Real Number

Encontre o produto$4(2+5i)$.

Solução

Distribua$4$ o.

\[\begin{align*} 4(2+5i)&= (4\cdot 2)+(4\cdot 5i)\\[4pt] &= 8+20i \end{align*}\]

Exercício$\PageIndex{4}$

Encontre o produto:$\dfrac{1}{2}(5−2i)$.

Responda: $\dfrac{5}{2}-i$

Multiplicação de números complexos

Agora, vamos multiplicar dois números complexos. Podemos usar a propriedade distributiva ou, mais especificamente, o método FOIL porque estamos lidando com binômios. Lembre-se de que FOIL é um acrônimo para multiplicar os termos Primeiro, Interno, Externo e Último. A diferença com números complexos é que quando obtemos um termo quadrado$i^2$,, ele é igual$-1$.

\[\begin{align*} (a+bi)(c+di)&= ac+adi+bci+bdi^2\\[4pt] &= ac+adi+bci-bd(-1)\qquad i^2 = -1\\[4pt] &= ac+adi+bci-bd\\[4pt] &= (ac-bd)+(ad+bc)i \end{align*}\]

Agrupe termos reais e termos imaginários.

Como fazer: Dados dois números complexos, multiplique para encontrar o produto

Use a propriedade distributiva ou o método FOIL.
Lembre-se disso$i^2=-1$.
Agrupe os termos reais e os termos imaginários

Exemplo$\PageIndex{5}$: Multiplying a Complex Number by a Complex Number

Multiplique$(4+3i)(2−5i)$.

Solução

\[\begin{align*} (4+3i)(2-5i)&= 4(2)-4(5i)+3i(2)-(3i)(5i)\\[4pt] &= 8-20i+6i-15(i^2)\\[4pt] &= (8+15)+(-20+6)i\\[4pt] &= 23-14i \end{align*}\]

Exercício$\PageIndex{5}$

Multiplique:$(3−4i)(2+3i)$.

Responda: $18+i$

Dividindo números complexos

Dividir dois números complexos é mais complicado do que somar, subtrair ou multiplicar porque não podemos dividir por um número imaginário, o que significa que qualquer fração deve ter um denominador de número real para escrever a resposta na forma padrão$a+bi$. Precisamos encontrar um termo pelo qual possamos multiplicar o numerador e o denominador que eliminará a porção imaginária do denominador para que acabemos com um número real como denominador. Esse termo é chamado de conjugado complexo do denominador, que é encontrado alterando o sinal da parte imaginária do número complexo. Em outras palavras, o complexo conjugado de$a+bi$ é$a−bi$. Por exemplo, o produto de$a+bi$ e$a−bi$ é

\[\begin{align*} (a+bi)(a-bi)&= a^2-abi+abi-b^2i^2\\[4pt] &= a^2+b^2 \end{align*}\]

O resultado é um número real.

Observe que os conjugados complexos têm uma relação oposta: o conjugado complexo de$a+bi$ é$a−bi$ e o conjugado complexo de$a−bi$ é$a+bi$. Além disso, quando uma equação quadrática com coeficientes reais tem soluções complexas, as soluções são sempre conjugadas complexas umas das outras.

Suponha que queiramos dividir$c+di$ por$a+bi$, onde$a$ nem$b$ é igual a zero. Primeiro escrevemos a divisão como uma fração, depois encontramos o conjugado complexo do denominador e multiplicamos.

$\dfrac{c+di}{a+bi}$onde$a≠0$ e$b≠0$

Multiplique o numerador e o denominador pelo conjugado complexo do denominador.

\[\begin{align*} \dfrac{(c+di)}{(a+bi)}\cdot \dfrac{(a-bi)}{(a-bi)}&= \dfrac{(c+di)(a-bi)}{(a+bi)(a-bi)}\\[4pt] &= \dfrac{ca-cbi+adi-bdi^2}{a^2-abi+abi-b^2i^2} \qquad \text{Apply the distributive property}\\[4pt] &= \dfrac{ca-cbi+adi-bd(-1)}{a^2-abi+abi-b^2(-1)} \qquad \text{Simplify, remembering that } i^2=-1\\[4pt] &= \dfrac{(ca+bd)+(ad-cb)i}{a^2+b^2} \end{align*}\]

Definição: O COMPLEXO CONJUGADO

O conjugado complexo de um número complexo$a+bi$ é$a−bi$. É encontrado alterando o sinal da parte imaginária do número complexo. A parte real do número permanece inalterada.

Quando um número complexo é multiplicado por seu conjugado complexo, o resultado é um número real.
Quando um número complexo é adicionado ao seu conjugado complexo, o resultado é um número real.

Exemplo$\PageIndex{6}$: Finding Complex Conjugates

Encontre o conjugado complexo de cada número.

$2+i\sqrt{5}$
$-\dfrac{1}{2}i$

Solução

O número já está no formulário$a+bi$. O conjugado complexo é$a−bi$, ou$2−i\sqrt{5}$.
Podemos reescrever esse número no formulário$a+bi$ como$0−\dfrac{1}{2}i$. O conjugado complexo é$a−bi$, ou$0+\dfrac{1}{2}i$. Isso pode ser escrito simplesmente como$\dfrac{1}{2}i$.

Análise

Embora tenhamos visto que podemos encontrar o conjugado complexo de um número imaginário, na prática geralmente encontramos os conjugados complexos apenas de números complexos com um componente real e um componente imaginário. Para obter um número real de um número imaginário, podemos simplesmente multiplicar por$i$.

Exercício$\PageIndex{6}$

Encontre o conjugado complexo de$−3+4i$.

Responda: $−3−4i$

Como: Dados dois números complexos, divida um pelo outro

Escreva o problema da divisão como uma fração.
Determine o conjugado complexo do denominador.
Multiplique o numerador e o denominador da fração pelo conjugado complexo do denominador.
Simplifique.

Exemplo$\PageIndex{7}$: Dividing Complex Numbers

Divida$(2+5i)$ por$(4−i)$.

Solução

Começamos escrevendo o problema como uma fração.

\[\dfrac{(2+5i)}{(4−i)} \nonumber \]

Em seguida, multiplicamos o numerador e o denominador pelo conjugado complexo do denominador.

\[\dfrac{(2+5i)}{(4−i)}⋅\dfrac{(4+i)}{(4+i)} \nonumber \]

Para multiplicar dois números complexos, expandimos o produto da mesma forma que faríamos com polinômios (usando FOIL).

\[\begin{align*} \dfrac{(2+5i)}{(4-i)}\cdot \dfrac{(4+i)}{(4+i)}&= \dfrac{8+2i+20i+5i^2}{16+4i-4i-i^2}\\[4pt] &= \dfrac{8+2i+20i+5(-1)}{16+4i-4i-(-1)}\; i^2=-1 \\[4pt] &= \dfrac{3+22i}{17}\\[4pt] &= \dfrac{3}{17}+\dfrac{22}{17i} \end{align*}\]

Separe as partes reais e imaginárias.

Observe que isso expressa o quociente na forma padrão.

Simplificando os poderes do$i$

Os poderes do$i$ são cíclicos. Vamos ver o que acontece quando aumentamos$i$ para poderes crescentes.

\[i^1=i \nonumber \]\[i^2=-1 \nonumber \]\[i^3=i^2⋅i=-1⋅i=-i \nonumber \]\[i^4=i^3⋅i=-i⋅i=-i^2=-(-1)=1 \nonumber \]\[i^5=i^4⋅i=1⋅i=i \nonumber \]

Podemos ver que quando chegamos à quinta potência de i, ela é igual à primeira potência. À medida que continuamos a multiplicar$i$ aumentando os poderes, veremos um ciclo de quatro. Vamos examinar os próximos quatro poderes do$i$.

\[i^6=i^5⋅i=i⋅i=i^2=-1 \nonumber \]\[i^7=i^6⋅i=i^2⋅i=i^3=-i \nonumber \]\[i^8=i^7⋅i=i^3⋅i=i^4=1 \nonumber \]\[i^9=i^8⋅i=i^4⋅i=i^5=i \nonumber \]

O ciclo se repete continuamente: a$i,−1,−i,1,$ cada quatro potências.

Exemplo$\PageIndex{8}$: Simplifying Powers of $i$

Avalie:$i^{35}$.

Solução

Desde então$i^4=1$, podemos simplificar o problema considerando o maior número$i^4$ possível de fatores. Para fazer isso, primeiro determine quantas vezes$4$ entra$35: 35=4⋅8+3$.

\[i^{35}=i^{4⋅8+3}=i^{4⋅8}⋅i^3={(i^4)}^8⋅i^3=i^8⋅i^3=i^3=−i \nonumber \]

Exercício$\PageIndex{7}$

Avalie:$i^{18}$

Responda: $−1$

PERGUNTAS E RESPOSTAS

Podemos escrever$i^{35}$ de outras formas úteis?

Como vimos no Exemplo$\PageIndex{8}$, reduzimos$i^{35}$ para$i^3$ dividindo o expoente$4$ e usando o restante para encontrar a forma simplificada. Mas talvez outra fatoração de$i^{35}$ possa ser mais útil. A tabela$\PageIndex{1}$ mostra algumas outras fatorizações possíveis.

Tabela$\PageIndex{1}$
Fatoração de$i^{35}$	$i^{34}⋅i$	$i^{33}⋅i^2$	$i^{31}⋅i^4$	$i^{19}⋅i^{16}$
Forma reduzida	${(i^2)}^{17}⋅i$	$i^{33}⋅(−1)$	$i^{31}⋅1$	$i^{19}⋅{(i^4)}^4$
Formulário simplificado	${(−1)}^{17}⋅i$	$−i^{33}$	$i^{31}$	$i^{19}$

Cada uma delas acabará resultando na resposta que obtivemos acima, mas pode exigir várias etapas a mais do que nosso método anterior.

Mídia

Acesse esses recursos on-line para obter instruções e práticas adicionais com números complexos.

Adicionando e subtraindo números complexos
Multiplique números complexos
Multiplicação de conjugados complexos
Elevando você a dois poderes

Conceitos-chave

A raiz quadrada de qualquer número negativo pode ser escrita como múltiplo de $i$. Veja o exemplo.
Para traçar um número complexo, usamos duas linhas numéricas, cruzadas para formar o plano complexo. O eixo horizontal é o eixo real e o eixo vertical é o eixo imaginário. Veja o exemplo.
Números complexos podem ser somados e subtraídos combinando as partes reais e combinando as partes imaginárias. Veja o exemplo.
Números complexos podem ser multiplicados e divididos.
- Para multiplicar números complexos, distribua da mesma forma que ocorre com os polinômios. Veja o exemplo e o exemplo.
- Para dividir números complexos, multiplique o numerador e o denominador pelo conjugado complexo do denominador para eliminar o número complexo do denominador. Veja o exemplo e o exemplo.
Os poderes do i são cíclicos, repetindo-se a cada quatro. Veja o exemplo.

Fatoração de\(i^{35}\)	\(i^{34}⋅i\)	\(i^{33}⋅i^2\)	\(i^{31}⋅i^4\)	\(i^{19}⋅i^{16}\)
Forma reduzida	\({(i^2)}^{17}⋅i\)	\(i^{33}⋅(−1)\)	\(i^{31}⋅1\)	\(i^{19}⋅{(i^4)}^4\)
Formulário simplificado	\({(−1)}^{17}⋅i\)	\(−i^{33}\)	\(i^{31}\)	\(i^{19}\)

Definição: NÚMEROS IMAGINÁRIOS E COMPLEXOS

Como fazer: Dado um número imaginário, expresse-o na forma padrão de um número complexo

Exemplo\(\PageIndex{1}\): Expressing an Imaginary Number in Standard Form

Exercício\(\PageIndex{1}\)