2.6: Equações quadráticas

Objetivos de

• Resolva equações quadráticas por fatoração.
• Resolva equações quadráticas pela propriedade da raiz quadrada.
• Resolva equações quadráticas completando o quadrado.
• Resolva equações quadráticas usando a fórmula quadrática.

O monitor do computador à esquerda na Figura$\PageIndex{1}$ é um modelo de$23.6$ -polegadas e o da direita é um modelo de$27$ -polegadas. Proporcionalmente, os monitores parecem muito parecidos. Se houver uma quantidade limitada de espaço e desejarmos o maior monitor possível, como decidimos qual deles escolher? Nesta seção, aprenderemos como resolver problemas como esse usando quatro métodos diferentes.

Figura$\PageIndex{1}$

Resolvendo equações quadráticas por fatoração

Uma equação contendo um polinômio de segundo grau é chamada de equação quadrática. Por exemplo, equações como$2x^2 +3x−1=0$ e$x^2−4= 0$ são equações quadráticas. Eles são usados de inúmeras maneiras nas áreas de engenharia, arquitetura, finanças, ciências biológicas e, claro, matemática.

Muitas vezes, o método mais fácil de resolver uma equação quadrática é fatorar. Fatorar significa encontrar expressões que podem ser multiplicadas juntas para dar a expressão em um lado da equação.

Se uma equação quadrática puder ser fatorada, ela será escrita como um produto de termos lineares. A resolução por fatoração depende da propriedade do produto zero, que afirma que se$a⋅b=0$, então$a = 0$ ou$b =0$, onde a e b são números reais ou expressões algébricas. Em outras palavras, se o produto de dois números ou duas expressões for igual a zero, um dos números ou uma das expressões deverá ser igual a zero porque zero multiplicado por qualquer coisa é igual a zero.

A multiplicação dos fatores expande a equação para uma sequência de termos separados por sinais de mais ou menos. Então, nesse sentido, a operação de multiplicação desfaz a operação de fatoração. Por exemplo, expanda a expressão fatorada$(x−2)(x+3)$ multiplicando os dois fatores juntos.

$$\begin{align*} (x-2)(x+3)&= x^2+3x-2x-6\\ &= x^2+x-6\\ \end{align*}$$

O produto é uma expressão quadrática. Definido igual a zero,$x^2+x−6= 0$ é uma equação quadrática. Se fôssemos fatorar a equação, recuperaríamos os fatores que multiplicamos.

O processo de fatorar uma equação quadrática depende do coeficiente principal, seja ele$1$ ou outro inteiro. Examinaremos as duas situações; mas primeiro, queremos confirmar que a equação está escrita na forma padrão$ax^2+bx+c=0$, onde$a$$b$, e$c$ são números reais,$a≠0$ e. A equação$x^2 +x−6= 0$ está na forma padrão.

Podemos usar a propriedade de produto zero para resolver equações quadráticas nas quais primeiro precisamos fatorar o maior fator comum (GCF) e para equações que também têm fórmulas de fatoração especiais, como a diferença dos quadrados, que veremos mais adiante nesta seção.

PROPRIEDADE DE PRODUTO ZERO E EQUAÇÕES QUADRÁTICAS

Os estados da propriedade de produto zero

Se$a⋅b=0$, então$a=0$ ou$b=0$,

onde$a$ e$b$ são números reais ou expressões algébricas.

Uma equação quadrática é uma equação contendo um polinômio de segundo grau; por exemplo

$$ax^2+bx+c=0$$

onde$a$$b$, e$c$ são números reais e, se$a≠0$, estão na forma padrão.

Resolvendo quadráticas com um coeficiente principal de$1$

Na equação quadrática$x^2 +x−6=0$, o coeficiente principal, ou o coeficiente de$x^2$, é$1$. Temos um método para fatorar equações quadráticas nesta forma.

Como: Fatorar uma equação quadrática com o coeficiente principal de 1

1. Encontre dois números cujo produto seja igual$c$ e cuja soma seja igual$b$.
2. Use esses números para escrever dois fatores da forma$(x+k)$ ou$(x−k)$, onde k é um dos números encontrados na etapa 1. Use os números exatamente como estão. Em outras palavras, se os dois números forem$1$ e$−2$, os fatores são$(x+1)(x−2)$.
3. Resolva usando a propriedade de produto zero definindo cada fator igual a zero e resolvendo para a variável.

Exemplo$\PageIndex{1}$: Solving a Quadratic with Leading Coefficient of $1$

Fatore e resolva a equação:$x^2+x−6=0$.

Solução

Para fatorar$x^2 +x−6=0$, procuramos dois números cujo produto seja igual$−6$ e cuja soma seja igual$1$. Comece examinando os possíveis fatores de$−6$.

$$1⋅(−6) \nonumber$$

$$(−6)⋅1 \nonumber$$

$$2⋅(−3) \nonumber$$

$$3⋅(−2) \nonumber$$

O último par,$3⋅(−2)$ somado a$1$, então esses são os números. Observe que apenas um par de números funcionará. Em seguida, escreva os fatores.

$$(x−2)(x+3)=0 \nonumber$$

Para resolver essa equação, usamos a propriedade de produto zero. Defina cada fator igual a zero e resolva.

$$\begin{align*} (x-2)(x+3)&= 0\\ (x-2)&= 0\\ x&= 2\\ (x+3)&= 0\\ x&= -3 \end{align*}$$

As duas soluções são$2$$−3$ e. Podemos ver como as soluções se relacionam com o gráfico na Figura$\PageIndex{2}$. As soluções são as interceptações x de$x^2 +x−6=0$.

Figura$\PageIndex{2}$

Exercício$\PageIndex{1}$

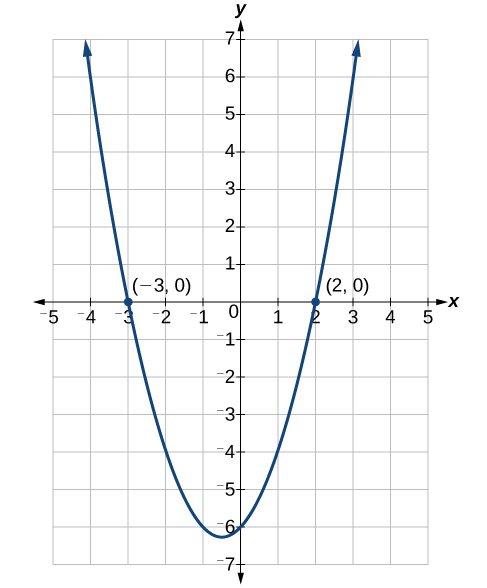
Fatore e resolva a equação quadrática:$x^2−5x−6=0$.

Resposta

$(x−6)(x+1)=0$,$x=6$,$x=−1$

Exemplo$\PageIndex{2}$: Solve the Quadratic Equation by Factoring

Resolva a equação quadrática fatorando:$x^2+8x+15=0$.

Solução

Encontre dois números cujo produto seja igual$15$ e cuja soma seja igual$8$. Liste os fatores de$15$.

$$1⋅15 \nonumber$$

$$3⋅5 \nonumber$$

$$(−1)⋅(−15) \nonumber$$

$$(−3)⋅(−5) \nonumber$$

Os números somados$8$ são$3$$5$ e. Em seguida, escreva os fatores, defina cada fator igual a zero e resolva.

$$\begin{align*} (x+3)(x+5)&= 0\\ (x+3)&= 0\\ x&= -3\\ (x+5)&= 0\\ x&= -5 \end{align*}$$

As soluções são$−3$$−5$ e.

Exercício$\PageIndex{2}$

Resolva a equação quadrática fatorando:$x^2−4x−21=0$.

Resposta

$(x−7)(x+3)=0$,$x=7$,$x=−3$

Exemplo$\PageIndex{3}$: Using Zero-Product Property to Solve a Quadratic Equation

Resolva a equação da diferença dos quadrados usando a propriedade de produto zero:$x^2−9=0$.

Solução

Reconhecendo que a equação representa a diferença dos quadrados, podemos escrever os dois fatores tomando a raiz quadrada de cada termo, usando um sinal de menos como operador em um fator e um sinal de mais como operador no outro. Resolva usando a propriedade de fator zero.

$$\begin{align*} x^2-9&= 0\\ (x-3)(x+3)&= 0\\ x-3&= 0\\ x&= 3\\ (x+3)&= 0\\ x&= -3 \end{align*}$$

As soluções são$3$$−3$ e.

Exercício$\PageIndex{3}$

Resolva fatorando:$x^2−25=0$.

Resposta

$(x+5)(x−5)=0, x=−5, x=5$

Fatorando e resolvendo uma equação quadrática de ordem superior

Quando o coeficiente principal não é$1$, fatoramos uma equação quadrática usando o método chamado agrupamento, que requer quatro termos.

Agrupamento: Etapas para fatorar equações quadráticas

Com a equação na forma padrão, vamos revisar os procedimentos de agrupamento

1. Com o quadrático na forma padrão$ax^2+bx+c=0$, multiplique$a⋅c$.
2. Encontre dois números cujo produto seja igual a ac e cuja soma seja igual$b$.
3. Reescreva a equação substituindo o$bx$ termo por dois termos usando os números encontrados na etapa$1$ como coeficientes de$x$.
4. Fator os dois primeiros termos e depois fatore os dois últimos termos. As expressões entre parênteses devem ser exatamente as mesmas para usar o agrupamento.
5. Considere a expressão entre parênteses.
6. Defina as expressões como iguais a zero e resolva a variável.

Exemplo$\PageIndex{4}$: Solving a Quadratic Equation Using Grouping

Use o agrupamento para fatorar e resolver a equação quadrática:$4x^2+15x+9=0$.

Solução

Primeiro, multiplique$ac:4(9)=36$. Em seguida, liste os fatores de$36$.

$$1⋅36 \nonumber$$

$$2⋅18 \nonumber$$

$$3⋅12 \nonumber$$

$$4⋅9 \nonumber$$

$$6⋅6 \nonumber$$

O único par de fatores que somam$15$ é$3+12$. Reescreva a equação substituindo o termo b$15x$,, por dois termos usando$3$ e$12$ como coeficientes de$x$. Fator os dois primeiros termos e depois fatore os dois últimos termos.

$$\begin{align*} 4x^2+3x+12x+9&= 0\\ x(4x+3)+3(4x+3)&= 0\\ (4x+3)(x+3)&= 0 \qquad \text{Solve using the zero-product property}\\ (4x+3)&= 3\\ x&= -\dfrac{3}{4}\\ (x+3)&= 0\\ x&= -3 \end{align*}$$

As soluções são$−\dfrac{3}{4}$,$−3$ e. Veja a Figura$\PageIndex{3}$.

Figura$\PageIndex{3}$

Exercício$\PageIndex{4}$

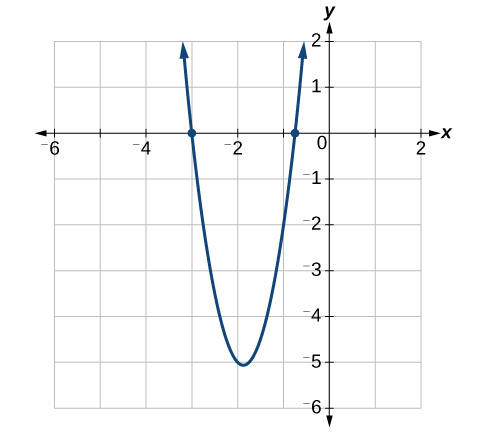
Resolva usando fatoração por agrupamento:$12x^2+11x+2=0$.

Resposta

$(3x+2)(4x+1)=0$,$x=−\dfrac{2}{3}$,$x=−\dfrac{1}{4}$

Exemplo$\PageIndex{5}$: Solving a Higher Degree Quadratic Equation by Factoring

Resolva a equação fatorando:$−3x^3−5x^2−2x=0$.

Solução

Essa equação não parece quadrática, pois a maior potência não é$3$$2$. Lembre-se de que a primeira coisa que queremos fazer ao resolver qualquer equação é considerar o GCF, se houver. E isso acontece aqui. Podemos considerar todos os termos e, em seguida, prosseguir com o agrupamento.$−x$

\ [\ begin {align*}
-3x^3-5x^2-2x&= 0\\
-x (3x^2+5x+2) &= 0\\
-x (3x^2+3x+2x+2) &= 0\ qquad\ text {Use o agrupamento na expressão entre parênteses}\\
-x [3x (x+1) +2 (x+1)] &= 0\\
-x (3x+2) (x+1) &= 0\
\\ text {Agora, usamos a propriedade do produto zero. Observe que temos três fatores.} \\
-x&= 0\\
x&= 0\\
3x+2&= 0\\
x&= -\ dfrac {2} {3}\\
x+1&= 0\\
x&= -1
\ end {align*}\]

As soluções são$0$$−\dfrac{2}{3}$,$−1$ e.

Exercício$\PageIndex{5}$

Resolva fatorando:$x^3+11x^2+10x=0$.

Resposta

$x=0, x=−10, x=−1$

Usando a propriedade de raiz quadrada

Quando não há um termo linear na equação, outro método para resolver uma equação quadrática é usando a propriedade raiz quadrada, na qual isolamos o$x^2$ termo e pegamos a raiz quadrada do número do outro lado do sinal de igual. Lembre-se de que às vezes podemos ter que manipular a equação para isolar o$x^2$ termo para que a propriedade da raiz quadrada possa ser usada.

A PROPRIEDADE DA RAIZ QUADRADA

Com o$x^2$ termo isolado, a propriedade da raiz quadrada afirma que:

se$x^2=k$, então$x=±\sqrt{k}$

onde$k$ é um número real diferente de zero.

Como fazer: Dada uma equação quadrática com um$x^2$ term but no $x$ term, use the square root property to solve it

1. Isole o$x^2$ termo em um lado do sinal de igual.
2. Pegue a raiz quadrada dos dois lados da equação, colocando um$±$ sinal antes da expressão no lado oposto ao termo quadrado.
3. Simplifique os números na lateral com o$±$ sinal.

Exemplo$\PageIndex{6}$: Solving a Simple Quadratic Equation Using the Square Root Property

Resolva a quadrática usando a propriedade de raiz quadrada:$x^2=8$.

Solução

Pegue a raiz quadrada dos dois lados e depois simplifique o radical. Lembre-se de usar um$±$ sinal antes do símbolo radical.

$$\begin{align*} x^2&= 8\\ x&= \pm \sqrt{8}\\ &= \pm 2\sqrt{2} \end{align*}$$

As soluções são$2\sqrt{2}$,$-2\sqrt{2}$

Exemplo$\PageIndex{7}$: Solving a Quadratic Equation Using the Square Root Property

Resolva a equação quadrática:$4x^2+1=7$.

Solução

Primeiro, isole o$x^2$ termo. Em seguida, pegue a raiz quadrada dos dois lados.

$$\begin{align*} 4x^2+1&= 7\\ 4x^2&= 6\\ x^2&= \dfrac{6}{4}\\ x&= \pm \dfrac{\sqrt{6}}{2} \end{align*}$$

As soluções são$\dfrac{\sqrt{6}}{2}$,$-\dfrac{\sqrt{6}}{2}$ e.

Exercício$\PageIndex{6}$

Resolva a equação quadrática usando a propriedade da raiz quadrada:$3{(x−4)}^2=15$.

Resposta

$x=4±\sqrt{5}$

Completando a Praça

Nem todas as equações quadráticas podem ser fatoradas ou resolvidas em sua forma original usando a propriedade raiz quadrada. Nesses casos, podemos usar um método para resolver uma equação quadrática conhecida como completar o quadrado. Usando esse método, adicionamos ou subtraímos termos em ambos os lados da equação até termos um trinômio quadrado perfeito em um lado do sinal de igual. Em seguida, aplicamos a propriedade raiz quadrada. Para completar o quadrado, o coeficiente principal,$a$, deve ser igual$1$. Se isso não acontecer, divida a equação inteira por$a$. Em seguida, podemos usar os procedimentos a seguir para resolver uma equação quadrática completando o quadrado.

Usaremos o exemplo$x^2+4x+1=0$ para ilustrar cada etapa.

Dada uma equação quadrática que não pode ser fatorada, e com$a=1$, first add or subtract the constant term to the right sign of the equal sign.

\ [\ begin {align*}
x^2+4x+1&= 0\\
x^2+4x&= -1\ qquad\ text {Multiplique o termo b}\ text {por}\ dfrac {1} {2}\ text {e quadre-o.} \\
\ dfrac {1} {2} (4) &= 2\\
2^2&= 4\ qquad\ text {Add}\ left ({\ dfrac {1} {2}}\ right) ^2\ text {em ambos os lados do sinal de igual e simplifique o lado direito. Temos}\\
x^2+4x+4&= -1+4\\
x^2+4x+4&= 3\ qquad\ text {O lado esquerdo da equação agora pode ser fatorado como um quadrado perfeito.} \\
{(x+2)} ^2&=3\\
\ sqrt {{(x+2)} ^2} &=\ pm\ sqrt {3}\ qquad\ text {Use a propriedade da raiz quadrada e resolva.} \\
\ sqrt {{(x+2)} ^2} &=\ pm\ sqrt {3}\\
x+2&=\ pm\ sqrt {3}\\
x&= -2\ pm\ sqrt {3}
\ end {align*}\]

As soluções são$−2+\sqrt{3}$,$−2−\sqrt{3}$ e.

Exemplo$\PageIndex{8}$: Solving a Quadratic by Completing the Square

Resolva a equação quadrática completando o quadrado:$x^2−3x−5=0$.

Solução

Primeiro, mova o termo constante para o lado direito do sinal de igual.

\ [\ begin {align*}
x^2-3x&= 5\ qquad\ text {Então, pegue}\ dfrac {1} {2}\ text {do termo b e coloque-o ao quadrado.} \\
\ dfrac {1} {2} (-3) &= -\ dfrac {3} {2}\\
{\ left (-\ dfrac {3} {2}\ direita)} ^2=\ dfrac {9} {4}\
x^2-3x+ {\ left (-\ dfrac {3} {2}\ direita)} ^2&= 5+ {\ left (-\ dfrac {3} {2}\ right)} ^2\ qquad\ text {Adicione o resultado aos dois lados do sinal de igual.} \\
x^2-3x+\ dfrac {9} {4} &= 5+\ dfrac {9} {4}\
\ text {Considere o lado esquerdo como um quadrado perfeito e simplifique o lado direito.} \\
{\ left (x-\ dfrac {3} {2}\ right)} ^2&=\ dfrac {29} {4}\\
(x-\ dfrac {3} {2}) &=\ pm\ dfrac {\ sqrt {29}} {2}\ qquad\ text {Use a propriedade da raiz quadrada e resolva.} \\
x&=\ dfrac {3} {2}\ pm\ dfrac {\ sqrt {29}} {2}\
\ end {align*}\]

As soluções são$\dfrac{3}{2}+\dfrac{\sqrt{29}}{2}$, e$\dfrac{3}{2}-\dfrac{\sqrt{29}}{2}$

Exercício$\PageIndex{7}$

Resolva completando o quadrado:$x^2−6x=13$.

Resposta

$x=3±\sqrt{22}$

Usando a fórmula quadrática

O quarto método para resolver uma equação quadrática é usando a fórmula quadrática, uma fórmula que resolverá todas as equações quadráticas. Embora a fórmula quadrática funcione em qualquer equação quadrática na forma padrão, é fácil cometer erros ao substituir os valores na fórmula. Preste muita atenção ao substituir e use parênteses ao inserir um número negativo.

Podemos derivar a fórmula quadrática completando o quadrado. Vamos assumir que o coeficiente principal é positivo; se for negativo, podemos multiplicar a equação por$−1$ e obter um positivo a. Dado$ax^2+bx+c=0, a≠0$, completaremos o quadrado da seguinte forma:

Primeiro, mova o termo constante para o lado direito do sinal de igual:

$$ax^2+bx=−c \nonumber$$

Como queremos que o coeficiente principal seja igual$1$, divida por$a$:

$$x^2+\dfrac{b}{a}x=−\dfrac{c}{a} \nonumber$$

Em seguida, encontre$\dfrac{1}{2}$ o termo intermediário e adicione${(\dfrac{1}{2}\dfrac{b}{a})}^2=\dfrac{b^2}{4a^2}$ aos dois lados do sinal de igual:

$$x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}=\dfrac{b^2}{4a^2}-\dfrac{c}{a} \nonumber$$

Em seguida, escreva o lado esquerdo como um quadrado perfeito. Encontre o denominador comum do lado direito e escreva-o como uma única fração:

$${(x+\dfrac{b}{2a})}^2=\dfrac{b^2-4ac}{4a^2} \nonumber$$

Agora, use a propriedade de raiz quadrada, que fornece

$$x+\dfrac{b}{2a}=±\sqrt{\dfrac{b^2-4ac}{4a^2}} \nonumber$$

$$x+\dfrac{b}{2a}=\dfrac{±\sqrt{b^2-4ac}}{2a} \nonumber$$

Finalmente, adicione$-\dfrac{b}{2a}$ os dois lados da equação e combine os termos no lado direito. Assim,

$$x=\dfrac{-b±\sqrt{b^2-4ac}}{2a} \nonumber$$

A FÓRMULA QUADRÁTICA

Escrita na forma padrão$ax^2+bx+c=0$, qualquer equação quadrática pode ser resolvida usando a fórmula quadrática:

$$x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}$$

onde$a$$b$, e$c$ são números reais$a≠0$ e.

Como

Dada uma equação quadrática, resolva-a usando a fórmula quadrática

1. Certifique-se de que a equação esteja na forma padrão:$ax^2+bx+c=0$.
2. Anote os valores dos coeficientes e do termo constante$a$$b$,,$c$ e.
3. Substitua cuidadosamente os valores anotados na etapa 2 na equação. Para evitar erros desnecessários, use parênteses ao redor de cada entrada de número na fórmula.
4. Calcule e resolva.

Exemplo$\PageIndex{9}$: Solve the Quadratic Equation Using the Quadratic Formula

Resolva a equação quadrática:$x^2+5x+1=0$.

Solução

Identifique os coeficientes:$a=1,b=5,c=1$. Em seguida, use a fórmula quadrática.

$$\begin{align*} x&= \dfrac{-(5) \pm \sqrt{(5)^2-4(1)(1)}}{2(1)}\\ &= \dfrac{-5 \pm \sqrt{25-4}}{2}\\ &= \dfrac{-5 \pm \sqrt{21}}{2} \end{align*}$$

Exemplo$\PageIndex{10}$: Solving a Quadratic Equation with the Quadratic Formula

Use a fórmula quadrática para resolver$x^2+x+2=0$.

Solução

Primeiro, identificamos os coeficientes:$a=1$$b=1$,$c=2$ e.

Substitua esses valores na fórmula quadrática.

$$\begin{align*} x&= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\ &= \dfrac{-(1) \pm \sqrt{(1)^2-4(1)(2)}}{2(1)}\\ &= \dfrac{-1 \pm \sqrt{1-8}}{2}\\ &= \dfrac{-1 \pm \sqrt{-7}}{2}\\ &= \dfrac{-1 \pm i\sqrt{7}}{2} \end{align*}$$

Exercício$\PageIndex{8}$

Resolva a equação quadrática usando a fórmula quadrática:$9x^2+3x−2=0$.

Resposta

$x=-\dfrac{2}{3},x=\dfrac{1}{3}$

O discriminante

A fórmula quadrática não apenas gera as soluções para uma equação quadrática, ela nos fala sobre a natureza das soluções quando consideramos o discriminante, ou a expressão sob o radical$b^2−4ac$. O discriminante nos diz se as soluções são números reais ou números complexos e quantas soluções de cada tipo esperar. A tabela$\PageIndex{1}$ relaciona o valor do discriminante às soluções de uma equação quadrática.

Tabela$\PageIndex{1}$

Valor do discriminante	Resultados
$b^2−4ac=0$	Uma solução racional (solução dupla)
$b^2−4ac>0$, quadrado perfeito	Duas soluções racionais
$b^2−4ac>0$, não é um quadrado perfeito	Duas soluções irracionais
$b^2−4ac<0$	Duas soluções complexas

O DISCRIMINANTE

Para$ax^2+bx+c=0$, onde$a$,$b$, e$c$ são números reais, o discriminante é a expressão sob o radical na fórmula quadrática:$b^2−4ac$. Ele nos diz se as soluções são números reais ou números complexos e quantas soluções de cada tipo esperar.

Exemplo$\PageIndex{11}$: Using the Discriminant to Find the Nature of the Solutions to a Quadratic Equation

Use o discriminante para encontrar a natureza das soluções para as seguintes equações quadráticas:

1. $x^2+4x+4=0$
2. $8x^2+14x+3=0$
3. $3x^2−5x−2=0$
4. $3x^2−10x+15=0$

Solução

Calcule o discriminante$b^2−4ac$ para cada equação e indique o tipo de solução esperado.

uma.

$x^2+4x+4=0$

$b^2-4ac={(4)}^2-4(1)(4)=0$Haverá uma solução dupla racional.

b.

$8x^2+14x+3=0$

$b^2-4ac={(14)}^2-4(8)(3)=100$Como$100$ é um quadrado perfeito, haverá duas soluções racionais.

c.

$3x^2−5x−2=0$

$b^2-4ac={(-5)}^2-4(3)(-2)=49$Como$49$ é um quadrado perfeito, haverá duas soluções racionais.

d.

$3x^2−10x+15=0$

$b^2-4ac={(-10)}^2-4(3)(15)=-80$Haverá duas soluções complexas.

Usando o teorema de Pitágoras

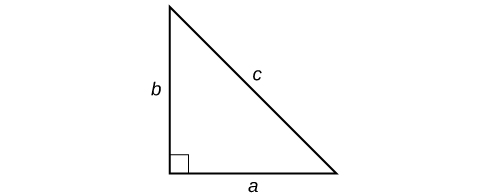
Uma das fórmulas mais famosas da matemática é o Teorema de Pitágoras. É baseado em um triângulo reto e afirma a relação entre os comprimentos dos lados como$a^2+b^2=c^2$, onde$a$ e$b$ se refere às pernas de um triângulo reto adjacente ao$90°$ ângulo, e$c$ se refere à hipotenusa. Tem usos imensuráveis em arquitetura, engenharia, ciências, geometria, trigonometria e álgebra, e em aplicações diárias.

Usamos o Teorema de Pitágoras para resolver o comprimento de um lado de um triângulo quando temos os comprimentos dos outros dois. Como cada um dos termos é quadrado no teorema, quando estamos resolvendo um lado de um triângulo, temos uma equação quadrática. Podemos usar os métodos para resolver equações quadráticas que aprendemos nesta seção para resolver o lado ausente.

O teorema de Pitágoras é dado como

$$a^2+b^2=c^2$$

onde$a$ e$b$ se refere às pernas de um triângulo reto adjacente ao$90°$ ângulo, e$c$ se refere à hipotenusa, conforme mostrado em.

Figura$\PageIndex{4}$

Exemplo$\PageIndex{12}$: Finding the Length of the Missing Side of a Right Triangle

Encontre o comprimento do lado ausente do triângulo direito na Figura$\PageIndex{5}$.

Figura$\PageIndex{5}$

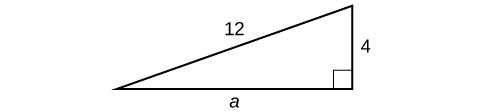
Solução

Como temos as medidas do lado$b$ e da hipotenusa, o lado que falta é$a$.

$$\begin{align*} a^2+b^2&= c^2\\ a^2+{(4)}^2&= {(12)}^2\\ a^2+16&= 144\\ a^2&= 128\\ a&= \sqrt{128}\\ &= 8\sqrt{2} \end{align*}$$

Exercício$\PageIndex{9}$

Use o Teorema de Pitágoras para resolver o problema do triângulo reto: a perna a mede 4 unidades, a perna b mede 3 unidades. Encontre o comprimento da hipotenusa.

Resposta

$5$unidades

Mídia

Acesse esses recursos on-line para obter instruções e práticas adicionais com equações quadráticas.

1. Resolvendo equações quadráticas por fatoração
2. A propriedade de produto zero
3. Completando a Praça
4. Fórmula quadrática com duas soluções racionais
5. Comprimento de uma perna de um triângulo reto

Equações-chave

fórmula quadrática

$x=\dfrac{−b±\sqrt{b^2-4ac}}{2a}$

Conceitos-chave

• Muitas equações quadráticas podem ser resolvidas fatorando quando a equação tem um coeficiente inicial de$1$ ou se a equação é uma diferença de quadrados. A propriedade do fator zero é então usada para encontrar soluções. Veja exemplo, exemplo e exemplo.
• Muitas equações quadráticas com um coeficiente principal diferente de$1$ podem ser resolvidas por fatoração usando o método de agrupamento. Veja o exemplo e o exemplo.
• Outro método para resolver o quadrático é a propriedade da raiz quadrada. A variável é quadrada. Isolamos o termo quadrado e pegamos a raiz quadrada de ambos os lados da equação. A solução produzirá uma solução positiva e negativa. Veja o exemplo e o exemplo.
• Completar o quadrado é um método de resolver equações quadráticas quando a equação não pode ser fatorada. Veja o exemplo.
• Um método altamente confiável para resolver equações quadráticas é a fórmula quadrática, com base nos coeficientes e no termo constante na equação. Veja o exemplo.
• O discriminante é usado para indicar a natureza das raízes que a equação quadrática produzirá: reais ou complexas, racionais ou irracionais e quantas de cada uma. Veja o exemplo.
• O Teorema de Pitágoras, entre os teoremas mais famosos da história, é usado para resolver problemas do triângulo reto e tem aplicações em vários campos. Resolver o comprimento de um lado de um triângulo reto requer a resolução de uma equação quadrática. Veja o exemplo.