Skip to main content
Global

3.3: Eventos independentes e mutuamente exclusivos

  1. Last updated
  2. Save as PDF
  • Page ID
    190051

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Independente e mutuamente exclusivo não significam a mesma coisa.

    Eventos independentes

    Dois eventos são independentes se o seguinte for verdadeiro:

    • \(P(\text{A|B}) = P(\text{A})\)
    • \(P(\text{B|A}) = P(\text{B})\)
    • \(P(\text{A AND B}) = P(\text{A})P(\text{B})\)

    Dois eventos\(\text{A}\) e\(\text{B}\) são independentes se o conhecimento de que um ocorreu não afeta a chance do outro ocorrer. Por exemplo, os resultados de duas funções de um dado justo são eventos independentes. O resultado da primeira jogada não altera a probabilidade do resultado da segunda jogada. Para mostrar que dois eventos são independentes, você deve mostrar apenas uma das condições acima. Se dois eventos NÃO são independentes, então dizemos que eles são dependentes.

    Amostragem de uma população

    A amostragem pode ser feita com substituição ou sem substituição (Figura\(\PageIndex{1}\)):

    • Com substituição: Se cada membro de uma população for substituído depois de ser escolhido, esse membro terá a possibilidade de ser escolhido mais de uma vez. Quando a amostragem é feita com substituição, os eventos são considerados independentes, o que significa que o resultado da primeira escolha não mudará as probabilidades da segunda escolha.
    • Sem reposição: Quando a amostragem é feita sem reposição, cada membro de uma população pode ser escolhido apenas uma vez. Nesse caso, as probabilidades da segunda escolha são afetadas pelo resultado da primeira escolha. Os eventos são considerados dependentes ou não independentes.
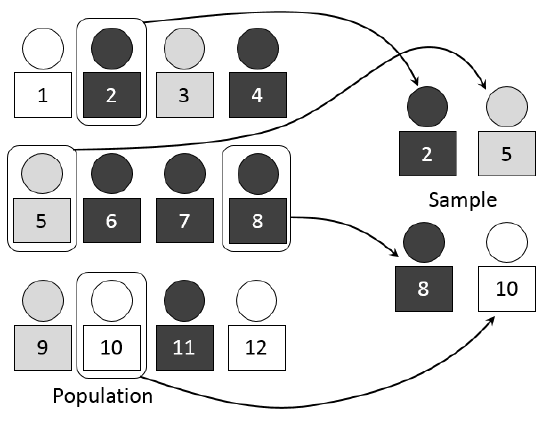
    Figura\(\PageIndex{1}\): Uma representação visual do processo de amostragem. Se os itens da amostra forem substituídos após cada evento de amostragem, então isso é “amostragem com substituição”, se não, então é “amostragem sem substituição”. Imagem usada com permissão (CC BY-SA 4.0; Dan Kernler).

    Se não se sabe se\(\text{A}\)\(\text{B}\) são independentes ou dependentes, suponha que eles sejam dependentes até que você possa mostrar o contrário.

    Exemplo\(\PageIndex{1}\): Sampling with and without replacement

    Você tem um baralho justo e bem embaralhado de 52 cartas. É composto por quatro ternos. Os trajes são paus, diamantes, corações e espadas. Há 13 cartas em cada naipe consistindo de 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,\(\text{J}\) (valete),\(\text{Q}\) (rainha),\(\text{K}\) (rei) desse naipe.

    a. Amostragem com substituição:

    Suponha que você escolha três cartas substituídas. A primeira carta que você escolhe entre as 52 cartas é a\(\text{Q}\) de espadas. Você coloca esta carta de volta, reorganiza as cartas e escolhe uma segunda carta do baralho de 52 cartas. É o dez dos clubes. Você coloca esta carta de volta, reorganiza as cartas e escolhe uma terceira carta do baralho de 52 cartas. Desta vez, a carta é a\(\text{Q}\) de espadas novamente. Suas escolhas são {\(\text{Q}\)de espadas, dez de paus,\(\text{Q}\) de espadas}. Você escolheu as\(\text{Q}\) espadas duas vezes. Você escolhe cada carta do baralho de 52 cartas.

    b. Amostragem sem substituição:

    Suponha que você escolha três cartas sem substituição. A primeira carta que você escolhe entre as 52 cartas é a\(\text{K}\) de copas. Você coloca essa carta de lado e escolhe a segunda carta das 51 cartas restantes no baralho. É o três dos diamantes. Você coloca esta carta de lado e escolhe a terceira carta das 50 cartas restantes no baralho. A terceira carta é a\(\text{J}\) de espadas. Suas escolhas são {\(\text{K}\)de corações, três de diamantes,\(\text{J}\) de espadas}. Como você escolheu as cartas sem substituí-las, você não pode escolher a mesma carta duas vezes.

    Exercício\(\PageIndex{1}\)

    Você tem um baralho justo e bem embaralhado de 52 cartas. É composto por quatro ternos. Os trajes são paus, diamantes, corações e espadas. Há 13 cartas em cada naipe consistindo de 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,\(\text{J}\) (valete),\(\text{Q}\) (rainha),\(\text{K}\) (rei) desse naipe. Três cartas são escolhidas aleatoriamente.

    1. Suponha que você saiba que as cartas escolhidas são\(\text{Q}\) de espadas,\(\text{K}\) de copas e\(\text{Q}\) de espadas. Você pode decidir se a amostragem foi com ou sem substituição?
    2. Suponha que você saiba que as cartas escolhidas são\(\text{Q}\) de espadas,\(\text{K}\) de copas e\(\text{J}\) de espadas. Você pode decidir se a amostragem foi com ou sem substituição?
    Responda a

    Com substituição

    Resposta b

    Não

    Exemplo\(\PageIndex{2}\)

    Você tem um baralho justo e bem embaralhado de 52 cartas. É composto por quatro ternos. Os trajes são paus, diamantes, corações e espadas. Há 13 cartas em cada naipe consistindo de 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,\(\text{J}\) (valete),\(\text{Q}\) (rainha) e\(\text{K}\) (rei) desse naipe. \(\text{S} =\)espadas,\(\text{H} =\) corações,\(\text{D} =\) diamantes,\(\text{C} =\) paus.

    1. Suponha que você escolha quatro cartas, mas não coloque nenhuma carta de volta no baralho. Suas cartas são\(\text{QS}, 1\text{D}, 1\text{C}, \text{QD}\).
    2. Suponha que você escolha quatro cartas e coloque cada carta de volta antes de escolher a próxima carta. Suas cartas são\(\text{KH}, 7\text{D}, 6\text{D}, \text{KH}\).

    Qual de a. ou b. você amostrou com substituição e qual você amostrou sem substituição?

    Responda a

    Sem substituição

    Resposta b

    Com substituição

    Exercício\(\PageIndex{2}\)

    Você tem um baralho justo e bem embaralhado de 52 cartas. É composto por quatro ternos. Os trajes são paus, diamantes, corações e espadas. Há 13 cartas em cada naipe consistindo de 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,\(\text{J}\) (valete),\(\text{Q}\) (rainha) e\(\text{K}\) (rei) desse naipe. \(\text{S} =\)espadas,\(\text{H} =\) corações,\(\text{D} =\) diamantes,\(\text{C} =\) paus. Suponha que você experimente quatro cartões sem substituí-los. Quais dos seguintes resultados são possíveis? Responda à mesma pergunta para amostragem com substituição.

    1. \(\text{QS}, 1\text{D}, 1\text{C}, \text{QD}\)
    2. \(\text{KH}, 7\text{D}, 6\text{D}, \text{KH}\)
    3. \(\text{QS}, 7\text{D}, 6\text{D}, \text{KS}\)
    Resposta - sem substituição

    a. Possível; b. Impossível, c. Possível

    Resposta - com substituição

    a. Possível; c. Possível, c. Possível

    Eventos mutuamente exclusivos

    \(\text{A}\)e\(\text{B}\) são eventos mutuamente exclusivos se não puderem ocorrer ao mesmo tempo. Isso significa isso\(\text{A}\) e\(\text{B}\) não compartilha nenhum resultado\(P(\text{A AND B}) = 0\) e.

    Por exemplo, suponha o espaço amostral

    \[S = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. \nonumber\]

    Deixe\(\text{A} = \{1, 2, 3, 4, 5\}, \text{B} = \{4, 5, 6, 7, 8\}\),\(\text{C} = \{7, 9\}\) e. \(\text{A AND B} = \{4, 5\}\).

    \[P(\text{A AND B}) = \dfrac{2}{10} \nonumber\]

    e não é igual a zero. Portanto,\(\text{A}\) e não\(\text{B}\) são mutuamente exclusivos. \(\text{A}\)e\(\text{C}\) não têm nenhum número em comum, então\(P(\text{A AND C}) = 0\). Portanto,\(\text{A}\) e\(\text{C}\) são mutuamente exclusivos.

    Se não se sabe se\(\text{A}\) e\(\text{B}\) são mutuamente exclusivos, suponha que não sejam até que você possa mostrar o contrário. Os exemplos a seguir ilustram essas definições e termos.

    Exemplo\(\PageIndex{3}\)

    Jogue duas moedas justas.

    O espaço da amostra é\(\{HH, HT, TH, TT\}\) onde\(T =\) as caudas e\(H =\) as cabeças. Os resultados são\(HH,HT, TH\),\(TT\) e. Os resultados\(TH\) são\(HT\) e são diferentes. \(HT\)Isso significa que a primeira moeda mostrou cabeças e a segunda moeda mostrou caudas. \(TH\)Isso significa que a primeira moeda mostrou caudas e a segunda moeda mostrou cabeças.

    • Deixe\(\text{A} =\) o evento de pegar no máximo uma cauda. (No máximo, uma cauda significa zero ou uma cauda.) Em seguida,\(\text{A}\) pode ser escrito como\(\{HH, HT, TH\}\). O resultado\(HH\) mostra zero caudas. \(HT\)e\(TH\) cada um mostra uma cauda.
    • Deixe\(\text{B} =\) o evento de obter todas as caudas. \(\text{B}\)pode ser escrito como\(\{TT\}\). \(\text{B}\)é o complemento de\(\text{A}\), então\(\text{B} = \text{A′}\). Além disso,\(P(\text{A}) + P(\text{B}) = P(\text{A}) + P(\text{A′}) = 1\).
    • As probabilidades para\(\text{A}\) e para\(\text{B}\) são\(P(\text{A}) = \dfrac{3}{4}\)\(P(\text{B}) = \dfrac{1}{4}\) e.
    • Deixe\(\text{C} =\) o evento de ganhar todas as cabeças. \(\text{C} = \{HH\}\). Desde\(\text{B} = \{TT\}\),\(P(\text{B AND C}) = 0\). \(\text{B}\)e cuidado mutuamente exclusivo. \(\text{B}\)e não\(\text{C}\) tem membros em comum porque você não pode ter todas as caudas e todas as cabeças ao mesmo tempo.)
    • Deixe o\(\text{D} =\) evento de obter mais de uma cauda. \(\text{D} = \{TT\}\). \(P(\text{D}) = \dfrac{1}{4}\)
    • Deixe o\(\text{E} =\) evento de ficar de cabeça no primeiro rolo. (Isso significa que você pode obter uma cabeça ou uma cauda no segundo rolo.) \(\text{E} = \{HT, HH\}\). \(P(\text{E}) = \dfrac{2}{4}\)
    • Encontre a probabilidade de obter pelo menos uma (uma ou duas) caudas em duas voltas. Deixe o\(\text{F} =\) evento de obter pelo menos uma cauda em duas voltas. \(\text{F} = \{HT, TH, TT\}\). \(P(\text{F}) = \dfrac{3}{4}\)

    Exercício\(\PageIndex{3}\)

    Compre duas cartas de um baralho padrão de 52 cartas com a substituição. Encontre a probabilidade de obter pelo menos uma carta preta.

    Responda

    O espaço de amostra para sacar duas cartas substituídas por um baralho padrão de 52 cartas em relação à cor é\(\{BB, BR, RB, RR\}\).

    Evento\(A =\) Obter pelo menos um cartão preto\(= \{BB, BR, RB\}\)

    \(P(\text{A}) = \dfrac{3}{4} = 0.75\)

    Exemplo\(\PageIndex{4}\)

    Jogue duas moedas justas. Encontre as probabilidades dos eventos.

    1. Deixe\(\text{F} =\) o evento de obter no máximo uma cauda (zero ou uma cauda).
    2. Deixe\(\text{G} =\) o evento de obter duas faces iguais.
    3. Deixe\(\text{H} =\) o evento de ficar com a cabeça no primeiro giro seguido por uma cabeça ou cauda no segundo giro.
    4. São\(\text{F}\) e são\(\text{G}\) mutuamente exclusivos?
    5. Deixe\(\text{J} =\) o evento de obter todas as caudas. São\(\text{J}\) e são\(\text{H}\) mutuamente exclusivos?

    Solução

    Veja o espaço da amostra em Example\(\PageIndex{3}\).

    1. Zero (0) ou um (1) caudas ocorrem quando os resultados\(HH, TH, HT\) aparecem. \(P(\text{F}) = \dfrac{3}{4}\)
    2. Duas faces são iguais se aparecerem\(HH\) ou\(TT\) aparecerem. \(P(\text{G}) = \dfrac{2}{4}\)
    3. Uma cabeça no primeiro giro seguida por uma cabeça ou cauda no segundo giro ocorre quando\(HH\) ou\(HT\) aparece. \(P(\text{H}) = \dfrac{2}{4}\)
    4. \(\text{F}\)e\(\text{G}\) compartilhar\(HH\) então não\(P(\text{F AND G})\) é igual a zero (0). \(\text{F}\)e não\(\text{G}\) são mutuamente exclusivos.
    5. Obter todas as caudas ocorre quando as caudas aparecem nas duas moedas (\(TT\)). \(\text{H}\)Os resultados da são\(HH\)\(HT\) e.

    \(\text{J}\)e não\(\text{H}\) têm nada em comum, então\(P(\text{J AND H}) = 0\). \(\text{J}\)e\(\text{H}\) são mutuamente exclusivos.

    Exercício\(\PageIndex{4}\)

    Uma caixa tem duas bolas, uma branca e outra vermelha. Selecionamos uma bola, a colocamos de volta na caixa e selecionamos uma segunda bola (amostragem com substituição). Encontre a probabilidade dos seguintes eventos:

    1. Deixe\(\text{F} =\) o evento de pegar a bola branca duas vezes.
    2. Deixe\(\text{G} =\) o evento de obter duas bolas de cores diferentes.
    3. Deixe\(\text{H} =\) o evento de ficar branco na primeira escolha.
    4. São\(\text{F}\) e são\(\text{G}\) mutuamente exclusivos?
    5. São\(\text{G}\) e são\(\text{H}\) mutuamente exclusivos?

    Responda

    1. \(P(\text{F}) = \dfrac{1}{4}\)
    2. \(P(\text{G}) = \dfrac{1}{2}\)
    3. \(P(\text{H}) = \dfrac{1}{2}\)
    4. sim
    5. Não

    Exemplo\(\PageIndex{5}\)

    Enrole um dado justo de seis lados. O espaço amostral é {1, 2, 3, 4, 5, 6}. Deixe que\(\text{A} =\) um rosto seja estranho. Então\(\text{A} = \{1, 3, 5\}\). Deixe que\(\text{B} =\) um rosto seja uniforme. Então\(\text{B} = \{2, 4, 6\}\).

    • Encontre o complemento de\(\text{A}\),\(\text{A′}\). O complemento de\(\text{A}\),\(\text{A′}\), é\(\text{B}\) porque\(\text{A}\) e\(\text{B}\) juntos compõem o espaço amostral. \(P(\text{A}) + P(\text{B}) = P(\text{A}) + P(\text{A′}) = 1\). Além disso,\(P(\text{A}) = \dfrac{3}{6}\)\(P(\text{B}) = \dfrac{3}{6}\) e.
    • Permita que o evento\(\text{C} =\) tenha faces ímpares maiores que dois. Então\(\text{C} = \{3, 5\}\). Deixe que o evento tenha\(\text{D} =\) todas as faces iguais menores que cinco. Então\(\text{D} = \{2, 4\}\). \(P(\text{C AND D}) = 0\)porque você não pode ter um rosto estranho e uniforme ao mesmo tempo. Portanto,\(\text{C}\) e\(\text{D}\) são eventos mutuamente exclusivos.
    • Deixe que\(\text{E} =\) todos os eventos enfrentem menos de cinco. \(\text{E} = \{1, 2, 3, 4\}\).

    São\(\text{C}\) eventos\(\text{E}\) mutuamente exclusivos? (Responda sim ou não.) Por que ou por que não?

    Responda

    Não. \(\text{C} = \{3, 5\}\)\(\text{E} = \{1, 2, 3, 4\}\)e. \(P(\text{C AND E}) = \dfrac{1}{6}\). Para ser mutuamente exclusivo,\(P(\text{C AND E})\) deve ser zero.

    • Encontre\(P(\text{C|A})\). Essa é uma probabilidade condicional. Lembre-se de que o evento\(\text{C}\) é {3, 5} e o evento\(\text{A}\) é {1, 3, 5}. Para encontrar\(P(\text{C|A})\), encontre a probabilidade de\(\text{C}\) usar o espaço amostral\(\text{A}\). Você reduziu o espaço amostral do espaço amostral original {1, 2, 3, 4, 5, 6} para {1, 3, 5}. Então,\(P(\text{C|A}) = \dfrac{2}{3}\).

    Exercício\(\PageIndex{5}\)

    Deixe o evento\(\text{A} =\) aprender espanhol. Let event\(\text{B}\) = aprendendo alemão. Então\(\text{A AND B}\) = aprender espanhol e alemão. Suponha\(P(\text{A}) = 0.4\)\(P(\text{B}) = 0.2\) e. \(P(\text{A AND B}) = 0.08\). Os eventos\(\text{A}\) são\(\text{B}\) independentes? Dica: Você deve mostrar UMA das seguintes opções:

    • \(P(\text{A|B}) = P(\text{A})\)
    • \(P(\text{B|A})\)
    • \(P(\text{A AND B}) = P(\text{A})P(\text{B})\)

    Responda

    \[P(\text{A|B}) = \dfrac{\text{P(A AND B)}}{P(\text{B})} = \dfrac{0.08}{0.2} = 0.4 = P(\text{A})\]

    Os eventos são independentes porque\(P(\text{A|B}) = P(\text{A})\).

    Exemplo\(\PageIndex{6}\)

    Deixe o evento\(\text{G} =\) fazer uma aula de matemática. Deixe o evento\(\text{H} =\) fazer uma aula de ciências. Em seguida,\(\text{G AND H} =\) fazendo uma aula de matemática e uma aula de ciências. Suponha\(P(\text{G}) = 0.6\) que\(P(\text{H}) = 0.5\),\(P(\text{G AND H}) = 0.3\) e. São\(\text{G}\)\(\text{H}\) independentes?

    Se\(\text{G}\) e\(\text{H}\) forem independentes, você deverá mostrar UMA das seguintes opções:

    • \(P(\text{G|H}) = P(\text{G})\)
    • \(P(\text{H|G}) = P(\text{H})\)
    • \(P(\text{G AND H}) = P(\text{G})P(\text{H})\)

    A escolha que você faz depende das informações que você tem. Você pode escolher qualquer um dos métodos aqui porque tem as informações necessárias.

    1. a. Mostre isso\(P(\text{G|H}) = P(\text{G})\).
    2. b. Mostre\(P(\text{G AND H}) = P(\text{G})P(\text{H})\).

    Solução

    1. \(P(\text{G|H}) = \dfrac{P(\text{G AND H})}{P(\text{H})} = \dfrac{0.3}{0.5} = 0.6 = P(\text{G})\)
    2. \(P(\text{G})P(\text{H}) = (0.6)(0.5) = 0.3 = P(\text{G AND H})\)

    Como\(\text{G}\) e\(\text{H}\) são independentes, saber que uma pessoa está fazendo uma aula de ciências não muda a chance de ela estar fazendo uma aula de matemática. Se os dois eventos não tivessem sido independentes (ou seja, são dependentes), saber que uma pessoa está fazendo uma aula de ciências mudaria a chance de ela estar fazendo matemática. Para praticar, mostre isso\(P(\text{H|G}) = P(\text{H})\) para mostrar isso\(\text{G}\) e\(\text{H}\) são eventos independentes.

    Exercício\(\PageIndex{6}\)

    Em uma bolsa, há seis bolinhas vermelhas e quatro bolinhas verdes. As bolas vermelhas são marcadas com os números 1, 2, 3, 4, 5 e 6. As bolas verdes são marcadas com os números 1, 2, 3 e 4.

    • \(\text{R} =\)um mármore vermelho
    • \(\text{G} =\)um mármore verde
    • \(\text{O} =\)uma bola de gude com números ímpares
    • O espaço da amostra é\(\text{S} = \{R1, R2, R3, R4, R5, R6, G1, G2, G3, G4\}\).

    \(\text{S}\)tem dez resultados. O que é\(P(\text{G AND O})\)?

    Responda

    Evento\(\text{G}\) e\(\text{O} = \{G1, G3\}\)

    \(P(\text{G and O}) = \dfrac{2}{10} = 0.2\)

    Exemplo\(\PageIndex{7}\)

    Deixe o evento\(\text{C} =\) fazer uma aula de inglês. Deixe o evento\(\text{D} =\) fazer uma aula de discurso.

    Suponha\(P(\text{C}) = 0.75\) que\(P(\text{D}) = 0.3\),\(P(\text{C|D}) = 0.75\)\(P(\text{C AND D}) = 0.225\) e.

    Justifique suas respostas às seguintes perguntas numericamente.

    1. São\(\text{C}\)\(\text{D}\) independentes?
    2. São\(\text{C}\) e são\(\text{D}\) mutuamente exclusivos?
    3. O que é\(P(\text{D|C})\)?

    Solução

    1. Sim, porque\(P(\text{C|D}) = P(\text{C})\).
    2. Não, porque não\(P(\text{C AND D})\) é igual a zero.
    3. \(P(\text{D|C}) = \dfrac{P(\text{C AND D})}{P(\text{C})} = \dfrac{0.225}{0.75} = 0.3\)

    Exercício\(\PageIndex{7}\)

    Um estudante vai à biblioteca. Deixe\(\text{B} =\) os eventos em que o aluno confere um livro e\(\text{D} =\) o aluno confere um DVD. Suponha que\(P(\text{B}) = 0.40\),\(P(\text{D}) = 0.30\)\(P(\text{B AND D}) = 0.20\) e.

    1. Encontre\(P(\text{B|D})\).
    2. Encontre\(P(\text{D|B})\).
    3. São\(\text{B}\)\(\text{D}\) independentes?
    4. São\(\text{B}\) e são\(\text{D}\) mutuamente exclusivos?

    Responda

    1. \(P(\text{B|D}) = 0.6667\)
    2. \(P(\text{D|B}) = 0.5\)
    3. Não
    4. Não

    Exemplo\(\PageIndex{8}\)

    Em uma caixa há três cartões vermelhos e cinco cartões azuis. Os cartões vermelhos são marcados com os números 1, 2 e 3, e os cartões azuis são marcados com os números 1, 2, 3, 4 e 5. As cartas estão bem embaralhadas. Você entra na caixa (não consegue vê-la) e tira uma carta.

    Deixe

    • \(\text{R =}\)cartão vermelho é sorteado,
    • \(\text{B} =\)o cartão azul é sorteado,
    • \(\text{E} =\)o cartão de número par é sorteado.

    O espaço da amostra\(S = R1, R2, R3, B1, B2, B3, B4, B5\).

    \(S\)tem oito resultados.

    • \(P(\text{R}) = \dfrac{3}{8}\). \(P(\text{B}) = \dfrac{5}{8}\). \(P(\text{R AND B}) = 0\). (Você não pode comprar uma carta que seja vermelha e azul.)
    • \(P(\text{E}) = \dfrac{3}{8}\). (Existem três cartas de números pares\(R2, B2\),\(B4\) e.)
    • \(P(\text{E|B}) = \dfrac{2}{5}\). (Existem cinco cartões azuis:\(B1, B2, B3, B4\),\(B5\) e. Dos cartões azuis, há dois cartões pares;\(B2\)\(B4\) e.)
    • \(P(\text{B|E}) = \dfrac{2}{3}\). (Existem três cartas de números pares:\(R2, B2\),\(B4\) e. Dos cartões pares, dois são azuis;\(B2\)\(B4\) e.)
    • Os eventos\(\text{R}\)\(\text{B}\) são mutuamente exclusivos porque\(P(\text{R AND B}) = 0\).
    • Deixe um\(\text{G} =\) cartão com um número maior que 3. \(\text{G} = \{B4, B5\}\). \(P(\text{G}) = \dfrac{2}{8}\). Deixe o cartão\(\text{H} =\) azul numerado entre um e quatro, inclusive. \(\text{H} = \{B1, B2, B3, B4\}\). \(P(\text{G|H}) = \frac{1}{4}\). (A única carta\(\text{H}\) que tem um número maior que três é B4.) Desde\(\dfrac{2}{8} = \dfrac{1}{4}\),\(P(\text{G}) = P(\text{G|H})\), o que significa isso\(\text{G}\) e\(\text{H}\) são independentes.

    Exercício\(\PageIndex{8}\)

    Em uma arena de basquete,

    • 70% dos torcedores estão torcendo pelo time da casa.
    • 25% dos fãs estão vestindo azul.
    • 20% dos torcedores estão vestindo azul e torcendo pelo time visitante.
    • Dos torcedores que torcem pela equipe visitante, 67% estão vestindo azul.

    \(\text{A}\)Seja o caso de um torcedor torcer pelo time visitante.

    \(\text{B}\)Seja o caso de um fã estar vestindo azul.

    Os eventos de torcer pela equipe visitante e vestir o azul são independentes? Eles são mutuamente exclusivos?

    Responda

    • \(P(\text{B|A}) = 0.67\)
    • \(P(\text{B}) = 0.25\)

    Então\(P(\text{B})\) não é igual\(P(\text{B|A})\), o que significa que não\(\text{B} and \text{A}\) são independentes (vestir azul e torcer pela equipe visitante não são independentes). Eles também não são mutuamente exclusivos\(P(\text{B AND A}) = 0.20\), porque não\(0\).

    Exemplo\(\PageIndex{9}\)

    Em uma determinada turma universitária, 60% dos estudantes são do sexo feminino. Cinquenta por cento de todos os alunos da turma têm cabelos compridos. Quarenta e cinco por cento dos estudantes são do sexo feminino e têm cabelos compridos. Das alunas, 75% têm cabelos compridos. \(\text{F}\)Seja o caso de uma estudante ser mulher. \(\text{L}\)Seja o caso de um aluno ter cabelos compridos. Um aluno é escolhido aleatoriamente. Os eventos de ser mulher e ter cabelos compridos são independentes?

    • As seguintes probabilidades são dadas neste exemplo:
    • \(P(\text{F}) = 0.60\);\(P(\text{L}) = 0.50\)
    • \(P(\text{F AND L}) = 0.45\)
    • \(P(\text{L|F}) = 0.75\)

    A escolha que você faz depende das informações que você tem. Você pode usar a primeira ou a última condição na lista para este exemplo. Você\(P(\text{F|L})\) ainda não sabe, então não pode usar a segunda condição.

    Solução 1

    Verifique se\(P(\text{F AND L}) = P(\text{F})P(\text{L})\). Nós recebemos isso\(P(\text{F AND L}) = 0.45\), mas\(P(\text{F})P(\text{L}) = (0.60)(0.50) = 0.30\). Os eventos de ser mulher e ter cabelos compridos não são independentes porque\(P(\text{F AND L})\) não são iguais\(P(\text{F})P(\text{L})\).

    Solução 2

    Verifique se\(P(\text{L|F})\) é igual\(P(\text{L})\). Nós recebemos isso\(P(\text{L|F}) = 0.75\), mas\(P(\text{L}) = 0.50\); eles não são iguais. Os eventos de ser mulher e ter cabelos compridos não são independentes.

    Interpretação dos resultados

    Os eventos de ser mulher e ter cabelos compridos não são independentes; saber que um aluno é mulher muda a probabilidade de o aluno ter cabelo comprido.

    Exercício\(\PageIndex{9}\)

    Mark está decidindo qual caminho seguir para o trabalho. Suas escolhas são\(\text{I} = \text{the Interstate}\) e\(\text{F} = \text{Fifth Street}\)

    • \(P(\text{I}) = 0.44\)e\(P(\text{F}) = 0.55\)
    • \(P(\text{I AND F}) = 0\)porque Mark seguirá apenas uma rota para o trabalho.

    Qual é a probabilidade de\(P(\text{I OR F})\)?

    Responda

    Porque\(P(\text{I AND F}) = 0\),

    \(P(\text{I OR F}) = P(\text{I}) + P(\text{F}) - P(\text{I AND F}) = 0.44 + 0.56 - 0 = 1\)

    Exemplo\(\PageIndex{10}\)

    1. Jogue uma moeda justa (a moeda tem dois lados\(\text{H}\) e\(\text{T}\)). Os resultados são ________. Conte os resultados. Existem ____ resultados.
    2. Lance um dado justo de seis lados (o dado tem 1, 2, 3, 4, 5 ou 6 pontos em um lado). Os resultados são ________________. Conte os resultados. Existem ___ resultados.
    3. Multiplique os dois números de resultados. A resposta é _______.
    4. Se você jogar uma moeda justa e segui-la com o lançamento de um dado justo de seis lados, a resposta em três é o número de resultados (tamanho do espaço amostral). Quais são os resultados? (Dica: dois dos resultados são\(H1\)\(T6\) e.)
    5. \(\text{A} =\)Cabeças de evento (\(\text{H}\)) na moeda seguidas por um número par (2, 4, 6) no dado.
      \(\text{A}\)= {_________________}. Encontre\(P(\text{A})\).
    6. O evento\(\text{B} =\) encabeça na moeda, seguido por um três no dado. \(\text{B} =\){________}. Encontre\(P(\text{B})\).
    7. São\(\text{A}\) e são\(\text{B}\) mutuamente exclusivos? (Dica: O que é\(P(\text{A AND B})\)? Se\(P(\text{A AND B}) = 0\), então\(\text{A}\) e\(\text{B}\) são mutuamente exclusivos.)
    8. São\(\text{A}\)\(\text{B}\) independentes? (Dica: É\(P(\text{A AND B}) = P(\text{A})P(\text{B})\)? Se\(P(\text{A AND B})\ = P(\text{A})P(\text{B})\), então\(\text{A}\) e\(\text{B}\) são independentes. Caso contrário, eles são dependentes).

    Solução

    1. \(\text{H}\)e 2\(\text{T}\);
    2. 1, 2, 3, 4, 5, 6;
    3. 2 (6) = 12
    4. \(T1, T2, T3, T4, T5, T6, H1, H2, H3, H4, H5, H6\)
    5. \(\text{A} = \{H2, H4, H6\}\);\(P(\text{A}) = \dfrac{3}{12}\)
    6. \(\text{B} = \{H3\}\);\(P(\text{B}) = \dfrac{1}{12}\)
    7. Sim, porque\(P(\text{A AND B}) = 0\)
    8. \(P(\text{A AND B}) = 0\). \(P(\text{A})P(\text{B}) = \left(\dfrac{3}{12}\right)\left(\dfrac{1}{12}\right)\). \(P(\text{A AND B})\)não é igual\(P(\text{A})P(\text{B})\), então\(\text{A}\) e\(\text{B}\) são dependentes.

    Exercício\(\PageIndex{10}\)

    Uma caixa tem duas bolas, uma branca e outra vermelha. Selecionamos uma bola, a colocamos de volta na caixa e selecionamos uma segunda bola (amostragem com substituição). \(\text{T}\)Seja o evento de pegar a bola branca duas vezes,\(\text{F}\) o evento de escolher a bola branca primeiro,\(\text{S}\) o evento de escolher a bola branca no segundo sorteio.

    1. Computar\(P(\text{T})\).
    2. Computar\(P(\text{T|F})\).
    3. São\(\text{T}\)\(\text{F}\) independentes?.
    4. São\(\text{F}\) e são\(\text{S}\) mutuamente exclusivos?
    5. São\(\text{F}\)\(\text{S}\) independentes?

    Responda

    1. \(P(\text{T}) = \dfrac{1}{4}\)
    2. \(P(\text{T|F}) = \dfrac{1}{2}\)
    3. Não
    4. Não
    5. sim

    Referências

    1. Lopez, Shane e Preety Sidhu. “Os professores dos EUA amam suas vidas, mas lutam no local de trabalho.” Gallup Wellbeing, 2013. http://www.gallup.com/poll/161516/te...workplace.aspx (acessado em 2 de maio de 2013).
    2. Dados da Gallup. Disponível on-line em www.gallup.com/ (acessado em 2 de maio de 2013).

    Revisão

    Dois eventos\(\text{A}\) e\(\text{B}\) são independentes se o conhecimento de que um ocorreu não afeta a chance do outro ocorrer. Se dois eventos não são independentes, então dizemos que eles são dependentes.

    Na amostragem com reposição, cada membro de uma população é substituído após a coleta, para que o membro tenha a possibilidade de ser escolhido mais de uma vez e os eventos sejam considerados independentes. Na amostragem sem reposição, cada membro de uma população pode ser escolhido apenas uma vez, e os eventos são considerados não independentes. Quando os eventos não compartilham resultados, eles são mutuamente exclusivos um do outro.

    Revisão da fórmula

    • Se\(\text{A}\) e\(\text{B}\) forem independentes,\(P(\text{A AND B}) = P(\text{A})P(\text{B}), P(\text{A|B}) = P(\text{A})\)\(P(\text{B|A}) = P(\text{B})\) e.
    • Se\(\text{A}\) e\(\text{B}\) forem mutuamente exclusivos,\(P(\text{A OR B}) = P(\text{A}) + P(\text{B}) and P(\text{A AND B}) = 0\).

    Exercício\(\PageIndex{11}\)

    \(\text{E}\)e\(\text{F}\) são eventos mutuamente exclusivos. \(P(\text{E}) = 0.4\);\(P(\text{F}) = 0.5\). Encontre\(P(\text{E∣F})\).

    Exercício\(\PageIndex{12}\)

    \(\text{J}\)e\(\text{K}\) são eventos independentes. \(P(\text{J|K}) = 0.3\). Encontre\(P(\text{J})\).

    Responda

    \(P(\text{J}) = 0.3\)

    Exercício\(\PageIndex{13}\)

    \(\text{U}\)e\(\text{V}\) são eventos mutuamente exclusivos. \(P(\text{U}) = 0.26\);\(P(\text{V}) = 0.37\). Encontre:

    1. \(P(\text{U AND V}) =\)
    2. \(P(\text{U|V}) =\)
    3. \(P(\text{U OR V}) =\)

    Exercício\(\PageIndex{14}\)

    \(\text{Q}\)e\(\text{R}\) são eventos independentes. \(P(\text{Q}) = 0.4\)\(P(\text{Q AND R}) = 0.1\)e. Encontre\(P(\text{R})\).

    Responda

    \(P(\text{Q AND R}) = P(\text{Q})P(\text{R})\)

    \(0.1 = (0.4)P(\text{R})\)

    \(P(\text{R}) = 0.25\)

    Reunindo tudo

    Exercício\(\PageIndex{16}\)

    No ano anterior, os pesos dos membros do San Francisco 49ers e do Dallas Cowboys foram publicados no San Jose Mercury News. Os dados factuais são compilados na Tabela.

    Camisa# ≤ 210 211—250 251—290 290≤
    1—33 21 5 0 0
    34—66 6 18 7 4
    66—99 6 12 22 5

    Para o seguinte, suponha que você selecione aleatoriamente um jogador dos 49ers ou Cowboys.

    Se ter um número de camisa de um a 33 e pesar no máximo 210 libras eram eventos independentes, então o que deveria ser verdade\(P(\text{Shirt} \#1–33|\leq 210 \text{ pounds})\)?

    Exercício\(\PageIndex{17}\)

    A probabilidade de um homem desenvolver algum tipo de câncer durante sua vida é de 0,4567. A probabilidade de um homem ter pelo menos um resultado de teste falso positivo (o que significa que o teste volta para câncer quando o homem não o tem) é de 0,51. Algumas das perguntas a seguir não têm informações suficientes para você respondê-las. Escreva “informações insuficientes” para essas respostas. Deixe que\(\text{C} =\) um homem desenvolva câncer durante sua vida e o\(\text{P} =\) homem tenha pelo menos um falso positivo.

    1. \(P(\text{C}) =\)______
    2. \(P(\text{P|C}) =\)______
    3. \(P(\text{P|C'}) =\)______
    4. Se um teste der positivo, com base em valores numéricos, você pode presumir que o homem tem câncer? Justifique numericamente e explique por que ou por que não.

    Responda

    1. \(P(\text{C}) = 0.4567\)
    2. informações insuficientes
    3. informações insuficientes
    4. Não, porque mais da metade (0,51) dos homens tem pelo menos um texto falso positivo

    Exercício\(\PageIndex{18}\)

    Eventos dados\(\text{G}\) e\(\text{H}: P(\text{G}) = 0.43\)\(P(\text{H}) = 0.26\);\(P(\text{H AND G}) = 0.14\)

    1. Encontre\(P(\text{H OR G})\).
    2. Encontre a probabilidade do complemento do evento (\(\text{H AND G}\)).
    3. Encontre a probabilidade do complemento do evento (\(\text{H OR G}\)).

    Exercício\(\PageIndex{19}\)

    Eventos dados\(\text{J}\) e\(\text{K}: P(\text{J}) = 0.18\)\(P(\text{K}) = 0.37\);\(P(\text{J OR K}) = 0.45\)

    1. Encontre\(P(\text{J AND K})\).
    2. Encontre a probabilidade do complemento do evento (\(\text{J AND K}\)).
    3. Encontre a probabilidade do complemento do evento (\(\text{J AND K}\)).

    Responda

    1. \(P(\text{J OR K}) = P(\text{J}) + P(\text{K}) − P(\text{J AND K}); 0.45 = 0.18 + 0.37 - P(\text{J AND K})\); resolva para encontrar\(P(\text{J AND K}) = 0.10\)
    2. \(P(\text{NOT (J AND K)}) = 1 - P(\text{J AND K}) = 1 - 0.10 = 0.90\)
    3. \(P(\text{NOT (J OR K)}) = 1 - P(\text{J OR K}) = 1 - 0.45 = 0.55\)

    Glossário

    Eventos dependentes
    Se dois eventos NÃO são independentes, então dizemos que eles são dependentes.
    Amostragem com substituição
    Se cada membro de uma população for substituído depois de ser escolhido, esse membro terá a possibilidade de ser escolhido mais de uma vez.
    Amostragem sem substituição
    Quando a amostragem é feita sem reposição, cada membro de uma população pode ser escolhido apenas uma vez.
    A probabilidade condicional de um evento dado outro evento
    P (A | B) é a probabilidade de que o evento A ocorra, dado que o evento B já ocorreu.
    O OR de dois eventos
    Um resultado está no evento A OU B se o resultado estiver em A, em B ou em A e B.