9.4: Multiplique raízes quadradas
- Page ID
- 184045
Ao final desta seção, você poderá:
- Multiplique raízes quadradas
- Use a multiplicação polinomial para multiplicar raízes quadradas
Antes de começar, faça este teste de prontidão.
- Simplifique: (3u) (8v).
Se você perdeu esse problema, consulte o Exemplo 6.2.31. - Simplifique: 6 (12−7n).
Se você perdeu esse problema, consulte o Exemplo 6.3.1. - Simplifique: (2+a) (4−a).
Se você perdeu esse problema, consulte o Exemplo 6.3.34.
Multiplique raízes quadradas
Usamos a propriedade de produto das raízes quadradas para simplificar as raízes quadradas, removendo os fatores quadrados perfeitos. A propriedade do produto da Square Roots diz
\[\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber\]
Podemos usar a propriedade de produto das raízes quadradas “ao contrário” para multiplicar as raízes quadradas.
\[\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber\]
Lembre-se de que assumimos que todas as variáveis são maiores ou iguais a zero.
Vamos reescrever a propriedade de produto da Square Roots para que possamos ver os dois lados juntos.
Se a, b são números reais não negativos, então
\(\sqrt{ab}=\sqrt{a}·\sqrt{b}\)\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\)e.
Então, podemos multiplicar\(\sqrt{3}·\sqrt{5}\) in this way:
\[\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}\]
Às vezes, o produto nos dá um quadrado perfeito:
\[\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}\]
Mesmo quando o produto não é um quadrado perfeito, devemos buscar fatores de quadrado perfeito e simplificar o radical sempre que possível.
Multiplicar radicais por coeficientes é muito parecido com multiplicar variáveis por coeficientes. Para multiplicar 4x·3y, multiplicamos os coeficientes juntos e depois as variáveis. O resultado é 12xy. Lembre-se disso ao fazer esses exemplos.
Simplifique:
- \(\sqrt{2}·\sqrt{6}\)
- \((4\sqrt{3})(2\sqrt{12})\).
- Resposta
-
1. \(\sqrt{2}·\sqrt{6}\) Multiplique usando a propriedade do produto. \(\sqrt{12}\) Simplifique o radical. \(\sqrt{4}·\sqrt{3}\) Simplifique. \(2\sqrt{3}\) 2. \((4\sqrt{3})(2\sqrt{12})\) Multiplique usando a propriedade do produto. \(8\sqrt{36}\) Simplifique o radical. \(8·6\) Simplifique. \(48\)
Simplifique:
- \(\sqrt{3}·\sqrt{6}\)
- \((2\sqrt{6})(3\sqrt{12})\).
- Resposta
-
- \(3\sqrt{2}\)
- \(36\sqrt{2}\)
Simplifique:
- \(\sqrt{5}·\sqrt{10}\)
- \((6\sqrt{3})(5\sqrt{6})\)
- Resposta
-
- \(5\sqrt{2}\)
- \(90\sqrt{2}\)
Simplifique:\((6\sqrt{2})(3\sqrt{10})\)
- Resposta
-
\((6\sqrt{2})(3\sqrt{10})\) Multiplique usando a propriedade do produto. \(18\sqrt{20}\) Simplifique o radical. \(18\sqrt{4}·\sqrt{5}\) Simplifique. \(18·2·\sqrt{5}\) \(36\sqrt{5}\)
Simplifique:\((3\sqrt{2})(2\sqrt{30})\)
- Resposta
-
\(12\sqrt{15}\)
Simplifique:\((3\sqrt{3})(3\sqrt{6})\).
- Resposta
-
\(27\sqrt{2}\)
Quando temos que multiplicar raízes quadradas, primeiro encontramos o produto e depois removemos quaisquer fatores quadrados perfeitos.
Simplifique:
- \((\sqrt{8x^3})(\sqrt{3x})\)
- \((\sqrt{20y^2})(\sqrt{5y^3})\)
- Resposta
-
1. \((\sqrt{8x^3})(\sqrt{3x})\) Multiplique usando a propriedade do produto. \(\sqrt{24x^4}\) Simplifique o radical. \(\sqrt{4x^4}·\sqrt{6}\) Simplifique. \(2x^2\sqrt{6}\) 2. \((\sqrt{20y^2})(\sqrt{5y^3})\) Multiplique usando a propriedade do produto. \(\sqrt{100y^5}\) Simplifique o radical. \(10y^2\sqrt{y}\)
Simplifique:
- \((\sqrt{6x^3})(\sqrt{3x})\)
- \((\sqrt{2y^3})(\sqrt{50y^2})\).
- Resposta
-
- \(3x^2\sqrt{2}\)
- \(10y^2\sqrt{y}\)
Simplifique:
- \((\sqrt{6x^5})(\sqrt{2x})\)
- \((\sqrt{12y^2})(\sqrt{3y^5})\)
- Resposta
-
- \(2x^3\sqrt{3}\)
- \(6y^2\sqrt{y}\)
Simplifique:\((10\sqrt{6p^3})(3\sqrt{18p})\)
- Resposta
-
\((10\sqrt{6p^3})(3\sqrt{18p})\) Multiplique. \(30\sqrt{108p^4}\) Simplifique o radical. \(30\sqrt{36p^4}·\sqrt{3}\) \(30·6p^2·\sqrt{3}\) \(180p^2\sqrt{3}\)
Simplifique:\((\sqrt{62x^2})(8\sqrt{45x^4})\)
- Resposta
-
\(144x^3\sqrt{10}\)
Simplifique:\((2\sqrt{6y^4})(12\sqrt{30y})\).
- Resposta
-
\(144y^2\sqrt{5y}\)
Simplifique:
- \((\sqrt{2})^2\)
- \((−\sqrt{11})^2\).
- Resposta
-
1. \((\sqrt{2})^2\) Reescreva como um produto. \((\sqrt{2})(\sqrt{2})\) Multiplique. \(\sqrt{4}\) Simplifique. 2 2. \((−\sqrt{11})^2\) Reescreva como um produto. \((−\sqrt{11})(−\sqrt{11})\) Multiplique. \(\sqrt{121}\) Simplifique. 11
Simplifique:
- \((\sqrt{12})^2\)
- \((−\sqrt{15})^2\).
- Resposta
-
- 12
- 15
Simplifique:
- \((\sqrt{16})^2\)
- \((−\sqrt{20})^2\).
- Resposta
-
- 16
- 20
Os resultados do exemplo anterior nos conduzem a essa propriedade.
Se a for um número real não negativo, então
\((\sqrt{a})^2=a\)
Ao perceber que quadrar e obter uma raiz quadrada são operações “opostas”, podemos simplificar\((\sqrt{2})^2\) e obter 2 imediatamente. Quando multiplicamos as duas raízes quadradas na parte (a) do próximo exemplo, é o mesmo que quadrar.
Simplifique:
- \((2\sqrt{3})(8\sqrt{3})\)
- \((3\sqrt{6})^2\).
- Resposta
-
1. \((2\sqrt{3})(8\sqrt{3})\) Multiplique. Lembre-se,\((\sqrt{3}^2)\) 16·3 Simplifique. 48 2. \((3\sqrt{6})^2\) Multiplique. 9,6 Simplifique. 54
Simplifique:
- \((6\sqrt{11})(5\sqrt{11})\)
- \((5\sqrt{8})^2\).
- Resposta
-
- 330
- 200
Simplifique:
- \((3\sqrt{7})(10\sqrt{7})\)
- \((−4\sqrt{6})^2\).
- Resposta
-
- 210
- 96
Use a multiplicação polinomial para multiplicar raízes quadradas
Nos próximos exemplos, usaremos a Propriedade Distributiva para multiplicar expressões com raízes quadradas.
Primeiro distribuiremos e depois simplificaremos as raízes quadradas quando possível.
Simplifique:
- \(3(5−\sqrt{2})\)
- \(\sqrt{2}(4−\sqrt{10})\).
- Resposta
-
1. \(3(5−\sqrt{2})\) Distribuir. \(15−3\sqrt{2})\) 2. \(\sqrt{2}(4−\sqrt{10})\) Distribuir. \(4\sqrt{2}−\sqrt{20}\) Simplifique. \(4\sqrt{2}−2\sqrt{5}\)
Simplifique:
- \(2(3−\sqrt{5})\)
- \(\sqrt{3}(2−\sqrt{18})\).
- Resposta
-
- \(6−2\sqrt{5}\)
- \(2\sqrt{3}−3\sqrt{6}\)
Simplifique:
- \(6(2+\sqrt{6})\)
- \(\sqrt{7}(1+\sqrt{14})\).
- Resposta
-
- \(12+\sqrt{6}\)
- \(\sqrt{7}+7\sqrt{2}\)
Simplifique:
- \(\sqrt{5}(7+2\sqrt{5})\)
- \(\sqrt{6}(\sqrt{2}+\sqrt{18})\).
- Resposta
-
1. \(\sqrt{5}(7+2\sqrt{5})\) Distribuir. \(7\sqrt{5}+2·5\) Simplifique. \(7\sqrt{5}+10\) \(10+7\sqrt{5}\) 2. \(\sqrt{6}(\sqrt{2}+\sqrt{18})\) Multiplique. \(\sqrt{12}+\sqrt{108}\) Simplifique. \((\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})\) \(2\sqrt{3}+6\sqrt{3}\) Combine como radicais. \(8\sqrt{3}\)
Simplifique:
- \(\sqrt{6}(1+3\sqrt{6})\)
- \(\sqrt{12}(\sqrt{3}+\sqrt{24})\)
- Resposta
-
- \(18+\sqrt{6}\)
- \(6+12\sqrt{2}\)
Simplifique:
- \(\sqrt{8}(2−5\sqrt{8})\)
- \(\sqrt{14}(\sqrt{2}+\sqrt{42})\)
- Resposta
-
- \(−40+4\sqrt{2}\)
- \(2\sqrt{7}+14\sqrt{3}\)
Quando trabalhamos com polinômios, multiplicamos binômios por binômios. Lembre-se de que isso nos deu quatro produtos antes de combinarmos termos semelhantes. Para ter certeza de adquirir todos os quatro produtos, organizamos nosso trabalho, geralmente pelo método FOIL.
Simplifique:\((2+\sqrt{3})(4−\sqrt{3})\)
- Resposta
-
\((2+\sqrt{3})(4−\sqrt{3})\) Multiplique. \(8−2\sqrt{3}+4\sqrt{3}−3\) Combine termos semelhantes. \(5+2\sqrt{3}\)
Simplifique:\((1+\sqrt{6})(3−\sqrt{6})\).
- Responda
-
\(−3+2\sqrt{6}\)
Simplifique:\((4−\sqrt{10})(2+\sqrt{10})\).
- Responda
-
\(−2+2\sqrt{10}\)
Simplifique:\((3−2\sqrt{7})(4−2\sqrt{7})\).
- Responda
-
\((3−2\sqrt{7})(4−2\sqrt{7})\) Multiplique. \(12−6\sqrt{7}−8\sqrt{7}+4·7\) Simplifique. \(12−6\sqrt{7}−8\sqrt{7}+28\) Combine termos semelhantes. \(40−14\sqrt{7}\)
Simplifique:\((6−3\sqrt{7})(3+4\sqrt{7})\).
- Responda
-
\(−66+15\sqrt{7}\)
Simplifique:\((2−3\sqrt{11})(4−\sqrt{11})\)
- Responda
-
\(41+14\sqrt{11}\)
Simplifique:\((3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\).
- Responda
-
\(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\) Multiplique. \(3·2+12\sqrt{10}−\sqrt{10}−4·5\) Simplifique. \(6+12\sqrt{10}−\sqrt{10}−20\) Combine termos semelhantes. \(−14+11\sqrt{10}\)
Simplifique:\((5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})\)
- Responda
-
\(1+9\sqrt{21}\)
Simplifique:\((\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})\)
- Responda
-
\(−12−20\sqrt{3}\)
Simplifique:\((4−2\sqrt{x})(1+3\sqrt{x})\).
- Responda
-
\((4−2\sqrt{x})(1+3\sqrt{x})\). Multiplique. \(4+12\sqrt{x}−2\sqrt{x}−6x\) Combine termos semelhantes. \(4+10\sqrt{x}−6x\)
Simplifique:\((6−5\sqrt{m})(2+3\sqrt{m})\).
- Responda
-
\(12+8\sqrt{m}−15m\)
Simplifique:\((10+3\sqrt{n})(1−5\sqrt{n})\)
- Responda
-
\(10−47\sqrt{n}−15n\)
Observe que alguns produtos especiais facilitaram nosso trabalho quando multiplicamos binômios anteriormente. Isso também é verdade quando multiplicamos raízes quadradas. As fórmulas de produtos especiais que usamos são mostradas abaixo.
\[\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}\]
Usaremos as fórmulas de produtos especiais nos próximos exemplos. Começaremos com a fórmula dos Quadrados Binomiais.
Simplifique:
- \((2+\sqrt{3})^2\)
- \((4−2\sqrt{5})^2\).
- Responda
-
Certifique-se de incluir o termo 2ab ao quadrar um binômio.
1.
2.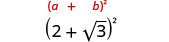
Multiplique usando o padrão binomial quadrado. 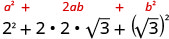
Simplifique. 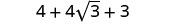
Combine termos semelhantes. 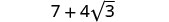
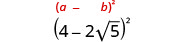
Multiplique usando o padrão binomial quadrado. 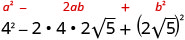
Simplifique. 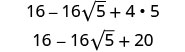
Combine termos semelhantes. 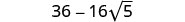
Simplifique:
- \((10+\sqrt{2})^2\)
- \((1+3\sqrt{6})^2\).
- Responda
-
- \(102+20\sqrt{2}\)
- \(55+6\sqrt{6}\)
Simplifique:
- \((6-\sqrt{5})^2\)
- \((9-2\sqrt{10})^2\).
- Responda
-
- \(41-12\sqrt{5}\)
- \(121-36\sqrt{10}\)
Simplifique:\((1+3\sqrt{x})^2\).
- Responda
-
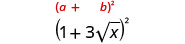
Multiplique usando o padrão binomial quadrado. 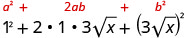
Simplifique. 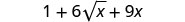
Simplifique:\((2+5\sqrt{m})^2\).
- Responda
-
\(4+20\sqrt{m}+25m\)
Simplifique:\((3−4\sqrt{n})^2\).
- Responda
-
\(9−24\sqrt{n}+16n\)
Nos próximos dois exemplos, encontraremos o produto dos conjugados.
Simplifique:\((4−\sqrt{2})(4+\sqrt{2})\).
- Responda
-
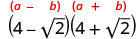
Multiplique usando o padrão binomial quadrado. 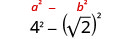
Simplifique. 
Simplifique:\((2−\sqrt{3})(2+\sqrt{3})\)
- Responda
-
1
Simplifique:\((1+\sqrt{5})(1−\sqrt{5})\)
- Responda
-
−4
Simplifique:\((5−2\sqrt{3})(5+2\sqrt{3})\)
- Responda
-
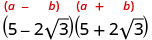
Multiplique usando o padrão binomial quadrado. 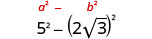
Simplifique. 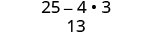
Simplifique:\((3−2\sqrt{5})(3+2\sqrt{5})\).
- Responda
-
−11
Simplifique:\((4+5\sqrt{7})(4−5\sqrt{7})\).
- Responda
-
−159
Acesse esses recursos on-line para obter instruções e práticas adicionais com a multiplicação de raízes quadradas.
- Propriedade do produto
- Multiplique binômios com raízes quadradas
Conceitos-chave
- Propriedade do produto de raízes quadradas Se a, b são números reais não negativos, então
\(\sqrt{ab}=\sqrt{a·b}\)e\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\)
- Fórmulas especiais para multiplicar binômios e conjugados:
\[\begin{array}{ll} {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2 }&{}\\ \nonumber \end{array}\]
- O método FOIL pode ser usado para multiplicar binômios contendo radicais.


