6.1: Adicionar e subtrair polinômios
- Page ID
- 184396
Ao final desta seção, você poderá:
- Identifique polinômios, monômios, binômios e trinômios
- Determine o grau de polinômios
- Adicionar e subtrair monômios
- Adicione e subtraia polinômios
- Calcule um polinômio para um determinado valor
Antes de começar, faça este teste de prontidão.
- Simplifique:\(8x+3x\).
Se você perdeu esse problema, revise o Exercício 1.3.37. - Subtraia:\((5n+8)−(2n−1)\).
Se você perdeu esse problema, revise o Exercício 1.10.52. - Escreva em formato expandido:\(a^{5}\).
Se você perdeu esse problema, revise o Exercício 1.3.7.
Identifique polinômios, monômios, binômios e trinômios
Você aprendeu que um termo é uma constante ou o produto de uma constante e de uma ou mais variáveis. Quando é da forma\(ax^{m}\), onde\(a\) é uma constante e\(m\) é um número inteiro, é chamado de monômio. Alguns exemplos de monômio são\(8,−2x^{2},4y^{3}\),\(11z^{7}\) e.
Um monômio é um termo da forma\(ax^{m}\), onde\(a\) é uma constante e\(m\) é um número inteiro positivo.
Um monômio, ou dois ou mais monômios combinados por adição ou subtração, é um polinômio. Alguns polinômios têm nomes especiais, com base no número de termos. Um monômio é um polinômio com exatamente um termo. Um binômio tem exatamente dois termos e um trinômio tem exatamente três termos. Não há nomes especiais para polinômios com mais de três termos.
- polinômio — Um monômio, ou dois ou mais monômios combinados por adição ou subtração, é um polinômio.
- monomial — Um polinômio com exatamente um termo é chamado de monômio.
- binomial — Um polinômio com exatamente dois termos é chamado de binomial.
- trinomial — Um polinômio com exatamente três termos é chamado de trinômio.
Aqui estão alguns exemplos de polinômios.
\[\begin{array}{lllll}{\text { Polynomial }} & {b+1} &{4 y^{2}-7 y+2} & {4 x^{4}+x^{3}+8 x^{2}-9 x+1} \\ {\text { Monomial }} & {14} & {8 y^{2}} & {-9 x^{3} y^{5}} & {-13}\\ {\text { Binomial }} & {a+7}&{4 b-5} & {y^{2}-16}& {3 x^{3}-9 x^{2}} \\ {\text { Trinomial }} & {x^{2}-7 x+12} & {9 y^{2}+2 y-8} & {6 m^{4}-m^{3}+8 m}&{z^{4}+3 z^{2}-1} \end{array} \nonumber\]
Observe que todo monômio, binomial e trinomial também é um polinômio. Eles são apenas membros especiais da “família” de polinômios e, portanto, têm nomes especiais. Usamos as palavras monomial, binomial e trinomial quando nos referimos a esses polinômios especiais e apenas chamamos todos os demais polinômios.
Determine se cada polinômio é monomial, binomial, trinomial ou outro polinômio.
- \(4y^{2}−8y−6\)
- \(−5a^{4}b^{2}\)
- \(2x^{5}−5x^{3}−3x + 4\)
- \(13−5m^{3}\)
- q
- Resposta
-
\(\begin{array}{lll}&{\text { Polynomial }} & {\text { Number of terms }} & {\text { Type }} \\ {\text { (a) }} & {4 y^{2}-8 y-6} & {3} & {\text { Trinomial }} \\ {\text { (b) }} & {-5 a^{4} b^{2}} & {1} & {\text { Monomial }} \\ {\text { (c) }} & {2 x^{5}-5 x^{3}-9 x^{2}+3 x+4} & {5} & {\text { Ponomial }} \\ {\text { (d) }} & {13-5 m^{3}} & {2} & {\text { Binomial }} \\ {\text { (e) }} & {q} & {1} & {\text { Monomial }}\end{array}\)
Determine se cada polinômio é monomial, binomial, trinomial ou outro polinômio:
- 5b
- \(8 y^{3}-7 y^{2}-y-3\)
- \(-3 x^{2}-5 x+9\)
- \(81-4 a^{2}\)
- \(-5 x^{6}\)
- Resposta
-
- monomial
- polinomial
- trinomial
- binomial
- monomial
Determine se cada polinômio é monomial, binomial, trinomial ou outro polinômio:
- \(27 z^{3}-8\)
- \(12 m^{3}-5 m^{2}-2 m\)
- \(\frac{5}{6}\)
- \(8 x^{4}-7 x^{2}-6 x-5\)
- \(-n^{4}\)
- Resposta
-
- binomial
- trinomial
- monomial
- polinomial
- monomial
Determine o grau de polinômios
O grau de um polinômio e o grau de seus termos são determinados pelos expoentes da variável. Um monômio que não tem variável, apenas uma constante, é um caso especial. O grau de uma constante é 0, ou seja, ela não tem variável.
- O grau de um termo é a soma dos expoentes de suas variáveis.
- O grau de uma constante é 0.
- O grau de um polinômio é o grau mais alto de todos os seus termos.
Vamos ver como isso funciona examinando vários polinômios. Vamos fazer isso passo a passo, começando com monômios e depois progredindo para polinômios com mais termos.

Um polinômio está na forma padrão quando os termos de um polinômio são escritos em ordem decrescente de graus. Adquira o hábito de escrever primeiro o termo com o grau mais alto.
Encontre o grau dos seguintes polinômios.
- 10 anos
- \(4 x^{3}-7 x+5\)
- −15
- \(-8 b^{2}+9 b-2\)
- \(8 x y^{2}+2 y\)
- Resposta
-
- \(\begin{array}{ll} & 10y\\ \text{The exponent of y is one. } y=y^1 & \text{The degree is 1.}\end{array}\)
- \(\begin{array}{ll} & 4 x^{3}-7 x+5\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
- \(\begin{array}{ll} & -15\\ \text{The degree of a constant is 0.} & \text{The degree is 0.}\end{array}\)
- \(\begin{array}{ll} & -8 b^{2}+9 b-2\\ \text{The highest degree of all the terms is 2.} & \text{The degree is 2.}\end{array}\)
- \(\begin{array}{ll} & 8 x y^{2}+2 y\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
Encontre o grau dos seguintes polinômios:
- −15b
- \(10 z^{4}+4 z^{2}-5\)
- \(12 c^{5} d^{4}+9 c^{3} d^{9}-7\)
- \(3 x^{2} y-4 x\)
- −9
- Resposta
-
- 1
- 4
- 12
- 3
- 0
Encontre o grau dos seguintes polinômios:
- 52
- \(a^{4} b-17 a^{4}\)
- \(5 x+6 y+2 z\)
- \(3 x^{2}-5 x+7\)
- \(-a^{3}\)
- Resposta
-
- 0
- 5
- 1
- 2
- 3
Adicionar e subtrair monômios
Você aprendeu a simplificar expressões combinando termos semelhantes. Lembre-se de que termos semelhantes devem ter as mesmas variáveis com o mesmo expoente. Como monômios são termos, adicionar e subtrair monômios é o mesmo que combinar termos semelhantes. Se os monômios são como termos, nós apenas os combinamos somando ou subtraindo o coeficiente.
Adicionar:\(25 y^{2}+15 y^{2}\)
- Resposta
-
\(\begin{array}{ll} & 25 y^{2}+15 y^{2}\\ \text{Combine like terms.} & 40y^{2}\end{array}\)
Adicionar:\(12 q^{2}+9 q^{2}\)
- Resposta
-
21\(q^{2}\)
Adicionar:\(-15 c^{2}+8 c^{2}\)
- Resposta
-
\(-7 c^{2}\)
Subtraia: 16p− (−7p)
- Resposta
-
\(\begin{array}{ll} & 16p−(−7p) \\ \text{Combine like terms.} & 23p\end{array}\)
Subtraia: 8m− (−5m).
- Resposta
-
13 m
Subtrair:\(-15 z^{3}-\left(-5 z^{3}\right)\)
- Resposta
-
\(-10 z^{3}\)
Lembre-se de que termos semelhantes devem ter as mesmas variáveis com os mesmos expoentes.
Simplifique:\(c^{2}+7 d^{2}-6 c^{2}\)
- Resposta
-
\(\begin{array}{ll} & c^{2}+7 d^{2}-6 c^{2} \\ \text{Combine like terms.} & -5 c^{2}+7 d^{2} \end{array}\)
Adicionar:\(8 y^{2}+3 z^{2}-3 y^{2}\)
- Resposta
-
\(5 y^{2}+3 z^{2}\)
Adicionar:\(3 m^{2}+n^{2}-7 m^{2}\)
- Resposta
-
\(-4 m^{2}+n^{2}\)
Simplifique:\(u^{2} v+5 u^{2}-3 v^{2}\)
- Resposta
-
\ (\ begin {array} {ll} &u^ {2} v+5 u^ {2} -3 v^ {2}
\\ text {Não há termos semelhantes para combinar.} & u^ {2} v+5 u^ {2} -3 v^ {2}\ end {array}\)
Simplifique:\(m^{2} n^{2}-8 m^{2}+4 n^{2}\)
- Resposta
-
Não há termos semelhantes para combinar.
Simplifique:\(p q^{2}-6 p-5 q^{2}\)
- Resposta
-
Não há termos semelhantes para combinar.
Adicionar e subtrair polinômios
Podemos pensar em adicionar e subtrair polinômios como apenas somar e subtrair uma série de monômios. Procure termos semelhantes — aqueles com as mesmas variáveis e o mesmo expoente. A propriedade comutativa nos permite reorganizar os termos para unir termos semelhantes.
Encontre a soma:\(\left(5 y^{2}-3 y+15\right)+\left(3 y^{2}-4 y-11\right)\)
- Resposta
-
Identifique termos semelhantes. 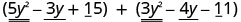
Reorganize para reunir termos semelhantes. 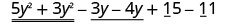
Combine termos semelhantes. 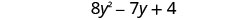
Encontre a soma:\(\left(7 x^{2}-4 x+5\right)+\left(x^{2}-7 x+3\right)\)
- Resposta
-
\(8 x^{2}-11 x+1\)
Encontre a soma:\(\left(14 y^{2}+6 y-4\right)+\left(3 y^{2}+8 y+5\right)\)
- Resposta
-
\(17 y^{2}+14 y+1\)
Descubra a diferença:\(\left(9 w^{2}-7 w+5\right)-\left(2 w^{2}-4\right)\)
- Resposta
-
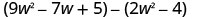
Distribua e identifique termos semelhantes. 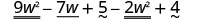
Reorganize os termos. 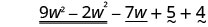
Combine termos semelhantes. 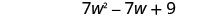
Descubra a diferença:\(\left(8 x^{2}+3 x-19\right)-\left(7 x^{2}-14\right)\)
- Resposta
-
\(15 x^{2}+3 x-5\)
Descubra a diferença:\(\left(9 b^{2}-5 b-4\right)-\left(3 b^{2}-5 b-7\right)\)
- Resposta
-
\(6 b^{2}+3\)
Subtrair:\(\left(c^{2}-4 c+7\right)\) de\(\left(7 c^{2}-5 c+3\right)\)
- Resposta
-
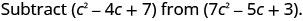
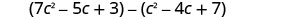
Distribua e identifique termos semelhantes. 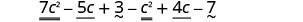
Reorganize os termos. 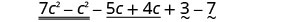
Combine termos semelhantes. 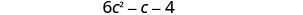
Subtrair:\(\left(5 z^{2}-6 z-2\right)\) de\(\left(7 z^{2}+6 z-4\right)\)
- Resposta
-
\(2 z^{2}+12 z-2\)
Subtrair:\(\left(x^{2}-5 x-8\right)\) de\(\left(6 x^{2}+9 x-1\right)\)
- Resposta
-
\(5 x^{2}+14 x+7\)
Encontre a soma:\(\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)\)
- Resposta
-
\(\begin{array} {ll} & {\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)} \\\text{Distribute.} & {u^{2}-6 u v+5 v^{2}+3 u^{2}+2 u v} \\ \text{Rearrange the terms, to put like terms together} & {u^{2}+3 u^{2}-6 u v+2 u v+5 v^{2}} \\ \text{Combine like terms.} & {4 u^{2}-4 u v+5 v^{2}}\end{array}\)
Encontre a soma:\(\left(3 x^{2}-4 x y+5 y^{2}\right)+\left(2 x^{2}-x y\right)\)
- Resposta
-
\(5 x^{2}-5 x y+5 y^{2}\)
Encontre a soma:\(\left(2 x^{2}-3 x y-2 y^{2}\right)+\left(5 x^{2}-3 x y\right)\)
- Resposta
-
\(7 x^{2}-6 x y-2 y^{2}\)
Descubra a diferença:\(\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)\)
- Resposta
-
\(\begin{array}{ll} & {\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)} \\ \text{Distribute.} &{p^{2}+q^{2}-p^{2}-10 p q+2 q^{2}} \\\text{Rearrange the terms, to put like terms together} & {p^{2}-p^{2}-10 p q+q^{2}+2 q^{2}} \\\text{Combine like terms.} & {-10 p q+3 q^{2}}\end{array}\)
Descubra a diferença:\(\left(a^{2}+b^{2}\right)-\left(a^{2}+5 a b-6 b^{2}\right)\)
- Resposta
-
\(-5 a b-5 b^{2}\)
Descubra a diferença:\(\left(m^{2}+n^{2}\right)-\left(m^{2}-7 m n-3 n^{2}\right)\)
- Resposta
-
\(4 n^{2}+7 m n\)
Simplifique:\(\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)\)
- Resposta
-
\(\begin{array}{ll } & {\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)} \\ \text{Distribute.} &{a^{3}-a^{2} b-a b^{2}-b^{3}+a^{2} b+a b^{2}} \\ \text{Rearrange the terms, to put like terms together} & {a^{3}-a^{2} b+a^{2} b-a b^{2}+a b^{2}-b^{3}} \\ \text{Combine like terms.} &{a^{3}-b^{3}}\end{array}\)
Simplifique:\(\left(x^{3}-x^{2} y\right)-\left(x y^{2}+y^{3}\right)+\left(x^{2} y+x y^{2}\right)\)
- Resposta
-
\(x^{3}-y^{3}\)
Simplifique:\(\left(p^{3}-p^{2} q\right)+\left(p q^{2}+q^{3}\right)-\left(p^{2} q+p q^{2}\right)\)
- Resposta
-
\(p^{3}-2 p^{2} q+q^{3}\)
Calcule um polinômio para um determinado valor
Já aprendemos como avaliar expressões. Como os polinômios são expressões, seguiremos os mesmos procedimentos para avaliar um polinômio. Substituiremos o valor fornecido pela variável e, em seguida, simplificaremos usando a ordem das operações.
Avalie\(5x^{2}−8x+4\) quando
- x=4
- x=−2
- x=0
- Resposta
-
1. x=4 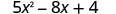

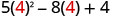
Simplifique os expoentes. 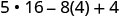
Multiplique. 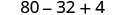
Simplifique. 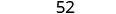
2. x=−2 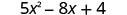

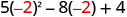
Simplifique os expoentes. 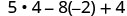
Multiplique. 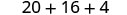
Simplifique. 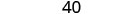
3. x=0 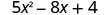

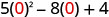
Simplifique os expoentes. 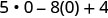
Multiplique. 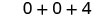
Simplifique. 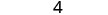
Avalie:\(3x^{2}+2x−15\) quando
- x=3
- x=−5
- x=0
- Resposta
-
- 18
- 50
- −15
Avalie:\(5z^{2}−z−4\) quando
- z=−2
- z=0
- z=2
- Resposta
-
- 18
- −4
- 14
O polinômio\(−16t^{2}+250\) fornece a altura de uma bola tt segundos após ela cair de um prédio de 250 pés de altura. Encontre a altura após t=2 segundos.
- Resposta
-
\(\begin{array}{ll } & −16t^{2}+250 \\ \text{Substitute t = 2.} & -16(2)^{2} + 250 \\ \text{Simplify }& −16\cdot 4+250 \\ \text{Simplify }& -64 + 250\\ \text{Simplify }& 186 \\& \text{After 2 seconds the height of the ball is 186 feet. } \end{array}\)
O polinômio\(−16t^{2}+250\) fornece a altura de uma bola tt segundos após ela cair de um prédio de 250 pés de altura. Encontre a altura após t=0 segundos.
- Resposta
-
250
O polinômio\(−16t^{2}+250\) fornece a altura de uma bola tt segundos depois que ela caiu de um prédio de 250 pés de altura. Encontre a altura após t=3 segundos.
- Resposta
-
106
O polinômio\(6x^{2}+15xy\) fornece o custo, em dólares, de produzir um recipiente retangular cuja parte superior e inferior são quadrados com lado x pés e lados de altura y pés. Encontre o custo de produzir uma caixa com x = 4 pés e y = 6 y = 6 pés.
- Resposta
-
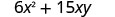
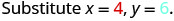
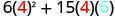
Simplifique. 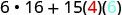
Simplifique. 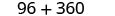
Simplifique. 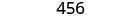
O custo de produção da caixa é de $456.
O polinômio\(6x^{2}+15xy\) fornece o custo, em dólares, de produzir um recipiente retangular cuja parte superior e inferior são quadrados com lado x pés e lados de altura y pés. Encontre o custo de produzir uma caixa com x = 6 pés e y = 4 pés.
- Resposta
-
$576
O polinômio\(6x^{2}+15xy\) fornece o custo, em dólares, de produzir um recipiente retangular cuja parte superior e inferior são quadrados com lado x pés e lados de altura y pés. Encontre o custo de produzir uma caixa com x = 5 pés e y = 8 pés.
- Resposta
-
$750
Conceitos-chave
- Monômios
- Um monômio é um termo da forma\(ax^{m}\), onde aa é uma constante e mm é um número inteiro
- Um monômio é um termo da forma\(ax^{m}\), onde aa é uma constante e mm é um número inteiro
- Polinômios
- polinômio — Um monômio, ou dois ou mais monômios combinados por adição ou subtração, é um polinômio.
- monomial — Um polinômio com exatamente um termo é chamado de monômio.
- binomial — Um polinômio com exatamente dois termos é chamado de binomial.
- trinomial — Um polinômio com exatamente três termos é chamado de trinômio.
- Grau de um polinômio
- O grau de um termo é a soma dos expoentes de suas variáveis.
- O grau de uma constante é 0.
- O grau de um polinômio é o grau mais alto de todos os seus termos.
Glossário
- binomial
- Um binômio é um polinômio com exatamente dois termos.
- grau de uma constante
- O grau de qualquer constante é 0.
- grau de um polinômio
- O grau de um polinômio é o grau mais alto de todos os seus termos.
- grau de um termo
- O grau de um termo é o expoente de sua variável.
- monomial
- Um monômio é um termo da forma\(ax^m\), onde a é uma constante e m é um número inteiro; um monômio tem exatamente um termo.
- polinomial
- Um polinômio é um monômio, ou dois ou mais monômios combinados por adição ou subtração.
- formulário padrão
- Um polinômio está na forma padrão quando os termos de um polinômio são escritos em ordem decrescente de graus.
- trinomial
- Um trinômio é um polinômio com exatamente três termos.


